FUNDAMENTALS OF THERMAL ANALYSIS AND DIFFERENTIAL SCANNING CALORIMETRY

Introduction • All old and modern methods of thermal analysis require precise and repeatable

2. 1. Thermal expansion • The source for thermal expansion is an asymmetry in

2. 1. Thermal expansion As was schematically marked at large distances L of the

2. 1. Thermal expansion Fig. 2. 2. Schematic presentation of the deviation of L

2. 1. Thermal expansion Anisotropy of the volume expansion In case of amorphous and

2. 1. Thermal expansion Fig. 2. 3. Anisotropic change of the crystal lattice dimensions

2. 1. Thermal expansion Summarising: Linear coefficient of thermal expansion a is reversibly proportional

2. 2. Thermal conductivity Determination of thermal conductivity requires investigation of the space and

2. 2. Thermal conductivity Fig. 2. 4. Basic definitions concerning temperature stress field and

2. 3. Temperature scales The basic scale of temperature accepted in science is kelvin

2. 3. Temperature scales The ITS 1990 scale starts from the triple point of

2. 4. Thermometers and thermometry Frequently used types of thermometers are : • Liquid

2. 4. Thermometers and thermometry The proper temperature determination needs: 1. Direct contact with

2. 4. Thermometers and thermometry To have high precision temperature measurements the liquid in

2. 4. Thermometers and thermometry Other type of thermometers 1. Quartz thermometer – bases

Slides: 24

Download presentation

FUNDAMENTALS OF THERMAL ANALYSIS AND DIFFERENTIAL SCANNING CALORIMETRY Application in Materials Science Investigations Analiza cieplna i kalorymetria różnicowa w badaniach materiałów Tomasz Czeppe Lecture 2 (3). Thermal properties of materials, temperature scales and thermometry

Introduction • All old and modern methods of thermal analysis require precise and repeatable temperature measurements and for this thermometers had to be invented. Before short discussion concerning thermometry two basic properties related to precision of the temperature measurements, thermal expansion and thermal conductivity are discussed. • Thermal conductivity is the basic event for all thermal analysis methods and phase transitions, thermal expansion is also the subject of dilatometry and thermo-mechanical analysis TMA.

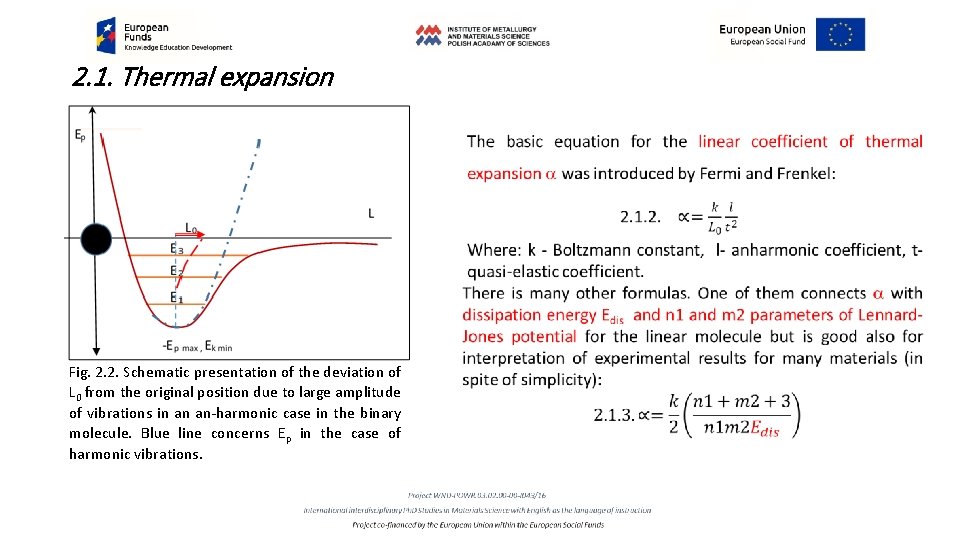
2. 1. Thermal expansion • The source for thermal expansion is an asymmetry in the atoms thermal oscillations that is anharmonic part in the oscillations. As we must remember, on the base of quantum physics the energy of atomic thermal oscillations in the solid state are quantified revealing both character of the elastic waves and particles named phonons. • To understand the nature of thermal expansion in the solid state, at first it is enough to analyse dependence of the potential Ep and kinetic Ek components of the total energy Et from the distance L in case of the simple two atomic, linear molecule (Fig. 2. 1).

2. 1. Thermal expansion As was schematically marked at large distances L of the atoms the interaction is very week so the force F is 0 and the Ep very small and constant. And some smaller distance the interaction starts to be effective generating the attracting force F. If the distance L further decreases the repulsive forces are increasing what generates the equilibrium distance L 0, at which F=0 and the potential Fig. 2. 1. Schematic presentation of the dependence of Ep and F from the atoms distance L in the binary molecule. energy Ep has a minimum. Further decreasing the distance L cases strong increase in the repulsion forces. As is clear there is strong asymmetry in attracting and repulsive interaction between the atoms in a molecule.

2. 1. Thermal expansion •

2. 1. Thermal expansion Fig. 2. 2. Schematic presentation of the deviation of L 0 from the original position due to large amplitude of vibrations in an an-harmonic case in the binary molecule. Blue line concerns Ep in the case of harmonic vibrations.

2. 1. Thermal expansion

2. 1. Thermal expansion Anisotropy of the volume expansion In case of amorphous and polycrystalline materials the isotropy of thermal expansion may be assumed. In the case of monocrystals, in the case of crystal lattice not belonging to the cubic symmetry, the volume expansion is not isotropic. In this case heating of the crystal results in anisotropic dimensional increase which must be represented by the tensor of deformation Eij. For the temperature increase by DT the tensor components proportionally change in the chosen direction : 2. 1. 6. eij = aij. DT Both eij and aij are symmetrical tensors of the second order. If we transform the tensor to the main axis of the crystal lattice, only diagonal components are different from 0.

2. 1. Thermal expansion Fig. 2. 3. Anisotropic change of the crystal lattice dimensions by the tensor of thermal expansion in main axis system in 2 D. Anisotropic change of the crystal lattice dimensions in the 2 D main axis system is presented in Fig. XX. For the 3 D system the volume coefficient of thermal expansion will have the form: 2. 1. 7. b = a 11 + a 22 + a 33

2. 1. Thermal expansion Summarising: Linear coefficient of thermal expansion a is reversibly proportional to dissipation energy; Volume coefficient of thermal expansion b is proportional to Cv and may be summarized from the components: lattice, electron and other; 6 n In case of monocrystals: for the cubic crystals : a 11 = a 22 = a 33 = a and b = 3 a for the hexagonal and trigonal crystals: a 2 isotropic expansion; a 11 = a 22 = a 1, a 33 = a 2 and b = 2 a 1+ a 2 a 1 anisotropic expansion (contraction) in one direction; for rhombohedral crystals: b = a 11 + a 22 + a 33 anisotropic expansion in 3 D In all this system the ellipsoid axis are parallel to the crystallographic axis, but for monoclinic and triclinic crystals things are more complicated.

2. 2. Thermal conductivity Determination of thermal conductivity requires investigation of the space and time dependence of temperature T = f(x, y, z, t), that is thermal field. While the temperature reveals time dependence, d. T/dt=0, we have stationary thermal field, opposite, while d. T/dt=f(t) the field is nonstationary. Interconnection of all the points revealing the same temperature T in (x, y, z) space defines an isothermal surface. Increase of the temperature in the direction perpendicular to the isothermal surface changes character from the scalar quantity of T to the vector quantity of the stress of thermal field W: 2. 1. 8 W = grad T= (d. T/dx + d. T/dy + d. T/dz) The amount of heat passing in a unit of time t through the unit area of the isothermal surface S in the direction x: 2. 1. 9 q = (d. T/dt)S-1. x is named density of heat flux (vector character) (Fig. 2. 4)

2. 2. Thermal conductivity Fig. 2. 4. Basic definitions concerning temperature stress field and heat flux.

2. 2. Thermal conductivity

2. 3. Temperature scales The basic scale of temperature accepted in science is kelvin scale. It represents the absolute temperature scale basing on gas thermodynamics lows with two main points: absolute 0 and the triple point of water arbitrary placed at 273. 16 K. This range defines also the measure of 1 K. This is such named primary temperature scale, however in the experimental practice the highest precision in temperature determination cannot be achieved. So, there is need for the secondary temperature scales. This scale is named International Temperature Scale 1990 (ITS 1990). It bases on the 14 temperature points for thermometers scaling. The points are triple, melting or freezing points of gasses, water and metallic elements at constant pressure P = 101, 325 Pa at standard atmosphere.

2. 3. Temperature scales The ITS 1990 scale starts from the triple point of H 2 at equilibrium (13, 8033 K - 259, 3467 o. C), the low temperature range limit is at the triple point of water at 273, 16 K - 0, 02 o. C, and this gives constant difference between the C and K scales, high temperature range starts from Ga melting point at 302. 9146 K - 29. 7646 o. C and finishes at the freezing point of Cu (1357. 77 K - 1084. 62 o. C). Why the freezing, that is crystallization temperatures were chosen for thermometers calibration will be clear when we see thermal curves including melting and crystallization of pure metals. To use temperature scale thermometer had to be invented. The temperature ranges covered by the different (basic) thermometers are as follows: 0. 65 – 5 K vapor-pressure relationships for 3 He and 4 He; 3. 0 – 24. 5561 K helium gas thermometer; 13. 8033 – 1234. 93 K platinum resistance thermometer; Above 1234. 93 monochromatic radiation pyrometer.

2. 4. Thermometers and thermometry Frequently used types of thermometers are : • Liquid in glass thermometers • Resistance thermometers and thermocouples 2. 4. 1. Liquid in glass thermometers Till the development of electronic resistance thermometers and semiconductor thermometers a Hg post in thin glass or quartz capillary was the most useful and widely applied thermometer. However, its development, fundamental for the development of sciences, was not easy, due to the lack of the repeatability and precision of measurements. (The same concerned also barometers and similar measuring apparats. ) This was caused by the lack of the technology of the glass capillary production. The temperature range of application is 240 -800 K. The common precision is ± 0. 001 K, but may be higher.

2. 4. Thermometers and thermometry The proper temperature determination needs: 1. Direct contact with measured object Tt 2. Time enough for thermal equilibrium 3. Corrections for heat flow Ts The source of errors could be: • Lack of the stable volume of the bulb. This may result from thermal history of thermometer or from the hysteresis of the volume, • Thermometer lag, • Pressure effect, • Immersion effect (Fig. 2. 5) n Err = kn(Tt – T 0) n- Hg column above the bath (e. g-84 K) Ts - bath temperature Tt – temperature read from therm. (e. g -366. 0 K) (eg. 273) T 0 – thermometer scale starting temperature k- differential of glass-Hg expansivity k ~ 1. 6. 10 -4 K-1 Ts = 366 +1. 6. 10 -4. 84(366 -273) = 366. 0 + 1. 25=367. 25

2. 4. Thermometers and thermometry To have high precision temperature measurements the liquid in glass thermometers must be calibrated for one temperature from time to time. 1. The hysteresis results from the difference in time required for the achieving the final volume of the bulb in heating (short) and in cooling. The last one may be very long. 2. Thermometer lag results from thermal conductivity of thermometer materials, that is proper time is required for heat to enter and equilibrated the internal part of thermometer. 3. Pressure differences in the bulb results in differences in reading temperature. They may result from the different position of thermometer. 4. The most important errors results from the immersion problems. Some thermometers have marks informing how deep must be immersion in the liquid.

2. 4. Thermometers and thermometry Other type of thermometers 1. Quartz thermometer – bases on the measurements of frequency of an oscillator controlled by the quartz crystal, temperature dependent. Temperature range 200 -500 K, resolution 10 -4 K; 2. Pyrometer – measures light intensity of a given, narrow frequency range; 3. Bimetallic thermometer – not very precise; 4. Vapour pressure thermometer, measures pressure under a liquid being in contact with the investigated system. Especially useful at low temperatures; 5. Gas thermometer- uses Boil-Marriott gas low PV=n. RT; 6. Noise thermometer- measures random noise of electrons in conductors;