Fundamental Concept ENT 485 FEA Dr Rakhmad Arief







![Stress and Equilibrium n The load Pi = [Px, Py, Pz]T The six independent Stress and Equilibrium n The load Pi = [Px, Py, Pz]T The six independent](https://slidetodoc.com/presentation_image_h/11a15f23d2b47c044a86d6252c33cab9/image-8.jpg)















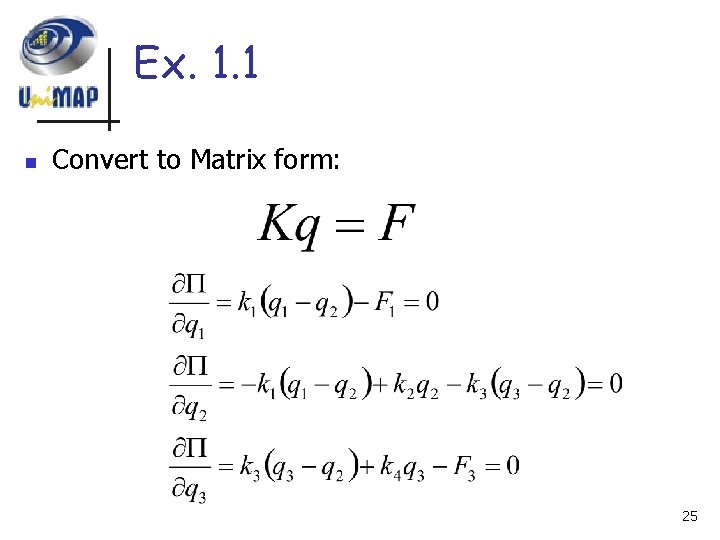


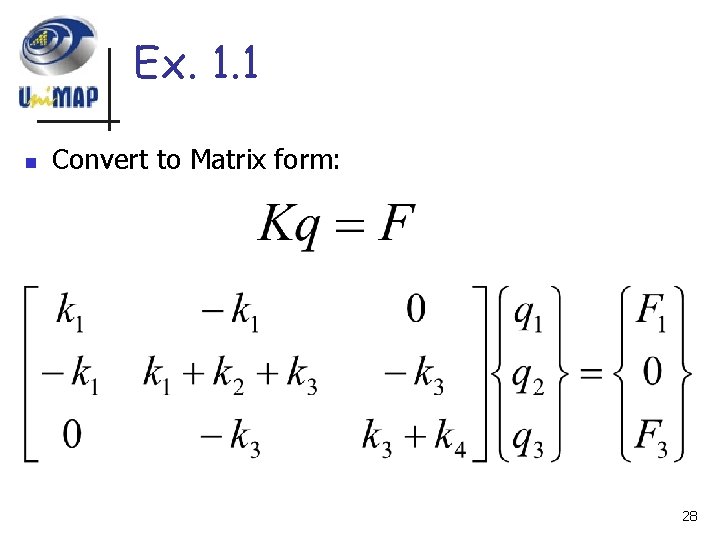










- Slides: 42

Fundamental Concept ENT 485 FEA Dr. Rakhmad Arief Siregar 1

Fundamental Concepts n n n Introduction FEA (Finite Element Analysis) or in other names FEM (Finite Element Method) has become a powerful tool for the numerical solution of a wide range of engineering problems Application of FEA: Deformation and stress analysis of automotive, aircraft, building, and bridge structural Field analysis of heat flux, fluid flow, magnetic flux seepage and other flow problems 2

Fundamental Concepts Introduction n With the advances in computer technology and CAD systems, complex problems can be modeled relative ease. n Several alternative configurations can be tested on a computer before the first prototype is built 3

Fundamental Concepts The concept of FEA n In this method, a complex region defining a continuum is discretized into simple geometric shapes called finite elements n The material properties, and the governing relationships are considered over these elements and expressed in terms of unknown values at element corners n An assembly process, considering the loading and constraints, results in a set of equations. 4

Historical Background n n n Basic ideas of FEM originated from Aircraft structural analysis 1941, Hrenikoff frame work method 1943, Courant’s torsion problem 1956, Turner, et al. stiffness matrices for truss, beam and other elements 1960, Clough the term finite element was coined. 5

Historical Background n n Books 1955, Argyris energy trorems and matrix methods 1967, Zienkiewics first book of FEM 1972, Oden nonlinear continua 6

Stress and Equilibrium n n n A three-dimensional body occupying a volume V and having a surface S. The boundary, distributed force per unit T is applied. The deformation u = [u, v, w]T The distributed force f = [fx, fy, fz]T The surface traction T = [Tx, Ty, Tz]T 7
![Stress and Equilibrium n The load Pi Px Py PzT The six independent Stress and Equilibrium n The load Pi = [Px, Py, Pz]T The six independent](https://slidetodoc.com/presentation_image_h/11a15f23d2b47c044a86d6252c33cab9/image-8.jpg)
Stress and Equilibrium n The load Pi = [Px, Py, Pz]T The six independent components are: n The equilibrium equations n 8

Boundary Conditions n Consideration of equilibrium along the three axes direction: 9

Strain-Displacement Relations n The strain in vector n Strain-displacement 10

Stress-Strain Relation n For linear elastic materials, the stress-strain relations come from the generalize Hooke’s law 11

Stress-Strain Relation n Shear modulus (or modulus of rigidity) n From Hooke’s relationships 12

Stress-Strain Relation n Substituting for ( y + z), we get the inverse relations 13

Special Cases n One dimension Stress-strain relations 14

Special Cases n Two dimensions n Plane Stress 15

Special Cases n Two dimensions n Plane Strain 16

Temperature Effects n If the temperature rise T(x, y, z) then the associated deformation can be considered. 0 = [ T, T, 0, 0, 0] = D ( - 0) Plane stress: n Plane strain: n 17

Potential Energy n The total potential energy : Strain energy Work potential 18

Potential Energy n Total strain energy (U): n The work potential (WP): 19

Potential Energy n Total Potential Energy for general elastic body: 20

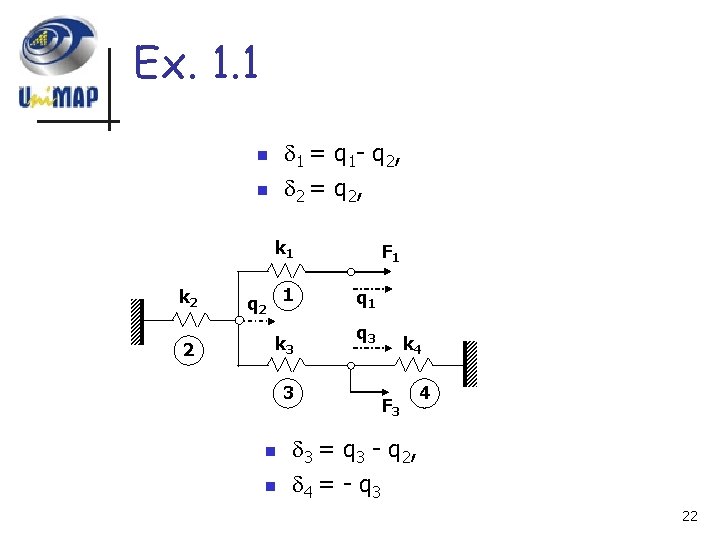
Ex. 1. 1 n n Figure below shows a system of springs. The total potential energy is given by where 1, 2 , 3 , and 4 are extension of four springs. k 1 k 2 q 2 1 2 k 3 3 F 1 q 3 k 4 F 3 4 21

Ex. 1. 1 1 = q 1 - q 2 , 2 = q 2 , n n k 1 k 2 q 2 1 2 k 3 3 n n F 1 q 3 k 4 F 3 4 3 = q 3 - q 2 , 4 = - q 3 22

Ex. 1. 1 n By substituting 23

Ex. 1. 1 n Minimizing with respect to q 1, q 2 and q 3 24
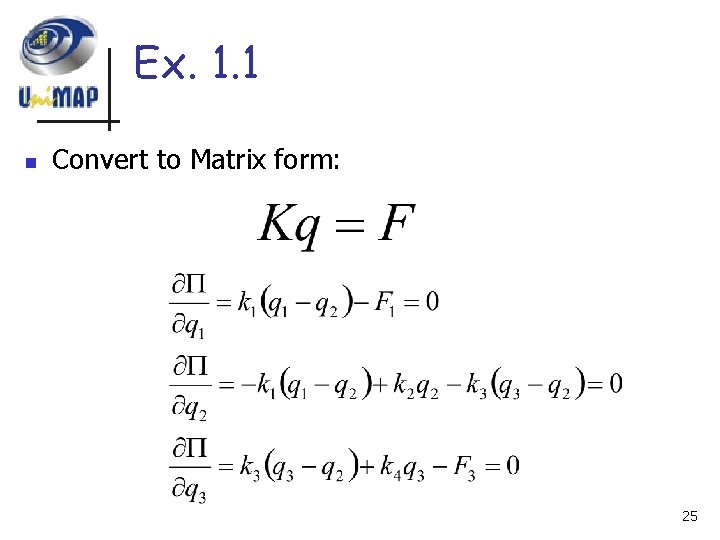
Ex. 1. 1 n Convert to Matrix form: 25

Ex. 1. 1. . . = 26

Ex. 1. 1 27
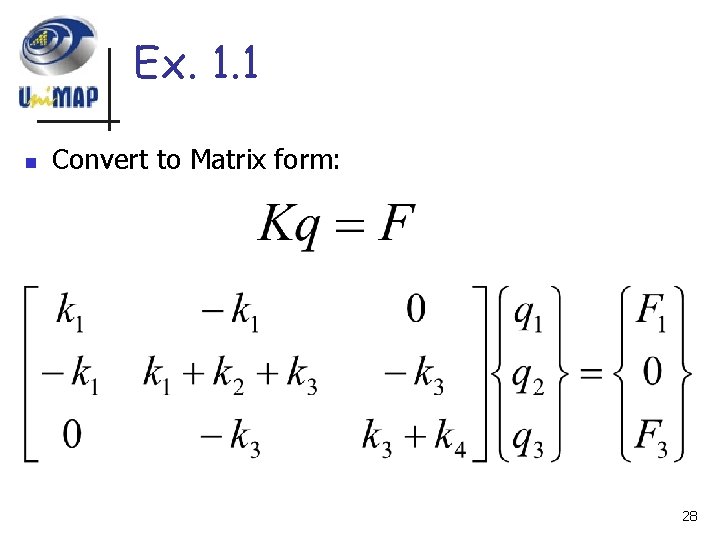
Ex. 1. 1 n Convert to Matrix form: 28

Ex. 1. 1 n The equilibrium equations of the system by considering the equilibrium of each separate node k 1 1 = F 1 k 1 1 k 2 2 – k 1 1 – k 3 3 = 0 k 2 2 2 k 3 3 k 3 3 – k 4 4 = F 3 k 3 3 3 k 4 4 F 3 29

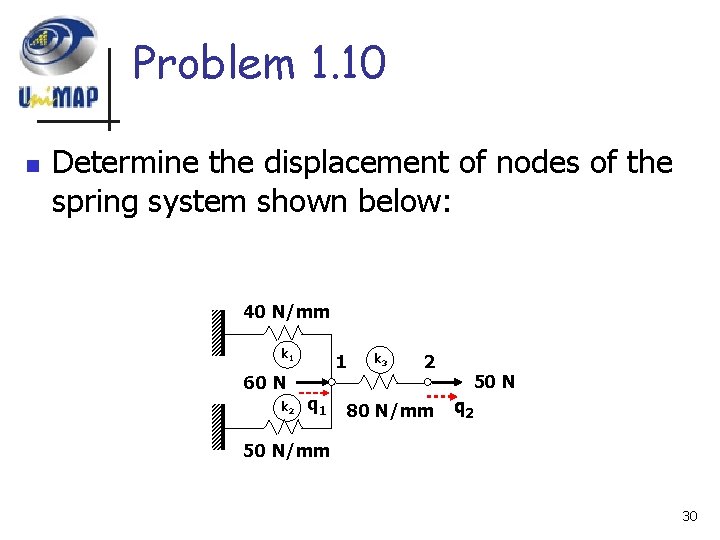
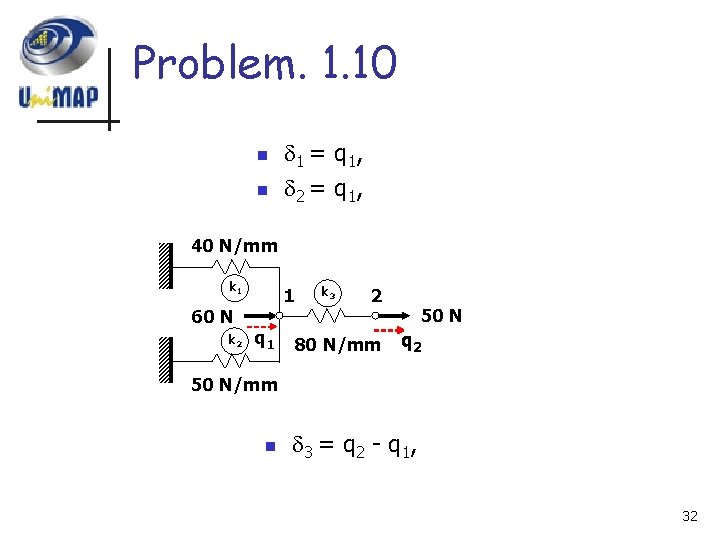
Problem 1. 10 n Determine the displacement of nodes of the spring system shown below: 40 N/mm k 1 60 N k 2 1 q 1 k 3 2 80 N/mm 50 N q 2 50 N/mm 30

Problem. 1. 10 n n Figure below shows a system of springs. The total potential energy is given by where 1, 2 , and 3 are extension of four springs. 40 N/mm k 1 60 N k 2 1 q 1 50 N/mm k 3 2 80 N/mm 50 N q 2 31

Problem. 1. 10 n n 1 = q 1 , 2 = q 1 , 40 N/mm k 1 60 N k 2 1 q 1 k 3 2 80 N/mm 50 N q 2 50 N/mm n 3 = q 2 - q 1 , 32

Problem. 1. 10 n By substituting 33

Problem 1. 10 n Minimizing with respect to q 1, and q 2 34

Problem 1. 10 35

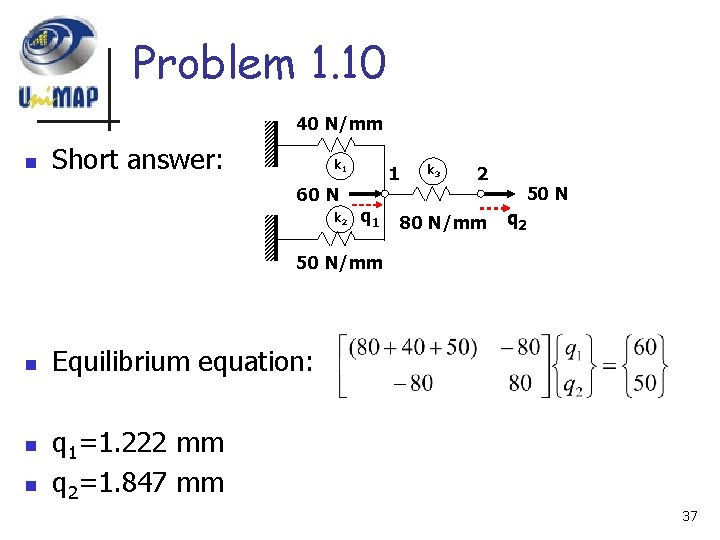
Problem 1. 10 n Convert to Matrix form: 36

Problem 1. 10 40 N/mm n Short answer: k 1 60 N k 2 1 q 1 k 3 2 80 N/mm 50 N q 2 50 N/mm n n n Equilibrium equation: q 1=1. 222 mm q 2=1. 847 mm 37

Rayleigh-Ritz Method n n For continua, total potential energy are used for finding approximate solution Displacement field can be constructed by using The Rayleigh-Ritz method 38

Rayleigh-Ritz Method n An assumed displacement field: 39

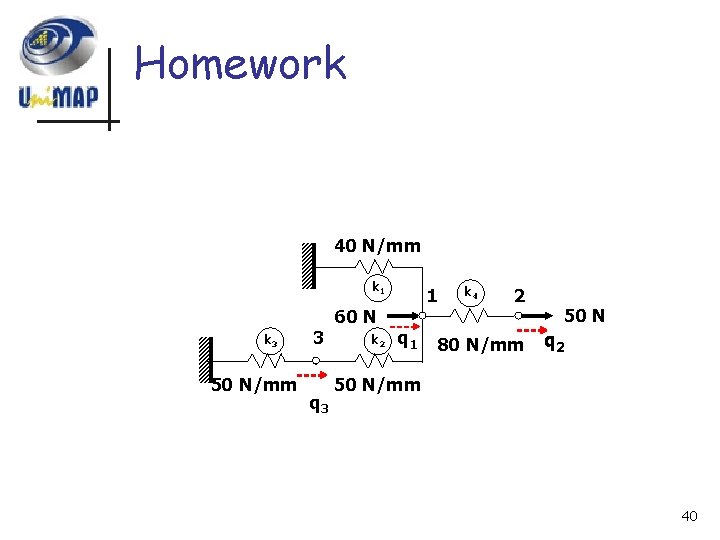
Homework 40 N/mm k 1 k 3 50 N/mm 3 q 3 60 N k 2 1 q 1 k 4 2 80 N/mm 50 N q 2 50 N/mm 40

FYI - Greek Alphabetn n n Alpha Beta Gamma Delta Epsilon Zeta Eta Theta Iota Kappa Lambda Mu n n n Nu Xi Omicron Pi Rho Sigma Tau Upsilon Phi Rho Psi Omega 41

n End 42
 Ig5a 485 통신 예제
Ig5a 485 통신 예제 Ley 26 485
Ley 26 485 Arief isti pramusinta
Arief isti pramusinta Dokter paru paru terdekat
Dokter paru paru terdekat Lokasi infark berdasarkan ekg
Lokasi infark berdasarkan ekg Krisis hipertensi
Krisis hipertensi Dr budi arief waskito
Dr budi arief waskito Prof. dr. arief s. rachmat
Prof. dr. arief s. rachmat Bakso arief trunojoyo bandung
Bakso arief trunojoyo bandung Arief yuwono
Arief yuwono Arief wibowo fkm unair
Arief wibowo fkm unair Difference between fea and fem
Difference between fea and fem What is fea
What is fea Fea
Fea Fpix
Fpix Fea framework
Fea framework Internal design review
Internal design review Ucsd immunology course
Ucsd immunology course Maya fea
Maya fea La niña negrita y el conejo blanco
La niña negrita y el conejo blanco Fem applications
Fem applications Rimas del poema la higuera
Rimas del poema la higuera Data reference model
Data reference model Alva myrda
Alva myrda The fundamental concept of economics is
The fundamental concept of economics is What is the fundamental concept behind premium marketing?
What is the fundamental concept behind premium marketing? Discounting concept in managerial economics
Discounting concept in managerial economics What is the fundamental concept of the gmdss?
What is the fundamental concept of the gmdss? What is the similarities of actual self and ideal self
What is the similarities of actual self and ideal self Contoh selling concept
Contoh selling concept Dr max klein ent
Dr max klein ent Fsjes el jadida
Fsjes el jadida Mark draper ent
Mark draper ent Ent supelec
Ent supelec 163 ent
163 ent Swedish ent
Swedish ent Dr abdul hadi ent specialist
Dr abdul hadi ent specialist Lesson 5: electrical nonmetallic tubing (ent)
Lesson 5: electrical nonmetallic tubing (ent) Ent collège claude cornac
Ent collège claude cornac 143 ent
143 ent Ent marne mon bureau numérique
Ent marne mon bureau numérique Ent uh1
Ent uh1 Hennebert sign
Hennebert sign


































































