Forty Years of Corner Polyhedra Two Types of

Forty Years of Corner Polyhedra

Two Types of I. P. • All Variables (x, t) and data (B, N) integer. Example: Traveling Salesman • Some Variables (x, t) Integer, some continuous, data continuous. Example: Scheduling, Economies of scale. • Corner Polyhedra relevant to both

Corner Polyhedra Origins Stock Cutting • Computing Lots of Knapsacks • Periodicity observed • Gomory-Gilmore 1966 "The Theory and Computation of Knapsack Functions“

Equations

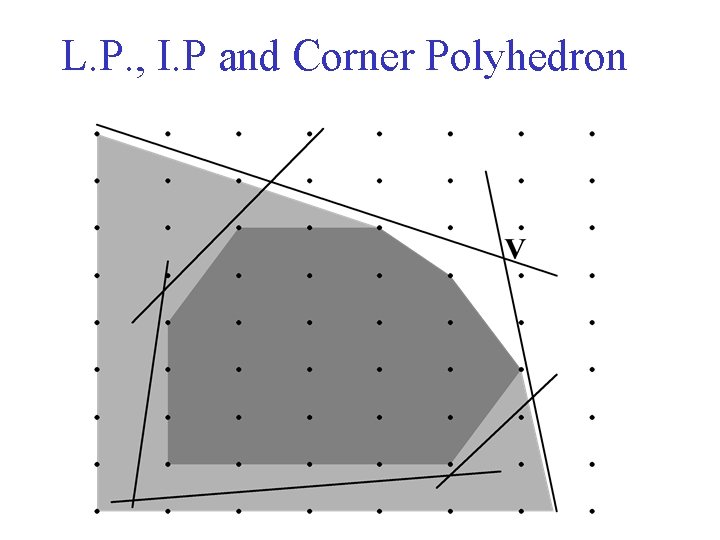
L. P. , I. P and Corner Polyhedron

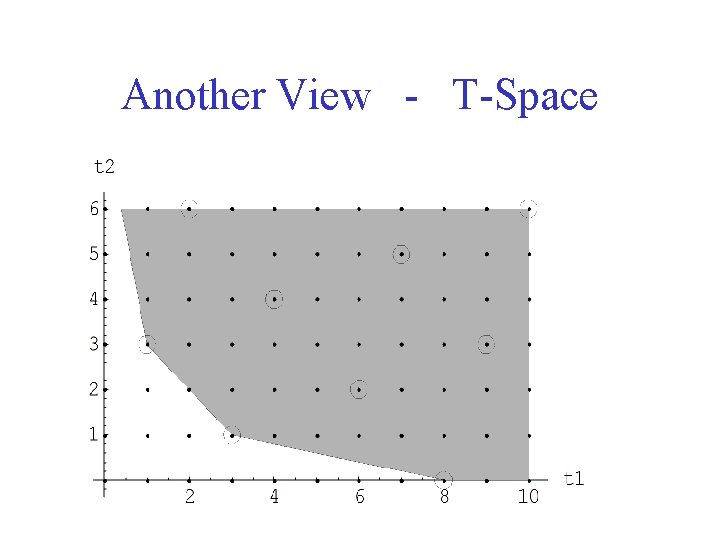
Another View - T-Space

Cutting Planes for Corner Polyhedra are Cutting Planes for General I. P.

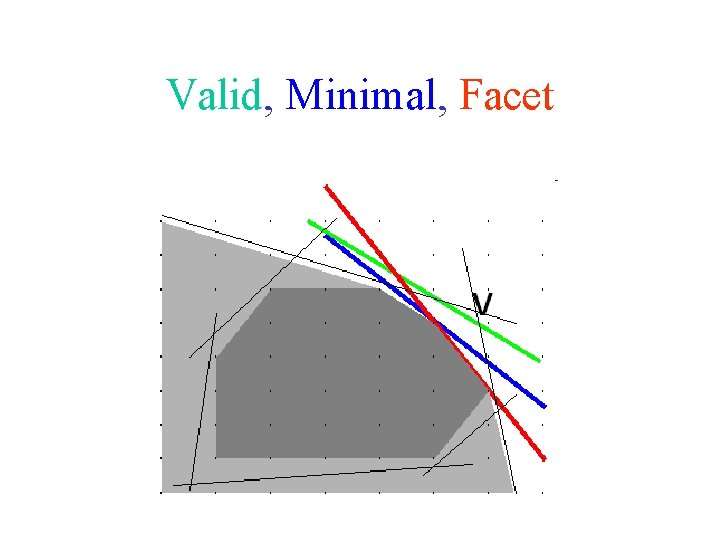
Valid, Minimal, Facet

T-Space View

Cutting Planes for Corner Polyhedra

Structure Theorem- 1969

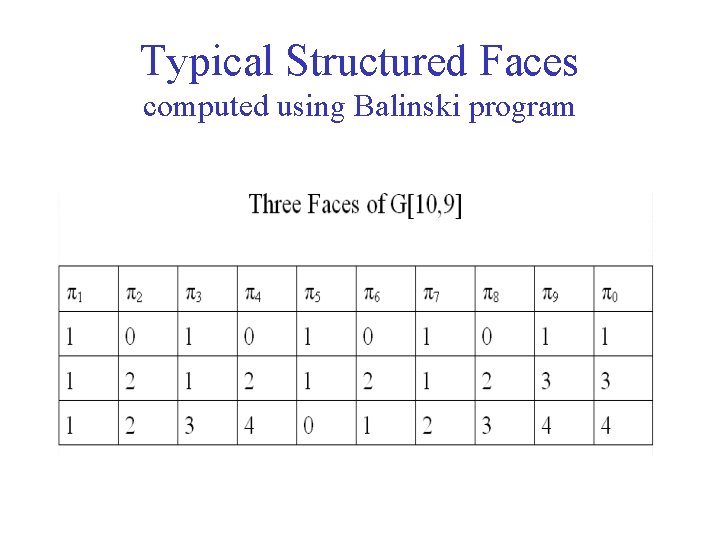
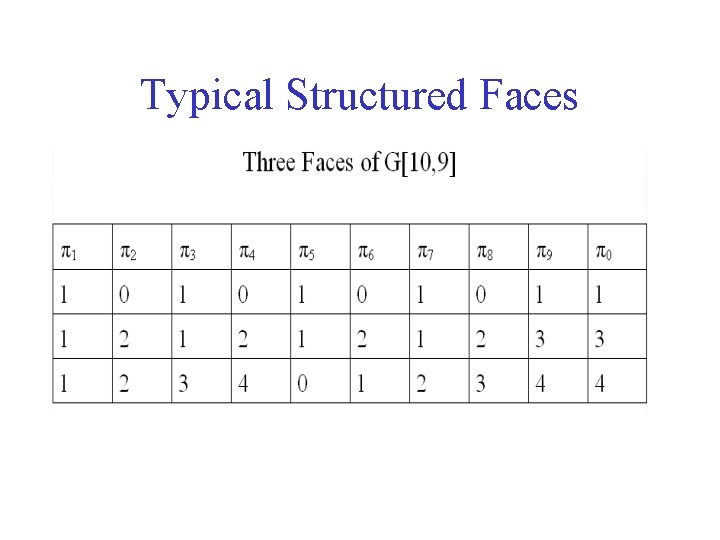
Typical Structured Faces computed using Balinski program

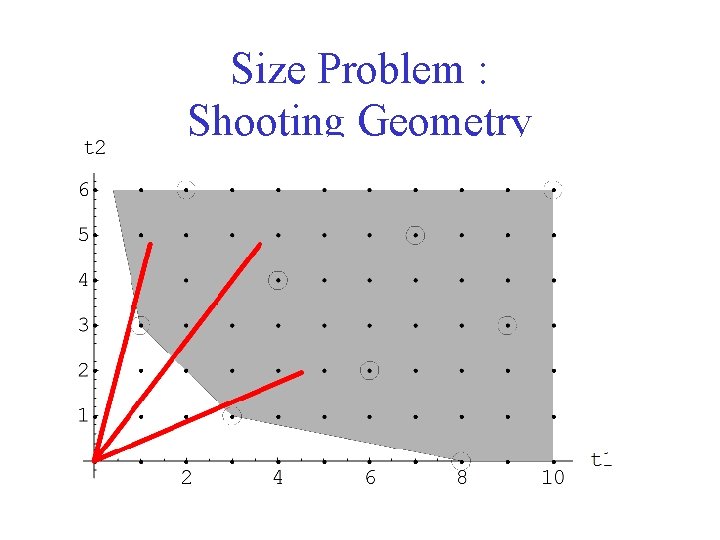
Size Problem : Shooting Geometry

Size Problem -Shooting Theorem

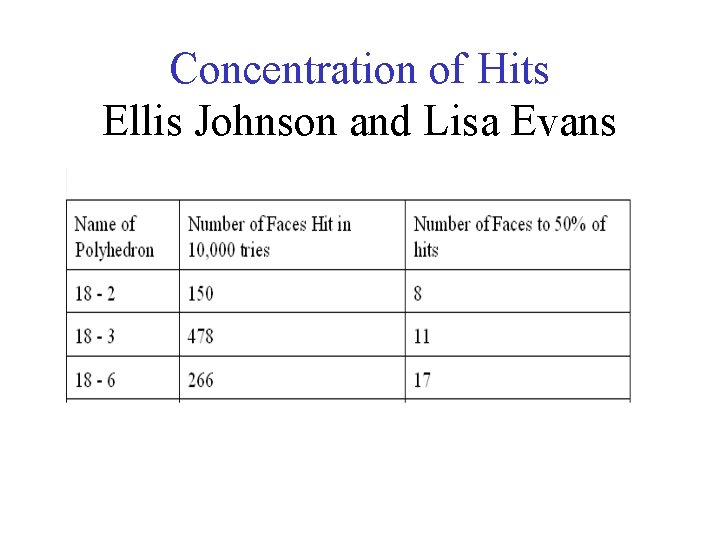
Concentration of Hits Ellis Johnson and Lisa Evans

Much More to be Learned

Comparing Integer Programs and Corner Polyhedron • General Integer Programs – Complex, no obvious structure • Corner Polyhedra – Highly structured, but complexity increases rapidly with group size. • Next Step: Making this supply of cutting planes available for non-integer data and continuous variables. Gomory-Johnson 1970

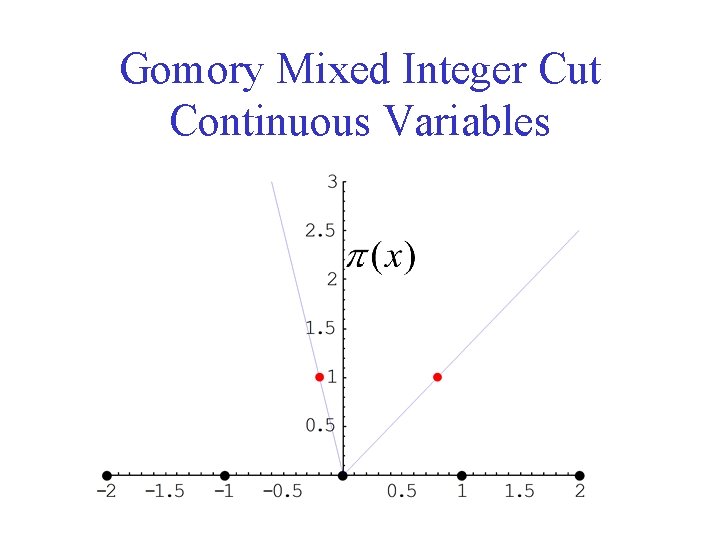
Cutting Planes for Type Two • • Example: Gomory Mixed Integer Cut Variables ti Integer Variables t+, t- Non-Integer Valid subadditive function

Typical Structured Faces

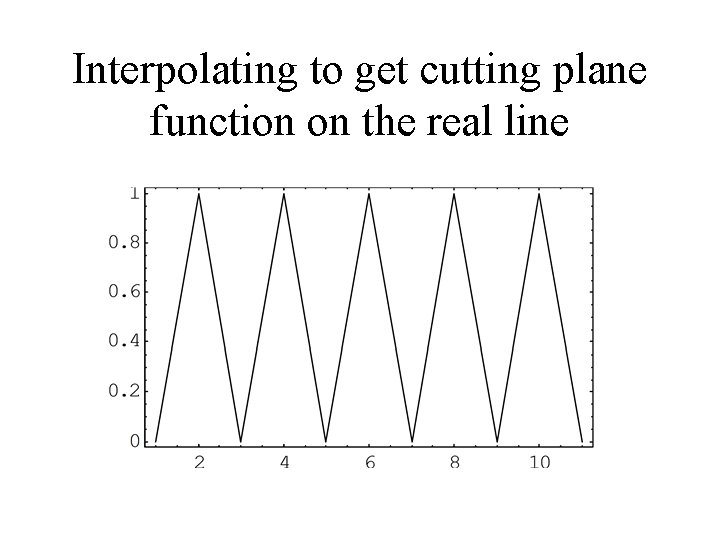
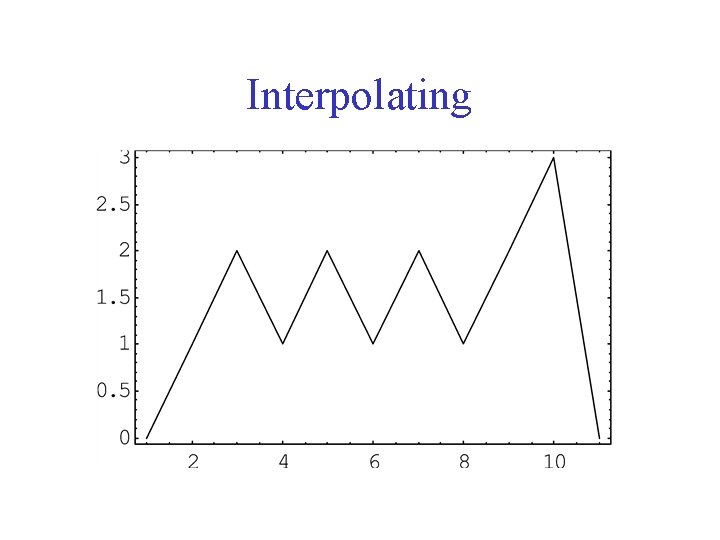
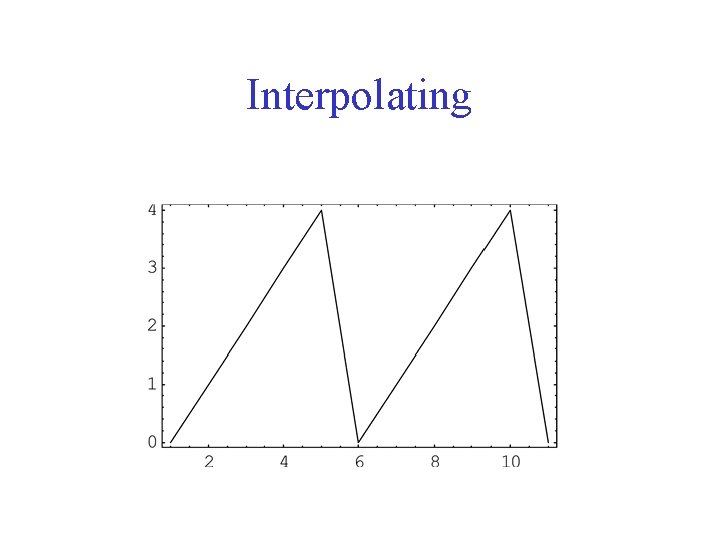
Interpolating to get cutting plane function on the real line

Interpolating

Interpolating

Gomory-Johnson Theorem

Integer Variables Example 2

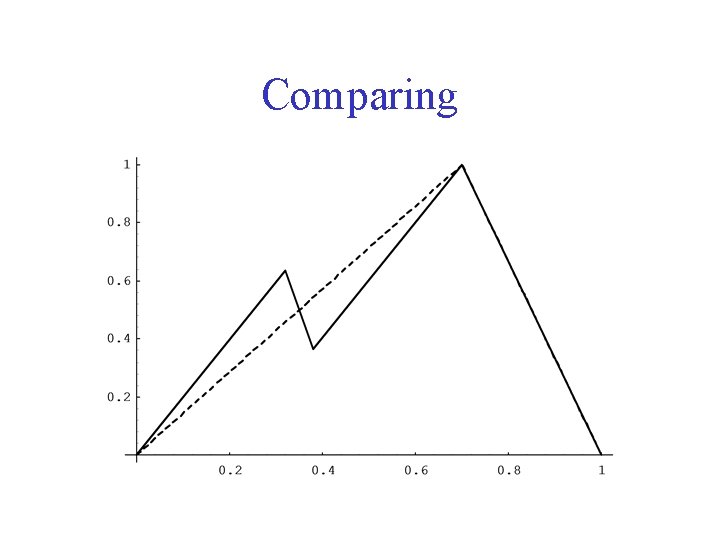
Integer Based Cuts • A great variety of cutting planes generated from Integer Theory • But more developed cutting planes weaker than the Gomory Mixed Integer Cut for their continuous variables

Comparing

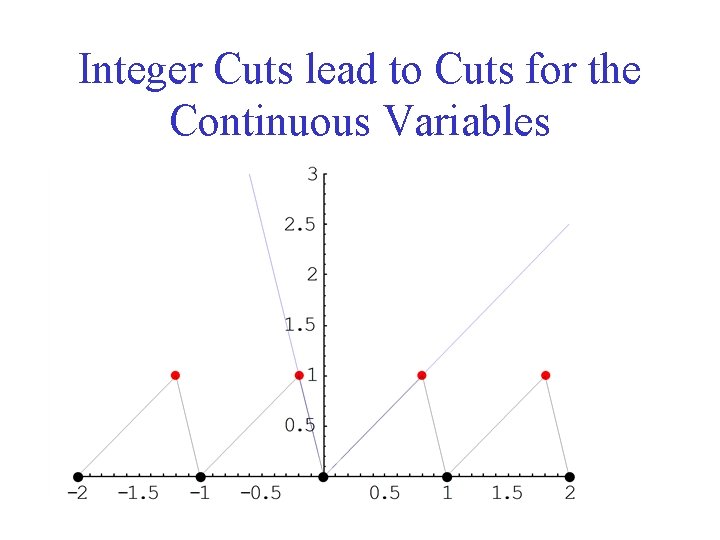
Integer Cuts lead to Cuts for the Continuous Variables

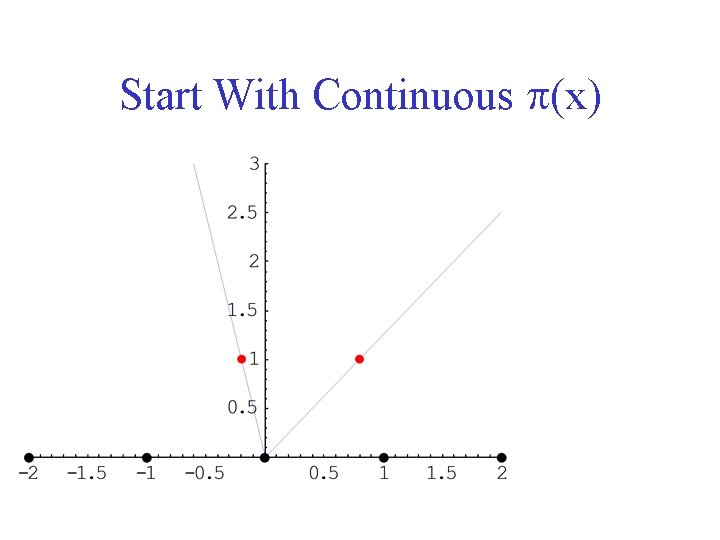
Gomory Mixed Integer Cut Continuous Variables

New Direction • Reverse the present Direction • Create facets for continous variables • Turn them into facets for the integer problem • Montreal January 2007, Georgia Tech August 2007

Start With Continuous p(x)

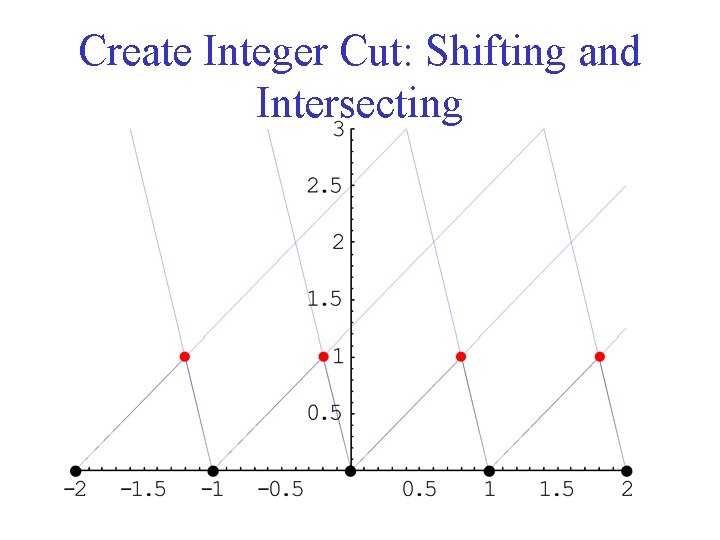
Create Integer Cut: Shifting and Intersecting

Shifting and Intersecting

One Dimension Continuous Problem

Direction • Move on to More Dimensions

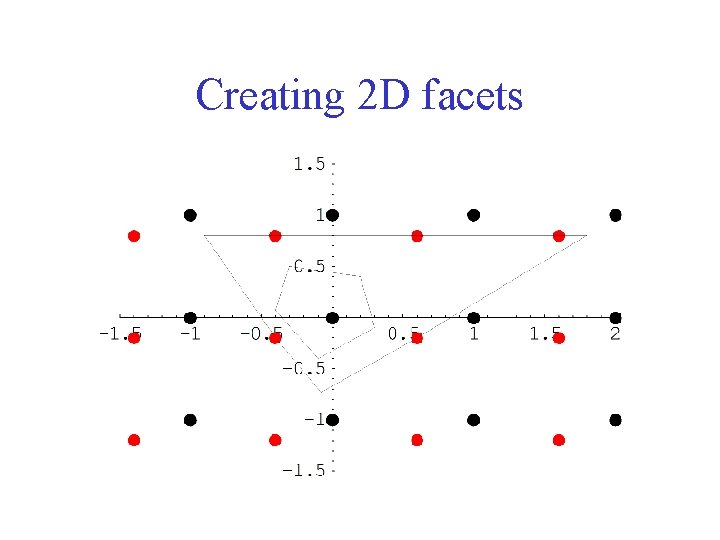
Helper Theorem If is a facet of the continous problem, then (kv)=k (v). This will enable us to create 2 -dimensional facets for the continuous problem.

Creating 2 D facets

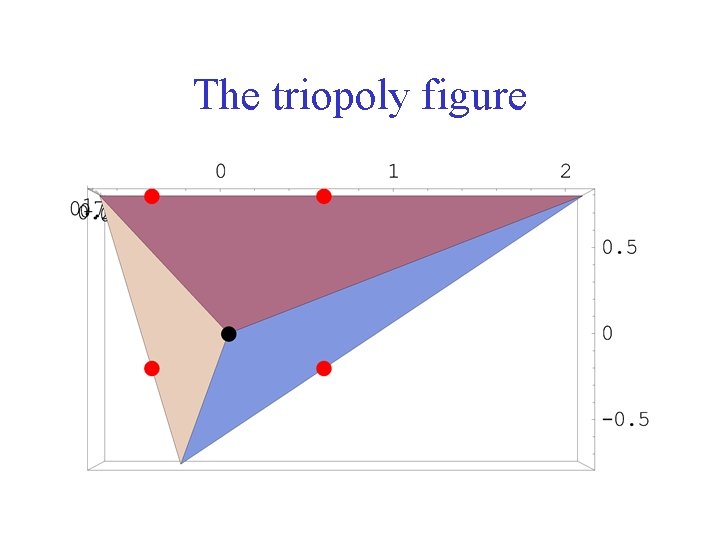
The triopoly figure

This corresponds to

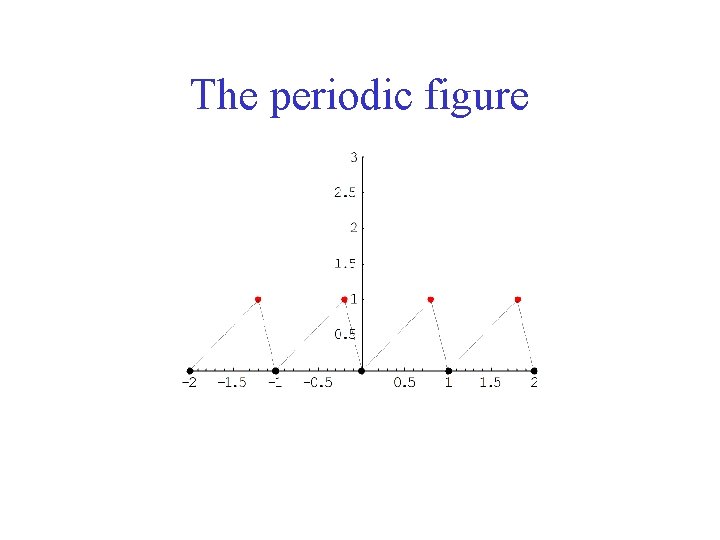
The periodic figure

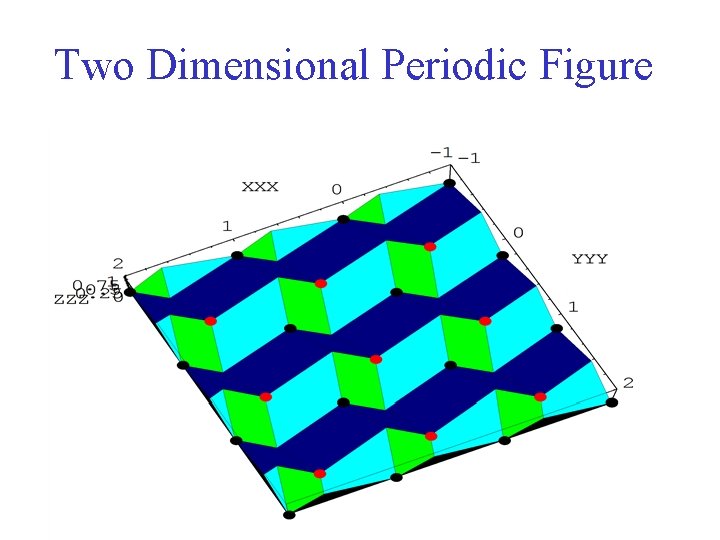
Two Dimensional Periodic Figure

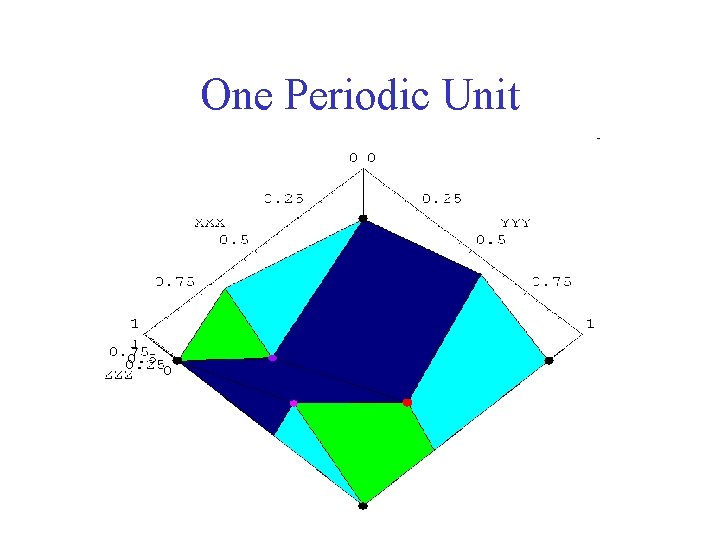
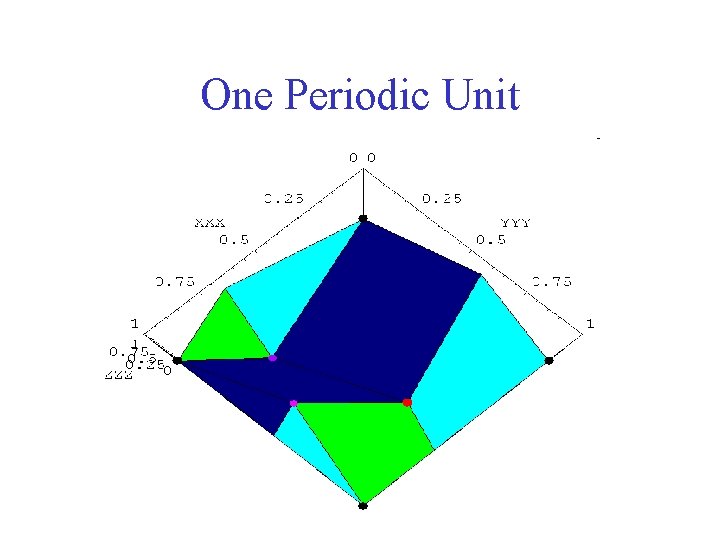
One Periodic Unit

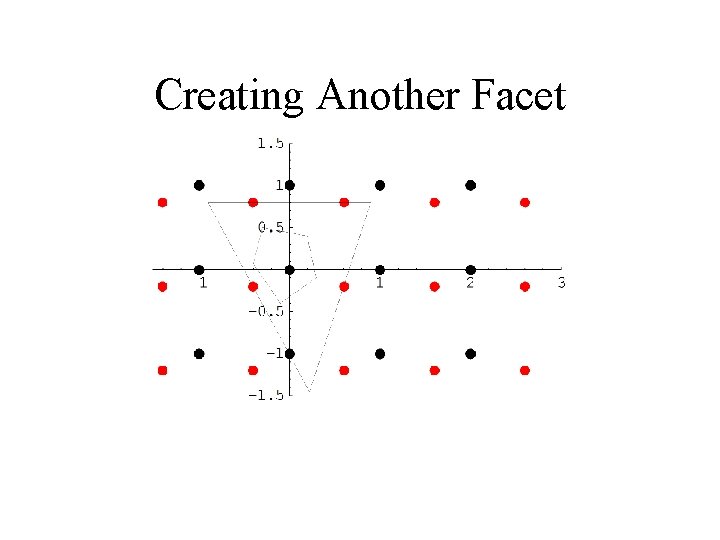
Creating Another Facet

The Periodic Figure - Another Facet

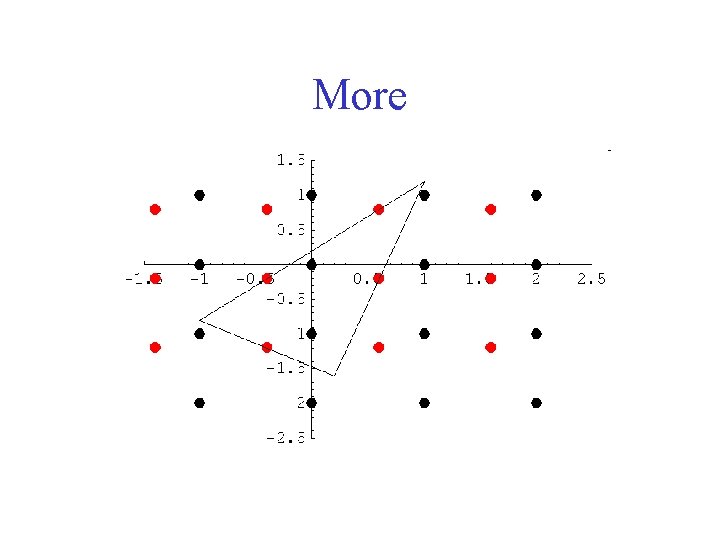
More

But there are four sided figures too Corneujois and Margot have given a complete characterization of the two dimensional cutting planes for the pure continuous problem.

All of the three sided polygons create Facets • • For the continuous problem For the Integer Problem For the General problem Two Dimensional analog of Gomory Mixed Integer Cut

xi Integer ti Continuous

Basis B

Corner Polyhedron Equations

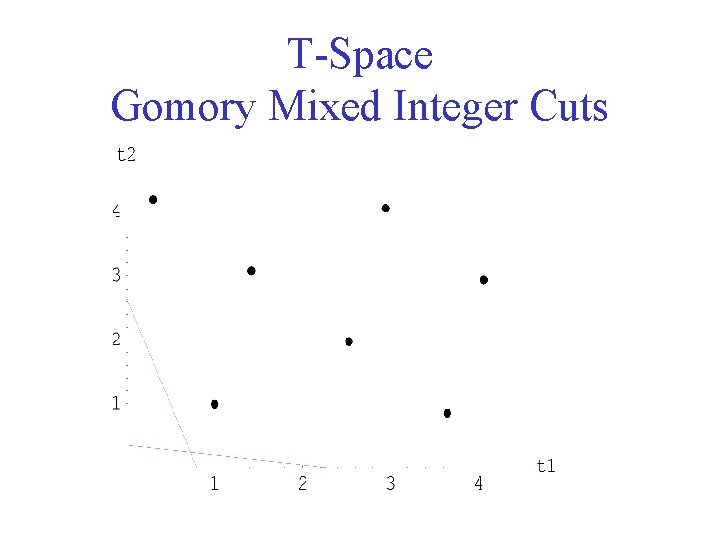
T-Space Gomory Mixed Integer Cuts

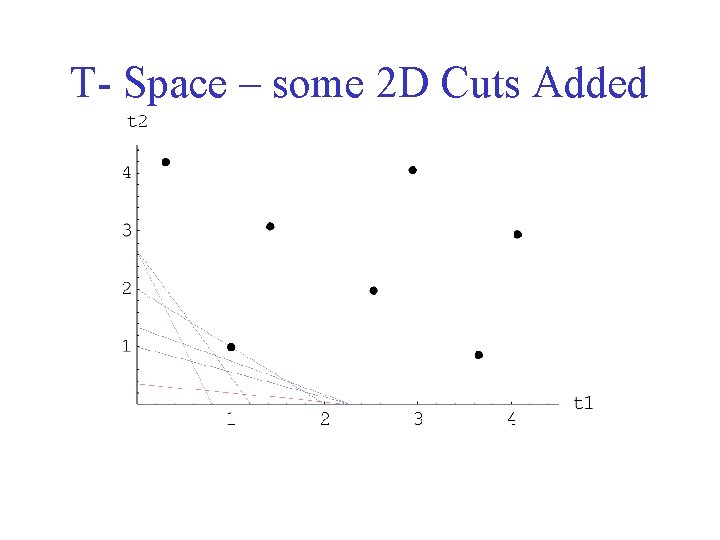
T- Space – some 2 D Cuts Added

Summary • Corner Polyhedra are very structured • The structure can be exploited to create the 2 D facets analogous to the Gomory Mixed Integer Cut • There is much more to learn about Corner Polyhedra and it is learnable

Challenges • Generalize cuts from 2 D to n dimensions • Work with families of cutting planes (like stock cutting) • Introduce data fuzziness to exploit large facets and ignore small ones • Clarify issues about functions that are not piecewise linear.

END

Backup Slides

Thoughts About Integer Programming University of Montreal, January 26, 2007 40 th Birthday Celebration of the Department of Computer Science and Operations Research

Corner Polyhedra and 2 -Dimensional Cuttimg Planes George Nemhauser Symposium June 26 -27 2007

Mod(1) -1 B N has exactly Det(B) distinct Columns vi

One Periodic Unit

Why π(x) Produces the Inequality • It is subadditive π(x) + π(y) π(x+y) on the unit interval (Mod 1) • It has π(x) =1 at the goal point x=f 0

Origin of Continuous Variables Procedure

Shifting

References • “Some Polyhedra Related to Combinatorial Problems, ” Journal of Linear Algebra and Its Applications, Vol. 2, No. 4, October 1969, pp. 451 -558 • “Some Continuous Functions Related to Corner Polyhedra, Part I” with Ellis L. Johnson, Mathematical Programming, Vol. 3, No. 1, North-Holland, August, 1972, pp. 23 -85. • “Some Continuous Functions Related to Corner Polyhedra, Part II” with Ellis L. Johnson, Mathematical Programming, Vol. 3, North-Holland, December 1972, pp. 359 -389. • “T-space and Cutting Planes” Paper, with Ellis L. Johnson, Mathematical Programming, Ser. B 96: Springer-Verlag, pp 341 -375 (2003).