ECE 383 ME 442 More Rigid Transforms 3

ECE 383/ ME 442 More Rigid Transforms, 3 D Rotations

Agenda • Working with transforms • 3 D rotations and representations

Operations on Transforms • Application • Composition • Inversion Accomplish: changes of coordinate frame • Interpolation • Differentiation Accomplish: movement

Composing 2 D transformations •

Rigid Transformation in 3 D • q = (R, tx, ty, tz) with R a 3 x 3 rotation matrix • Robot R 0 R 3 given in reference frame T 0 • What’s the new robot Rq? {Tq(x, y, z) | (x, y, z) R 0} • Define rigid transformation Tq(x, y, z) : R 3 Tq(x, y, z) = R 3 D rotation matrix x y z + tx ty tz Affine translation

3 -D Rigid Rotations r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 (Right-handed coordinate system) n n det(A) = +1 Orthogonal rows and columns: ATA=I, AAT=I ||Ax|| = ||x|| for any x, L 2 norm ||. || Product of two rotations is a rotation (0, 1, 0) (r 11, r 21, r 31) (1, 0, 0) (0, 0, 1) (r 13, r 23, r 33) (1, 0, 0) (0, 0, 1) (r 12, r 22, r 32)

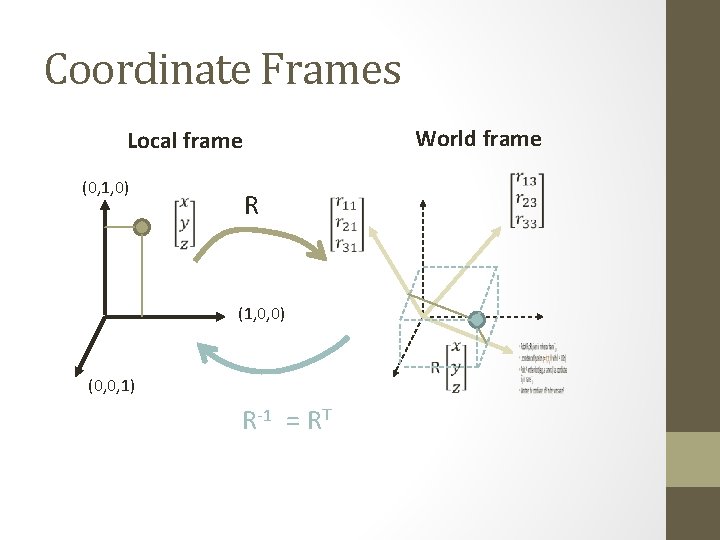
Coordinate Frames World frame Local frame (0, 1, 0) R (1, 0, 0) (0, 0, 1) R-1 = RT

Composing 3 D transformations •

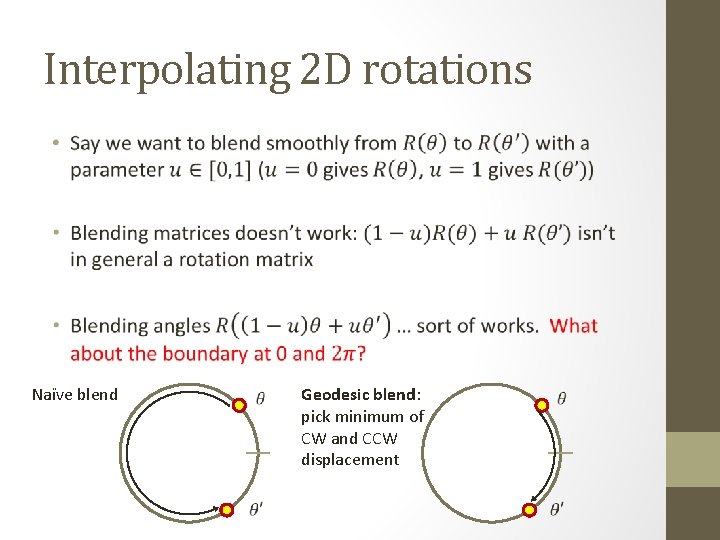
Interpolating 2 D rotations • Naïve blend Geodesic blend: pick minimum of CW and CCW displacement

Topological spaces •

Some Important Topological Spaces • • • R: real number line Rn: N-dimensional Cartesian space S 1: boundary of circle in 2 D S 2: surface of sphere in 3 D SO(2), SO(3): set of 2 D, 3 D orientations (special orthogonal group) SE(2), SE(3): set of rigid 2 D, 3 D transformations (special Euclidean group) • Cartesian product A x B, power notation An = A x A … x A • Homeomorphism ~ denotes topological equivalence • • Continuous mapping with continuous inverse (bijective) Cube ~ S 2 SO(2) ~ S 1 SE(3) ~ SO(3) x R 3

Topology of SO(3) r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 n n n 9 entries, constrained by: Orthogonal rows and columns: ATA=I, AAT=I det(A) = +1 n (+/- 1 is implied by the first condition) 9 variables - 6 non-redundant constraints => SO(3) has 3 degrees of freedom

4 representations of 3 D rotations • • • 3 x 3 rotation matrix R Euler angles REuler(f, q, y) Axis angle RAA(v, q) Quaternion RQuat(q) All representations are “equivalent” but may have certain mathematical or computational advantages

Axis-aligned rotations Rotate about: Z axis cos θ -sin θ 0 sin θ cos θ 0 0 0 1 Y axis cos θ 0 sin θ 0 1 0 -sin θ 0 cos θ X axis 1 0 0 0 cos θ -sin θ 0 sin θ cos θ

Parameterization of SO(3) § Euler angles: (f, q, y) z z y f 1 2 3 4 y q y x x x y

Euler Angles § § Which axes to pick, and what order? Convention A, B, C REuler(f, q, y) = RA(f)RB(q)RC(y) E. g. , ZYZ, ZYX (roll-pitch-yaw), etc

Euler Angles § Which axes to pick, and what order? § Convention A, B, C § REuler(f, q, y) = RA(f)RB(q)RC(y) § E. g. , ZYZ, ZYX (roll-pitch-yaw), etc § Disadvantages § Must constrain to range of values § Singularities, e. g. ZYZ when q=0 or p (Gimbal lock) § Interpolation?

Axis-Angle Representation • Every rotation matrix R can be obtained by rotating the identity matrix by some angle θ about some axis v! • R v = v

Axis-Angle Representation • Axis v (||v||=1), angle θ • Rodrigues’ formula: rotate x about v -> x’ x’ = x cos θ + (v x x) sin θ + v (v. T x) (1 - cos θ) Or in matrix form… RAA(θ, v) = cos θ I + sin θ [v] + (1 - cos θ) v v. T Cross product matrix 0 -vz vy vz 0 -vx -vy vx 0

Recovering Axis and Angle from the Rotation Matrix • θ = Angle(R) = cos-1((r 11+r 22+r 33 -1)/2) = cos-1((tr(R)-1)/2) • v = Axis(R) = 1/(2 sin θ) r 32 -r 23 r 13 -r 31 r 21 -r 12

Properties of Axis-Angle • Disadvantages: • Non unique: RAA(θ, v)=RAA(-θ, -v) (can constrain θ to range [0, p]) • 4 parameters + one unit length constraint ||v||=1; dealing with this constraint is sometimes annoying, for example, in interpolation, optimization, or sampling • Unique encoding: vector w = θv • θ = ||w||, v = w/||w|| • “Exponential map” REM(w) = RAA( ||w|| , w/||w|| )

Quaternion representation • Generalization of complex numbers • Complex z=z 0+i z 1, with |z|=1 can represent a 2 D rotation. What’s the 3 D analogue? q = q 0+q 1 i + q 2 j +q 3 k, where i 2 = j 2 = k 2 = -1 i = jk = -kj j = ki = -ik k = ij = -ji Quaternions were a forerunner of vectors and were once mandatory of all students of physics and math!

Unit quaternion representation • q = (q 0, q 1, q 2, q 3), ||q||=1 RQ(q) = 2(q 02+q 12)-1 2(q 1 q 2+q 0 q 3) 2(q 1 q 3 -q 0 q 2) 2(q 1 q 2 -q 0 q 3) 2(q 02+q 22)-1 2(q 2 q 3+q 0 q 1) • Related to axis angle: • q = (cos q/2, vx sin q/2, vy sin q/2, vz sin q/2) 2(q 1 q 3+q 0 q 2) 2(q 2 q 3 -q 0 q 1) 2(q 02+q 32)-1

Properties of Unit Quaternions • 4 -sphere: 3 D manifold in 4 D space • Non-unique: Double cover of SO(3) • Advantages (widely used in computer animation): • Quaternion multiplication = rotation composition (slightly faster than matrix *) • Curve interpolation formulas (Shoemake, ‘ 85)

Summary • Rotation matrix • • • 9 parameters rij in range [-1, 1] Constraint: determinant +1 Advantages: composition, inversion are easy • Euler angles • • 3 parameters (f, q, y) in range [0, 2 p) Axes picked by convention (e. g. , Roll-Pitch-Yaw) Advantages: no constraints, simple interpolation “works” Disadvantages: multiple representation, singularities, composition & inversion not easy • Axis-angle • • 4 parameters (q, v), q in [0, p] Constraint: |v|=1 Advantages: intuitive, inversion is easy Disadvantages: constraint, composition & interpolation not easy , multiple representation at p • Moment representation (aka exponential map) • • • 3 parameters w (= q*v), ||w||<=p Advantages: no constraints, inversion easy, relation to angular velocity (as we shall see soon) Disadvantages: composition & interpolation not easy, multiple representation at p • Quaternion • • 4 parameters q=(q 0, q 1, q 2, q 3) Constraint: |q|=1 Advantages: composition & interpolation formulas, inversion easy Disadvantages: constraint, multiple representation R(q) = R(-q)

Notion of Distance • θ(R 1 TR 2) = cos-1 ((tr(R 1 TR 2)-1)/2) measures the minimum angle needed to rotate from frame R 1 to R 2 • Makes a good distance metric

Rotation in Motion • • Interpolating between two rotation matrices A and B We want a path X(s) : [0, 1] -> SO(3) with R(0) = A and R(1) = B Let v = Axis(ATB), θ = Angle(ATB) Verify that X(s) = A RAA(sθ, v) satisfies the desired properties Actually a geodesic in SO(3)!

Differentiating 2 D rotations •

Angular Velocities in 2 D •

Angular Velocities in 3 D • For parameterized rotation trajectory REM(wt), we can show: d/dt REM(wt) = [w] REM(wt) • => |w| is the speed of rotation • [w] is the cross product matrix • => w x x is the velocity of some point x, specified in world coordinates, attached to the frame as it rotates • => w is the angular velocity

Recap • 5 operations on transforms: • • • Application to points / directions Composition Inversion Interpolation Differentiation • Four common representations of SO(3) • All four implemented robustly in Python klampt. so 3 module, C++ in Kris. Library/math 3 d • Notion of distance, geodesic, velocity in SO(3)

Next Week • Lab: Intro to Python and Klamp’t