Dynamic Set ADT Dynamic Set Dictionary 1 2

Dynamic Set ADT; Dynamic Set Dictionary 1. 2. 3. 4. 5. 6. 7. Definitions of Dynamic Set and Dictionary Implementation of Dictionary with lists and arrays Implementation with DAT Implementation with hash table using collision resolution by chaining Complexity of the operations under simple uniform hashing Selecting a hash function Applications 1/8/2022 Gerda Kamberova: 10 1

Dynamic Sets ADT n n GOAL: investigate data structures and algorithms that support efficient implementation of various operations on sets. Dynamic sets: may change size over time Key: identifier of an element. Operations: u Search u Insert u Delete u Min u Max u Predecessor u Successor 1/8/2022 Gerda Kamberova: 10 2

Dictionary: Go look it up! n n Primary use: store data so they can be located quickly using keys. Examples of dictionary u the set of bank accounts u the set of windows opened by GUI u student database u the symbol table used by compilers Dictionary ADT: A dynamic set which support Search, Insert, Delete, possibly Update. Hash Table: data structure; implements Dictionary u worst-case time to perform the operations is O(n) u expected time is O(1) Gerda Kamberova Algorithms: Hashing 3

Dictionary ADT x n n n Dictionary of records, T. u Each record has (key, data), u Keys are distinct key u x is a reference to a dictionary record data Operations u insert(T, x): inserts the record pointed to by x into T u delete(T, x), removes record point by x from T u search(T, key), returns a pointer to the record with the given key, or null if no record has that key u update(T, oldrec, newrec), updates the record pointed by oldrec to have the record pointed to by newrec. Example x = search(key) delete(x) Gerda Kamberova Algorithms: Hashing 4

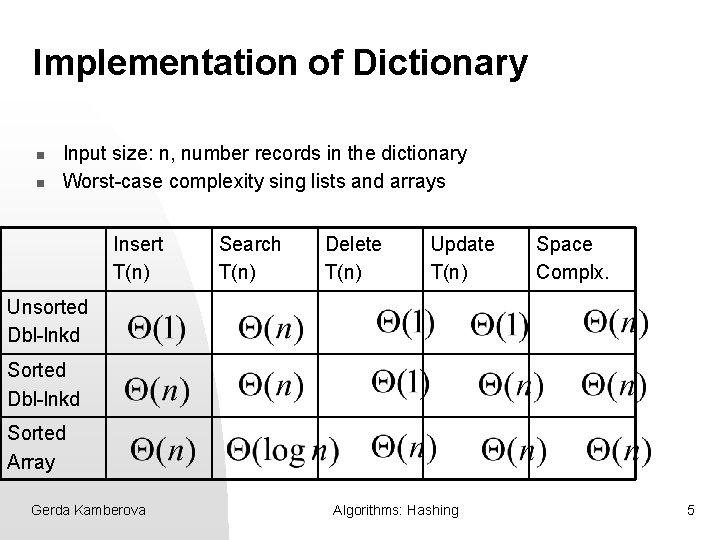
Implementation of Dictionary n n Input size: n, number records in the dictionary Worst-case complexity sing lists and arrays Insert T(n) Search T(n) Delete T(n) Update T(n) Space Complx. Unsorted Dbl-lnkd Sorted Array Gerda Kamberova Algorithms: Hashing 5

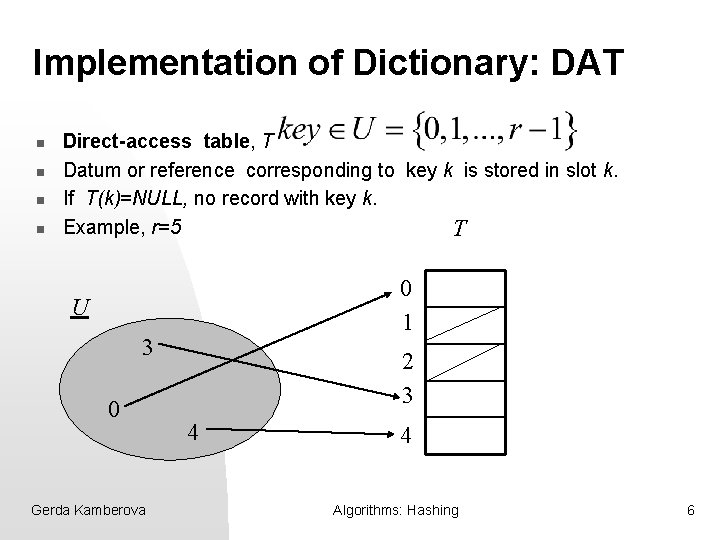
Implementation of Dictionary: DAT n n Direct-access table, T Datum or reference corresponding to key k is stored in slot k. If T(k)=NULL, no record with key k. Example, r=5 T 0 1 U 3 0 Gerda Kamberova 2 3 4 4 Algorithms: Hashing 6

DAT: Complexity of the operations Direct. Address_Search( T, key k) return T[k] Direct. Address_Insert( T, ptr x to element) T[key(x)]=x Direct. Address. Delete( T, ptr x to element) T[key(x)] = NULL n n Each operation time. Moderate r, r<1000 What if the number of keys, n , stored at any particular time much smaller than r? Example: student dictionary, 10^9, n=4000. Gerda Kamberova Algorithms: Hashing 7

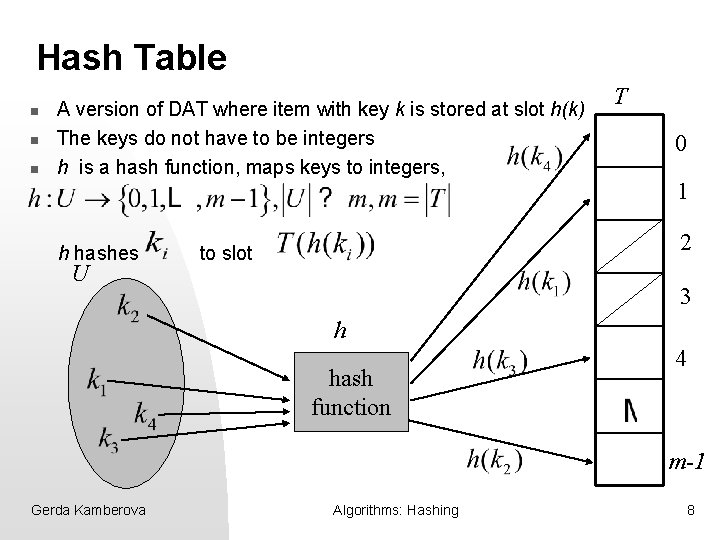
Hash Table n n n A version of DAT where item with key k is stored at slot h(k) The keys do not have to be integers h is a hash function, maps keys to integers, h hashes U T 0 1 2 to slot 3 h hash function 4 m-1 Gerda Kamberova Algorithms: Hashing 8

Hash Tables n n n Hash tables are typically one of the most efficient ways of implementing a Dictionary ADT, particularly if we know something about the distribution of the key values Hash tables do not support efficiently operations that rely on relative order of data elements, for example fining min, max or sorting Since h hashes multiple keys to the same slot. Collision: occurs when two keys hashed to the same slot Cannot avoid collision. Must resolve it. Gerda Kamberova Algorithms: Hashing 9

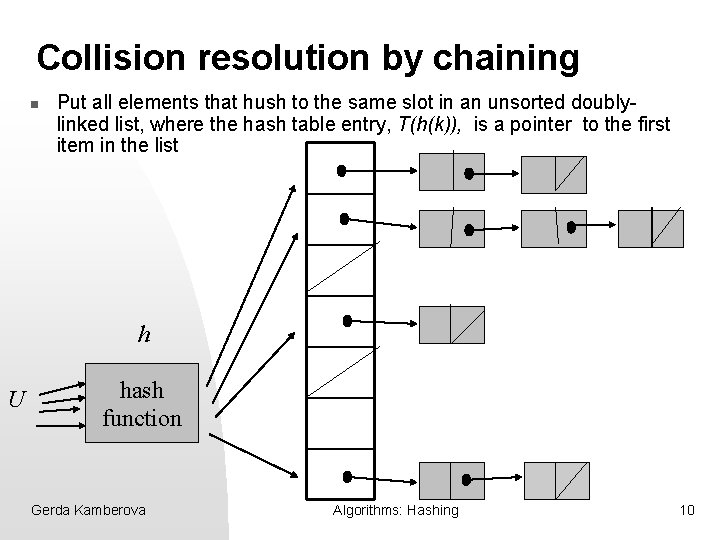
Collision resolution by chaining n Put all elements that hush to the same slot in an unsorted doublylinked list, where the hash table entry, T(h(k)), is a pointer to the first item in the list h U hash function Gerda Kamberova Algorithms: Hashing 10

Implementation of a Dictionary using hashing with collision resolution by chaining n n T is the hash table, x is a ptr to a record key(x) returns the key of the record pointed by x Chained. Hash_Search( T, k ) search key k in the unsorted list T[h(key)] Chained. Hash_Insert( T, x ) insert the record pointed by x at the head of the list T[h(key(x))] Chained. Hash_Delete( T, x ) delete x from the doubly-linked list T[h(key(x))] Gerda Kamberova Algorithms: Hashing 11

Time complexity analysis of hashing with collision resolution by chaining n n n Computing h(k), h(k)= Insert: worst –case Search; worst-case, all keys hash to the same slot, Delete: Update: , (including delete and reinsert if key changes). Load factor , average number keys per slot m = size of the hash table n = number records currently in the dictionary Gerda Kamberova Algorithms: Hashing 12

Average-case time complexity using hashing with collision resolution by chaining n n Assume simple uniform hashing: for any key k, h(k) is equally likely to hash to any of the m slots of the table T Search: the expected time to search is the time to hash the key, plus the expected length of the list at the hashed slot. u Let T(j) the linked list at slot j u Let be R. V. denoting the length of T(j) , j=1, . . , m. u What is the distribution of. For i=0, 1, 2, …, n, Gerda Kamberova Algorithms: Hashing 13

Average-case time complexity using hashing with collision resolution by chaining Search (cont): T(j) is the linked list at slot j, length of T(j) , j=1, . . , m. The distribution of u is RV denoting the : The expected length is Gerda Kamberova Algorithms: Hashing 14

Average-case time complexity using hashing with collision resolution by chaining n Assumed simple uniform hashing n Search: the expected time to search is the expected length to hash, , plus E(T(j)), n u The average-csea complexity for search is i. e. one plus the avg number keys per slot u If , Insert, Delete, Update: Gerda Kamberova Algorithms: Hashing 15

Selecting a hash function (HF) n n A good HF should not give preference to some slots over others HF should distribute keys uniformly, i. e. a key is equally likely to hash to any of the slots – simple uniform hashing (SUH) If the keys are drawn from U according to distribution P, and K the RV representing the key drawn, for SUH: Example: u U=[0, 1] u P is the uniform distribution over [0, 1], h that achieves SUH is given by For m=100, h(0. 5)=50, h(0. 25)=25, … The problem is that we do not know the key distribution P, so we cannot check (1). In practice, heuristics are used to derive HF. u n Gerda Kamberova Algorithms: Hashing 16

Selecting a hash function n Regularity condition: hash function should be independent of any patterns in the data. Similar keys should not hash to similar or close slots Assume keys are natural numbers, if not will re-map them to the naturals. Division Method for selecting HF u u u HF should depend on the complete data (all bits); m should not be power of 2 or 10. Why? m=10000 376218705 593598705 Best select m to be prime, not close to powers of 2 or 10 Given n, « « « decide what load factor (avg search time) the application can tolerate Select m to be prime, close to n/load factor and not close to power of 2 Run experiments and test that h does SUH Gerda Kamberova Algorithms: Hashing 17

Selecting a hash function n Multiplication method u u Define Advantage: value of m is not critical Good choice of A, Usually, m is power of 2 (easy to implement, multiplication by 2 is a shift) Gerda Kamberova Algorithms: Hashing 18

ADT Dictionary n n n Hashing: the preferred way to implement Dictionary Achieves O(1) avg time to search when the load factor is close to 1 (>0. 8 rule of thumb) O(1) time to insert, delete, update Collision resolution: how to deal with keys that hash to the same slot. Collision resolution by chaining maintains unsorted doubly linked lists at the slots (overhead for maintaining the lists) Selecting a hush function: u Division method u Multiplication method Gerda Kamberova Algorithms: Hashing 19

Applications of hashing n n Compiler use hashing in symbol table implementation (to keep track of defined variables). Graph problems where nodes are identified by names instead numbers Game playing software: to keep transposition table (of already encountered lines of play) On-line spell checkers (without error correction). The whole dictionary is pre-hashed and words can be checked in constant time. Gerda Kamberova Algorithms: Hashing 20