The Dictionary ADT Definition A dictionary is an














- Slides: 21

The Dictionary ADT Definition A dictionary is an ordered or unordered list of key-element pairs, where keys are used to locate elements in the list. Example: consider a data structure that stores bank accounts; it can be viewed as a dictionary, where account numbers serve as keys for identification of account objects. Operations (methods) on dictionaries: size () Returns the size of the dictionary empty () Returns true is the dictionary is empty find. Item (key) Locates the item with the specified key. If no such key exists, sentinel value NO_SUCH_KEY is returned. If more than one item with the specified key exists, an arbitrary item is returned. find. All. Items (key) Locates all items with the specified key. If no such key exists, sentinel value NO_SUCH_KEY is returned. remove. Item (key) Removes the item with the specified key remove. All. Items (key) Removes all items with the specified key insert. Item (key, element) Inserts a new key-element pair

Additional methods for ordered dictionaries closest. Key. Before (key) closest. Elem. Before (key) closest. Key. After (key) closest. Elem. After (key) Returns the key of the item with largest key less than or equal to key Returns the element for the item with largest key less than or equal to key Returns the key of the item with smallest key greater than or equal to key Returns the element for the item with smallest key greater than or equal to key Sentinel value NO_SUCH_KEY is always returned if no item in the dictionary satisfies the query. Note Java has a built-in abstract class java. util. Dictionary In this class, however, having two items with the same key is not allowed. If an application assumes more than one item with the same key, an extended version of the Dictionary class is required.

Example of unordered dictionary Consider an empty unordered dictionary and the following set of operations: Operation Dictionary Output insert. Item(5, A) {(5, A)} insert. Item(7, B) {(5, A), (7, B)} insert. Item(2, C) {(5, A), (7, B), (2, C)} insert. Item(8, D) {(5, A), (7, B), (2, C), (8, D)} insert. Item(2, E) {(5, A), (7, B), (2, C), (8, D), (2, E)} find. Item(7) {(5, A), (7, B), (2, C), (8, D), (2, E)} B find. Item(4) {(5, A), (7, B), (2, C), (8, D), (2, E)} NO_SUCH_KEY find. Item(2) {(5, A), (7, B), (2, C), (8, D), (2, E)} C find. All. Items(2) {(5, A), (7, B), (2, C), (8, D), (2, E)} C, E size() {(5, A), (7, B), (2, C), (8, D), (2, E)} 5 remove. Item(5) {(7, B), (2, C), (8, D), (2, E)} A remove. All. Items(2) {(7, B), (8, D)} C, E find. Item(4) {(7, B), (8, D)} NO_SUCH_KEY

Example of ordered dictionary Consider an empty ordered dictionary and the following set of operations: Operation Dictionary Output insert. Item(5, A) {(5, A)} insert. Item(7, B) {(5, A), (7, B)} insert. Item(2, C) {(2, C), (5, A), (7, B)} insert. Item(8, D) {(2, C), (5, A), (7, B), (8, D)} insert. Item(2, E) {(2, C), (2, E), (5, A), (7, B), (8, D)} find. Item(7) {(2, C), (2, E), (5, A), (7, B), (8, D)} B find. Item(4) {(2, C), (2, E), (5, A), (7, B), (8, D)} NO_SUCH_KEY find. Item(2) {(2, C), (2, E), (5, A), (7, B), (8, D)} C find. All. Items(2) {(2, C), (2, E), (5, A), (7, B), (8, D)} C, E size() {(2, C), (2, E), (5, A), (7, B), (8, D)} 5 remove. Item(5) {(2, C), (2, E), (7, B), (8, D)} A remove. All. Items(2) {(7, B), (8, D)} C, E find. Item(4) {(7, B), (8, D)} NO_SUCH_KEY

Implementations of the Dictionary ADT Dictionaries are ordered or unordered lists. The easiest way to implement a list is by means of an ordered or unordered sequence. Unordered sequence implementation Items are added to the initially empty dictionary as they arrive. insert. Item(key, element) method is O(1) no matter whether the new item is added at the beginning or at the end of the dictionary. find. Item(key), find. All. Items(key), remove. Item(key) and remove. All. Items(key) methods, however, have O(n) efficiency. Therefore, this implementation is appropriate in applications where the number of insertions is very large in comparison to the number of searches and removals. Ordered sequence implementation Items are added to the initially empty dictionary in nondecreasing order of their keys. insert. Item(key, element) method is O(n), because a search for the proper place of the item is required. If the sequence is implemented as an ordered array, remove. Item(key) and remove. All. Items(key) take O(n) time, because all items following the item removed must be shifted to fill in the gap. If the sequence is implemented as a doubly linked list , all methods involving search also take O(n) time. Therefore, this implementation is inferior compared to unordered sequence implementation. However, the efficiency of the search operation can be considerably improved, in which case an ordered sequence implementation will become a better choice.

Implementations of the Dictionary ADT (contd. ) Array-based ranked sequence implementation A search for an item in a sequence by its rank takes O(1) time. We can improve search efficiency in an ordered dictionary by using binary search; thus improving the run time efficiency of insert. Item(key, element), remove. Item(key) and remove. All. Items(key) to O(log n). More efficient implementations of an ordered dictionary are binary search trees and AVL trees which are binary search trees of a special type. The best way to implement an unordered dictionary is by means of a hash table. We discuss AVL trees and hash tables next.

AVL trees Definition An AVL tree is a binary tree with an ordering property where the heights of the children of every internal node differ by at most 1. Example 44 (4) 17 (2) 78 (3) 32 (1) 50 (2) 48 (1) 88 (1) 62 (1) Note: 1. Every subtree of an AVL tree is also an AVL tree. 2. The height of an AVL tree storing n keys is O(log n).

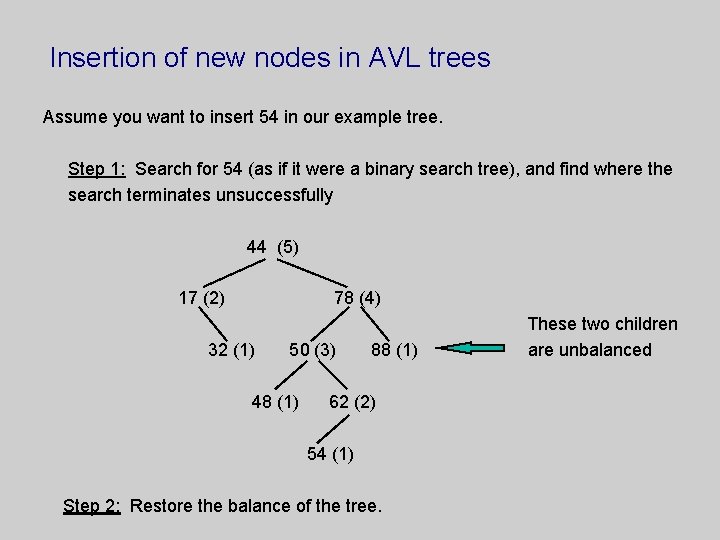
Insertion of new nodes in AVL trees Assume you want to insert 54 in our example tree. Step 1: Search for 54 (as if it were a binary search tree), and find where the search terminates unsuccessfully 44 (5) 17 (2) 78 (4) 32 (1) 50 (3) 48 (1) 88 (1) 62 (2) 54 (1) Step 2: Restore the balance of the tree. These two children are unbalanced

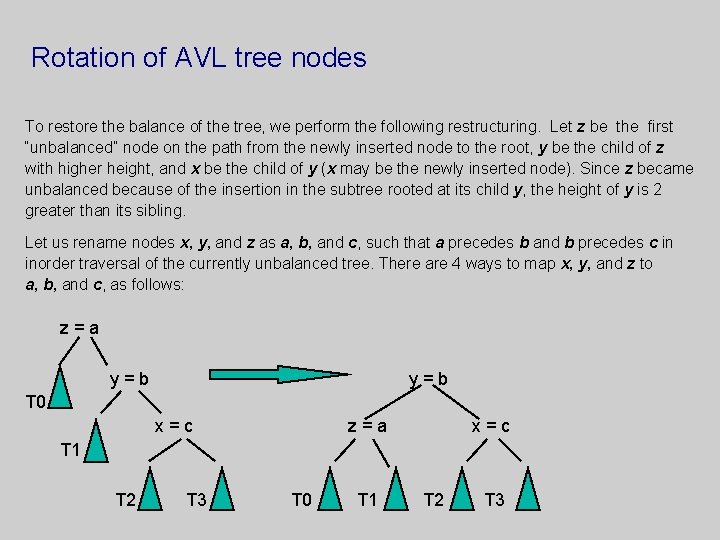
Rotation of AVL tree nodes To restore the balance of the tree, we perform the following restructuring. Let z be the first “unbalanced” node on the path from the newly inserted node to the root, y be the child of z with higher height, and x be the child of y (x may be the newly inserted node). Since z became unbalanced because of the insertion in the subtree rooted at its child y, the height of y is 2 greater than its sibling. Let us rename nodes x, y, and z as a, b, and c, such that a precedes b and b precedes c in inorder traversal of the currently unbalanced tree. There are 4 ways to map x, y, and z to a, b, and c, as follows: z=a y=b T 0 x=c z=a x=c T 1 T 2 T 3 T 0 T 1 T 2 T 3

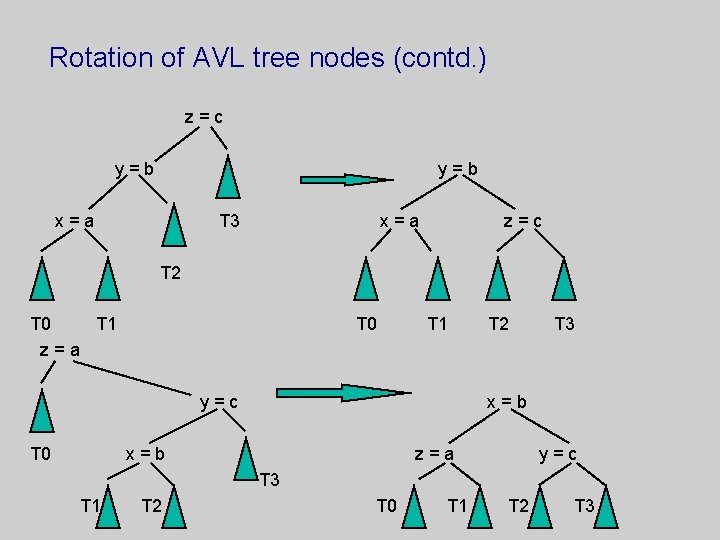
Rotation of AVL tree nodes (contd. ) z=c y=b x=a T 3 x=a z=c T 2 T 0 T 1 z=a T 0 T 1 y=c T 0 T 2 T 3 x=b z=a y=c T 3 T 1 T 2 T 0 T 1 T 2 T 3

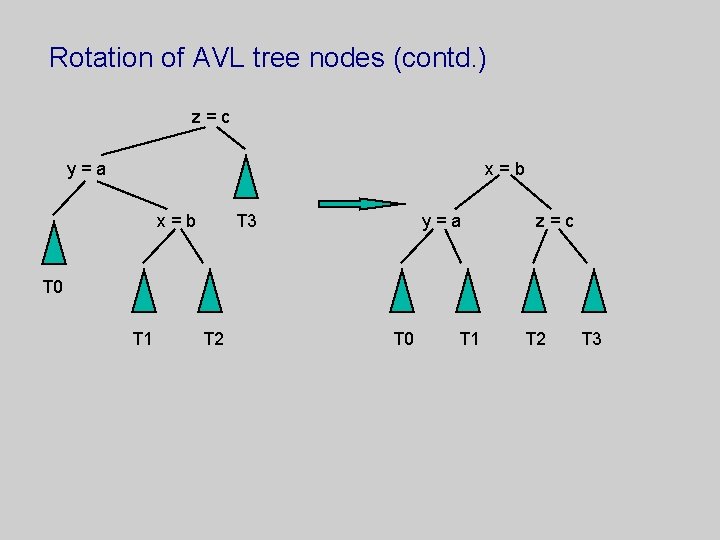
Rotation of AVL tree nodes (contd. ) z=c y=a x=b T 3 y=a z=c T 0 T 1 T 2 T 3

The restructure algorithm Algorithm restructure(x): Input: A node x that has a parent node y, and a grandparent node z. Output: Tree involving nodes x, y and z restructured. 1. Let (a, b, c) be inorder listing of nodes x, y and z, and let (T 0, T 1, T 2, T 3) be inorder listing of the four children subtrees of x, y, and z. 2. Replace the subtree rooted at z with a new subtree rooted at b. 3. Let a be the left child of b and let T 0 and T 1 be the left and right subtrees of a, respectively. 4. Let c be the right child of b and let T 2 and T 3 be the left and right subtrees of c, respectively. If y = b, we have a single rotation, where y is rotated over z. If x = b, we have a double rotation, where x is first rotated over y, and then over z.

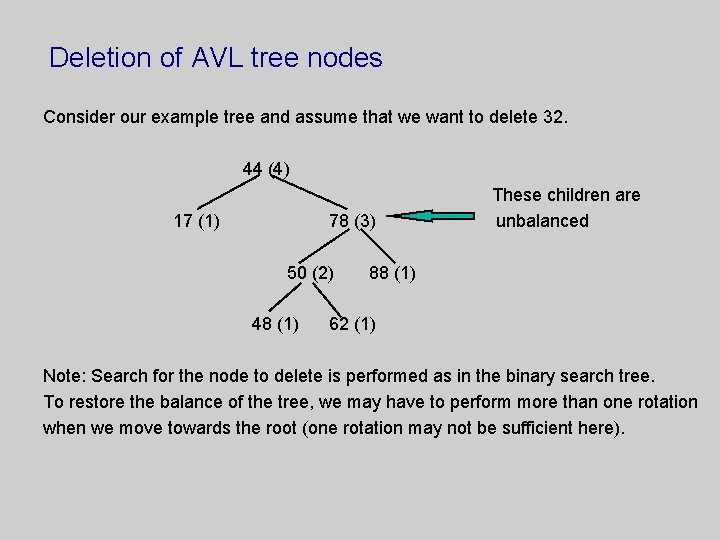
Deletion of AVL tree nodes Consider our example tree and assume that we want to delete 32. 44 (4) 17 (1) 78 (3) 50 (2) 48 (1) These children are unbalanced 88 (1) 62 (1) Note: Search for the node to delete is performed as in the binary search tree. To restore the balance of the tree, we may have to perform more than one rotation when we move towards the root (one rotation may not be sufficient here).

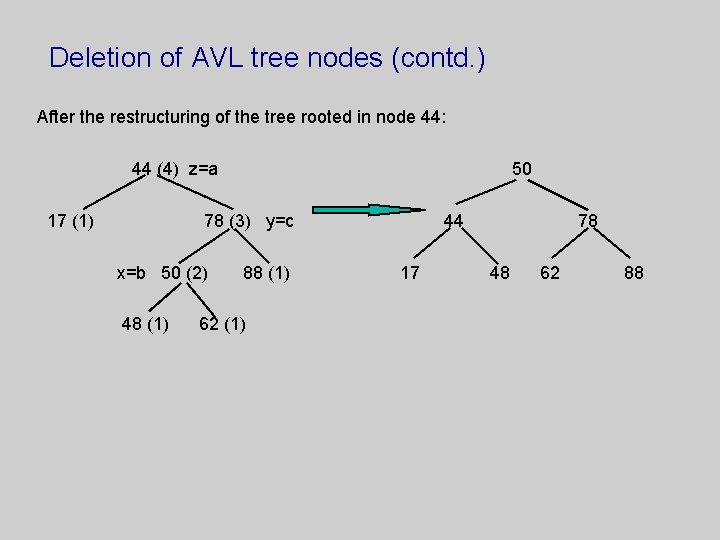
Deletion of AVL tree nodes (contd. ) After the restructuring of the tree rooted in node 44: 44 (4) z=a 17 (1) 50 78 (3) y=c x=b 50 (2) 48 (1) 88 (1) 62 (1) 44 17 78 48 62 88

Implementation of unordered dictionaries: hash tables Hashing is a method for directly referencing an element in a table by performing arithmetic transformations on keys into table addresses. This is carried out in two steps: Step 1: Computing the so-called hash function H: K -> A. K 1 K 2 K 3. . . Kn A 1 A 2. . . An Step 2: Collision resolution, which handles cases where two or more different keys hash to the same table address.

Implementation of hash tables Hash tables consist of two components: a bucket array and a hash function. Consider a dictionary, where keys are integers in the range [0, N-1]. Then, an array of size N can be used to represent the dictionary. Each entry in this array is thought of as a “bucket” (which is why we call it a “bucket array”). An element e with key k is inserted in A[k]. Bucket entries associated with keys not present in the dictionary contain a special NO_SUCH_KEY object. If the dictionary contains elements with the same key, then two or more different elements may be mapped to the same bucket of A. In this case, we say that a collision between these elements has occurred. One easy way to deal with collisions is to allow a sequence of elements with the same key, k, to be stored in A[k]. Assuming that an arbitrary element with key k satisfies queries find. Item(k) and remove. Item(k), these operations are now performed in O(1) time, while insert. Item(k, e) needs only to find where on the existing list A[k] to insert the new item, e. The drawback of this is that the size of the bucket array is the size of the set from which key are drawn, which may be huge.

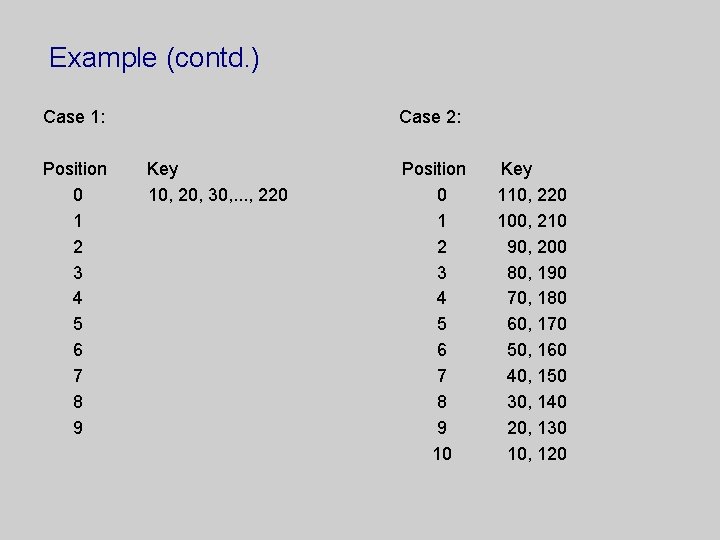
Hash functions We can limit the size of the bucket array to almost any size; however, we must provide a way to map key values into array index values. This is done by an appropriately selected hash function, h(k). The simplest hash function is h(k) = k mod N where k can be very large, while N can be as small as we want it to be. That is, the hush function converts a large number (the key) into a smaller number serving as an index in the bucket array. Example. Consider the following list of keys: 10, 20, 30, 40, . . . , 220. Let us consider two different sizes of the bucket array: (1) a bucket array of size 10, and (2) a bucket array of size 11.

Example (contd. ) Case 1: Position 0 1 2 3 4 5 6 7 8 9 Case 2: Key 10, 20, 30, . . . , 220 Position 0 1 2 3 4 5 6 7 8 9 10 Key 110, 220 100, 210 90, 200 80, 190 70, 180 60, 170 50, 160 40, 150 30, 140 20, 130 10, 120

Example 2 Consider a dictionary of strings of characters from a to z. Assume that each character is encoded by means of 5 bits, i. e. character a b c d e. . . k. . . y code 000010 00011 00100 001011 11001 Then, the string akey has the following code (00001 01011 00101 11001)2 = (44217)10 Assume that our hash table has 101 buckets. Then, h(44217) = 44217 mod 101 = 80 That is, the key of the string akey hashes to position 80. If you do the same with the string barh, you will see that it hashes to the same position, 80.

Hash functions (contd. ) These examples suggest that if N is a prime number, the hash function helps spread out the distribution of hashed values. If dictionary elements are spread fairly evenly in the hash table, the expected running times of operations find. Item, insert. Item and remove. Item are O(n/N), where n is the number of elements in the dictionary, and N is the size of the bucket array. These efficiencies are ever better, O(1), if no collision occurs (in which case only a call to the hash function and a single array reference are needed to insert or find an item).

Collision resolution There are 2 main ways to perform collision resolution: 1 Open addressing. 2 Chaining. In our examples, we have assumed that collision resolution is performed by chaining, i. e. traversing the linked list holding items with the same key in order to find the one we are searching for, or insert a new item with that key. In open addressing we deal with collision by finding another, unoccupied location elsewhere in the array. The easiest way to find such a location is called linear probing. The idea is the following. If a collision occurs when we are inserting a new item into a table, we simply probe forward in the array, one step at a time, until we find an empty slot where to store the new item. When we remove an item, we start by calculating the hash function and test the identified index location. If the item is not there, we examine each array entry from the index location until: (1) the item is found; (2) an empty location is encountered, or (3) the array end is reached.