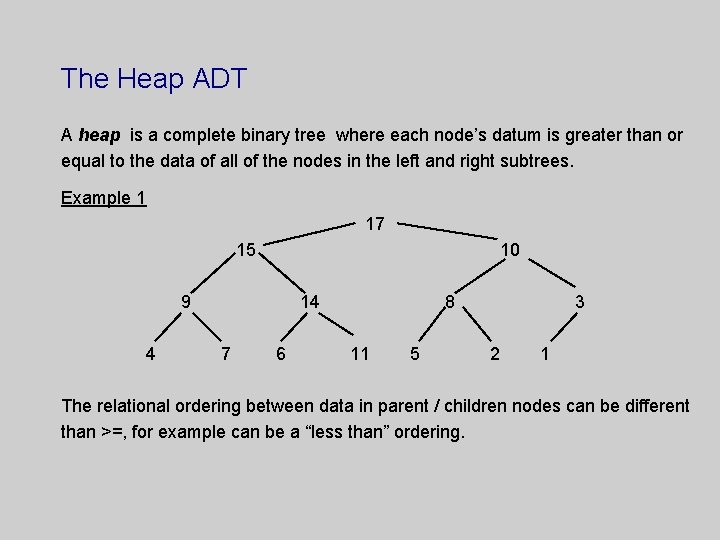
The Heap ADT A heap is a complete

The Heap ADT A heap is a complete binary tree where each node’s datum is greater than or equal to the data of all of the nodes in the left and right subtrees. Example 1 17 15 10 9 4 14 7 6 8 11 5 3 2 1 The relational ordering between data in parent / children nodes can be different than >=, for example can be a “less than” ordering.

Operations on heaps All heap operations are based on the following idea: 1 2. Make a simple structural modification of the heap (different for different operations), which may result in a violation of the heap condition. Traverse the heap from the root to the bottom, or from the bottom to the root (depending on the operation) to recover the heap condition everywhere. The most important operations on heaps are: – – insert. Item (item) remove. Item () Inserts item Removes the root and returns the datum stored

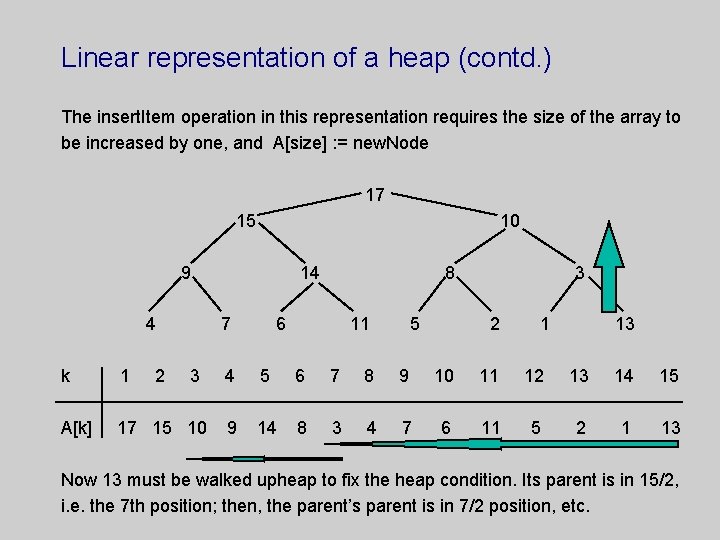
Linear representation of a heap The easiest way to represent a complete binary tree is by means of a onedimensional array of size 2 h+1 - 1, where h is the height of the tree. The most attractive property of this representation is that given a position of a node, j, positions of its parent and children can be easily defined (j / 2 is the position of the parent, j * 2 is the position of the left child, and j *2 + 1 is the position of the right child. Our example 1 heap can be represented as follows: k 1 2 3 A[k] 17 15 10 4 5 6 7 8 9 10 11 12 13 14 9 14 8 3 4 7 6 11 5 2 1

Linear representation of a heap (contd. ) The insert. Item operation in this representation requires the size of the array to be increased by one, and A[size] : = new. Node 17 15 10 9 4 2 14 7 k 1 3 A[k] 17 15 10 8 6 11 5 3 2 1 13 4 5 6 7 8 9 10 11 12 13 14 15 9 14 8 3 4 7 6 11 5 2 1 13 Now 13 must be walked upheap to fix the heap condition. Its parent is in 15/2, i. e. the 7 th position; then, the parent’s parent is in 7/2 position, etc.

The upheap method Algorithm upheap (A[n], j, precedes) Input: array A[n] representing the heap, index of the child’s node j, precedes, a comparator object defining the ordering relationship Output: array A[n] with data originally in j walked up until accordingly ordered with its parent (according to the precedes function) int l : = j int key : = A[l] int k : = l/2 while (k >= 1) and precedes(A[k], key) { A[l] : = A[k] l : = k k : = l/2 } A[l] : = key

The insert. Item method Algorithm insert. Item (H, Item, precedes) Input: heap H[size], item to be inserted precedes, a comparator object defining the ordering relationship Output: boolean variable success set to true if insert. Item is successful if H. full() success : = false else { success : = true size : = size + 1 H[size] : = Item upheap(H[size], size, precedes) } return success The efficiency if insert. Item operation is O(log n), where n is the number of tree nodes.

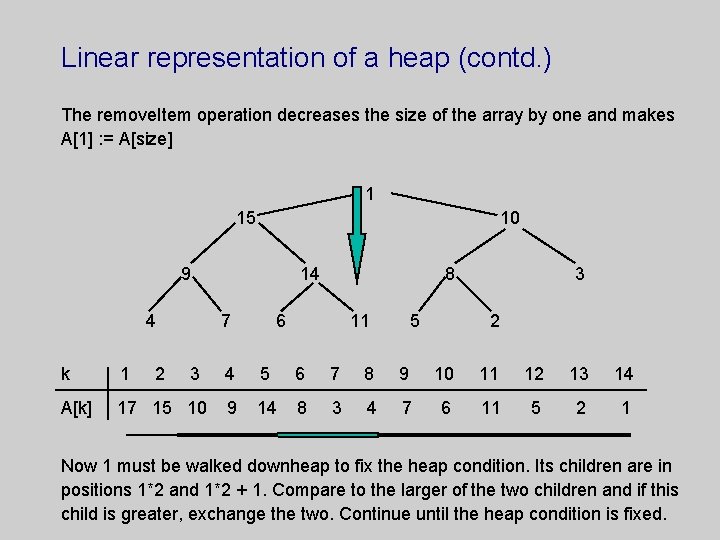
Linear representation of a heap (contd. ) The remove. Item operation decreases the size of the array by one and makes A[1] : = A[size] 1 15 10 9 4 2 14 7 k 1 3 A[k] 17 15 10 8 6 11 5 3 2 4 5 6 7 8 9 10 11 12 13 14 9 14 8 3 4 7 6 11 5 2 1 Now 1 must be walked downheap to fix the heap condition. Its children are in positions 1*2 and 1*2 + 1. Compare to the larger of the two children and if this child is greater, exchange the two. Continue until the heap condition is fixed.

The downheap method Algorithm downheap (A[n], j, precedes) Input: array A[n] representing the heap, index of the parent’s node j, precedes, a comparator object defining the ordering relationship Output: array A[n] with data originally in j walked down until accordingly ordered w. r. t both of its children (according to the precedes function) boolean found. Spot : = false int l : = j int key : = A[l] int k : = 2 * l // get the left child first while (k <= n) and (! found. Spot) { if (k < n) and (! precedes (A[k+1], A[k]]) k : = k + 1 if (! precedes (A[k], key)) A[l] : = A[k], l : = k, k : = 2 * l else found. Spot : = true } // end while A[l] : = key

The remove. Item method Algorithm remove. Item (H, precedes) Input: heap H[size], precedes, a comparator object defining the ordering relationship Output: boolean variable success set to true if remove. Item is successful if H. empty() success : = false else { success : = true item : = H[1] : = H[size] size : = size - 1 downheap(H[size], 1, precedes)} return success The efficiency of remove. Item operation is O(log n), where n is the number of tree nodes.

Heap Sort The idea: build a heap containing the elements to be sorted, then remove them in order. Let n be the size of the heap, and m be the number of elements to be sorted. The following two steps implement heap sort: Step 1: Construct the heap by doing m insert. Item operations. Step 2: Do m remove. Item operations, putting the elements removed from the heap into the place just vacated by the shrinking heap. Advantages of heap sort: 1 All heap methods, including remove. Item and insert. Item are O(log n) methods, i. e. each of the two steps takes O(n log n) time. Ignoring the constant of proportionality, runtime efficiency of heap sort is O(n log n) - much better compared to the quadratic runtime for elementary sorting methods. 2 Heap sort is in-place sorting method, i. e. uses no extra memory

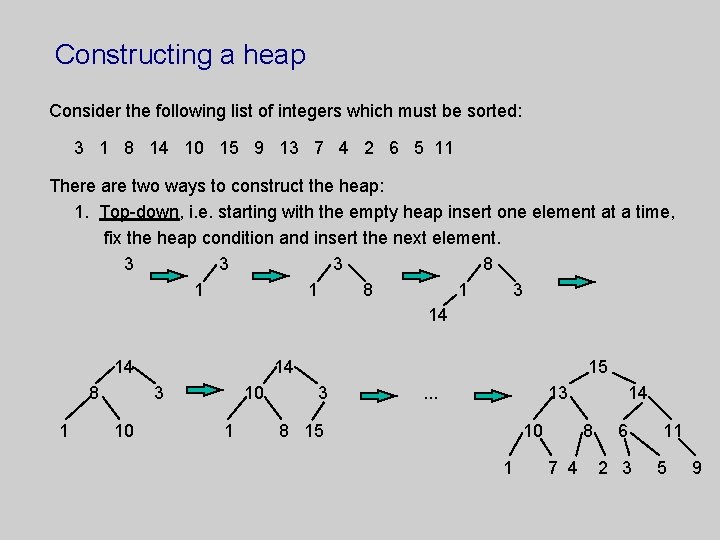
Constructing a heap Consider the following list of integers which must be sorted: 3 1 8 14 10 15 9 13 7 4 2 6 5 11 There are two ways to construct the heap: 1. Top-down, i. e. starting with the empty heap insert one element at a time, fix the heap condition and insert the next element. 3 3 3 8 1 1 8 1 3 14 14 8 1 14 3 10 10 1 15 3 . . . 13 8 15 10 1 14 8 7 4 6 2 3 11 5 9

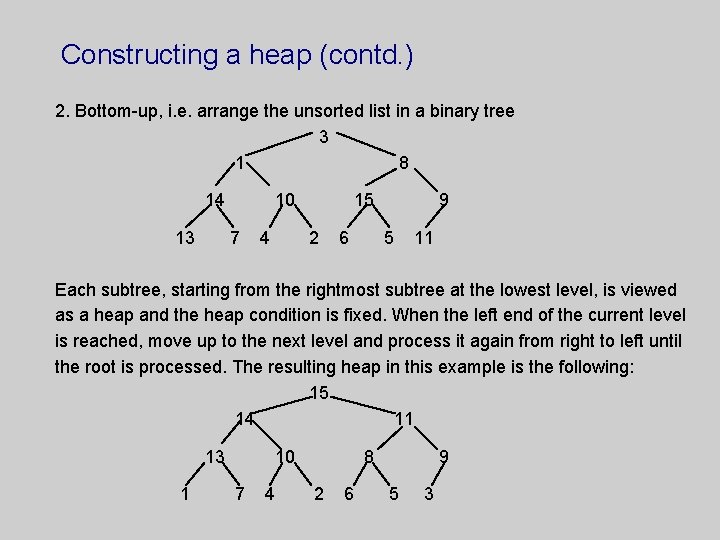
Constructing a heap (contd. ) 2. Bottom-up, i. e. arrange the unsorted list in a binary tree 3 1 8 14 13 10 7 4 15 2 6 9 5 11 Each subtree, starting from the rightmost subtree at the lowest level, is viewed as a heap and the heap condition is fixed. When the left end of the current level is reached, move up to the next level and process it again from right to left until the root is processed. The resulting heap in this example is the following: 15 14 11 13 1 10 7 4 8 2 6 9 5 3

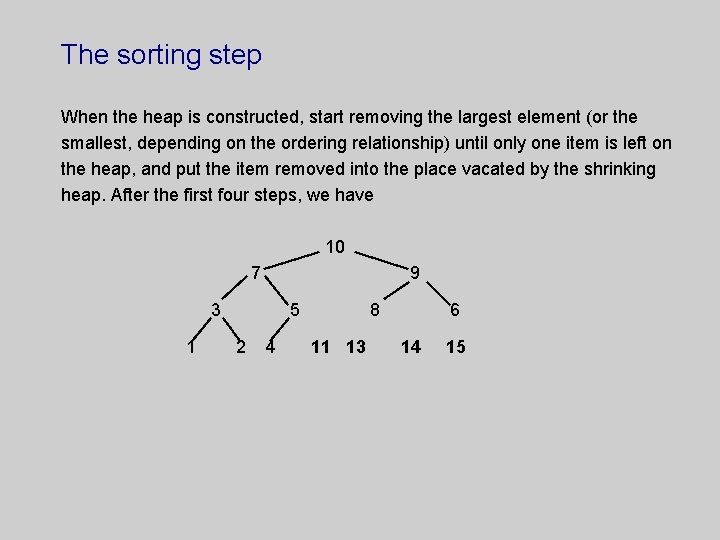
The sorting step When the heap is constructed, start removing the largest element (or the smallest, depending on the ordering relationship) until only one item is left on the heap, and put the item removed into the place vacated by the shrinking heap. After the first four steps, we have 10 7 9 3 1 5 2 4 8 11 13 6 14 15

The heap. Sort method (assuming bottom-up construction) Algorithm heap. Sort (A[n], precedes) Input: array A[n] representing the heap, precedes, a comparator object defining the ordering relationship Output: array A[n] represented a sorted (according to the precedes function) list. int y : = n / 2 while (y > 0) { downheap (A[n], y, precedes) y : = y - 1 } y : = n while (y > 1) { temp : = A[1], A[1] : = A[y], A[y] : = temp, y : = y - 1 downheap(A[y], 1, precedes) } O(n/2 log n) O(n log n) Overall efficiency: O(1. 5 n log n)