Discounted Deterministic Markov Decision Processes and Discounted AllPairs

Discounted Deterministic Markov Decision Processes and Discounted All-Pairs Shortest Paths Omid Madani – SRI International, AI center Mikkel Thorup – AT&T Labs, Research Uri Zwick – Tel Aviv University

Markov Decision Processes [Bellman ’ 57] [Howard ’ 60] … States Actions Costs/Rewards Distributions … Strategies Objectives

Markov Decision Processes [Bellman ’ 57] [Howard ’ 60] … i-th action taken Limiting average version Discounted version Discount factor Optimal positional strategies can be found using LP Is there a strongly polynomial time algorithm?

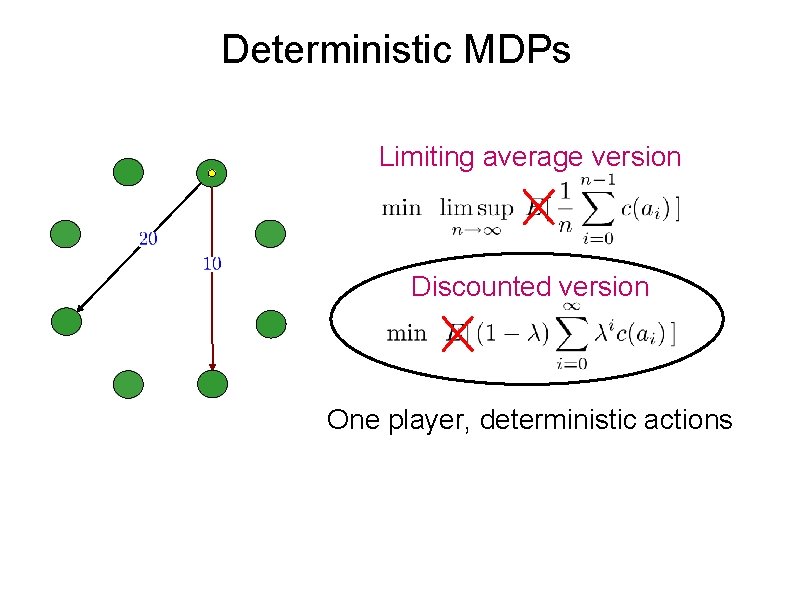
Deterministic MDPs Limiting average version Discounted version One player, deterministic actions

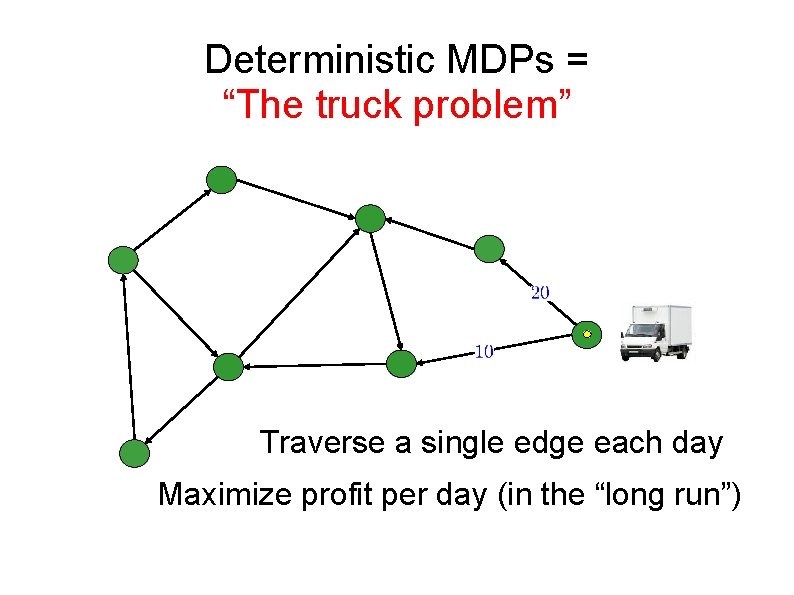
Deterministic MDPs = “The truck problem” Traverse a single edge each day Maximize profit per day (in the “long run”)

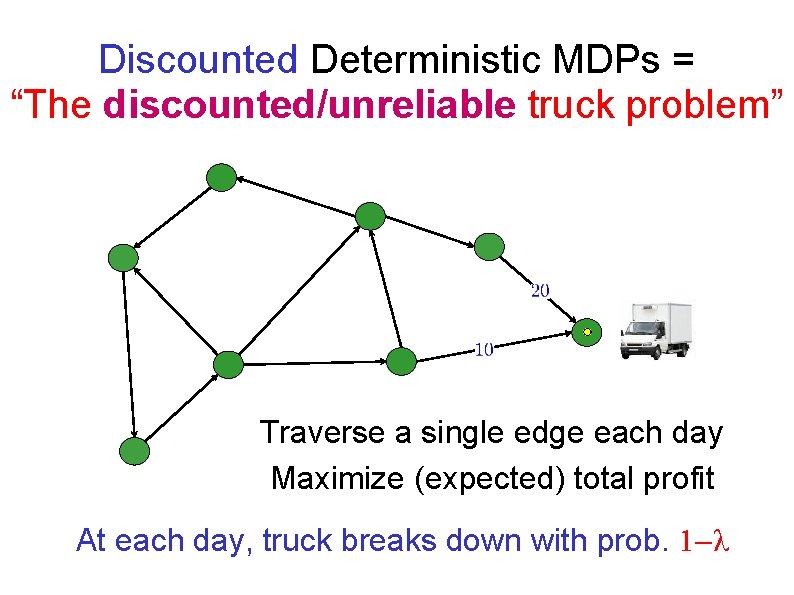
Discounted Deterministic MDPs = “The discounted/unreliable truck problem” Traverse a single edge each day Maximize (expected) total profit At each day, truck breaks down with prob. 1 λ

Deterministic MDPs – limiting average version For each vertex, find a cycle of minimum mean cost reachable from it [Karp ’ 78] [Young-Tarjan-Orlin ’ 91] O(mn) O(mn+n 2 log n) Better performance in practice

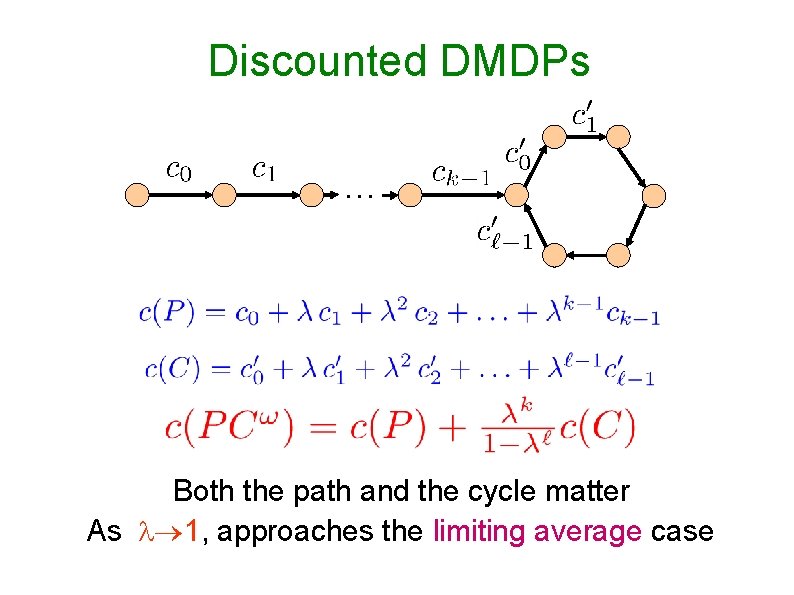
Discounted DMDPs … Both the path and the cycle matter As 1, approaches the limiting average case

Discounted DMDPs – optimal strategies

Discounted DMDPs - results Authors Running time Papadimitriou-Tsitsiklis ’ 87 Madani ’ 02 Andersson-Vorobyov ’ 06 O(n 4) O(mn 2 log n) O(mn 2) New O(mn) O(mn+n 2 log n) n – number of states/vertices m – number of actions/edges

Karp’s algorithm for finding minimum mean cost cycles [Karp’ 78] dk(u) - the smallest cost of a k-edge path starting at u Complexity: O(mn) A cheapest n-edge path starting at v There is a vertex v such that all cycles on Pn(v) are optimal [Madani ’ 00]

Discounted DMDPs x(u) - The smallest discounted cost of an infinite path starting at u Each vertex has an optimal outgoing edge

A Karp-like/Value-iteration algorithm for DMDPs dk(u) - smallest discounted cost of a k-path starting at u Claim 1: For every v V we have x(v) y(v) Claim 2: On every optimal cycle there is at least one vertex v such that x(v) = y(v) How do we know who are the optimal cycles?

Discounted DMDPs – optimal strategies

A Karp-like algorithm for DMDPs First Bellman-Ford phase: k = 1, 2, …, n A Karp phase: Second Bellman-Ford phase: k = 1, 2, …, n Theorem: For every v V we have x(v)=yn(v)

The Andersson-Vorobyov algorithm [’ 06] We want to solve the following equations: Start with values that satisfy: If each vertex has a tight out-going edge, we are done Otherwise, increase values, in a controlled manner

The Andersson-Vorobyov algorithm [’ 06] For each vertex, select an outgoing tight edge, if any. The result is a pseudo-forest. Cannot Ideal! become tight val(u) c(u, v) + val(v) Tight for pseudo-forest edges val[u] + depth[u] t for every u not in a pseudo-tree Pseudo-forest edges remain tight, for every t Find the smallest t for which a non-pseudo-forest edge becomes tight Sum of depths increases at most n 2 iterations O(mn 2) time

Speeding-up the algorithm Do not reset the clock after each iteration The ‘time’ at which the edge (u, v) becomes tight

An O(mn+n 2 log n) algorithm We would like to use Fibonacci heaps Unfortunately, time(u, v) may increase, as well as decrease Luckily, time(u) = minv time(u, v) can only decrease The resulting algorithm is similar to the algorithm of [Young-Tarjan-Orlin ’ 91] The Running time ‘typically’ (m + n log n) ? ? ?

Discounted All-Pairs Shortest Paths a a b b c Shortest paths may be ‘infinite’ d The prefix of a shortest path is not necessarily a shortest path!

Discounted All-Pairs Shortest Paths Naïve algorithm runs in O(n 4)-time [Papadimitriou-Tsitsiklis ’ 87] A randomized O*(m 1/2 n 2)-time algorithm

Open problems ● Equivalence of non-discounted DMDPs and discounted DMDPs? ● o(mn)-time algorithms? ● Different discount factors for different edges? ● (Non-deterministic) Markov Decision Processes?

THE END