Dining Cryptographers R Newman Topics Defining anonymity Need

Dining Cryptographers R. Newman

Topics Defining anonymity Need for anonymity Defining privacy Threats to anonymity and privacy Mechanisms to provide anonymity Metrics for Anonymity Applications of anonymity technology

Dining Cryptographer Problem Three cryptographers go out for dinner They are told that the bill has been paid Benefactor wishes to remain anonymous Could be one of them, or a fourth party (e. g. , NSA) Want to know if one of them paid Respect desire to remain anonymous But want to find this piece of information

Dining Cryptographer Protocol Each pair of cryptographers flips a fair coin This is done in secret, so only the pair can see it Each cryptographer states XOR of coins States whether the pair of coins they saw were same If one paid, reports the opposite result Each computes answer Odd number of differences => a cryptographer paid Even number of difference => someone else paid

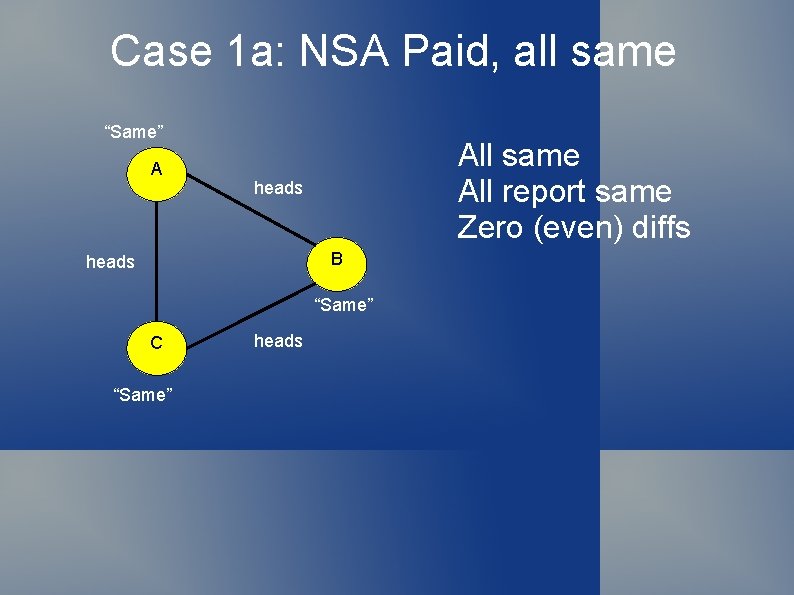
Dining Cryptographer Protocol Why does this work? Assuming all cryptographers are honest 1. First, consider case where NSA paid 1 a. All heads or all tails => no differences Even number of differences, So conclude NSA paid

Case 1 a: NSA Paid, all same “Same” A All same All report same Zero (even) diffs heads B heads “Same” C “Same” heads

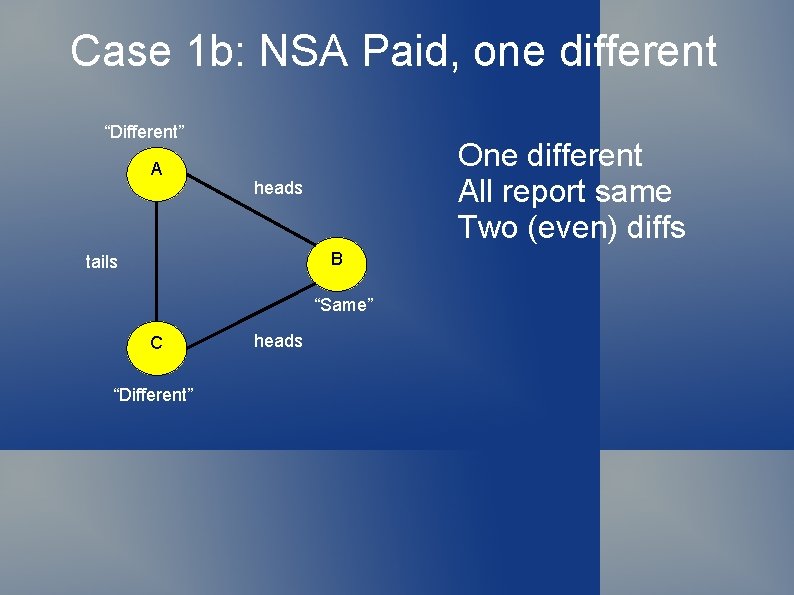
Dining Cryptographer Protocol Why does this work? Assuming all cryptographers are honest 1. First, consider case where NSA paid 1 a. All heads or all tails => no differences 1 b. Two of one and one of the other => two differences Either way, even number of differences!

Case 1 b: NSA Paid, one different “Different” A One different All report same Two (even) diffs heads B tails “Same” C “Different” heads

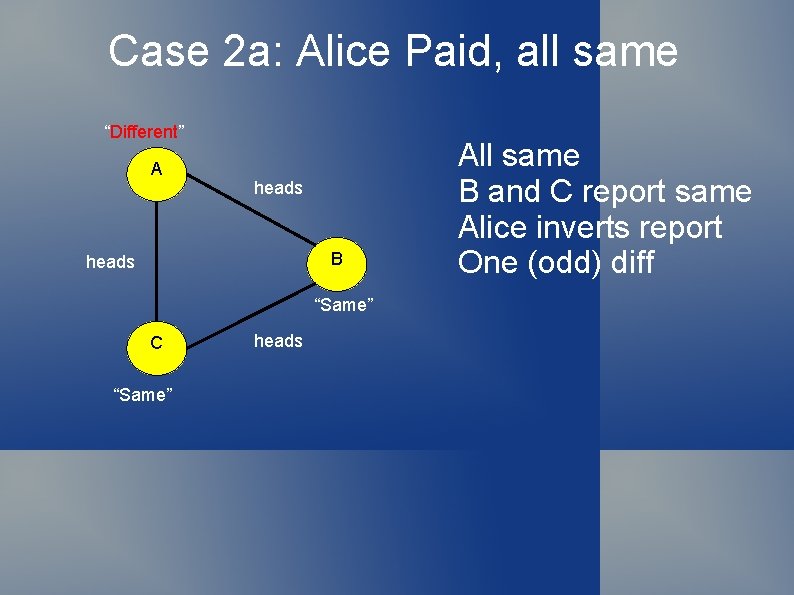
Dining Cryptographer Protocol Why does this work? Assuming all cryptographers are honest 2. Now what if one cryptographer inverts report? 2 a. All same => two say same, one says different => one difference

Case 2 a: Alice Paid, all same “Different” A heads B heads “Same” C “Same” heads All same B and C report same Alice inverts report One (odd) diff

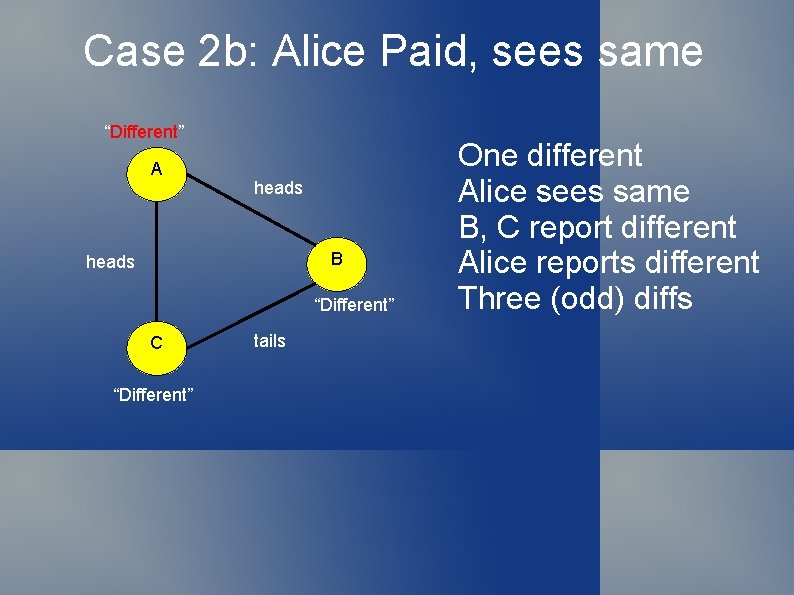
Dining Cryptographer Protocol Why does this work? Assuming all cryptographers are honest 2. Now what if one cryptographer inverts report? 2 a. All same => one difference 2 b/c. Two of one, one of other: 2 b. Payer sees equal pair => says different, and other two see different pairs, say different => 3 differences (odd)

Case 2 b: Alice Paid, sees same “Different” A heads B heads “Different” C “Different” tails One different Alice sees same B, C report different Alice reports different Three (odd) diffs

Dining Cryptographer Protocol Why does this work? Assuming all cryptographers are honest 2. Now what if one cryptographer inverts report? 2 a. All same => 1 difference 2 b/c. Two of one, one of other: 2 b. Payer sees equal pair => 3 differences 2 c. Payer sees unequal pair => says same One of the others sees equal, one sees unequal Hence 1 difference reported

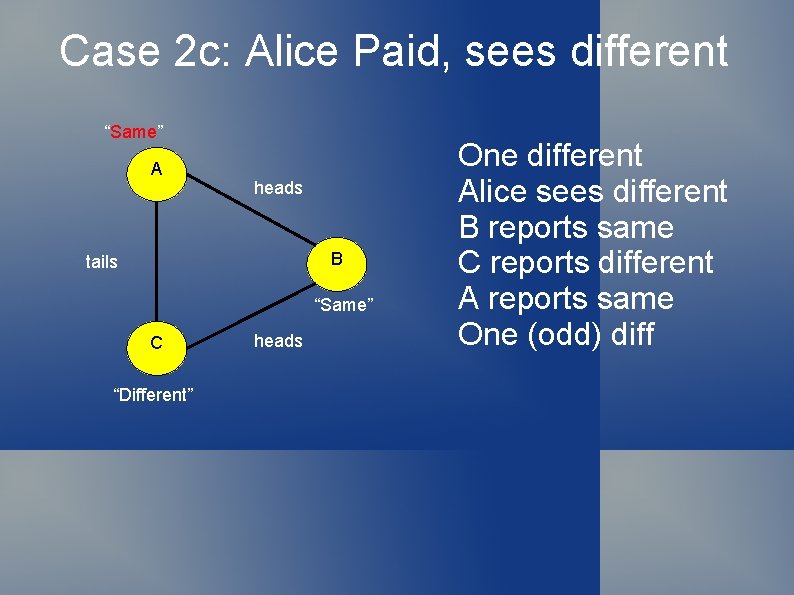
Case 2 c: Alice Paid, sees different “Same” A heads B tails “Same” C “Different” heads One different Alice sees different B reports same C reports different A reports same One (odd) diff

Dining Cryptographer Protocol Why does this work? 1. No cryptographers invert report 1 a. All heads or all tails => 0 differences 1 b. Two of one and one of the other => 2 differences Either way, even number of differences! 2. One cryptographer inverts report 2 a. All same => 1 difference 2 b/c. Two of one, one of other: 2 b. Payer sees equal pair => 3 differences 2 c. Payer sees unequal pair => 1 difference Always odd number of differences reported

Dining Cryptographer Protocol How does it preserve anonymity? View of non-paying cryptographer: If even difference, there is nothing to discover If odd difference, two cases: Cryptographer sees equal values One of the others said ”same”, other said ”different” Hidden coin is same => one who said ”different” paid Hidden coin different => one who said ”same” paid Each is equally likely! (Fair coin)

Dining Cryptographer Protocol How does it preserve anonymity? View of non-paying cryptographer: If even difference, there is nothing to discover If odd difference, two cases: Cryptographer sees unequal values Both of the others said ”different” => payer closest to coin that is same as hidden coin Both of the others said ”same” => payer closest to coin different from hidden coin Each is equally likely! (Fair coin)

Dining Cryptographer Protocol OK – so what? Now can send one bit anonymously Extend protocol to anonymously transmission Repeat protocol in rounds Each round, act like non-payer unless you have msg When you have message, start sending bits Invert report when sending 1’s, not when 0’s What about collisions? Use collision detection, backoff protocol CSMA/CD with backoff – like Ethernet!

Dining Cryptographer Protocol OK – so what? Now can send one bit anonymously For three senders Extend protocol to multiple senders Complete graph for N senders Each edge represents a fair coin Report XOR of all coins (or invert it for 1) Note that with N=2, only non-participants don’t know the sender (not secret from participants)

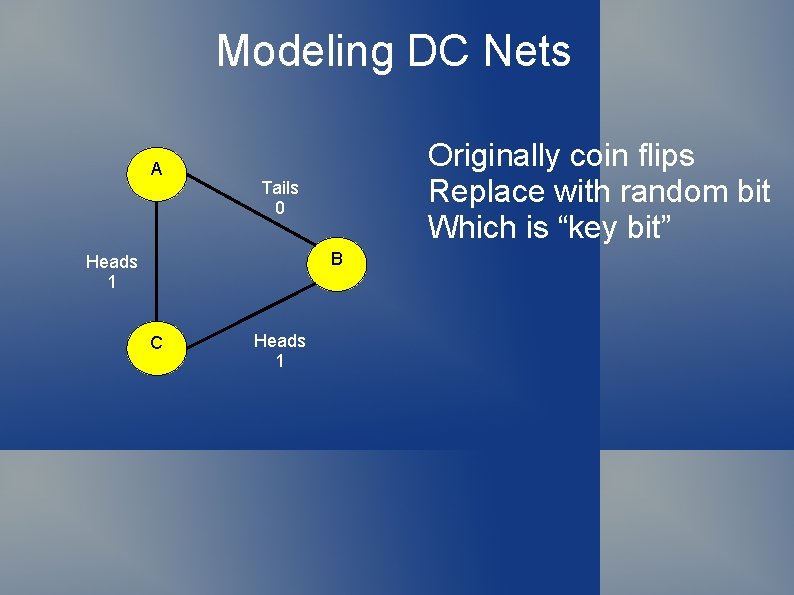
Dining Cryptographer Protocol Why does this work? Each bit appears in two sums In sum of sums, these cancel each other out If one cryptographer inverts, then odd number of sum of reports is 1, otherwise it is 0 Replace coin flips with key bits Each participant shares a key with each other participant Same number of bits in key as rounds of protocol Use key bits as coin values in protocol

Modeling DC Nets Two kinds of secret per participant: Secret pairwise keys shared with other participants Message bits Consider collusion later. . Remaining information: Which pairs share a key (not required to be secret) What each participant outputs each round Compute sum of outputs

Modeling DC Nets Model with graph: Each participant is a node Each key is represented by an edge Edge is incident on participants sharing key Graph is connected, may not be complete

Modeling DC Nets A Originally coin flips Replace with random bit Which is “key bit” Tails 0 B Heads 1 C Heads 1

Modeling DC Nets Model with graph Anonymity Set seen by a set of keys AS = Set of vertices in a connected component remaining in graph after removing edges corresponding to keys in set Two participants connected by non-compromised keys are in same AS, and are indistinguishable – only parity of report can be determined

Examples Non-participant observer All participants in same CC are in same AS (Graph remains connected after removing 0 edges) Complete key compromise All edges are removed All nodes are singletons No anonymity: Sent bit = XOR of key bits with report

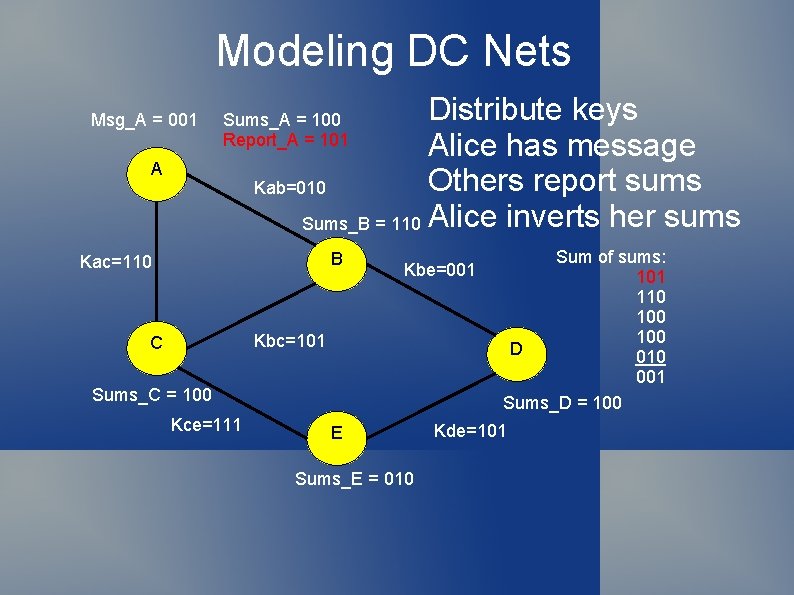
Modeling DC Nets Msg_A = 001 Distribute keys Alice has message Others report sums Kab=010 Sums_B = 110 Alice inverts her sums Sums_A = 100 Report_A = 101 A B Kac=110 Kbe=001 Kbc=101 C Sums_C = 100 Kce=111 E Sums_E = 010 Sum of sums: 101 110 100 D 010 001 Sums_D = 100 Kde=101

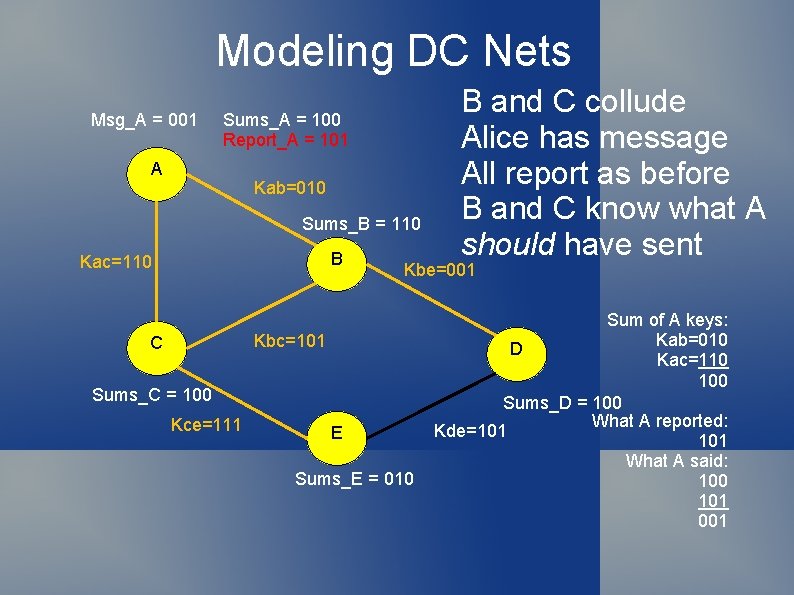
Modeling DC Nets Msg_A = 001 Sums_A = 100 Report_A = 101 A Kab=010 Sums_B = 110 B Kac=110 Kbe=001 Kbc=101 C Sums_C = 100 Kce=111 B and C collude Alice has message All report as before B and C know what A should have sent E Sums_E = 010 Sum of A keys: Kab=010 D Kac=110 100 Sums_D = 100 What A reported: Kde=101 What A said: 100 101 001

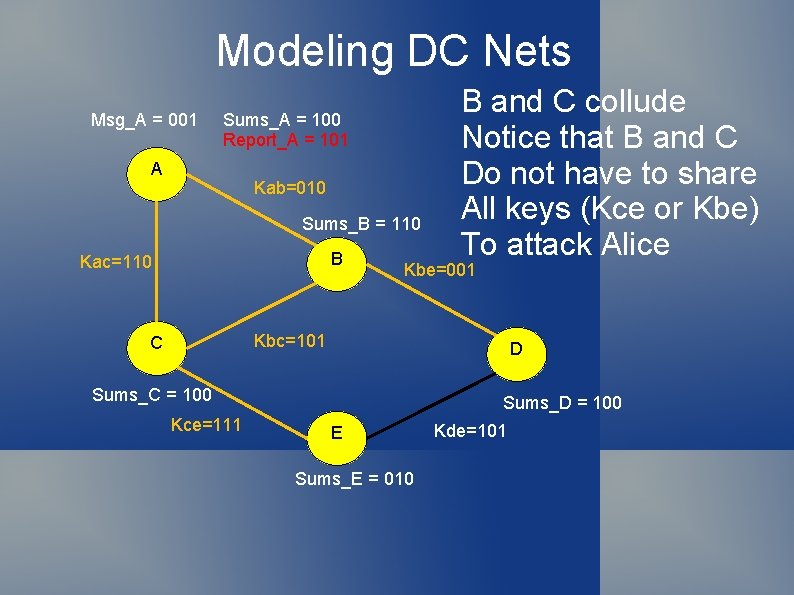
Modeling DC Nets Msg_A = 001 Sums_A = 100 Report_A = 101 A Kab=010 Sums_B = 110 B Kac=110 B and C collude Notice that B and C Do not have to share All keys (Kce or Kbe) To attack Alice Kbe=001 Kbc=101 C D Sums_C = 100 Kce=111 Sums_D = 100 E Sums_E = 010 Kde=101

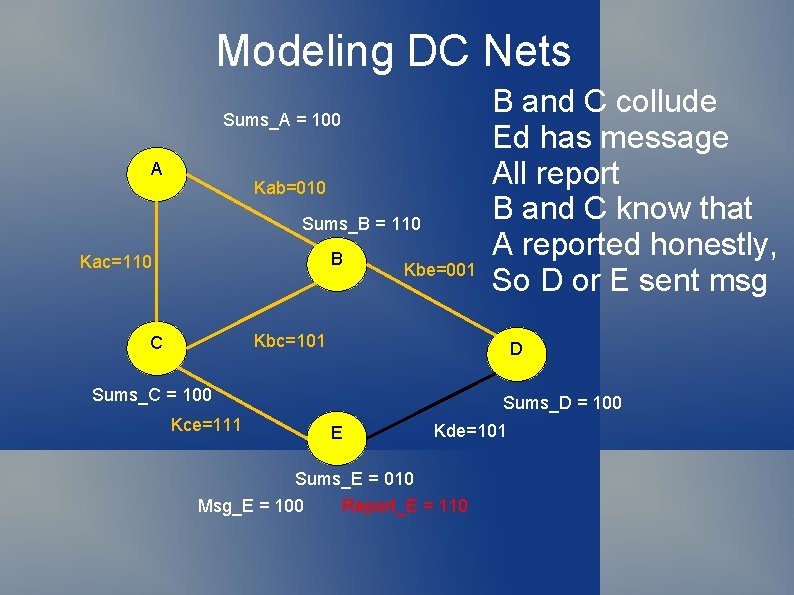
Modeling DC Nets Sums_A = 100 A Kab=010 Sums_B = 110 B Kac=110 Kbe=001 B and C collude Ed has message All report B and C know that A reported honestly, So D or E sent msg Kbc=101 C D Sums_C = 100 Kce=111 Sums_D = 100 E Kde=101 Sums_E = 010 Msg_E = 100 Report_E = 110

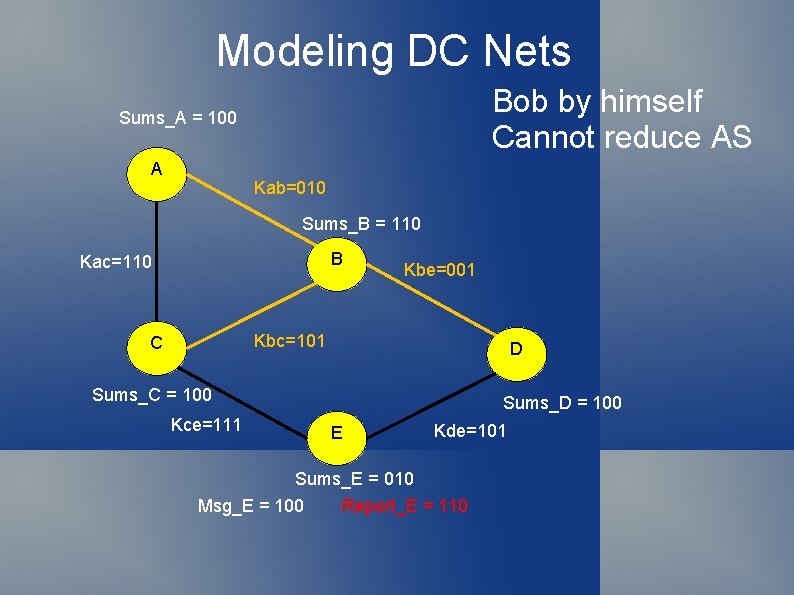
Modeling DC Nets Bob by himself Cannot reduce AS Sums_A = 100 A Kab=010 Sums_B = 110 B Kac=110 Kbe=001 Kbc=101 C D Sums_C = 100 Kce=111 Sums_D = 100 E Kde=101 Sums_E = 010 Msg_E = 100 Report_E = 110

Examples Biconnected graph All pairs of participants are connected by at least two node-disjoint paths No single participant can reduce AS size of other participants by itself Requires collusion to learn anything! All collusion buys is parity of sum of inversions of each connected component Inversions hidden by one or more key bits

Formal Model Connected component C: m nodes and n edges m x n incidence matrix M Nota bene! Stochastic variable keys K over GF(2 n) One per edge, uniform random Stochastic variable msg bits I over GF(2 m) nodes = rows and edges = columns One per vertex, uniform random A = (MK) + I = reports of the vertices Parity(A) = parity(I) since columns of M have even parity

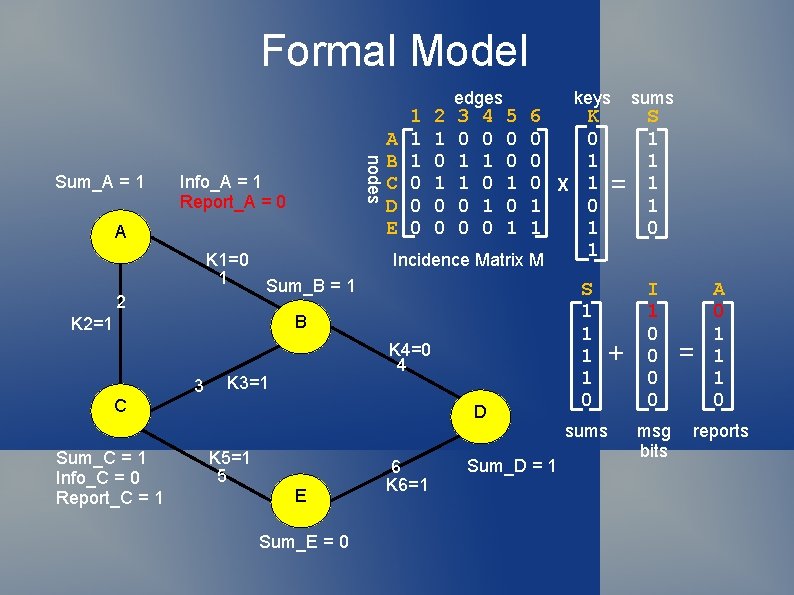
Formal Model nodes Sum_A = 1 Info_A = 1 Report_A = 0 A K 1=0 1 Sum_B = 1 2 Sum_C = 1 Info_C = 0 Report_C = 1 2 1 0 0 3 0 1 1 0 0 4 0 1 0 5 0 0 1 3 K 4=0 4 K 3=1 D K 5=1 5 E Sum_E = 0 keys 6 K A 0 0 B 0 1 C 0 X 1 D 1 0 E 1 1 1 Incidence Matrix M B K 2=1 C 1 1 1 0 0 0 edges 6 K 6=1 Sum_D = 1 S 1 1 0 sums = + S 1 1 0 I 1 0 0 msg bits = A 0 1 1 1 0 reports

Formal Model Thm: Let a be in GF(2 n). For each i in GF(2 n), which is assumed by I with non-zero probability, and which has the same parity as a, Prob(A=a | I=i) = 21 -m. hence Prob(I=i | A=a) = prob(I=i) a priori. Prf: Since every proper subset of rows of M is is linearly independent, the rank of M is m-1, and any zero parity vector in GF(2 n) can be written as a linear combination of the columns of M. So the system of linear equalities MK+i = a is solvable, since MK = a+i has zero parity. The system has exactly 2 n-m+1 solutions. Since K and I are mutually independent and K is uniformly distributed, theorem follows.

Formal Model Thm: Let a be in GF(2 n). For each i in GF(2 n), which is assumed by I with non-zero probability, and which has the same parity as a, Prob(A=a | I=i) = 21 -m. hence Prob(I=i | A=a) = prob(I=i) a priori. Prf: Since the rank of M is m-1, The system has exactly 2 n-m+1 solutions. Since K and I are mutually independent and K is uniformly distributed, theorem follows.

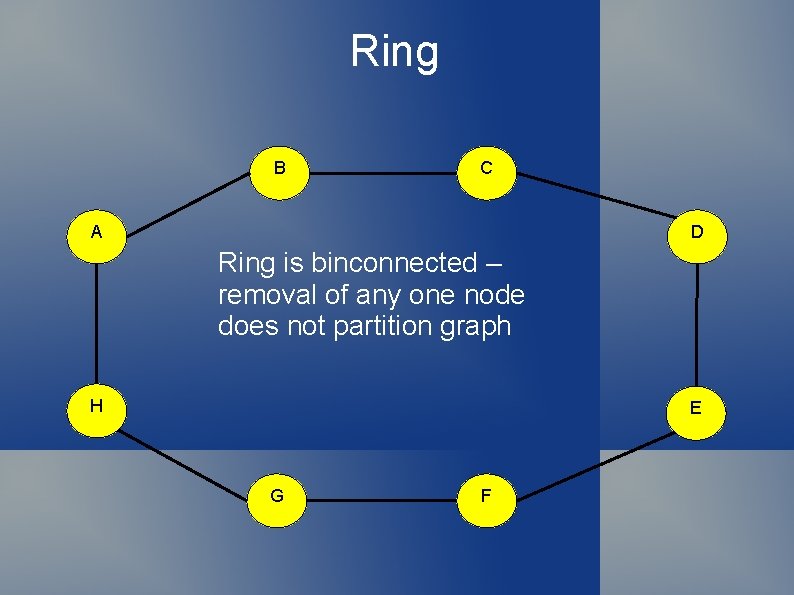
Building Graphs Complete graphs do not scale Can use a ring But any two colluders can partition ring If colluders surround a target node It is compromised!

Ring B C A D Ring is binconnected – removal of any one node does not partition graph H E G F

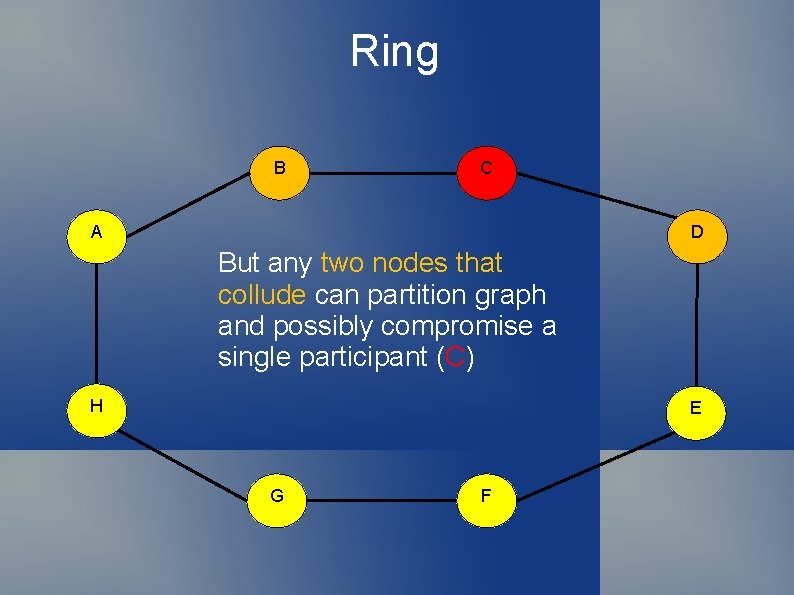
Ring B C A D But any two nodes that collude can partition graph and possibly compromise a single participant (C) H E G F

Building Graphs ”Trusted not to collude” clique – Subset of participants whom all believe will not collude Subset forms a clique All others share a key with each member of clique All members of clique must collude to compromise

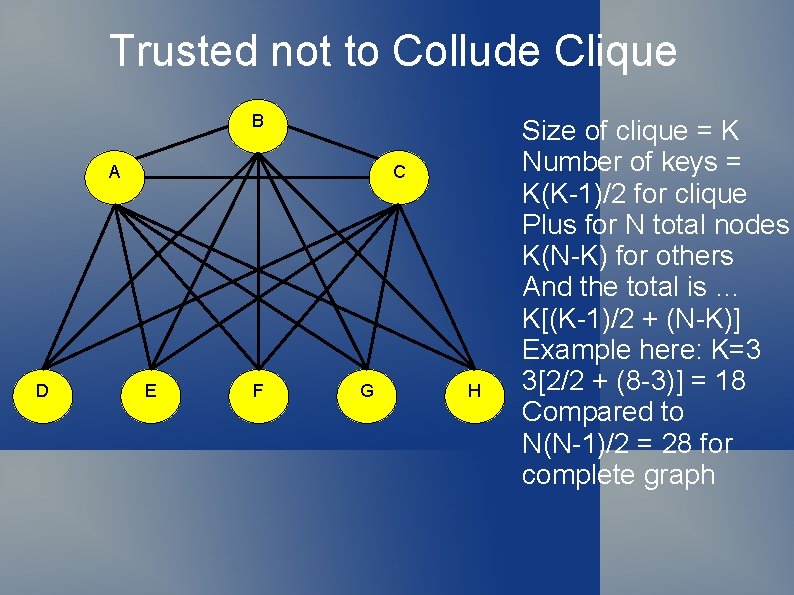
Trusted not to Collude Clique B A D C E F G H A, B, and C are mutually hostile Hence trusted not to collude They form a “root clique” All others nodes connect to each member of root clique

Trusted not to Collude Clique B A D C E F G H Size of clique = K Number of keys = K(K-1)/2 for clique Plus for N total nodes K(N-K) for others And the total is … K[(K-1)/2 + (N-K)] Example here: K=3 3[2/2 + (8 -3)] = 18 Compared to N(N-1)/2 = 28 for complete graph

Trusted not to Collude Clique B A D All members of root clique must collude to compromise any node Suppose B and C collude… C E F G H

Trusted not to Collude Clique B A D C E F G H All members of root clique must collude to compromise any node Suppose B and C collude… Then A still connects all other nodes The AS is maximal!

Preventing Disruption Well, can’t really prevent it. . . But can detect it and weed out disrupters Requires: Key-sharing graph is publically agreed on Each participant’s outputs are publically agreed on such that no participant can change their output for a round based on the other participant’s outputs for that round Some rounds contain inversions that would not compromise the untraceability of any non-disrupter

Preventing Disruption Key-sharing graph is publically agreed on Participantd can’t change outputs Distributed consensus Simultaneous broadcast channels Commitment protocols Contestable rounds that do not compromise the untraceability of any non-disrupter Slot reservation protocol

Slot Reservation Protocol Messages sent in two blocks Sender reserves one or more slots Sets corresponding bit(s) in reservation block Sends message in corresponding slots For contestable rounds, all N participants must always make one reserveration each round Reservation block with one bit per msg slot Message block with multiple message slots Requires quadratic slots due to Birthday Paradox Disrupted reservation block likely to have Hamming weight unequal to N All bits of reserving block can be safely contested

Single Disrupter If it tells the truth about shared keys bits for contested bit, or lies about an even number of key bits, it implicates itself The sum of the claimed key bit values is not what it reported (apart from allowed inversion) If it lies about an odd number. . . Values it claims will differ from values claimed by those who share the keys it lies about Casting suspicion on itself and each of them But all disputed bits point to disrupter And falsely accused participants know disrupter And can refuse to share edge with disrupter in future

Multiple Disrupters At least one inversion revealed as illegit or at least one key bit disputed Result of each contested round Since parity of outputs does not correspond to parity of legit inversions Remove at least one edge, or Remove at least one vertex from agree graph If every disruption has non-zero probability of being contested Then bounded amount of disruption possible before disrupters excluded Removed (vertex) or Share no keys (edges)

Tracing by Consent Deter antisocial use of network by. . . Allowing trace of any message by cooperation of most participants Digital signatures on shared bits can stop this Example: court orders all participants to reveal their shared key bits for a round of the message Sender may try to spread blame by lying about and odd number of shared bits Allow contested rounds to be fully resolved Allow accused senders to exonerate themselves Allow colluders to convince each other to trust them But allow sender self-incrimination: non-repudiation! Variant prevents self-incrimination

Split-bit Signatures Variant prevents self-incrimination Each participant in a pair signs a differnt bit whose sum is the actual shared bit Sharers can tell if the signatures are good Others can’t tell what bit is if one is lying Helps resolve contested rounds Contester of a bit shows signature of other party Other party must reveal contester’s signature. . . or be considered a disrupter

Compare to Mix-nets Mix-net relies on security of PKCS These are at best computationally secure DC-nets can offer unconditional security Underspecified system of equations Network load is an issue, though And maybe also symmetric crypto May not be able to handle traffic to root clique Mix-nets can also provide recipient untraceability And untraceable return addressing