Data Structures Algorithms UnionFind Example Richard Newman Steps

Data Structures & Algorithms Union-Find Example Richard Newman

Steps to Develop an Algorithm s s s s Define the problem – model it Determine constraints Find or create an algorithm to solve it Evaluate algorithm – speed, space, etc. If algorithm isn’t satisfactory, why not? Try to fix algorithm Iterate until solution found (or give up)

Dynamic Connectivity Problem • Given a set of N elements • Support two operations: • • Connect two elements Given two elements, is there a path between them?

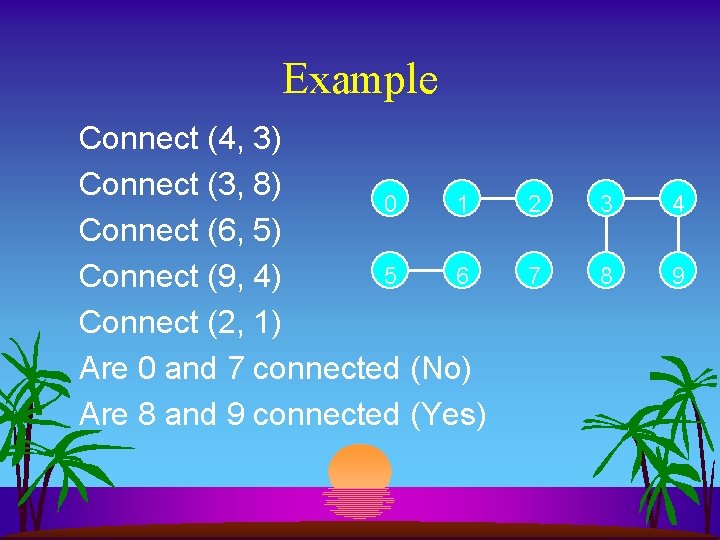
Example Connect (4, 3) Connect (3, 8) 0 1 Connect (6, 5) 5 6 Connect (9, 4) Connect (2, 1) Are 0 and 7 connected (No) Are 8 and 9 connected (Yes) 2 3 4 7 8 9

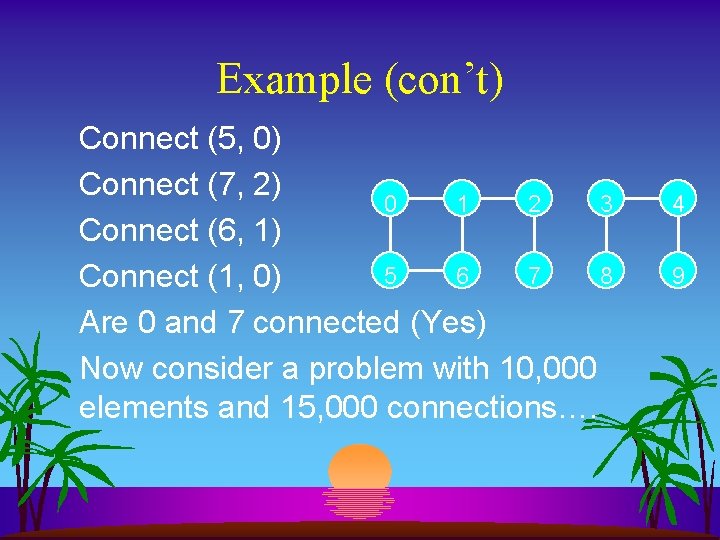
Example (con’t) Connect (5, 0) Connect (7, 2) 0 1 2 3 Connect (6, 1) 5 6 7 8 Connect (1, 0) Are 0 and 7 connected (Yes) Now consider a problem with 10, 000 elements and 15, 000 connections…. 4 9

Modeling the Elements Various interpretations of the elements: s Pixels in a digital photo s Computers in a network s Socket pins on a PC board s Transistors in a VLSI design s Variable names in a C++ program s Locations on a map s Friends in a social network s … Convenient to just number 0 to N-1 Use as array index, suppress details

Modeling the Connections Assume “is connected to” is an equivalence relation s Reflexive: a is connected to a s Symmetric: if a is connected to b, then b is connected to a s Transitive: if a is connected to b, and b is connected to c, then a is connected to c

Connected Components s A connected component is a maximal set of elements that are mutually connected (i. e. , an equivalence set) 0 1 2 3 4 5 6 7 8 9 {0} {1, 2} {3, 4, 8, 9} {5, 6} {7}

Implementing the Operations Recall – connect two elements, and answer if two elements have a path between them s Find: in which component is element a? s Union: replace components containging elements a and b with their union s Connected: are elements a and b in the same component?

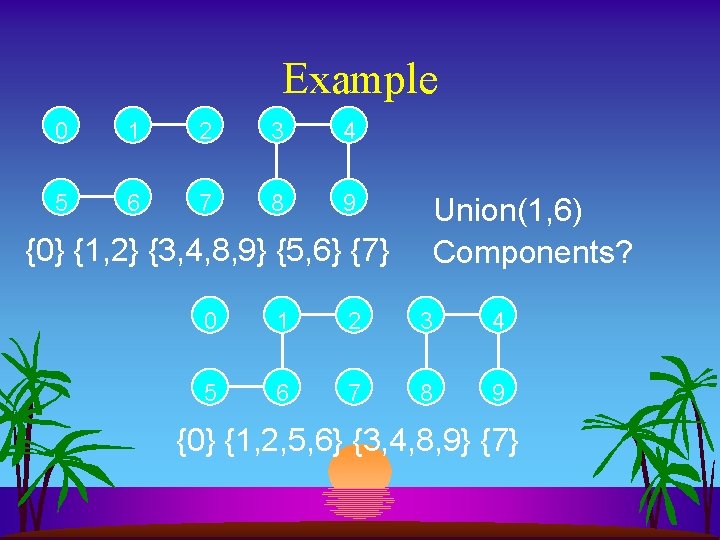
Example 0 1 2 3 4 5 6 7 8 9 {0} {1, 2} {3, 4, 8, 9} {5, 6} {7} Union(1, 6) Components? 0 1 2 3 4 5 6 7 8 9 {0} {1, 2, 5, 6} {3, 4, 8, 9} {7}

Union-Find Data Type Goal: Design an efficient data structure for union-find s Number of elements can be huge s Number of operations can be huge s Union and find operations can be intermixed public class UF UF int(N); void union(int a, int b); int find(int a); boolean connected(int a, int b);

Dynamic Connectivity Client s s Read in number of elements N from stdin Repeat: – Read in pair of integers from stdin – If not yet connected, connect them and print out pair read input int N while stdin is not empty read in pair of ints a and b if not connected (a, b) union(a, b) print out a and b

Quick-Find s Data Structure – Integer array id[] of length N – Interpretation: id[a] is the id of the component containing a i: 0 1 2 3 4 5 6 7 8 9 id[i]: 0 1 1 4 4 5 5 7 4 4 0 1 2 3 4 5 6 7 8 9

Quick-Find s Data Structure – Integer array id[] of length N – Interpretation: id[a] is the id of the component containing a s s s Find: what is the id of a? Connected: do a and b have the same id? Union: Change all the entries in id that have the same id as a to be the id of b.

Quick-Find i: 0 1 2 3 4 5 6 7 8 9 id: 0 1 1 4 4 5 5 7 4 4 0 1 2 3 4 5 6 7 8 9 Union(1, 6) i: 0 1 2 3 4 5 6 7 8 9 id: 0 5 5 4 4 5 5 7 4 4 It works – so is there a problem? Well, there may be many values to change, and many to search!

Quick-Find s Quick-Find operation times – – s Initialization takes time O(N) Union takes time O(N) Find takes time O(1) Connected takes time O(1) Union is too slow – it takes O(N 2) array accesses to process N union operations on N elements

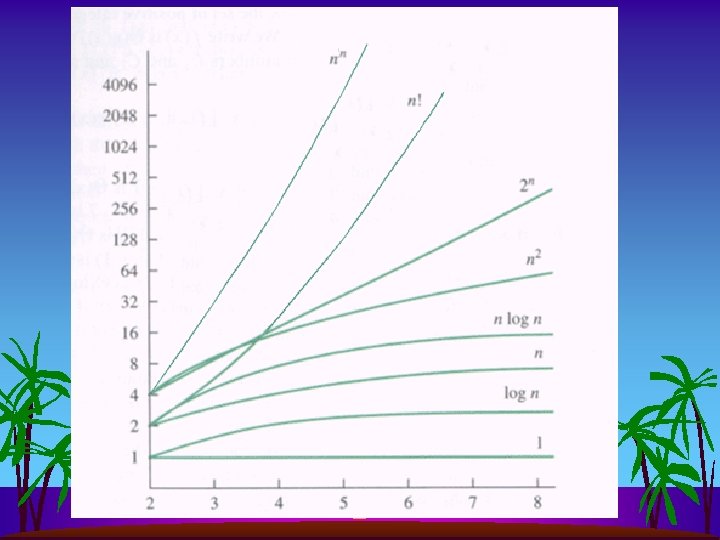
Quadratic Algos Do Not Scale! s Rough Standards (for now) – 109 operations per second – 109 words of memory – Touch all words in 1 second (+/- truism since 1950!) s Huge problem for Quick-Find: s s 109 union commands on 109 elements Takes more than 1018 operations This is 30+ years of computer time!

Quadratic Algos Do Not Scale! s They do not keep pace with technology s s s New computer may be 10 x as fast But it has 10 x as much memory Want to solve problems 10 x as big With quadratic algorithm, it takes… … 10 x as long!!!

Quick-Union s Data Structure – Integer array id[] of length N – Interpretation: id[a] is the parent of a – Component is root of a = id[id[…id[a]…]] (fixed point) i: 0 1 2 3 4 5 6 7 8 9 id[i]: 0 1 1 3 3 5 5 7 3 4 0 1 2 3 8 5 4 6 9 7

Quick-Union s Data Structure – Find: What is root of tree of a? – Connected: Do a and b have the same root? – Union: Set id of root of b’s tree to be root of a’s tree i: 0 1 2 3 4 5 6 7 8 9 id[i]: 0 1 1 3 3 5 5 7 3 4 0 1 2 3 8 5 4 6 9 7

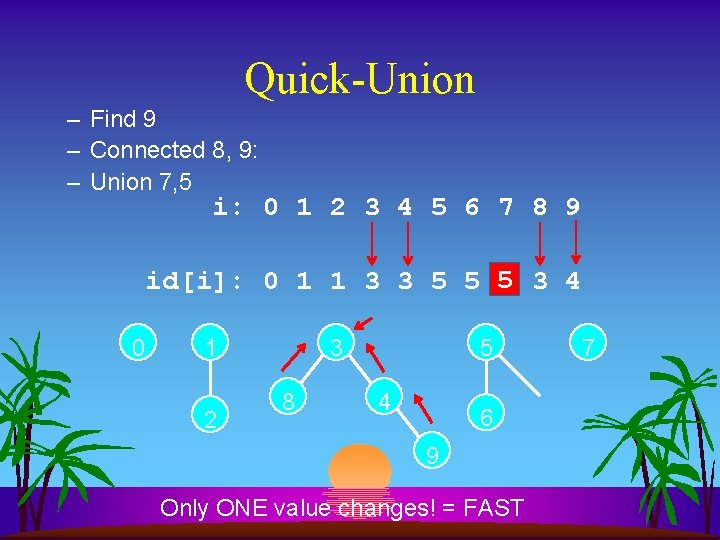
Quick-Union – Find 9 – Connected 8, 9: – Union 7, 5 i: 0 1 2 3 4 5 6 7 8 9 id[i]: 0 1 1 3 3 5 5 5 7 3 4 0 1 2 3 8 5 4 6 9 Only ONE value changes! = FAST 7

Quick-Union s Quick-Union operation times (worst case) – – s Initialization takes time O(N) Union takes time O(N) (must find two roots) Find takes time O(N) Connected takes time O(N) Now union AND find are too slow – it takes O(N 2) array accesses to process N operations on N elements

Quick-Find/Quick-Union s s Observations: Problem with Quick-Find is unions – May take N array accesses – Trees are flat, but too expensive to keep them flat! s Problem with Quick-Union – Trees may get tall – Find (and hence, connected and union) may take N array accesses

Weighted Quick-Union s s s Make Quick-Union trees stay short! Keep track of tree size Join smaller tree into larger tree – May alternatively do union by height/rank – Need to keep track of “weight” Quick-Union may do this b a But we always want this b a

Weighted Quick-Union s Weighted Quick-Union operation times – – s Initialization takes time O(N) Union takes time O(1) (given roots) Find takes time O(depth of a) Connected takes time O(max {depth of a, b}) Proposition: Depth of any node x is at most lg N Pf: What causes depth of x to increase?

Weighted Quick-Union s Proposition: Depth of any node x is at most lg N Pf: What causes depth of x to increase? Only union! And if x is in smaller tree. So x’s tree must at least double in size each time union increases x’s depth Which can happen at most lg N times. (Why? )

WQU with Path Compression s After performing find – Set parent of all nodes along path to root – Time order is the same for the find (just traverse twice) s One-pass Variant – Set every other node’s parent to it’s grandparent s No reason NOT to do this – other than a bit of laziness – Huge benefits – tree is almost flat!

WQU with Path Compression s s Theorem: Starting from an empty data structure, any sequence of M union and find operations on N elements take O(N+M lg* N) time Proof: Difficult! (lg* is number of times you have to take log to get to 1) Performance: lg* is almost constant! And, in theory, no linear time algorithm exists!

Lg* Function s N 1 2 4 16 64 K 264 K Lg* N 0 1 2 3 4 5 Performance: lg* is almost constant!

UF Summary Algorithm Worst-Case Time Quick-Find MN Quick-Union MN Weighted Quick-Union N + M lg N Path Compression N + M lg N WQU/PC N + M lg* N

Example s s s Huge problem: 1 billion nodes, 10 billion edges WQU/PC reduces time from 3000 years to 1 minute! Faster computer won’t help! – WQU/PC on cell phone in Java beats QF on supercomputer! s Better algorithm will!

Applications s Percolation – N by N grid, each space vacant or accupied – Grid percolates if top is connected to bottom by vacant spaces – For large N, vacancy percentage for percolation is about 0. 6, known by simulation s Models – Electrical systems – Fluid flow – Social networks

Next – Lecture 3 s s Read Chapter 2 Empirical analysis Asymptotic analysis of algorithms Basic recurrences