Digital Lessons on Factoring Copyright 2007 Pearson Education

Digital Lessons on Factoring Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Factoring using the Greatest Common Factor and Factoring by Grouping 1. List all possible factors for a given number. 2. Find the greatest common factor of a set of numbers or monomials. 3. Write a polynomial as a product of a monomial GCF and a polynomial. 4. Factor by grouping. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Factored form: We say that a number or expression is in its factored form if it is written as a product of factors. Following are some examples of factored form: An integer written in factored form with integer factors: 28 = 2 • 14 A monomial written in factored form with monomial factors: 8 x 5 = 4 x 2 • 2 x 3 A polynomial written in factored form with a monomial factor and a polynomial factor: 2 x + 8 = 2(x + 4) A polynomial written in factored form with two polynomial factors: x 2 + 5 x + 6 = (x + 2)(x + 3) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 3

Listing all possible factors for a given number. Example: List all natural number factors of 24. Solution: To list all the natural number factors, we can divide 24 by 1, 2, 3, and so on, writing each divisor and quotient pair as a product until we have all possible combinations. 1 • 24, 2 • 12, 3 • 8, 4 • 6 The natural number factors of 24 are 1, 2, 3, 4, 6, 8, 12 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 4

Find the greatest common factor of a set of numbers or monomials. Greatest common factor (GCF) is the largest natural number that divides all given numbers perfectly or without remainder. Steps for finding the GCF of a set of numbers by listing: 1. List all possible factors for each given number. 2. Search the lists for the largest factor common to all lists. Example: Find the GCF of 24 and 36. Solution: Factors of 24: 1, 2, 3, 4, 6, 8, 12 Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18 The GCF of 24 and 36 is 12. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 5

Prime Factorization Method for Finding GCF To find the greatest common factor of a given set of numbers: 1. Write the prime factorization of each given number in exponential form. 2. Create a factorization for the GCF that includes only those prime factors common to all the factorizations, each raised to its smallest exponent in the factorization. 3. Multiply the factors in the factorization created in Step 2. Note: If there are no common prime factors, then the GCF is 1. Example: Find the GCF of 25 a 3 b and 40 a 2. Solution: Write the prime factorization of each monomial, treating the variables like prime factors. 25 a 3 b = 5 • a 3 • b 40 a 2 = 2 • 2 • 5 • a 2 GCF = 5 • a 2 = 5 a 2 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 6

Factoring a Monomial GCF Out of a Polynomial To factor a monomial GCF out of a given polynomial: 1. Find the GCF of the terms that make up the polynomial. 2. Rewrite the given polynomial as a product of the GCF and parentheses that contain the result of dividing the given polynomial by the GCF. Given polynomial = GCF Example: Factor: Solution Find the GCF of Because the first term in the polynomial is negative, we will factor out the negative of the GCF to avoid a negative first term inside the parentheses. We will factor out 3 x 2 y. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 7

continued 2. Write the given polynomial as the product of the GCF and the parentheses containing the quotient of the given polynomial and the GCF. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 8

Example Factor. Solution: Notice that this expression is a sum of two products, a and (b + 5), and 8 and (b + 5). Further, note that (b + 5) is the GCF of the two products. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 9

Factoring by grouping. To factor a four-term polynomial by grouping: 1. Factor out any monomial GCF (other than 1) that is common to all four terms. 2. Group together pairs of terms and factor the GCF out of each pair. 3. If there is a common binomial factor, then factor it out. 4. If there is no common binomial factor, then interchange the middle two terms and repeat the process. If there is still no common binomial factor, then the polynomial cannot be factored by grouping. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 10

Example Factor. Solution: First we look for a monomial GCF (other than 1). This polynomial does not have one. Because the polynomial has four terms, we now try to factor by grouping. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 11

Factoring Trinomials of the Form x 2 + bx + c To factor a trinomial of the form x 2 + bx + c : 1. Find two numbers with a product equal to c and a sum equal to b. 2. The factored trinomial will have the form: (x + first number) (x + second number). Note: The signs in the binomial factors can be minus signs, depending on the signs of b and c. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Example Factor. x 2 – 6 x + 8 Solution: We must find a pair of numbers whose product is 8 and whose sum is – 6. If two numbers have a positive product and negative sum, they must both be negative. Following is a table listing the products and sums: Product Sum (– 1)(– 8) = 8 – 1 + (– 8) = – 9 (– 2)(– 4) = 8 – 2 + (– 4) = – 6 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley This is the correct combination. 13

continued Answer x 2 – 6 x + 8 = (x – 2)(x – 4) Check We can check by multiplying the binomial factors to see if their product is the original polynomial. (x – 2)(x – 4) = x 2 – 4 x – 2 x + 8 = x 2 – 6 x + 8 Multiply the factors using FOIL. The product is the original polynomial. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 14

Example Factor. a 2 – ab – 20 b 2 Solution: We must find a pair of terms whose product is 20 b 2 and whose sum is – 1 b. These terms would have to be – 5 b and 4 b. Answer a 2 – ab – 20 b 2 = (a – 5 b)(a + 4 b) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 15

Factor out a monomial GCF, then factor the trinomial of the form x 2 + bx + c. Example: Factor. 4 xy 3 + 12 xy 2 – 72 xy Solution First, we look for a monomial GCF (other than 1). Notice that the GCF of the terms is 4 xy. Factoring out the monomial, we have 4 xy 3 + 12 xy 2 – 72 xy = 4 xy(y 2 + 3 y – 18) Now try to factor the trinomial to two binomials. We must find a pair of numbers whose product is – 18 and whose sum is 3. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 16

continued Product Sum (– 1)(18) = – 18 – 1 + 18 = 17 (– 2)(9) = – 18 – 2 + 9 = 7 (– 3)(6) = – 18 – 3 + 6 = 3 This is the correct combination. Answer 4 xy 3 + 12 xy 2 – 72 xy = 4 xy(y – 3)(y + 6) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 17

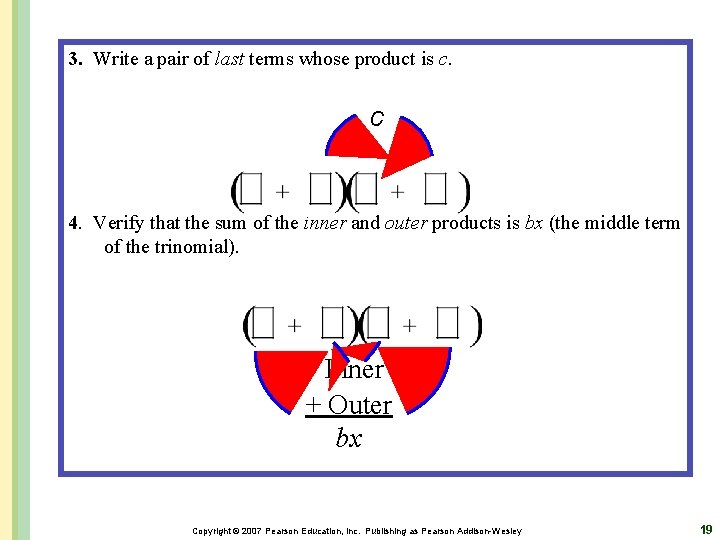
Factoring Trinomials of the Form ax 2 + bx + c, where a 1 Factoring by Trial and Error To factor a trinomial of the form ax 2 + bx + c, where a 1, by trial and error: 1. Look for a monomial GCF in all the terms. If there is one, factor it out. 2. Write a pair of first terms whose product is ax 2 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

3. Write a pair of last terms whose product is c. c 4. Verify that the sum of the inner and outer products is bx (the middle term of the trinomial). Inner + Outer bx Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 19

If the sum of the inner and outer products is not bx, then try the following: a. Exchange the first terms of the binomials from step 3, then repeat step 4. b. Exchange the last terms of the binomials from step 3, then repeat step 4. c. Repeat steps 2 – 4 with a different combination of first and last terms. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 20

Example Factor. Solution The first terms must multiply to equal 6 x 2. These could be x and 6 x, or 2 x and 3 x. The last terms must multiply to equal – 5. Because – 5 is negative, the last terms in the binomials must have different signs. This factor pair must be 1 and 5. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 21

continued Now we multiply binomials with various combinations of these first and last terms until we find a combination whose inner and outer products combine to equal 13 x. Incorrect combinations. Correct combination. Answer Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 22

Example Factor. Solution First, we factor out the monomial GCF, 3 x. Now we factor the trinomial within the parentheses. The first terms must multiply to equal 7 x 2. These could be x and 7 x. The last terms must multiply to equal 3. Because 3 is a prime number, its factors are 1 and 3. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 23

continued Now we multiply binomials with various combinations of these first and last terms until we find a combination whose inner and outer products combine to equal – 20 x. Correct combination. Answer Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 24

Factoring ax 2 + bx + c, where a 1, by Grouping To factor a trinomial of the form ax 2 + bx + c, where a 1, by grouping: 1. 2. 3. 4. Look for a monomial GCF in all the terms. If there is one, factor it out. Multiply a and c. Find two factors of this product whose sum is b. Write a four-term polynomial in which bx is written as the sum of two like terms whose coefficients are the two factors you found in step 3. 5. Factor by grouping. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 25

Example Factor. Solution Notice that for this trinomial, a = 2, b = – 15, and c = 7. We begin my multiplying a and c: (2)(7) = 14. Now we find two factors of 14 whose sum is – 15. Notice that these two factors must both be negative. Factors of ac Sum of Factors of ac (– 2)(– 7) = 14 – 2 + (– 7) = – 9 (– 1)(– 14) = 14 – 1 + (– 14) = – 15 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley Correct 26

continued – 15 x –x – 14 x Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 27

Factoring Special Products 1. 2. 3. 4. Factor perfect square trinomials. Factor a difference of squares. Factor a difference of cubes. Factor a sum of cubes. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Factoring Perfect Square Trinomials a 2 + 2 ab + b 2 = (a + b)2 a 2 – 2 ab + b 2 = (a – b)2 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 29

Example Factor. 9 a 2 + 6 a + 1 Solution This trinomial is a perfect square because the first and the last terms are perfect squares and twice the product of their roots is the middle term. 9 a 2 + 6 a + 1 The square root of 9 a 2 is 3 a. The square root of 1 is 1. Twice the product of 3 a and 1 is (2)(3 a)(1) = 6 a, which is the middle term. Answer 9 a 2 + 6 a + 1 = (3 a + 1)2 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 30

Example Factor. 16 x 2 – 56 x + 49 Solution This trinomial is a perfect square. 16 x 2 – 56 x + 49 The square root of 16 x 2 is 4 x. The square root of 49 is 7. Twice the product of 4 x and 7 is (2)(4 x)(7) = 56 x, which is the middle term. Answer 16 x 2 – 56 x + 49 = (4 x – 7)2 Use a 2 – 2 ab + b 2 = (a – b)2, where a = 4 x and b = 7. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 31

Factoring a Difference of Squares a 2 – b 2 = (a + b)(a – b) Warning: A sum of squares a 2 + b 2 is prime and cannot be factored. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 32

Example Factor. 9 x 2 – 16 y 2 Solution This binomial is a difference of squares because 9 x 2 – 16 y 2 = (3 x)2 – (4 y)2. To factor it, we use the rule a 2 – b 2 = (a + b)(a – b) 9 x 2 – 16 y 2 = (3 x)2 – (4 y)2 = (3 x + 4 y)(3 x – 4 y) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 33

Example Factor. n 4 – 625 Solution This binomial is a difference of squares, where a = n 2 and b = 25. n 4 – 625 = (n 2 + 25)(n 2 – 25) Use a 2 – b 2 = (a + b)(a – b). = (n 2 + 25)(n + 5)(n – 5) Factor n 2 – 25, using a 2 – b 2 = (a + b)(a – b) with a = n and b = 5. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 34

Factoring a Difference of Cubes a 3 – b 3 = (a – b)(a 2 + ab + b 2) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 35

Example Factor. 216 x 3 – 64 Solution This binomial is a difference of cubes. a 3 – b 3 = (a – b) (a 2 + a b + b 2) 216 x 3 – 64 = (6 x)3 – (4)3 = (6 x – 4)((6 x)2 + (6 x)(4) + (4)2) = (6 x – 4)(36 x 2 + 24 x + 16) Note: The trinomial may seem like a perfect square. However, to be a perfect square, the middle term should be 2 ab. In this trinomial, we only have ab, so it cannot be factored. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 36

Factoring a Sum of Cubes a 3 + b 3 = (a + b)(a 2 – ab + b 2) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 37

Example Factor. 6 x +162 xy 3 Solution The terms in this binomial have a monomial GCF, 6 x. 6 x +162 xy 3 = 6 x(1 + 27 y 3) = 6 x(1 + 3 y)((1)2 – (1)(3 y) + (3 y)2) = 6 x(1 + 3 y)(1 – 3 y + 9 y 2) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 38

Strategies for Factoring Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Factoring a Polynomial To factor a polynomial, first factor out any monomial GCF, then consider the number of terms in the polynomial. If the polynomial has: I. Four terms, then try to factor by grouping II. Three terms, then determine if the trinomial is a perfect square or not. A. If the trinomial is a perfect square, then consider its form. 1. If in the form a 2 + 2 ab + b 2, then the factored form is (a + b)2. 2. If in the form a 2 2 ab + b 2, then the factored form is (a b)2. B. If the trinomial is not a perfect square, then consider its form. 1. If in the form x 2 + bx + c, then find two factors of c whose sum is b, and write the factored form as (x + first number)(x + second number). Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 40

Factoring a Polynomial continued 2. If in the form ax 2 + bx + c, where a 1, then use trial and error. Or, find two factors of ac whose sum is b; write these factors as coefficients of two like terms that, when combined, equal bx; and then factor by grouping. III. Two terms, then determine if the binomial is a difference of squares, sum of cubes, or difference of cubes. A. If given a binomial that is a difference of squares, a 2 – b 2, then the factors are conjugates and the factored form is (a + b)(a – b). Note that a sum of squares cannot be factored. B. If given a binomial that is a sum of cubes, a 3 + b 3, then the factored form is (a + b)(a 2 – ab + b 2). C. If given a binomial that is a difference of cubes, a 3 – b 3, then the factored form is (a – b)(a 2 + ab + b 2). Note: Always look to see if any of the factors can be factored. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 41

Example Factor. 12 x 2 – 8 x – 15 Solution There is no GCF. Not a perfect square, since the first and last terms are not perfect squares. Use trial and error or grouping. (x – 3)(12 x + 5) = 12 x 2 + 5 x – 36 x – 15 No (6 x – 3)(2 x + 3) = 12 x 2 + 18 x – 6 x – 9 No (6 x + 5)(2 x – 3) = 12 x 2 – 18 x + 10 x – 15 = 12 x 2 – 8 x – 15 Correct Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 42

Example Factor. 5 x 3 – 10 x 2 – 120 x Solution 5 x(x 2 – 2 x – 24) Factored out the monomial GCF, 5 x. Look for two numbers whose product is – 24 and whose sum is 2. Product ( 1)(24) = 24 4( 6) = 24 Sum 1 + 24 = 23 4 + ( 6) = 2 Correct combination. 5 x 3 – 10 x 2 – 120 x =5 x(x + 4)(x – 6) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 43

Example 4 Factor. 8 a – 72 n 2 Solution 8 a 4 – 72 n 2 = 8(a 4 – 9 n 2) Factor out the monomial GCF, 8. a 4 – 9 n 2 is a difference of squares = 8(a 2 – 3 n)(a 2 + 3 n) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 44

Example Factor. 12 y 5 + 84 y 3 Solution 12 y 3(y 2 + 7) Factor out the monomial GCF, 12 y 3. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 45

Example Factor. 150 x 3 y – 120 x 2 y 2 + 24 xy 3 Solution 6 xy(25 x 2 – 20 xy + 4 y 2) Factor out the monomial GCF, 6 xy(5 x – 2 y)2 Factor the perfect square trinomial. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 46

Example Factor. x 5 – 2 x 3 – 27 x 2 + 54 Solution No common monomial, factor by grouping. (x 5 – 2 x 3)(– 27 x 2 + 54) x 3(x 2 – 2)– 27(x 2 – 2)(x 3 – 27) Difference of cubes (x 2 – 2)(x – 3)(x 2 + 3 x + 9) Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 47

Solving Quadratic Equations by Factoring . Zero-Factor Theorem If a and b are real numbers and ab = 0, then a = 0 or b = 0. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley

Solve. (x + 4)(x + 5) = 0 Example Solution According to the zero-factor theorem, one of the two factors, or both factors, must equal 0. x+4=0 or x + 5 = 0 Solve each equation. x = 4 x = 5 Check For x = 4: For x = 5: (x + 4)(x + 5) = 0 ( 4 + 4)( 4 + 1) = 0 ( 5 + 4)( 5 + 5) = 0 0( 3) = 0 ( 1)(0) = 0 Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 49

Solving Equations with Two or More Factors Equal to 0 To solve an equation in which two or more factors are equal to 0, use the zero-factor theorem: 1. Set each factor equal to zero. 2. Solve each of those equations. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 50

Example Solve. a. y(5 y + 2) = 0 Solution a. y(5 y + 2) = 0 y = 0 or 5 y + 2 = 0 5 y = 2 b. x(x + 2)(5 x – 4) = 0 b. This equation is already solved. To check, we verify that the solutions satisfy the original equations. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 51

Solve quadratic equations by factoring. Quadratic equation in one variable: An equation that can be written in the form ax 2 + bx + c = 0, where a, b, and c are all real numbers and a 0. Solving Quadratic Equations Using Factoring To solve a quadratic equation: 1. Write the equation in standard form (ax 2 + bx + c = 0). 2. Write the variable expression in factored form. 3. Use the zero-factor theorem to solve. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 52

Example Solve. 2 x 2 – 5 x – 3 = 0 Solution The equation is in standard form, so we can factor. 2 x 2 – 5 x – 3 = 0 (2 x + 1)(x – 3) = 0 Use the zero-factor theorem to solve. 2 x + 1 = 0 or x – 3 = 0 To check, we verify that the solutions satisfy the original equations. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 53

Example Solve. 6 y 2 + 11 y = 10 + 4 y Solution Write the equation in standard form. 6 y 2 + 11 y = 10 + 4 y 6 y 2 + 7 y = 10 Subtract 4 y from both sides. 6 y 2 + 7 y – 10 = 0 Subtract 10 from both sides. (6 y – 5)(y + 2) = 0 Factor. 6 y – 5 = 0 or y + 2 = 0 Use the zero-factor theorem. Copyright © 2007 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 54