Design Space Exploration for PowerEfficient MixedRadix Ling Adders

Design Space Exploration for Power-Efficient Mixed-Radix Ling Adders Chung-Kuan Cheng Computer Science and Engineering Depart. University of California, San Diego 1

Outline n Prefix Adder Problem n n n Our Work n n n Background & Previous Work Extensions: High-radix, Ling Area/Timing/Power Models Mixed-Radix (2, 3, 4) Adders ILP Formulation Experimental Results Future Work 2

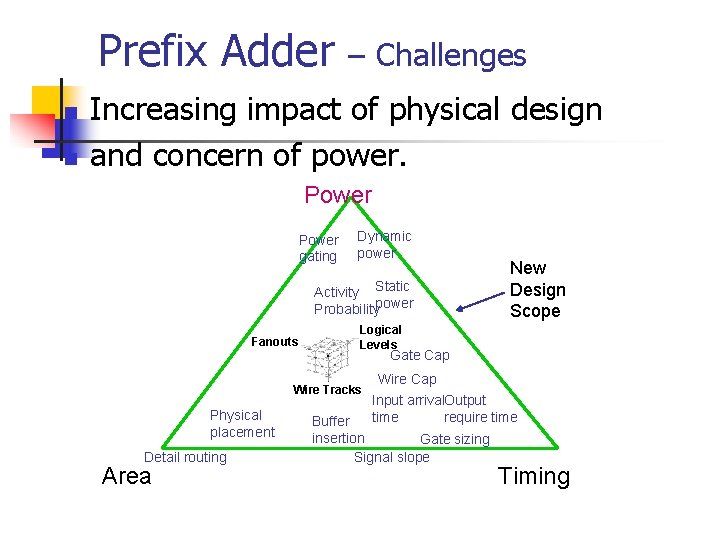
Prefix Adder n n – Challenges Increasing impact of physical design and concern of power. Power gating Dynamic power Activity Static Probabilitypower Fanouts Logical Levels Gate Cap Wire Tracks Physical placement Detail routing Area New Design Scope Wire Cap Input arrival. Output time require time Buffer insertion Gate sizing Signal slope Timing

Binary Addition n Input: two n-bit binary numbers and , one bit carry-in Output: n-bit sum and one bit carry out Prefix Addition: Carry generation & propagation 4

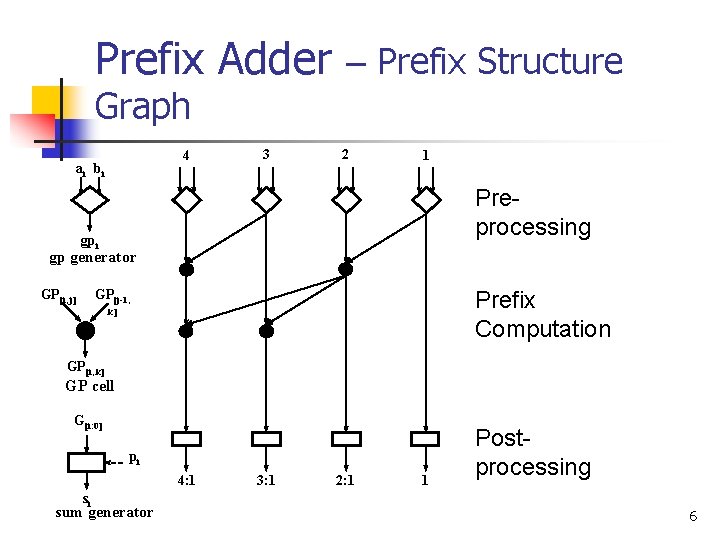
Prefix Addition – Formulation Preprocessing: Prefix Computation: Postprocessing: 5

Prefix Adder – Prefix Structure Graph 4 ai bi 3 2 1 Preprocessing gpi gp generator GP[i, j] Prefix Computation GP[j-1, k] GP[i, k] GP cell G[i: 0] pi 4: 1 si sum generator 3: 1 2: 1 1 Postprocessing 6

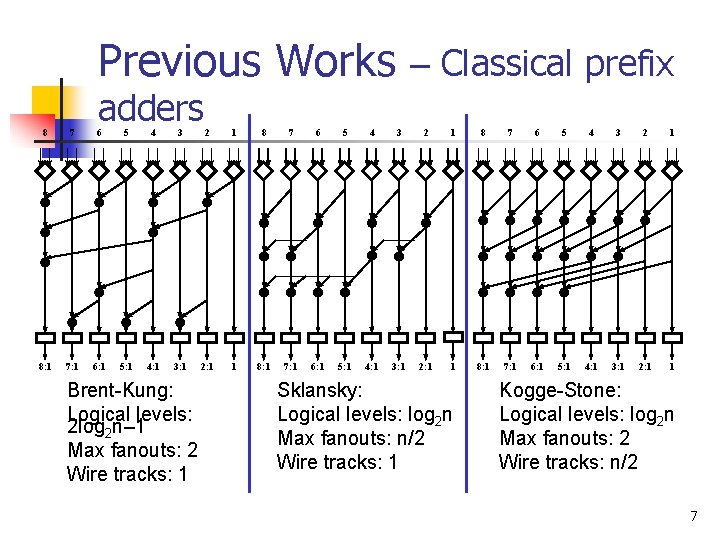
Previous Works – Classical prefix adders 8 7 6 5 4 3 2 1 8: 1 7: 1 6: 1 5: 1 4: 1 3: 1 2: 1 1 Brent-Kung: Logical levels: 2 log 2 n– 1 Max fanouts: 2 Wire tracks: 1 Sklansky: Logical levels: log 2 n Max fanouts: n/2 Wire tracks: 1 Kogge-Stone: Logical levels: log 2 n Max fanouts: 2 Wire tracks: n/2 7

High-Radix Adders n n Each cell has more than two fan-in’s Pros: less logic levels n n 6 levels (radix-2) vs. 3 levels (radix-4) for 64 -bit addition Cons: larger delay and power in each cell 8

Radix-3 Sklansky & Kogge. Stone Adder David Harris, “Logical Effort of Higher Valency Adders” 9

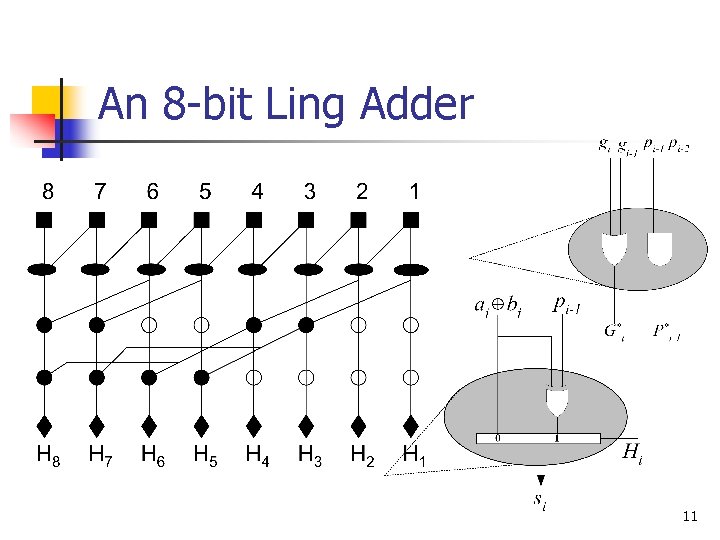
Ling Adders Prefix Ling Preprocessing: Prefix Computation: Postprocessing: 10

An 8 -bit Ling Adder 11

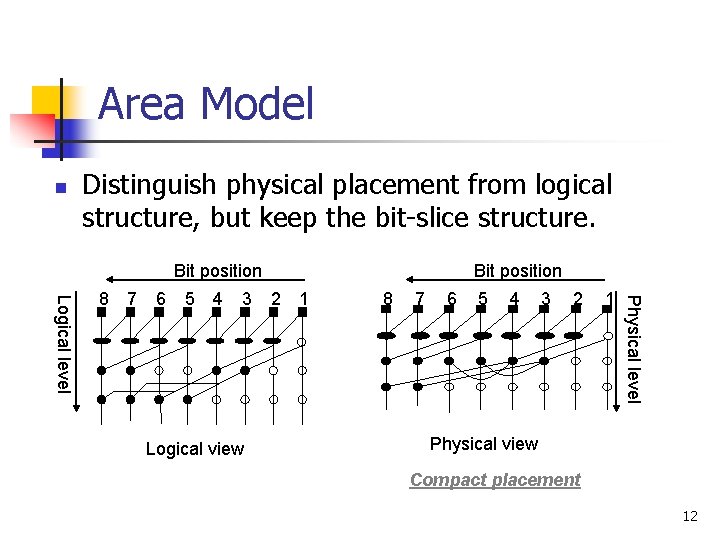
Area Model n Distinguish physical placement from logical structure, but keep the bit-slice structure. Bit position 7 6 5 4 3 Logical view 2 1 8 7 6 5 4 3 2 1 Physical level Logical level 8 Bit position Physical view Compact placement 12

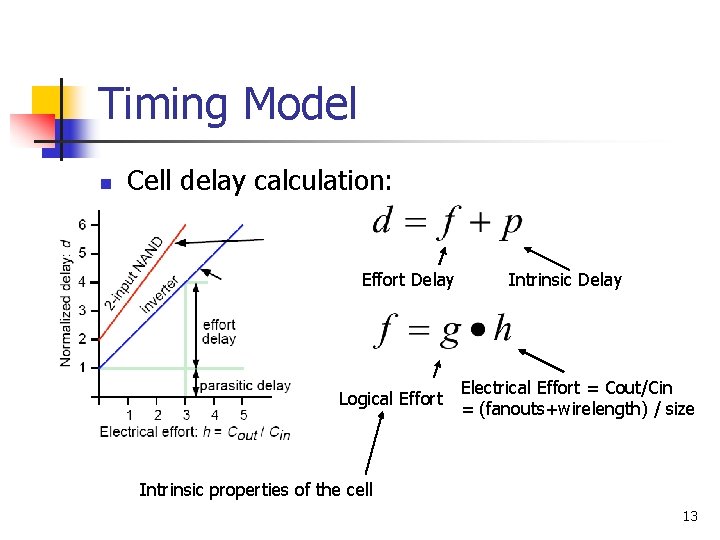
Timing Model n Cell delay calculation: Effort Delay Logical Effort Intrinsic Delay Electrical Effort = Cout/Cin = (fanouts+wirelength) / size Intrinsic properties of the cell 13

Power Model n Total power consumption: Dynamic power + Static Power n Static power: leakage current of device Psta = *#cells n Dynamic power: current switching capacitance Pdyn = Cload n is the switching probability = j (j is the logical level*) * Vanichayobon S, etc, “Power-speed Trade-off in Parallel Prefix Circuits” 14

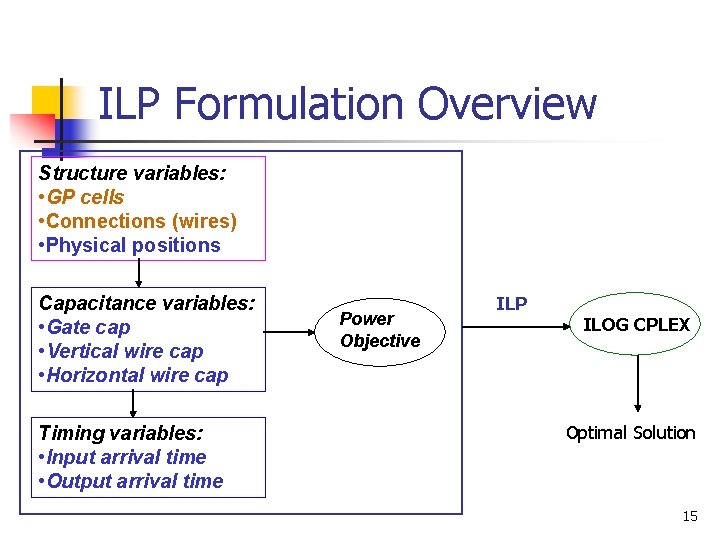
ILP Formulation Overview Structure variables: • GP cells • Connections (wires) • Physical positions Capacitance variables: • Gate cap • Vertical wire cap • Horizontal wire cap Timing variables: • Input arrival time • Output arrival time Power Objective ILP ILOG CPLEX Optimal Solution 15

Integer Linear Programming (ILP) n n ILP: Linear Programming with integer variables. Difficulties and techniques: n Constraints are not linear n n Search Space too large n n Linearize using pseudo linear constraints Reduce search space Search is slow n Add redundant constraints to speedup 16

ILP – Integer Linear Programming n n Linear Programming: linear constraints, linear objective, fractional variables. Integer Linear Programming: Linear Programming with integer variables. Constraints LP Optimal ILP Optimal 17

ILP – Pseudo-Linear Constraint • A constraint is called pseudo-linear if it’s not effective until some integer variables are fixed. Problem: Minimize: x 3 Subject to: x 1 300 x 2 500 x 3 = min(x 1, x 2) LP objective: 0 ILP objective: 300 ILP formulation: Minimize: x 3 Subject to: x 1 300 x 2 500 x 3 x 1 x 3 x 2 x 3 x 1 – 1000 b 1 x 3 x 2 – 1000 (1 – b 1) b 1 is binary (1) (2) • Pseudo-linear constraints mostly arise from IF/ELSE scenarios • binary decision variables are introduced to indicate true or false.

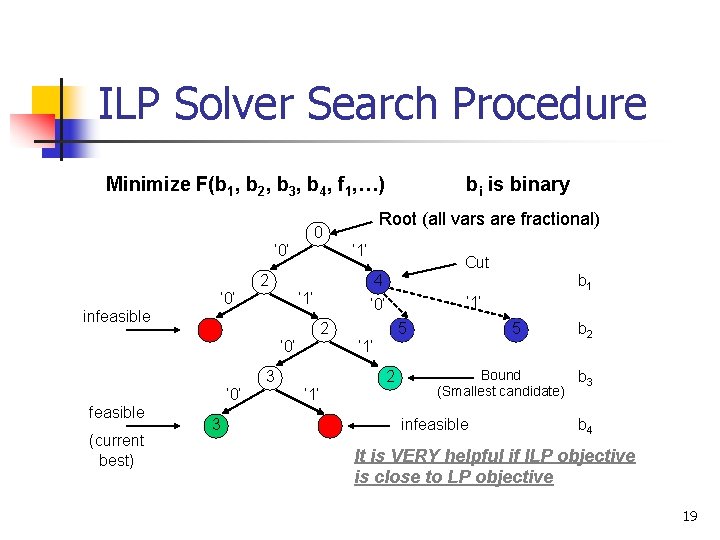
ILP Solver Search Procedure Minimize F(b 1, b 2, b 3, b 4, f 1, …) Root (all vars are fractional) 0 ‘ 0’ ‘ 1’ 2 ‘ 0’ (current best) 3 b 1 ‘ 1’ 5 5 ‘ 1’ 3 feasible Cut 4 ‘ 0’ ‘ 1’ infeasible bi is binary 2 ‘ 1’ b 2 Bound b 3 (Smallest candidate) infeasible b 4 It is VERY helpful if ILP objective is close to LP objective 19

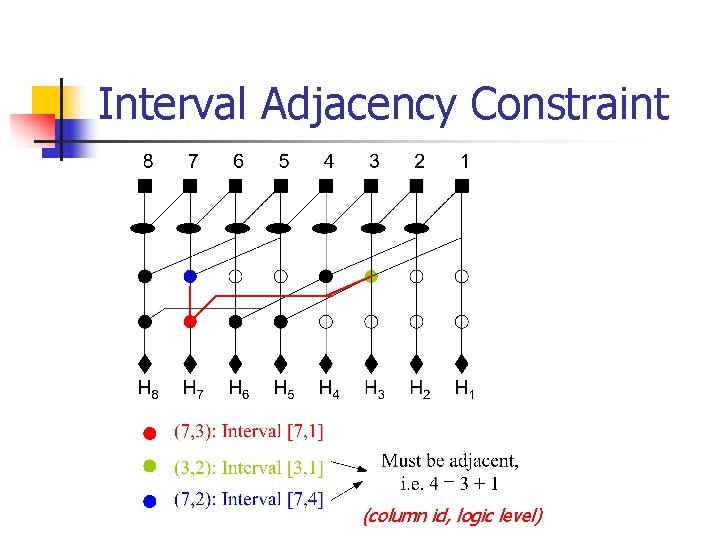
Interval Adjacency Constraint (column id, logic level)

Linearization for Interval Adjacency Constraint Left interval bound equal to column index Linearize Pseudo Linear 21

Search Space Reduction n n Ling’s adder: separate odd and even bits Double the bit-width we are able to search 22

Redundant Constraints n n Cell (i, j) is known to have logic level j before wire connection Assume load is Min. Load (fanout=1 with minimum wire length): Cell (i, j) has a path of length j-1 Assume each cell along the path has Min. Load 23

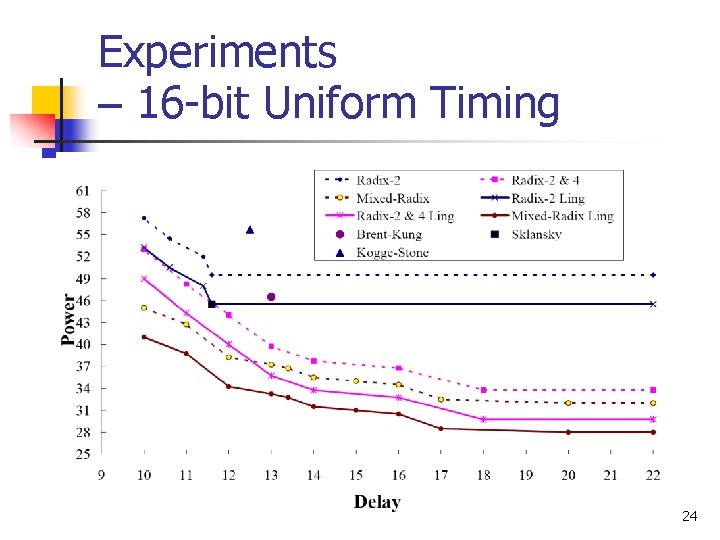
Experiments – 16 -bit Uniform Timing 24

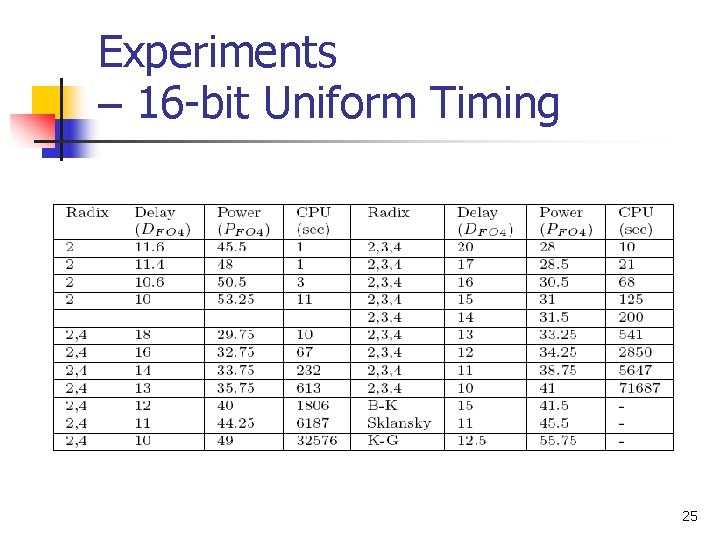
Experiments – 16 -bit Uniform Timing 25

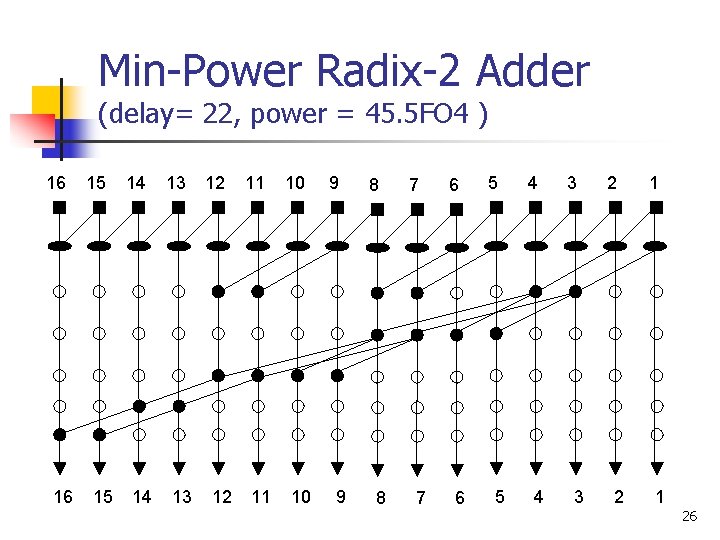
Min-Power Radix-2 Adder (delay= 22, power = 45. 5 FO 4 ) 16 16 15 15 14 14 13 13 12 12 11 11 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 26

Min-Power Radix-2&4 Adder (delay=18, power = 29. 75 FO 4 ) 16 16 15 15 14 13 14 Radix-2 Cell 13 12 12 11 11 10 10 9 9 8 8 7 7 6 6 5 5 4 4 3 3 2 2 1 1 Radix-4 Cell 27

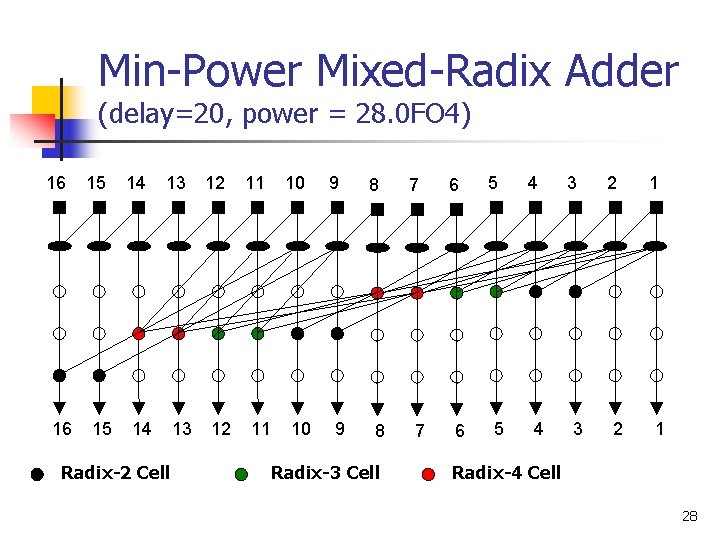
Min-Power Mixed-Radix Adder (delay=20, power = 28. 0 FO 4) 16 16 15 15 14 13 14 Radix-2 Cell 13 12 12 11 10 9 9 8 8 Radix-3 Cell 7 7 6 6 5 5 4 4 3 3 2 2 1 1 Radix-4 Cell 28

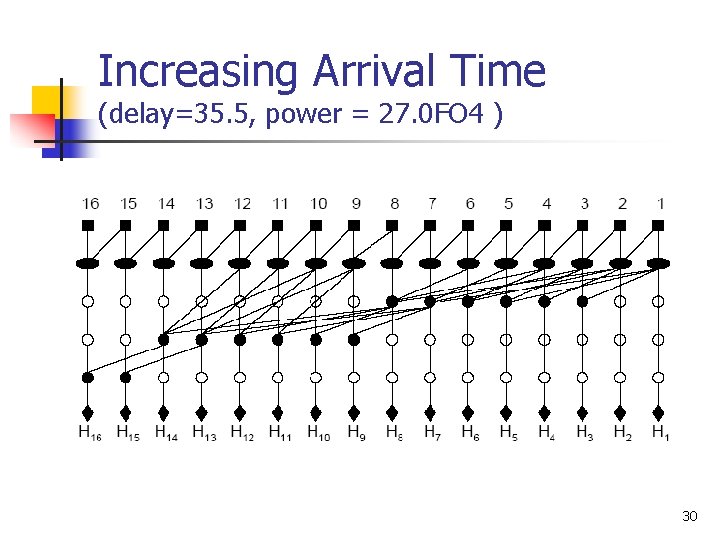
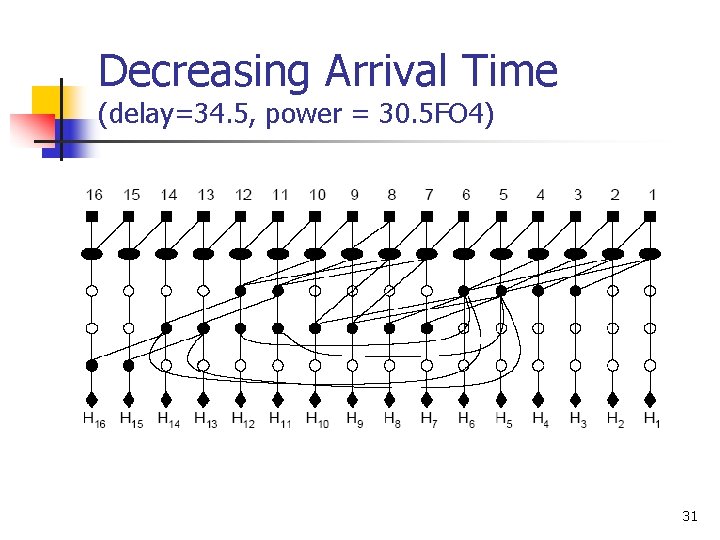
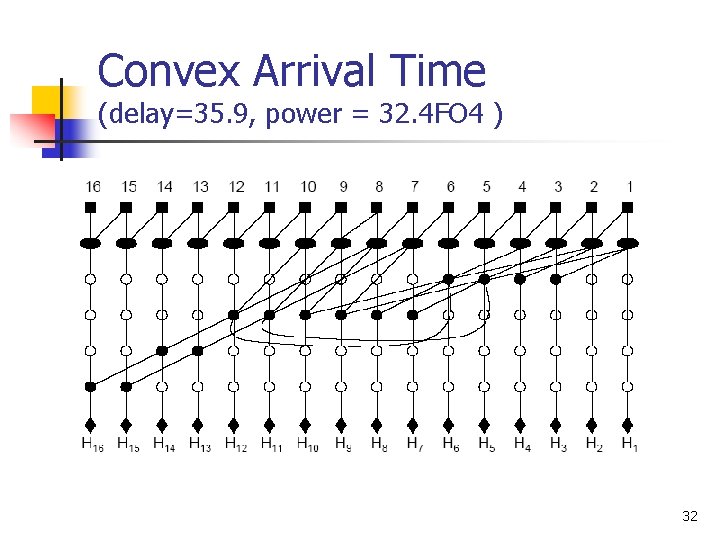
Experiments – 16 -bit Nonuniform Time (Mixed Radix) ILP is able to handle non-uniform timings Ling adders are most superior in increasing arrival time – faster carries 29

Increasing Arrival Time (delay=35. 5, power = 27. 0 FO 4 ) 30

Decreasing Arrival Time (delay=34. 5, power = 30. 5 FO 4) 31

Convex Arrival Time (delay=35. 9, power = 32. 4 FO 4 ) 32

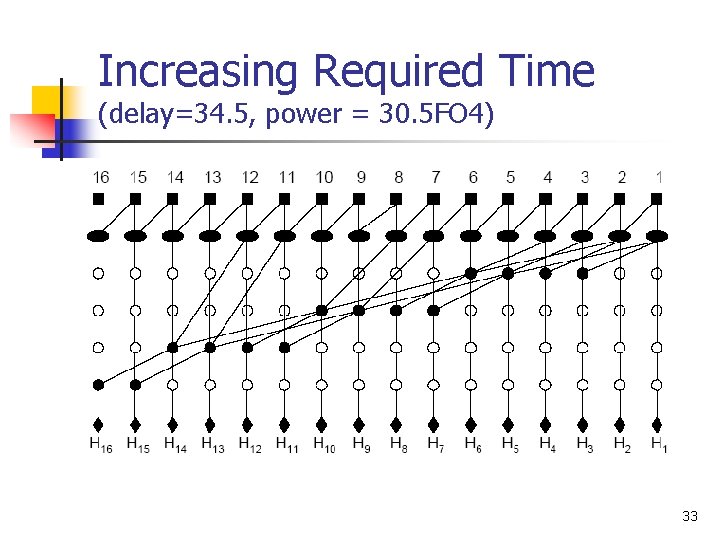
Increasing Required Time (delay=34. 5, power = 30. 5 FO 4) 33

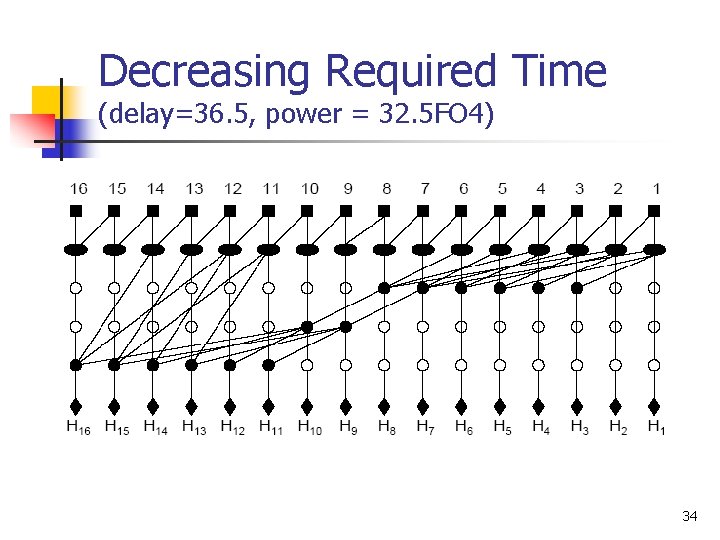
Decreasing Required Time (delay=36. 5, power = 32. 5 FO 4) 34

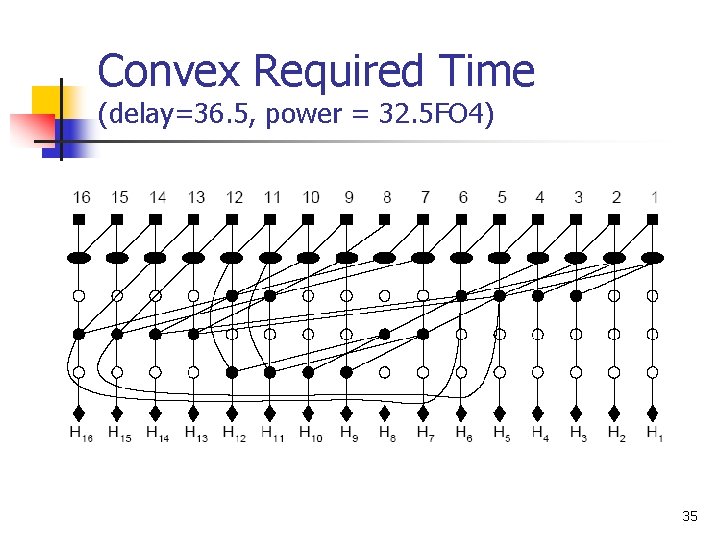
Convex Required Time (delay=36. 5, power = 32. 5 FO 4) 35

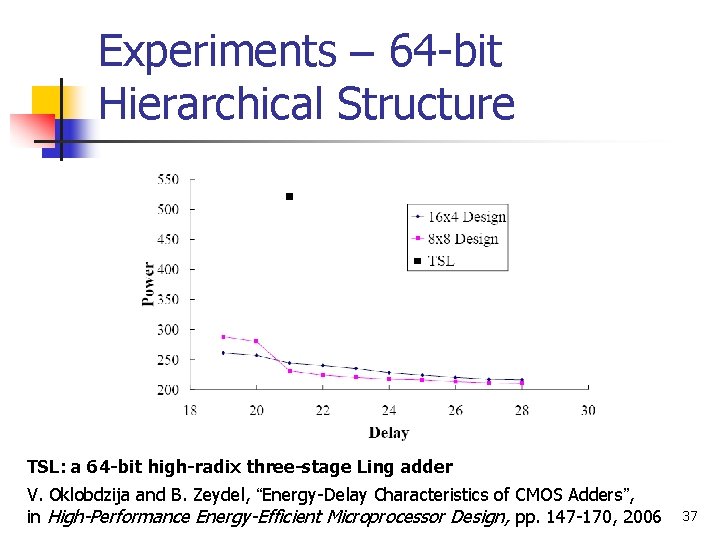
Experiments – 64 -bit Hierarchical Structure (Mixed-Radix) n n Handle high bit-width applications 16 x 4 and 8 x 8 36

Experiments – 64 -bit Hierarchical Structure TSL: a 64 -bit high-radix three-stage Ling adder V. Oklobdzija and B. Zeydel, “Energy-Delay Characteristics of CMOS Adders”, in High-Performance Energy-Efficient Microprocessor Design, pp. 147 -170, 2006 37

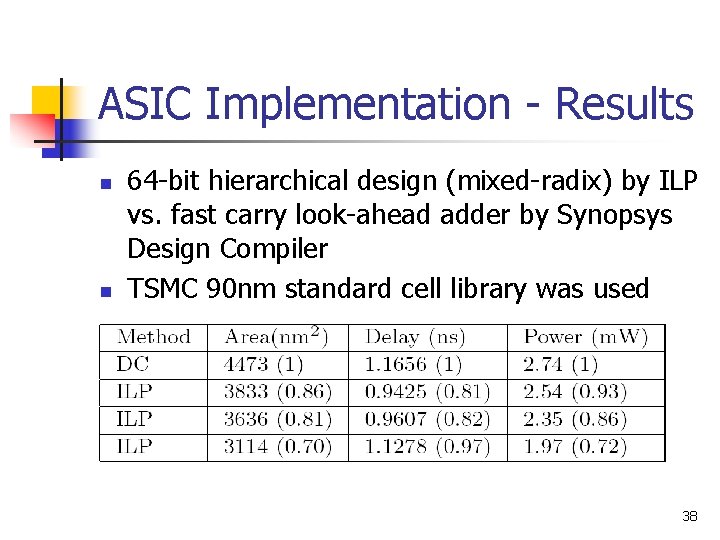
ASIC Implementation - Results n n 64 -bit hierarchical design (mixed-radix) by ILP vs. fast carry look-ahead adder by Synopsys Design Compiler TSMC 90 nm standard cell library was used 38

Future Work n ILP formulation improvement n n Expected to handle 32 or 64 bit applications without hierarchical scheme Optimizing other computer arithmetic modules n Comparator, Multiplier 39

Q&A Thank You! 40