Decision making under uncertainty Stochastic methods in Engineering

Decision making under uncertainty Stochastic methods in Engineering Risto Lahdelma Professor, Energy for communities

Content • • • What is uncertainty Stochastic dominance Utility theory Risk attitude Multi-criteria decision analysis Multicriteria utility function

What is uncertainty ”I used to be uncertain, but now I am not sure” • Uncertainty can mean different things – – Inaccurate: his height is 190 cm Imprecise: his height is in range [185, 195] Fuzzy (vague): he is tall Classical probability: tossing heads on a fair coin has 50% probability – Subjective probability: I believe there is 50% chance for rain tomorrow – Statistical probability: I win my friend in Badminton 6 times out of 10

Representing uncertainty • Many ways – Standard uncertainty, confidence margins, fuzzy sets, rough sets, … • Different kinds of uncertainty can be represented using probability distributions – In most cases this is an approximation of reality – Almost nothing is certain – not even the probability distribution to represent uncertainty – Still we must represent uncertainty the best we can and consider it in decision making

Biases in estimating uncertainty • People cannot assess probabilities well – After tossing 6 heads on a coin, what is more likely next, heads of tails? – When tossing a coin, which sequence is more likely, HHHTTT or HTHTHT ? – You see a good looking woman in a bar. Is she more likely a model or nurse? – Is it more likely that an English word starts with K or that K is the third letter? – Is the percentage of African countries in UN greater or less than xx%? How large?

Biases in estimating uncertainty – Which is more likely, getting 7 figures right on Lotto or dying in car accident while submitting Lotto coupon? – If the probability of rain is 50% on Saturday and 50% on Sunday, what is the probability that it will rain during weekend? – Which number series has greater variance: A: 6 B: 1110 18 1122 4 1108 5 1109 17 1121 – Which is more likely: A: That Williams loses the first set in Tennis. B: That Williams loses the first set but wins the match. – Estimate 90% confidence margin for the distance to the second brightest star Canopus (in light years).

Decision under uncertainty • Many different approaches to compare uncertain alternatives – Single criterion decision making • Typically, money is the criterion • Different aspects of the decision alternatives are expressed in monetary units – Multiple criterion decision making • Multiple non-commensurate criteria (objectives) must be considered simultaneously

Stochastic dominance • You have to choose between a 1, a 2, a 3 with outcomes at probabilities 1, 2, 3 • Such dominating alternative does not often exist

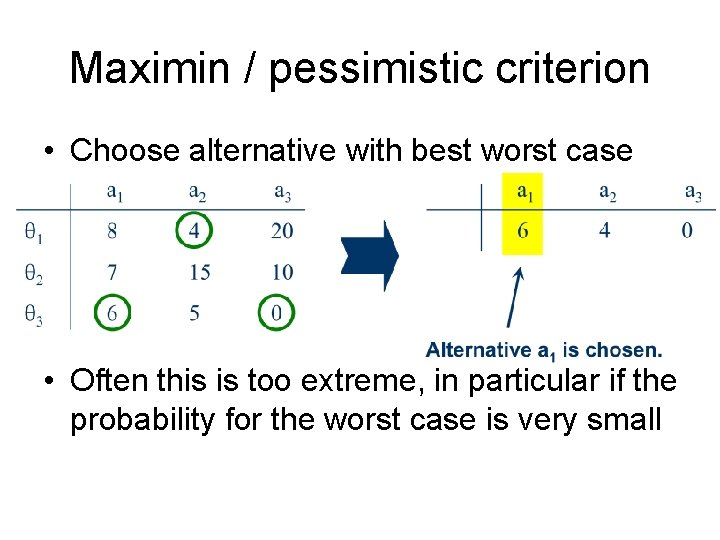
Maximin / pessimistic criterion • Choose alternative with best worst case • Often this is too extreme, in particular if the probability for the worst case is very small

Maximax / optimistic criterion • Choose alternative with best case • Also this is may be unwise

Expected value • Choose best expected value • Commonly used • People do not often behave like this

Gamble situation • Which alternative do you prefer? A) 10 000 € for sure B) 20 000 € for p=0. 6 but 0 for p=0. 4 – Expected value of B is 12 000

Gamble situation • Which alternative do you prefer? A) 10 000 € for sure B) 20 000 € for p=0. 6 but 0 for p=0. 4 – Expected value of B is 12 000 • Many people choose A • This behaviour is called risk aversion – A certain outcome is preferred to a risky choice with a little higher expected value

Utility theory • Preferences in the precence of risk can be modelled using a utility function u(x) • The u(x) is a monotonic function that maps the worst outcome to 0 and the best outcome to 1 • The decision maker (DM) maximises the expected utility E(u(x))

Expected utility • For discrete case x = <p 1, x 1 ; . . . pn, xn > E(u(x)) = i piu(xi) • For continuous case x with density f(x) E(u(x)) = x f (x)u(x)dx

Risk averse DM • Risk averse DM prefers certain outcome to gamble with (little) higher expected value – A rational DM is normally assumed to be risk averse or risk neutral – Opposite of risk averse is risk-seeking, who prefers a gamble

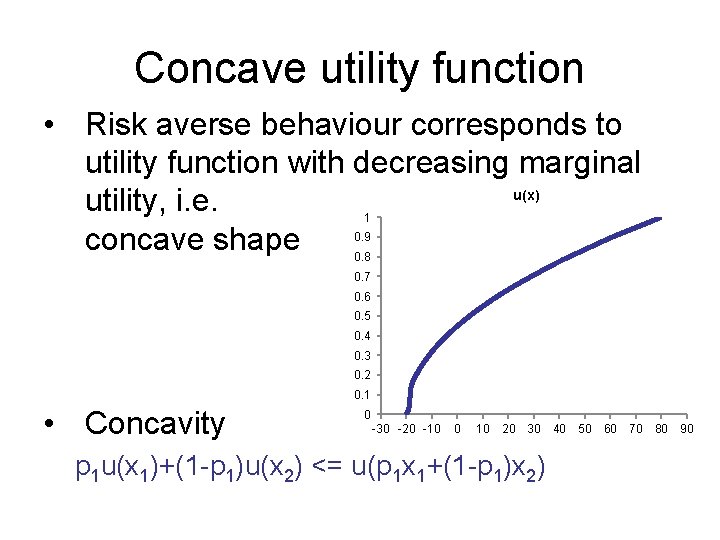
Concave utility function • Risk averse behaviour corresponds to utility function with decreasing marginal u(x) utility, i. e. concave shape 1 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 2 0. 1 • Concavity 0 -30 -20 -10 0 10 20 30 p 1 u(x 1)+(1 -p 1)u(x 2) <= u(p 1 x 1+(1 -p 1)x 2) 40 50 60 70 80 90

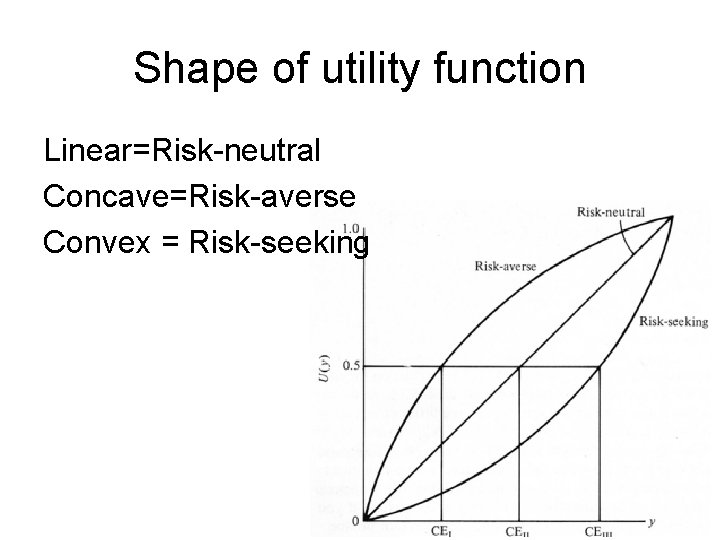
Shape of utility function Linear=Risk-neutral Concave=Risk-averse Convex = Risk-seeking

Example • To drill or not drill for oil A) Cost of drilling is 20, chance of finding is 25%, profit in this case is 80 B) Don’t drill, no cost, no profit – Utility function u(x) = (20+x)0. 5/10 u(A) = (0. 25*10+0. 75*0)/10 = 0. 25 u(B) = ( 20)/10 0. 447 • Don’t drill. – (using expected values, E(A)=5, E(B)=0)

Multicriteria decision making • Choosing most preferred alternative considering multiple non-commensurate criteria – If all criteria can be made commensurate, expressed e. g. in money, then the problem reduces into single criterion – Sometimes this is not possible or desired to do that – Some criteria are really difficult to combine

Non-commensurate criteria • Examples – – Cost, quality, reliability Economy, environment, human health Effects on different interest groups Energy efficiency, emissions, service level

Multicriteria utility function • Utility is a function with multiple arguments u(x 1, x 2, …, xn) – – Cost, quality, reliability Economy, environment, human health Effects on different interest groups Energy efficiency, emissions, service level

Multicriteria utility function – 2 -criterion example • The City is considering four sites (A, B, C and D) for a new power plant • The objectives of the city are to – minimise the cost of building the station; – minimise the area of land damaged by building it. • Factors influencing the objectives include – the land type at the different sites, – the architect and construction company hired, – cost of material and machines used, the weather, etc.

Multicriteria utility function – 2 -criterion example • Criteria evaluation – Costs, are estimated to fall between 15 M€ and 60 M€ – between 200 and 600 hectars of land will be damaged • The possible consequences of the decision alternatives are captured by two criteria. • We need to determine a two-attribute utility function: u(Cost, Area) or u(C, A)

Multicriteria utility function assessment • Let x 1, . . . , xn, n ≥ 2, be a set of criteria associated with the consequences of a decision problem. • The utility of a consequence (x 1, . . . , xn) can be determined from direct assessment: – estimate the overall utility u(x 1, . . . , xn) over the given values of all n attributes; • Decomposed assessment: – estimate n partial utilities ui(xi) for given values of the n criteria; – Define u(x 1, . . . , xn) as combination of ui(xi) for all criteria: u(x 1, …, xn) = u(u 1(x 1), …, un(xn))

Decomposed assessment • Decomposed assessment is commonly used especially when there are many criteria – The additive form is often used • u(x 1, …, xn) = u(u 1(x 1), …, un(xn)) = w 1 u 1(x 1)+…+wnun(xn) – Here w 1, …wn are importance weights given for the criteria – Weights are subjective information that should be obtained from the DMs • If the partial utility functions are linear, then the overall utility function is linear (risk neutral behaviour) – Concave partial utility functions means risk averse behaviour

Decomposed assessment • The City models the utility as additive function. • The partial utility functions u. C and u. A are assessed u. C(15) = 1; u. C(30) = 0. 5; u. C(50) = 0. 2; u. C(60) = 0 u. A(200) = 1; u. A(300) = 0. 8; u. A(400) = 0. 5; u. A(600) = 0 • Cost is considered three times as important as Area. • Utilities for various Cost, Area pairs are then computed: – – – u(50, 300) = 3 · u. C(50) + 1 · u. A(300) = 3 · 0. 2 + 1 · 0. 8 = 1. 4 u(30, 400) = 1. 5 + 0. 5 = 2. 0 u(60, 200) = 0. 0 + 1. 0 = 1. 0 u(15, 600) = 3. 0 + 0. 0 = 3. 0 u(15, 200) = 3. 0 + 1. 0 = 4. 0

Excercise • Choose (Cost, Area) values for the four alternatives A, B, C, D • For Cost, let each alternative have two possible values with different probabilities • Compute the expected utility for the alternatives