Decision Making Under Uncertainty Russell and Norvig ch

Decision Making Under Uncertainty Russell and Norvig: ch 16, 17 CMSC 671 – Fall 2005 material from Lise Getoor, Jean-Claude Latombe, and Daphne Koller

Decision Making Under Uncertainty Many environments have multiple possible outcomes Some of these outcomes may be good; others may be bad Some may be very likely; others unlikely What’s a poor agent to do? ?

Non-Deterministic vs. Probabilistic Uncertainty ? a ? b c a b c {a, b, c} {a(pa), b(pb), c(pc)} à decision that is best for worst case à decision that maximizes expected utility value Non-deterministic model Probabilistic model ~ Adversarial search

Expected Utility Random variable X with n values x 1, …, xn and distribution (p 1, …, pn) E. g. : X is the state reached after doing an action A under uncertainty Function U of X E. g. , U is the utility of a state The expected utility of A is EU[A] = Si=1, …, n p(xi|A)U(xi)

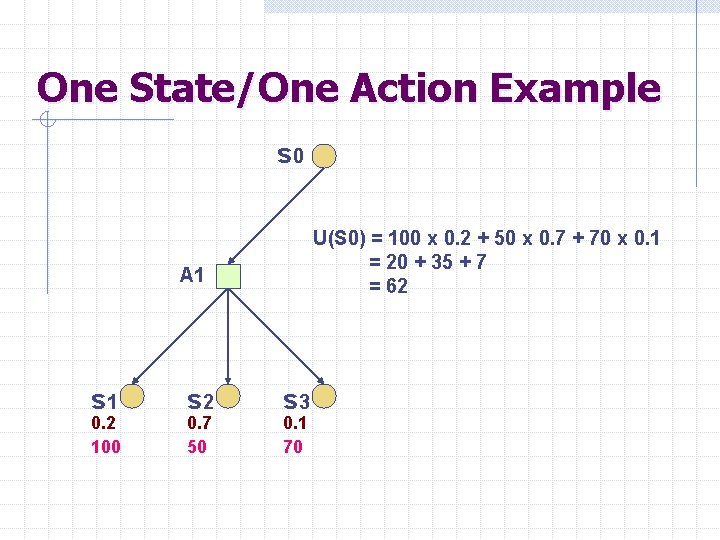
One State/One Action Example s 0 U(S 0) = 100 x 0. 2 + 50 x 0. 7 + 70 x 0. 1 = 20 + 35 + 7 = 62 A 1 s 1 0. 2 100 s 2 0. 7 50 s 3 0. 1 70

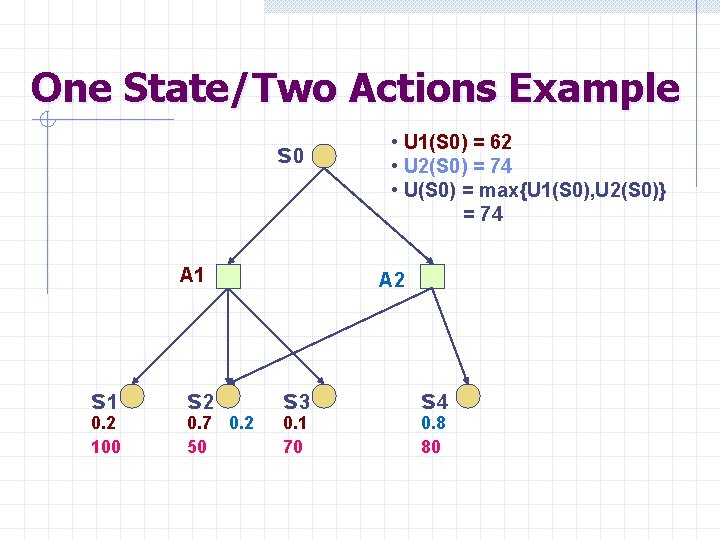
One State/Two Actions Example s 0 A 1 s 1 0. 2 100 s 2 0. 7 0. 2 50 • U 1(S 0) = 62 • U 2(S 0) = 74 • U(S 0) = max{U 1(S 0), U 2(S 0)} = 74 A 2 s 3 0. 1 70 s 4 0. 8 80

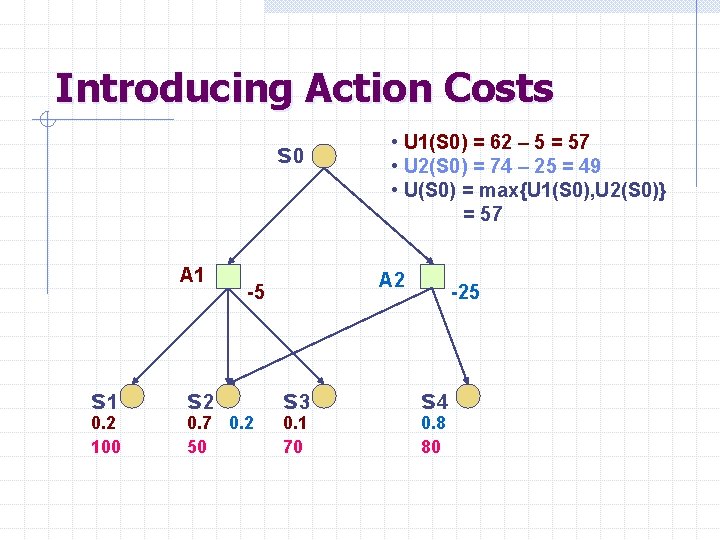
Introducing Action Costs s 0 A 1 s 1 0. 2 100 s 2 A 2 -5 0. 7 0. 2 50 • U 1(S 0) = 62 – 5 = 57 • U 2(S 0) = 74 – 25 = 49 • U(S 0) = max{U 1(S 0), U 2(S 0)} = 57 s 3 0. 1 70 -25 s 4 0. 8 80

MEU Principle A rational agent should choose the action that maximizes agent’s expected utility This is the basis of the field of decision theory The MEU principle provides a normative criterion for rational choice of action

Not quite… Must have complete model of: n n n Actions Utilities States Even if you have a complete model, will be computationally intractable In fact, a truly rational agent takes into account the utility of reasoning as well---bounded rationality Nevertheless, great progress has been made in this area recently, and we are able to solve much more complex decision-theoretic problems than ever before

We’ll look at Decision-Theoretic Planning n n Simple decision making (ch. 16) Sequential decision making (ch. 17)

Axioms of Utility Theory Orderability n (A>B) (A<B) (A~B) Transitivity n (A>B) (B>C) (A>C) Continuity n A>B>C p [p, A; 1 -p, C] ~ B Substitutability n A~B [p, A; 1 -p, C]~[p, B; 1 -p, C] Monotonicity n A>B (p≥q [p, A; 1 -p, B] >~ [q, A; 1 -q, B]) Decomposability n [p, A; 1 -p, [q, B; 1 -q, C]] ~ [p, A; (1 -p)q, B; (1 -p)(1 -q), C]

Money Versus Utility Money <> Utility n More money is better, but not always in a linear relationship to the amount of money Expected Monetary Value Risk-averse – U(L) < U(SEMV(L)) Risk-seeking – U(L) > U(SEMV(L)) Risk-neutral – U(L) = U(SEMV(L))

Value Function Provides a ranking of alternatives, but not a meaningful metric scale Also known as an “ordinal utility function” Remember the expectiminimax example: n n Sometimes, only relative judgments (value functions) are necessary At other times, absolute judgments (utility functions) are required

Multiattribute Utility Theory A given state may have multiple utilities n n . . . because of multiple evaluation criteria. . . because of multiple agents (interested parties) with different utility functions We will talk about this more later in the semester, when we discuss multi-agent systems and game theory

Decision Networks Extend BNs to handle actions and utilities Also called influence diagrams Use BN inference methods to solve Perform Value of Information calculations

Decision Networks cont. Chance nodes: random variables, as in BNs Decision nodes: actions that decision maker can take Utility/value nodes: the utility of the outcome state.

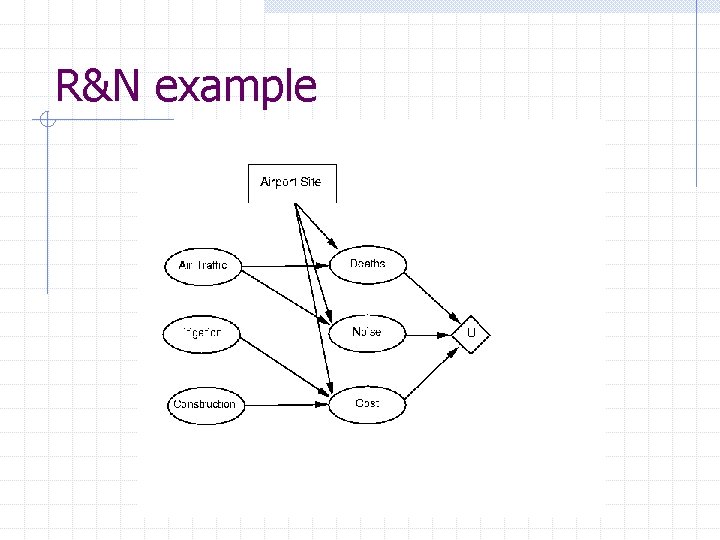
R&N example

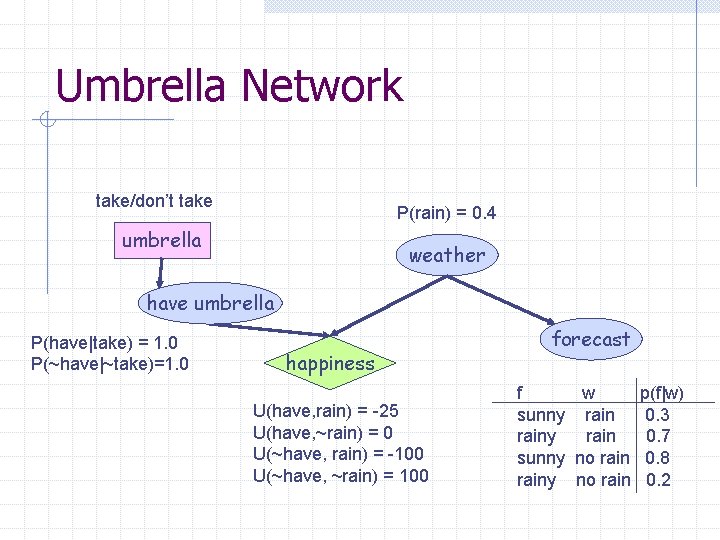
Umbrella Network take/don’t take P(rain) = 0. 4 umbrella weather have umbrella P(have|take) = 1. 0 P(~have|~take)=1. 0 happiness U(have, rain) = -25 U(have, ~rain) = 0 U(~have, rain) = -100 U(~have, ~rain) = 100 forecast f w p(f|w) sunny rain 0. 3 rainy rain 0. 7 sunny no rain 0. 8 rainy no rain 0. 2

Evaluating Decision Networks Set the evidence variables for current state For each possible value of the decision node: n n n Set decision node to that value Calculate the posterior probability of the parent nodes of the utility node, using BN inference Calculate the resulting utility for action Return the action with the highest utility

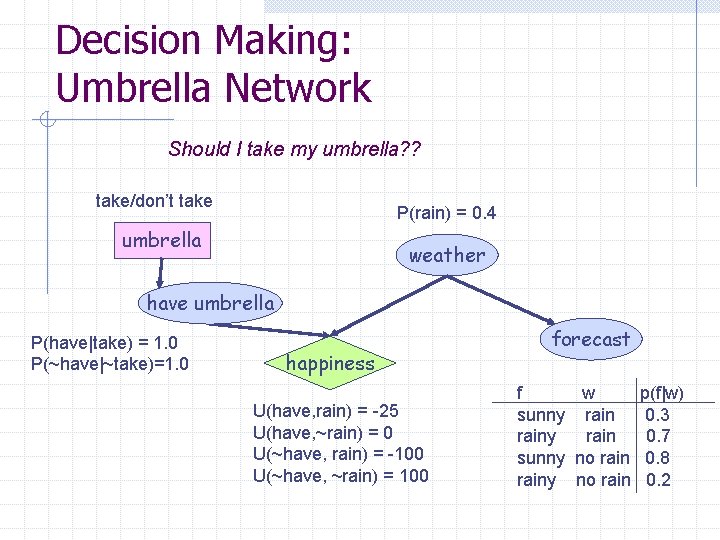
Decision Making: Umbrella Network Should I take my umbrella? ? take/don’t take P(rain) = 0. 4 umbrella weather have umbrella P(have|take) = 1. 0 P(~have|~take)=1. 0 happiness U(have, rain) = -25 U(have, ~rain) = 0 U(~have, rain) = -100 U(~have, ~rain) = 100 forecast f w p(f|w) sunny rain 0. 3 rainy rain 0. 7 sunny no rain 0. 8 rainy no rain 0. 2

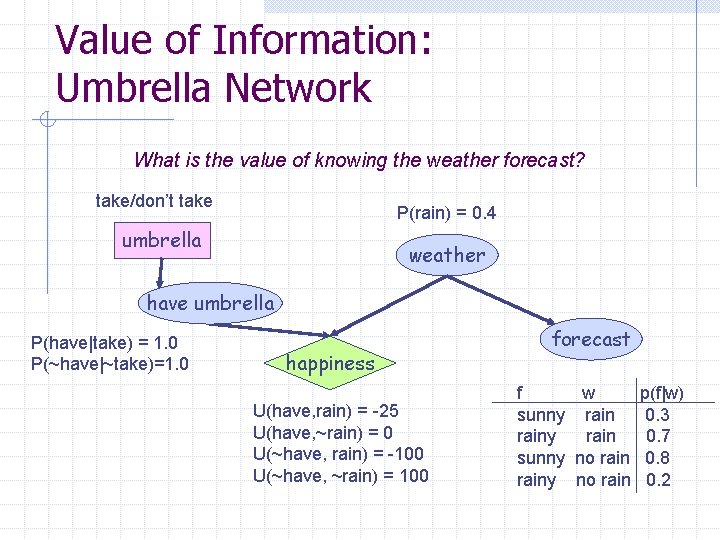
Value of Information (VOI) Suppose an agent’s current knowledge is E. The value of the current best action is The value of the new best action (after new evidence E’ is obtained): The value of information for E’ is therefore:

Value of Information: Umbrella Network What is the value of knowing the weather forecast? take/don’t take P(rain) = 0. 4 umbrella weather have umbrella P(have|take) = 1. 0 P(~have|~take)=1. 0 happiness U(have, rain) = -25 U(have, ~rain) = 0 U(~have, rain) = -100 U(~have, ~rain) = 100 forecast f w p(f|w) sunny rain 0. 3 rainy rain 0. 7 sunny no rain 0. 8 rainy no rain 0. 2

Sequential Decision Making Finite Horizon Infinite Horizon

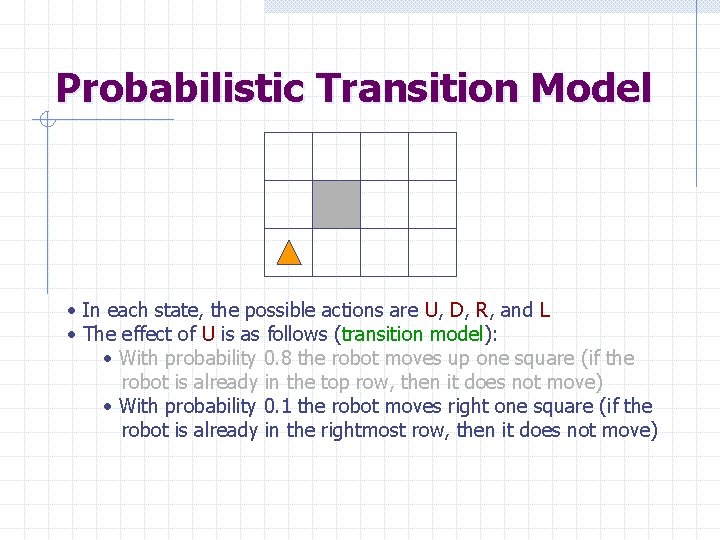
Simple Robot Navigation Problem • In each state, the possible actions are U, D, R, and L

Probabilistic Transition Model • In each state, the possible actions are U, D, R, and L • The effect of U is as follows (transition model): • With probability 0. 8 the robot moves up one square (if the robot is already in the top row, then it does not move)

Probabilistic Transition Model • In each state, the possible actions are U, D, R, and L • The effect of U is as follows (transition model): • With probability 0. 8 the robot moves up one square (if the robot is already in the top row, then it does not move) • With probability 0. 1 the robot moves right one square (if the robot is already in the rightmost row, then it does not move)

Probabilistic Transition Model • In each state, the possible actions are U, D, R, and L • The effect of U is as follows (transition model): • With probability 0. 8 the robot moves up one square (if the robot is already in the top row, then it does not move) • With probability 0. 1 the robot moves right one square (if the robot is already in the rightmost row, then it does not move) • With probability 0. 1 the robot moves left one square (if the robot is already in the leftmost row, then it does not move)

Markov Property The transition properties depend only on the current state, not on previous history (how that state was reached)

Sequence of Actions [3, 2] 3 2 1 1 2 3 4 • Planned sequence of actions: (U, R)

Sequence of Actions [3, 2] 3 [3, 2] [3, 3] [4, 2] 2 1 1 2 3 4 • Planned sequence of actions: (U, R) • U is executed

Histories [3, 2] 3 [3, 2] [3, 3] [4, 2] 2 1 1 [3, 1] [3, 2] [3, 3] [4, 1] [4, 2] [4, 3] 2 3 4 • Planned sequence of actions: (U, R) • U has been executed • R is executed • There are 9 possible sequences of states – called histories – and 6 possible final states for the robot!

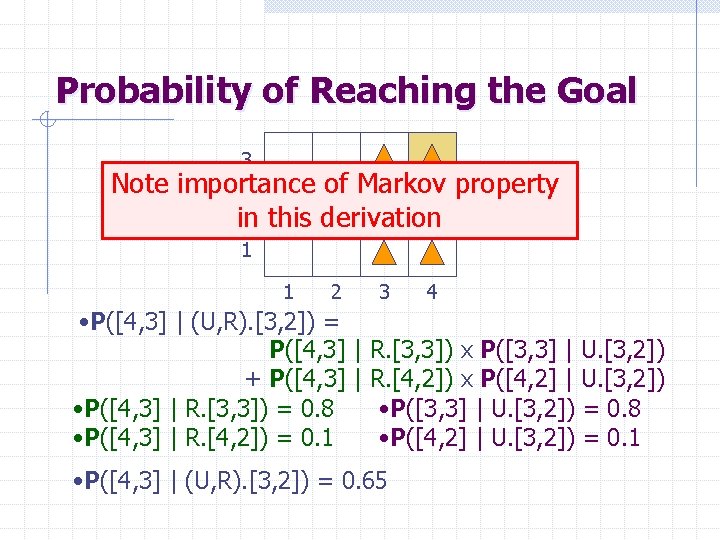
Probability of Reaching the Goal 3 Note importance of Markov property 2 in this derivation 1 1 2 3 4 • P([4, 3] | (U, R). [3, 2]) = P([4, 3] | R. [3, 3]) x P([3, 3] | U. [3, 2]) + P([4, 3] | R. [4, 2]) x P([4, 2] | U. [3, 2]) • P([4, 3] | R. [3, 3]) = 0. 8 • P([3, 3] | U. [3, 2]) = 0. 8 • P([4, 3] | R. [4, 2]) = 0. 1 • P([4, 2] | U. [3, 2]) = 0. 1 • P([4, 3] | (U, R). [3, 2]) = 0. 65

Utility Function 3 +1 2 -1 1 1 2 3 4 • [4, 3] provides power supply • [4, 2] is a sand area from which the robot cannot escape

Utility Function 3 +1 2 -1 1 1 2 3 4 • [4, 3] provides power supply • [4, 2] is a sand area from which the robot cannot escape • The robot needs to recharge its batteries

Utility Function 3 +1 2 -1 1 1 • • 2 3 4 [4, 3] provides power supply [4, 2] is a sand area from which the robot cannot escape The robot needs to recharge its batteries [4, 3] or [4, 2] are terminal states

Utility of a History 3 +1 2 -1 1 1 • • • 2 3 4 [4, 3] provides power supply [4, 2] is a sand area from which the robot cannot escape The robot needs to recharge its batteries [4, 3] or [4, 2] are terminal states The utility of a history is defined by the utility of the last state (+1 or – 1) minus n/25, where n is the number of moves

Utility of an Action Sequence 3 +1 2 -1 1 1 2 3 4 • Consider the action sequence (U, R) from [3, 2]

Utility of an Action Sequence 3 +1 [3, 2] 2 -1 [3, 2] [3, 3] [4, 2] 1 1 2 3 4 [3, 1] [3, 2] [3, 3] [4, 1] [4, 2] [4, 3] • Consider the action sequence (U, R) from [3, 2] • A run produces one among 7 possible histories, each with some probability

Utility of an Action Sequence 3 +1 [3, 2] 2 -1 [3, 2] [3, 3] [4, 2] 1 1 2 3 4 [3, 1] [3, 2] [3, 3] [4, 1] [4, 2] [4, 3] • Consider the action sequence (U, R) from [3, 2] • A run produces one among 7 possible histories, each with some probability • The utility of the sequence is the expected utility of the histories: U = Sh. Uh P(h)

Optimal Action Sequence 3 +1 [3, 2] 2 -1 [3, 2] [3, 3] [4, 2] 1 1 2 3 4 [3, 1] [3, 2] [3, 3] [4, 1] [4, 2] [4, 3] • Consider the action sequence (U, R) from [3, 2] • A run produces one among 7 possible histories, each with some probability • The utility of the sequence is the expected utility of the histories • The optimal sequence is the one with maximal utility

Optimal Action Sequence 3 +1 [3, 2] 2 -1 [3, 2] [3, 3] [4, 2] 1 1 2 3 4 [3, 1] [3, 2] [3, 3] [4, 1] [4, 2] [4, 3] • Consider the action sequence (U, R) from [3, 2] • A run produces among 7 possible each with some onlyone if the sequence is histories, executed blindly! probability • The utility of the sequence is the expected utility of the histories • The optimal sequence is the one with maximal utility • But is the optimal action sequence what we want to compute?

Reactive Agent Algorithm Accessible or Repeat: observable state w s sensed state w If s is terminal then exit w a choose action (given s) w Perform a

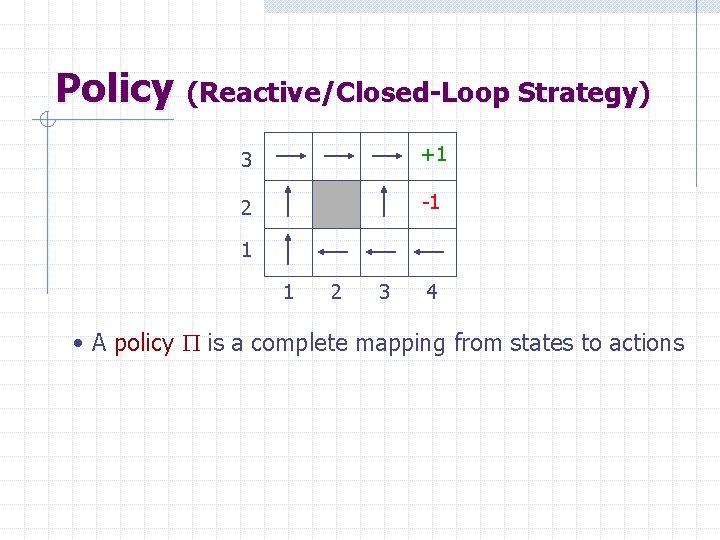
Policy (Reactive/Closed-Loop Strategy) 3 +1 2 -1 1 1 2 3 4 • A policy P is a complete mapping from states to actions

Reactive Agent Algorithm Repeat: w s sensed state w If s is terminal then exit w a P(s) w Perform a

Optimal Policy 3 +1 2 -1 1 1 2 3 4 that [3, 2] a “dangerous” • A policy P is a complete. Note mapping from is states to actions state optimal policy • The optimal policy P* is the onethatthe always yields a tries to maximal avoid history (ending at a terminal state) with expected utility Makes sense because of Markov property

Optimal Policy 3 +1 2 -1 1 1 2 3 4 This problem calledtoa actions • A policy P is a complete mapping from isstates Decision Problemyields (MDP) • The optimal policy P*Markov is the one that always a history with maximal expected utility How to compute P*?

Additive Utility History H = (s 0, s 1, …, sn) The utility of H is additive iff: U(s , …, s ) = R(0) + U(s , …, s ) = S R(i) 0 1 n Reward

Additive Utility History H = (s 0, s 1, …, sn) The utility of H is additive iff: U(s , …, s ) = R(0) + U(s , …, s ) 0 1 n 1 Robot navigation example: n R(n) = +1 if sn = [4, 3] n R(n) = -1 if sn = [4, 2] n R(i) = -1/25 if i = 0, …, n-1 n = S R(i)

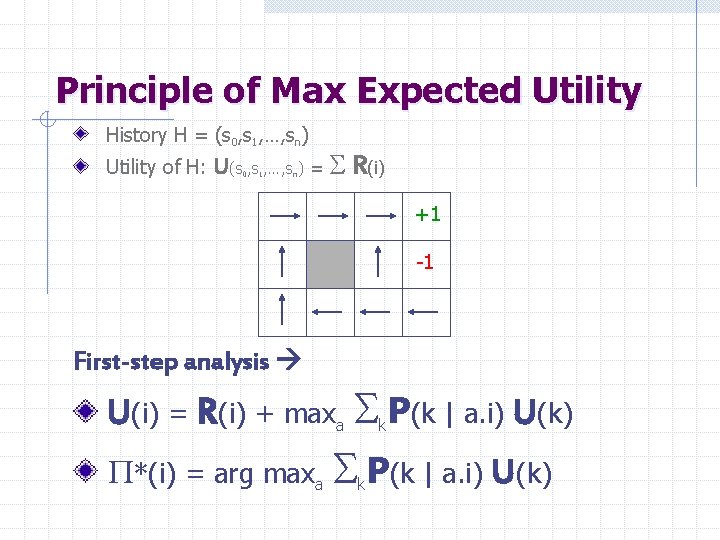
Principle of Max Expected Utility History H = (s 0, s 1, …, sn) Utility of H: U(s , …, s ) = S R(i) 0 1 n +1 -1 First-step analysis U(i) = R(i) + maxa Sk. P(k | a. i) U(k) P*(i) = arg maxa Sk. P(k | a. i) U(k)

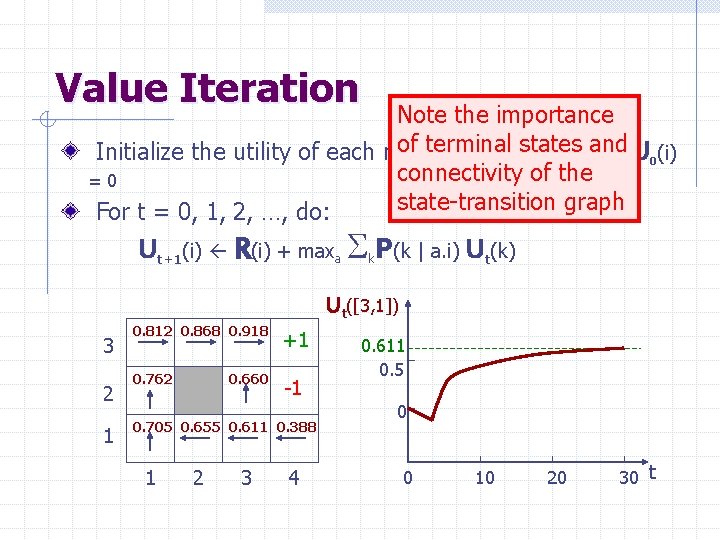
Value Iteration Initialize the utility of each non-terminal state si to U 0(i) =0 For t = 0, 1, 2, …, do: Ut+1(i) R(i) + maxa Sk. P(k | a. i) Ut(k) 3 +1 2 -1 1 1 2 3 4

Value Iteration Note the importance of terminal states Initialize the utility of each non-terminal state sand i to U 0(i) connectivity of the =0 state-transition graph For t = 0, 1, 2, …, do: Ut+1(i) R(i) + maxa Sk. P(k | a. i) Ut(k) Ut([3, 1]) 3 2 1 0. 812 0. 868 0. 918 +1 0. 762 -1 0. 660 0. 705 0. 655 0. 611 0. 388 1 2 3 4 0. 611 0. 5 0 0 10 20 30 t

Policy Iteration Pick a policy P at random

Policy Iteration Pick a policy P at random Repeat: n Compute the utility of each state for P Ut+1(i) R(i) + Sk. P(k | P(i). i) Ut(k)

Policy Iteration Pick a policy P at random Repeat: n n Compute the utility of each state for P Ut+1(i) R(i) + Sk. P(k | P(i). i) Ut(k) Compute the policy P’ given these utilities P’(i) = arg maxa S P(k | a. i) U(k) k

Policy Iteration Pick a policy P at random Repeat: n n Compute the utility of each state for P Ut+1(i) R(i) + Sk. P(k | P(i). i) Ut(k) Compute the policy P’ given these utilities P’(i) = arg maxa n Or solve the set of linear equations: S P(k | a. i) U(k) k U(i) = R(i) + Sk. P(k | P(i). i) U(k) If P’ = P then return Pa sparse system) (often

Infinite Horizon In many problems, e. g. , the robot navigation example, histories are What if the robot lives forever? potentially unbounded and the same Onemany trick: state can be reached times 3 +1 2 -1 1 1 2 3 4 Use discounting to make infinite Horizon problem mathematically tractable

Example: Tracking a Target An optimal policy cannot be computed ahead of time: - The environment might be unknown - The environment may only be partially observable - The target may not wait A policy must be computed “on-the-fly” • The robot must keep the target in view • The target’s trajectory is not known in advance • The environment may target robot or may not be known

POMDP (Partially Observable Markov Decision Problem) • A sensing operation returns multiple states, with a probability distribution • Choosing the action that maximizes the expected utility of this state distribution assuming “state utilities” computed as above is not good enough, and actually does not make sense (is not rational)

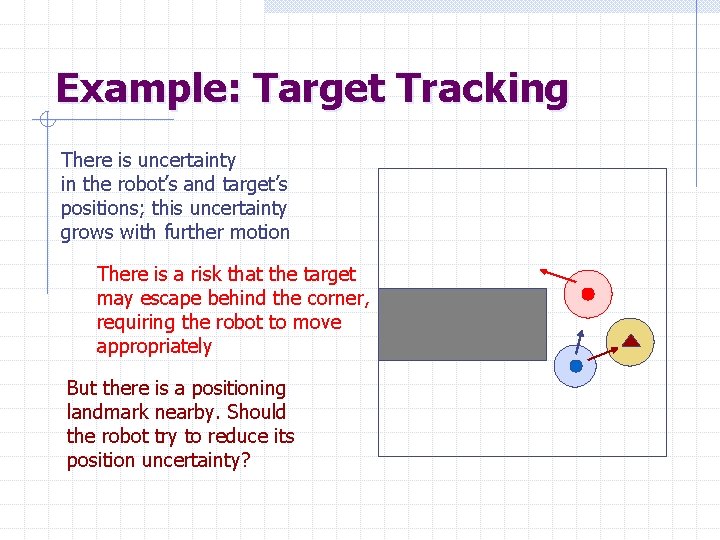
Example: Target Tracking There is uncertainty in the robot’s and target’s positions; this uncertainty grows with further motion There is a risk that the target may escape behind the corner, requiring the robot to move appropriately But there is a positioning landmark nearby. Should the robot try to reduce its position uncertainty?

Summary Decision making under uncertainty Utility function Optimal policy Maximal expected utility Value iteration Policy iteration