CSE 105 THEORY OF COMPUTATION Fall 2017 http

CSE 105 THEORY OF COMPUTATION Fall 2017 http: //cseweb. ucsd. edu/classes/fa 17/cse 105 -a/

Today's learning goals Sipser Ch 1. 4, 2. 1 • Apply the Pumping Lemma in proofs of nonregularity • Identify some nonregular sets • Define context-free grammars • Test if a specific string can be generated by a given context-free grammar

Pumping Lemma Sipser p. 78 Theorem 1. 70 # states in DFA recognizing A Transition labels along loop

Proof strategy To prove that a language L is not regular • Assume towards a contradiction that it is. • Use Pumping Lemma to give p, a pumping length for L • Show that p actually isn't a pumping length for L. • • Conclude that L is not regular.

Another example Claim: The set {anbman | m, n≥ 0} is not regular. Proof: …Consider the string s = …… You must pick s carefully: we want |s|≥p and s in L. Now we will demonstrate that "s cannot be pumped", thereby contradicting the assumption that p is a pumping length. Which choices of s cannot be used to complete the proof? A. s = apbp B. s = abpa C. s = apbpap D. s = apbap E. None of the above (all of these choices work).

Another example Claim: The set {anbman | m, n≥ 0} is not regular. Proof: …Consider the string s = …… You must pick s carefully: we want |s|≥p and s in L. Now we will prove a contradiction with the statement "s can be pumped" Consider an arbitrary choice of x, y, z such that s = xyz, |y|>0, |xy|≤p. This means that. . . What properties are guaranteed about x, y, z? Consider i=… In this case, xyiz = …, which is not in L, a contradiction with the Pumping Lemma applying to L and so L is not regular.

Regular sets: not the end of the story • Many nice / simple / important sets are not regular • Limitation of the finite-state automaton model • Can't "count" • Can only remember finitely far into the past • Can't backtrack • Must make decisions in "real-time" • We know computers are more powerful than this model… Which conditions should we relax?

The next model of computation • Idea: allow some memory of unbounded size • How? • Generalization of regular expressions Context-free grammars • Generalization for DFA Pushdown Automata

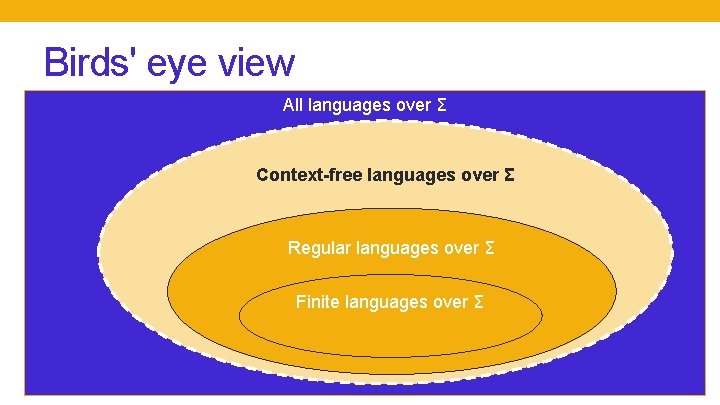
Birds' eye view All languages over Σ Context-free languages over Σ Regular languages over Σ Finite languages over Σ

Context-free grammar Sipser Def 2. 2, page 102 (V, Σ, R, S) Variables: finite set of (usually upper case) variables V Terminals: finite set of alphabet symbols Σ Rules/Productions: finite set of allowed transformations R Start variable: origination of each derivation S

Context-free language Sipser p. 104 The language generated by a CFG (V, Σ, R, S) is { w in Σ* | Starting with the Start variable and applying one or more rules, can derive w on RHS} If G = (V, Σ, R, S) the language generated by G is denoted L(G). Notation: Terminology: sequence of rule applications is derivation

An example? Consider the CFG ({S}, {0}, R, S) where R is the following set of rules S 0 S S 0 Is this a well-formed definition? A. No: there's more than one rule B. No: the same LHS gets sent to two different strings. C. No: one of the string in the RHS has both variables and literals D. Yes. E. I don't know.

Context-free language Sipser p. 104 For CFG G = (V, Σ, R, S), L(G) = { w in Σ* | Starting with the Start variable and applying one or more rules, can derive w on RHS}. What is the language of the CFG ({S}, {0}, R, S) with R = {S 0 S, S 0} ? A. {0} B. {0, 0 S} D. {ε, 0, 000, …} C. {0, 000, …} E. I don't know.

Context-free language Sipser p. 104 What is the language of the CFG ({S}, {0, 1}, R, S) with R = the set of rules S 0 S | 1 S | ε S 1 S S ε A. L(0*1*) D. L ( (0*1*) )* B. L(0* U 1*) C. L( (0 U 1) *) E. I don't know.

Designing a CFG Building a CFG to describe the language { abba } V = { S, T, V, W } Σ = { a, b } R = { S a. T S T b. V V b. W Can CFGs describe simple sets? W a }

Designing a CFG Building a CFG to describe the language { abba } V= Σ= R= S= Can CFGs describe simple sets? What's the set of terminals of this CFG? A. {a, b} B. V U S U Σ C. {S, a, b} D. {a, b, ε} E. I don't know.

Designing a CFG Building a CFG to describe the language { abba } Can CFGs describe simple sets? ( { S, T, V, W } , { a, b } , { S a. T , T b. V , V b. W , W a }, S ) OR ( { S } , { a, b } , { S abba } , S )

Is every regular language a CFL? • Approach 1: start with an arbitrary DFA M, build a CFG that generates L(M). • Approach 2: build CFGs for {a}, {ε}, {}; then show that the class of CFL is closed under the regular operations (union, concatenation, Kleene star).

Approach 1 Claim: Given any DFA M, there is a CFG whose language is L(M). Construction: Trace computation using variables to denote state Given M = (Q, Σ, δ, q 0, F) a DFA, define the CFG V = { Si | qi is in Q } Σ R = { Si a. Sj | δ(qi, a) = qj } U { Si ε | qi is in F} S = S 0 prove correctness… Then

Approach 2 If G 1 = (V 1, Σ, R 1, S 1) and G 2 = (V 2, Σ, R 2, S 2) are CFGs and G 1 describes L 1, G 2 describes L 2, how can we combine the grammars so we describe L 1 U L 2 ? A. G = (V 1 U V 2, Σ, R 1 U R 2, S 1 U S 2) B. G = (V 1 x V 2, Σ, R 1 x R 2, (S 1, S 2) ) C. We might not always be able to: the class of CFG describable languages might not be closed under union. D. I don't know.

Approach 2 If G 1 = (V 1, Σ, R 1, S 1) and G 2 = (V 2, Σ, R 2, S 2) are CFGs and G 1 describes L 1, G 2 describes L 2, how can we combine the grammars so we describe L 1 U L 2 ?

Designing a CFG Building a CFG to describe the language { a nb n | n ≥ 0 } We know this set is not regular!

Designing a CFG Building a CFG to describe the language { a nb n | n ≥ 0 } One approach: - what is shortest string in the language? - how do we go from shorter strings to longer ones?

Designing a CFG Building a CFG to describe the language { a nb n | n ≥ 0 } V={S} Σ = { a, b } R= S Which rules would complete this CFG? A. B. C. D. E. S ε | ab S ε | a. S | Sb S ε | a. Sb We need another variable other than S. I don't know.

Designing a CFG Building a CFG to describe the language { 0 n 1 m 2 n | n, m ≥ 0 } Hint: work from the outside in. Also not a regular set

Designing a CFG Also not a regular set Building a CFG to describe the language { 0 n 1 m 2 n | n, m ≥ 0 } Hint: work from the outside in. V = { S, T } Σ = { 0, 1, 2 } R = { S 0 S 2 | T | ε , S T 1 T | ε }