CSC 401 Analysis of Algorithms Chapter 6 Graphs

CSC 401 – Analysis of Algorithms Chapter 6 Graphs Objectives: • Introduce graphs and data structures • Discuss the graph connectivity and biconnectivity • Present the depth-first and breath-first search algorithms as well as algorithms for finding biconnected components • Introduce directed graphs and algorithms performed on directed graphs: Reachability, transitive closure, DAG CSC 401: Analysis of Algorithms 6 -1

Graph A graph is a pair (V, E), where – – – V is a set of nodes, called vertices E is a collection of pairs of vertices, called edges Vertices and edges are positions and store elements Example: 337 HNL 2555 LAX 3 4 7 1 1233 802 – A vertex represents an airport and stores the three-letter airport code – An edge represents a flight route between two airports and stores the mileage of the route 849 PVD 3 ORD 184 2 14 SFO 7 138 DFW CSC 401: Analysis of Algorithms LGA 1120 10 99 MIA 2

Edge Types Directed edge – – – ordered pair of vertices (u, v) first vertex u is the origin second vertex v is the destination – e. g. , a flight ORD flight AA 1206 PVD Undirected edge – unordered pair of vertices (u, v) – e. g. , a flight route Directed graph – all the edges are directed – e. g. , route network ORD 849 miles PVD Undirected graph – all the edges are undirected – e. g. , flight network CSC 401: Analysis of Algorithms 3

Terminology End vertices (or endpoints) of an edge – U and V are the endpoints of a Edges incident on a vertex – a, d, and b are incident on V Adjacent vertices – U and V are adjacent Degree of a vertex – X has degree 5 a V U b d X c e W Parallel edges h – h and i are parallel edges Self-loop – j is a self-loop CSC 401: Analysis of Algorithms j Z i g f Y 4

Terminology (cont. ) Path – sequence of alternating vertices and edges – begins with a vertex – ends with a vertex – each edge is preceded and followed by its endpoints Simple path – path such that all its vertices and edges are distinct a U c Examples – P 1=(V, b, X, h, Z) is a simple path – P 2=(U, c, W, e, X, g, Y, f, W, d, V) is a path that is not simple CSC 401: Analysis of Algorithms V b d P 2 P 1 X e W h Z g f Y 5

Terminology (cont. ) Cycle – circular sequence of alternating vertices and edges a – each edge is preceded and followed by its endpoints Simple cycle U – cycle such that all its vertices c and edges are distinct Examples – C 1=(V, b, X, g, Y, f, W, c, U, a, ) is a simple cycle – C 2=(U, c, W, e, X, g, Y, f, W, d, V, a, ) is a cycle that is not simple CSC 401: Analysis of Algorithms V b d C 2 X e C 1 g W f h Z Y 6

Property 1 Properties Notation Sv deg(v) = 2 m n Proof: each edge is counted twice Property 2 In an undirected graph with no self-loops and no multiple edges m n (n - 1)/2 Proof: each vertex has degree at most (n - 1) m deg(v) What is the bound for a directed graph? CSC 401: Analysis of Algorithms number of vertices number of edges degree of vertex v Example – n=4 – m=6 – deg(v) = 3 7

Main Methods of the Graph ADT Vertices and edges – are positions – store elements Accessor methods – – – – a. Vertex() incident. Edges(v) end. Vertices(e) is. Directed(e) origin(e) destination(e) opposite(v, e) are. Adjacent(v, w) Update methods – – – insert. Vertex(o) insert. Edge(v, w, o) insert. Directed. Edge(v, w, o) remove. Vertex(v) remove. Edge(e) Generic methods – – num. Vertices() num. Edges() vertices() edges() CSC 401: Analysis of Algorithms 8

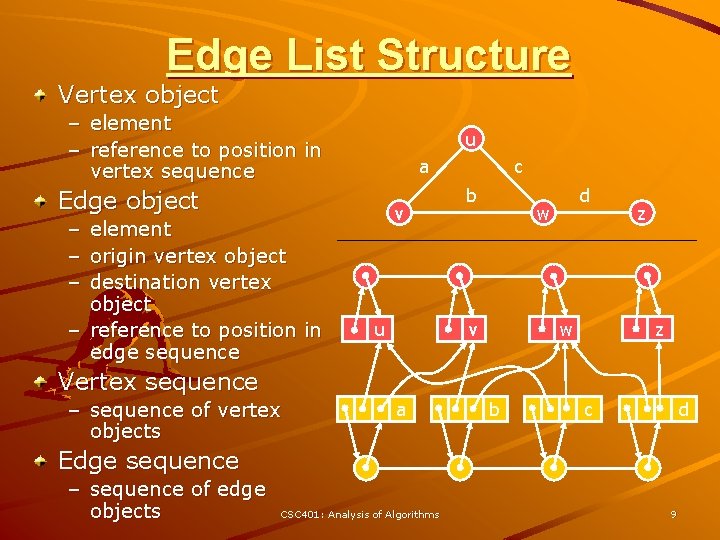
Edge List Structure Vertex object – element – reference to position in vertex sequence u a Edge object – element – origin vertex object – destination vertex object – reference to position in edge sequence v u c b d w z w v z Vertex sequence – sequence of vertex objects a b c d Edge sequence – sequence of edge objects CSC 401: Analysis of Algorithms 9

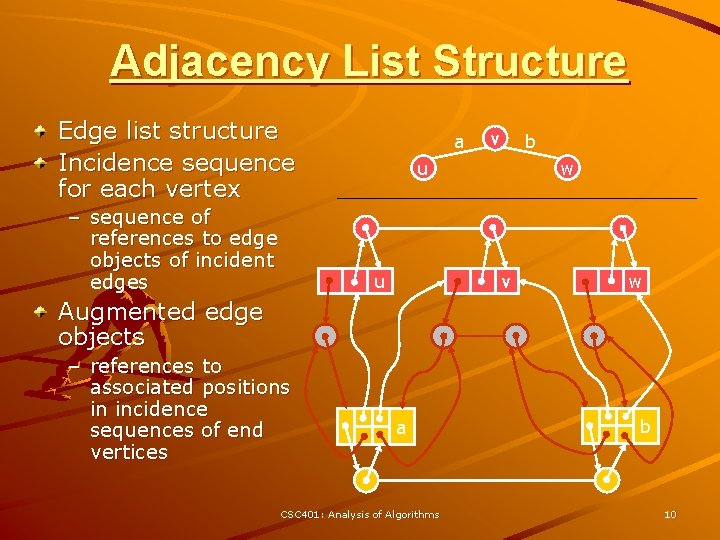
Adjacency List Structure Edge list structure Incidence sequence for each vertex – sequence of references to edge objects of incident edges a v b u u w v w Augmented edge objects – references to associated positions in incidence sequences of end vertices a CSC 401: Analysis of Algorithms b 10

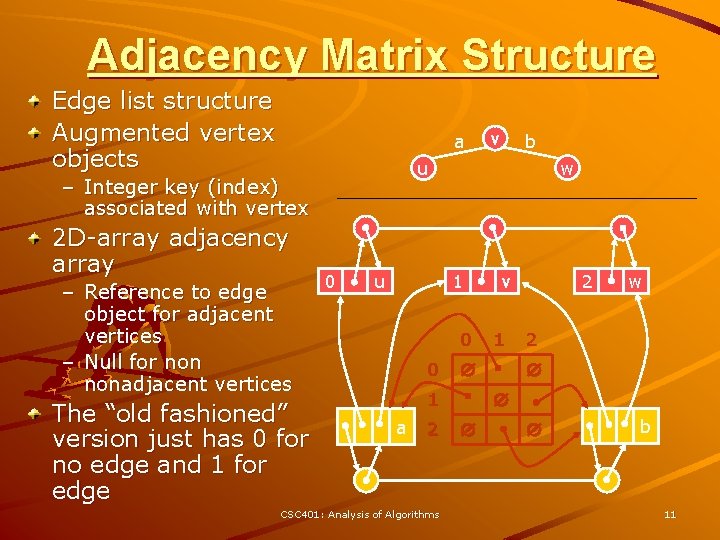
Adjacency Matrix Structure Edge list structure Augmented vertex objects a – Reference to edge object for adjacent vertices – Null for nonadjacent vertices The “old fashioned” version just has 0 for no edge and 1 for edge b u – Integer key (index) associated with vertex 2 D-array adjacency array v 0 u w 1 0 0 2 CSC 401: Analysis of Algorithms 1 w 2 1 a 2 v b 11

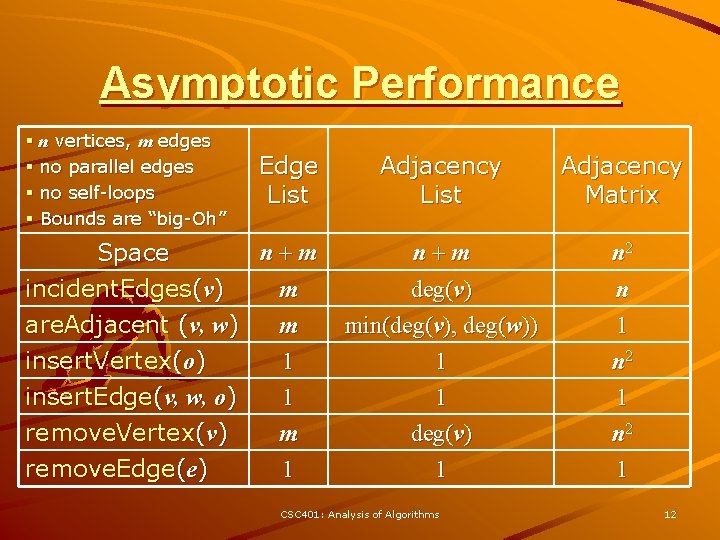
Asymptotic Performance § n vertices, m edges § no parallel edges § no self-loops § Bounds are “big-Oh” Edge List n+m Space incident. Edges(v) m are. Adjacent (v, w) m insert. Vertex(o) 1 insert. Edge(v, w, o) 1 remove. Vertex(v) remove. Edge(e) m 1 Adjacency List Adjacency Matrix n+m deg(v) min(deg(v), deg(w)) 1 n 2 n 1 n 2 1 deg(v) 1 1 n 2 1 CSC 401: Analysis of Algorithms 12

Trees and Forests A (free) tree is an undirected graph T such that – T is connected – T has no cycles This definition of tree is different from the one of a rooted tree A forest is an undirected graph without cycles The connected components of a forest are trees CSC 401: Analysis of Algorithms Tree Forest 13

Spanning Trees and Forests A spanning tree of a connected graph is a spanning subgraph that is a tree A spanning tree is not unique unless the graph is a tree Spanning trees have applications to the design of communication networks A spanning forest of a graph is a spanning subgraph that is a forest CSC 401: Analysis of Algorithms Graph Spanning tree 14

Depth-First Search Depth-first search (DFS) is a general technique for traversing a graph A DFS traversal of a graph G DFS on a graph with n vertices and m edges takes O(n + m ) time DFS can be further extended to solve other graph problems – Visits all the vertices and edges of G – Determines whether G is connected – Computes the connected components of G – Computes a spanning forest of G – Find and report a path between two given vertices – Find a cycle in the graph Depth-first search is to graphs what Euler tour is to binary trees CSC 401: Analysis of Algorithms 15

DFS Algorithm The algorithm uses a mechanism for setting and getting “labels” of vertices and edges Algorithm DFS(G) Input graph G Output labeling of the edges of G as discovery edges and back edges for all u G. vertices() set. Label(u, UNEXPLORED) for all e G. edges() set. Label(e, UNEXPLORED) for all v G. vertices() if get. Label(v) = UNEXPLORED DFS(G, v) Algorithm DFS(G, v) Input graph G and a start vertex v of G Output labeling of the edges of G in the connected component of v as discovery edges and back edges set. Label(v, VISITED) for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) DFS(G, w) else set. Label(e, BACK) CSC 401: Analysis of Algorithms 16

Properties of DFS Property 1 DFS(G, v) visits all the vertices and edges in the connected component of v A Property 2 The discovery edges labeled by DFS(G, v) form a spanning tree of the connected component of v B CSC 401: Analysis of Algorithms D E C 17

Analysis of DFS Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice – once as UNEXPLORED – once as VISITED Each edge is labeled twice – once as UNEXPLORED – once as DISCOVERY or BACK Method incident. Edges is called once for each vertex DFS runs in O(n + m) time provided the graph is represented by the adjacency list structure – Recall that Sv deg(v) = 2 m CSC 401: Analysis of Algorithms 18

We can specialize the DFS algorithm to find a path between two given vertices u and z Algorithm path. DFS(G, v, z) set. Label(v, VISITED) using the template S. push(v) method pattern if v = z We call DFS(G, u) with u return S. elements() as the start vertex for all e G. incident. Edges(v) We use a stack S to if get. Label(e) = UNEXPLORED keep track of the path w opposite(v, e) if get. Label(w) = UNEXPLORED between the start set. Label(e, DISCOVERY) vertex and the current S. push(e) vertex path. DFS(G, w, z) As soon as destination S. pop(e) vertex z is else encountered, we return set. Label(e, BACK) the path as the S. pop(v) contents of the stack CSC 401: Analysis of Algorithms 19 Path Finding

Cycle Finding We can specialize the Algorithm cycle. DFS(G, v, z) DFS algorithm to find a set. Label(v, VISITED) simple cycle using the S. push(v) template method for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED pattern w opposite(v, e) We use a stack S to S. push(e) keep track of the path if get. Label(w) = UNEXPLORED between the start set. Label(e, DISCOVERY) path. DFS(G, w, z) vertex and the current S. pop(e) vertex else As soon as a back edge T new empty stack repeat (v, w) is encountered, o S. pop() we return the cycle as T. push(o) the portion of the stack until o = w from the top to vertex w return T. elements() S. pop(v) CSC 401: Analysis of Algorithms 20

Breadth-First Search Breadth-first search (BFS) is a general technique for traversing a graph A BFS traversal of a graph G – Visits all the vertices and edges of G – Determines whether G is connected – Computes the connected components of G – Computes a spanning forest of G BFS on a graph with n vertices and m edges takes O(n + m ) time BFS can be further extended to solve other graph problems – Find and report a path with the minimum number of edges between two given vertices – Find a simple cycle, if there is one CSC 401: Analysis of Algorithms 21

BFS Algorithm The algorithm uses a mechanism for setting and getting “labels” of vertices and edges Algorithm BFS(G, s) L 0 new empty sequence L 0. insert. Last(s) set. Label(s, VISITED) i 0 while Li. is. Empty() Li +1 new empty sequence for all v Li. elements() for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = Algorithm BFS(G) Input graph G Output labeling of the edges and partition of the vertices of G for all u G. vertices() UNEXPLORED set. Label(u, UNEXPLORED) set. Label(e, DISCOVERY) for all e G. edges() set. Label(w, VISITED) set. Label(e, UNEXPLORED) Li +1. insert. Last(w) for all v G. vertices() else if get. Label(v) = UNEXPLORED set. Label(e, CROSS) i i +1 BFS(G, v) CSC 401: Analysis of Algorithms 22

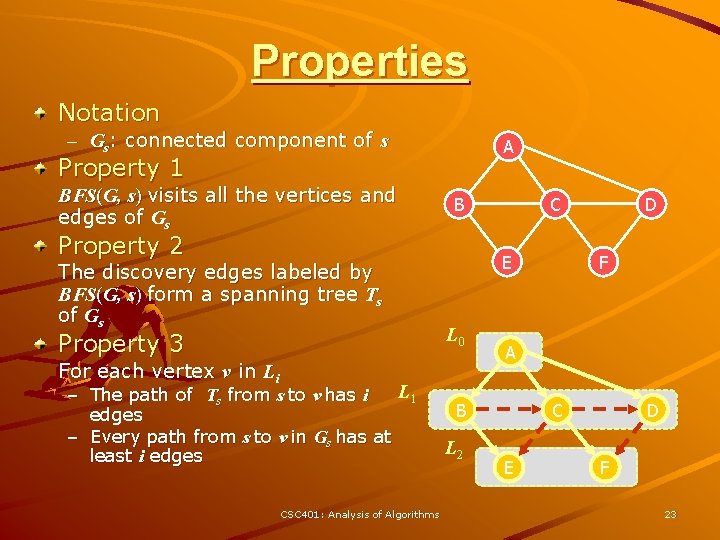
Properties Notation – Gs: connected component of s A Property 1 BFS(G, s) visits all the vertices and edges of Gs B Property 2 The discovery edges labeled by BFS(G, s) form a spanning tree Ts of Gs Property 3 E L 0 For each vertex v in Li L 1 – The path of Ts from s to v has i edges – Every path from s to v in Gs has at least i edges CSC 401: Analysis of Algorithms C F A B L 2 D C E D F 23

Analysis Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice – once as UNEXPLORED – once as VISITED Each edge is labeled twice – once as UNEXPLORED – once as DISCOVERY or CROSS Each vertex is inserted once into a sequence Li Method incident. Edges is called once for each vertex BFS runs in O(n + m) time provided the graph is represented by the adjacency list structure – Recall that Sv deg(v) = 2 m CSC 401: Analysis of Algorithms 24

Applications Using the template method pattern, we can specialize the BFS traversal of a graph G to solve the following problems in O(n + m) time – Compute the connected components of G – Compute a spanning forest of G – Find a simple cycle in G, or report that G is a forest – Given two vertices of G, find a path in G between them with the minimum number of edges, or report that no such path exists CSC 401: Analysis of Algorithms 25

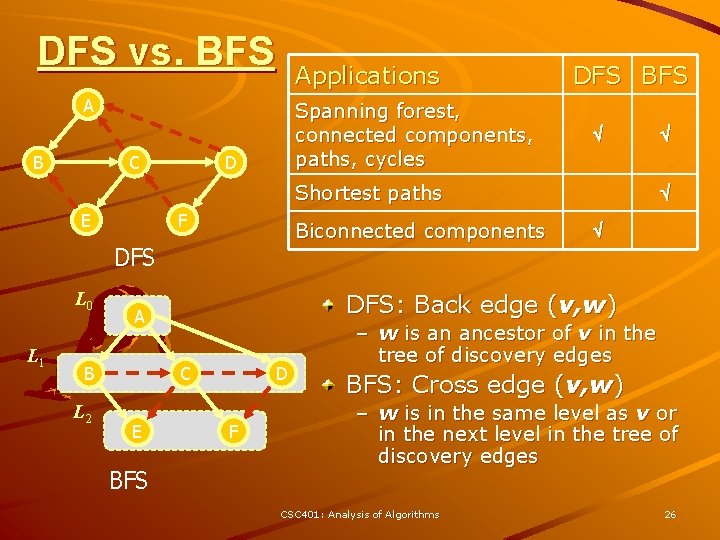
DFS vs. BFS Applications A B C Spanning forest, connected components, paths, cycles D DFS BFS Shortest paths E F Biconnected components DFS L 0 L 1 L 2 C E BFS DFS: Back edge (v, w) A B D F – w is an ancestor of v in the tree of discovery edges BFS: Cross edge (v, w) – w is in the same level as v or in the next level in the tree of discovery edges CSC 401: Analysis of Algorithms 26

Separation Edges and Vertices Definitions -- Let G be a connected graph – A separation edge of G is an edge whose removal disconnects G – A separation vertex of G is a vertex whose removal disconnects G Applications – Separation edges and vertices represent single points of failure in a network and are critical to the operation of the network Example – DFW, LGA and LAX are separation vertices – (DFW, LAX) is a separation edge SFO ORD PVD LGA HNL LAX DFW CSC 401: Analysis of Algorithms MIA 27

Biconnected Graph Equivalent definitions of a biconnected graph G – Graph G has no separation edges and no separation vertices – For any two vertices u and v of G, there are two disjoint simple paths between u and v (i. e. , two simple paths between u and v that share no other vertices or edges) – For any two vertices u and v of G, there is a simple cycle containing u and v Example SFO PVD ORD LGA HNL LAX DFW CSC 401: Analysis of Algorithms MIA 28

Biconnected Components Biconnected component of a graph G – A maximal biconnected subgraph of G, or – A subgraph consisting of a separation edge of G and its end vertices Interaction of biconnected components – An edge belongs to exactly one biconnected component – A nonseparation vertex belongs to exactly one biconnected component – A separation vertex belongs to two or more biconnected components Example of a graph with four biconnected components SFO ORD LGA HNL LAX DFW CSC 401: Analysis of Algorithms PVD RDU MIA 29

Equivalence Classes Given a set S, a relation R on S is a set of ordered pairs of elements of S, i. e. , R is a subset of S S An equivalence relation R on S satisfies the following properties Reflexive: (x, x) R Symmetric: (x, y) R (y, x) R Transitive: (x, y) R (y, z) R (x, z) R An equivalence relation R on S induces a partition of the elements of S into equivalence classes Example (connectivity relation among the vertices of a graph): – Let V be the set of vertices of a graph G – Define the relation C = {(v, w) V V such that G has a path from v to w} – Relation C is an equivalence relation – The equivalence classes of relation C are the vertices in each connected component of graph G CSC 401: Analysis of Algorithms 30

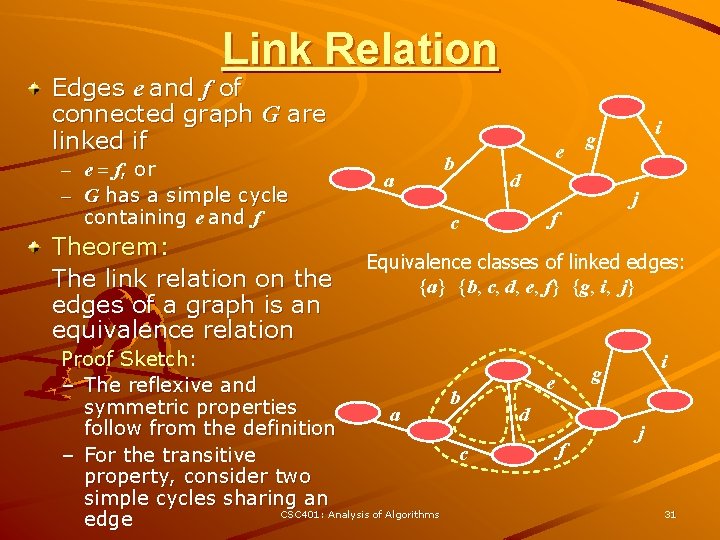
Link Relation Edges e and f of connected graph G are linked if – e = f, or – G has a simple cycle containing e and f Theorem: The link relation on the edges of a graph is an equivalence relation a b e d j f c i g Equivalence classes of linked edges: {a} {b, c, d, e, f} {g, i, j} Proof Sketch: – The reflexive and b symmetric properties a follow from the definition c – For the transitive property, consider two simple cycles sharing an CSC 401: Analysis of Algorithms edge i g e d f j 31

Link Components The link components of a connected graph G are the equivalence classes of edges with respect to the link relation A biconnected component of G is the subgraph of G induced by an equivalence class of linked edges A separation edge is a single-element equivalence class of linked edges A separation vertex has incident edges in at least two distinct equivalence classes of linked edge SFO ORD PVD LGA HNL LAX DFW CSC 401: Analysis of Algorithms RDU MIA 32

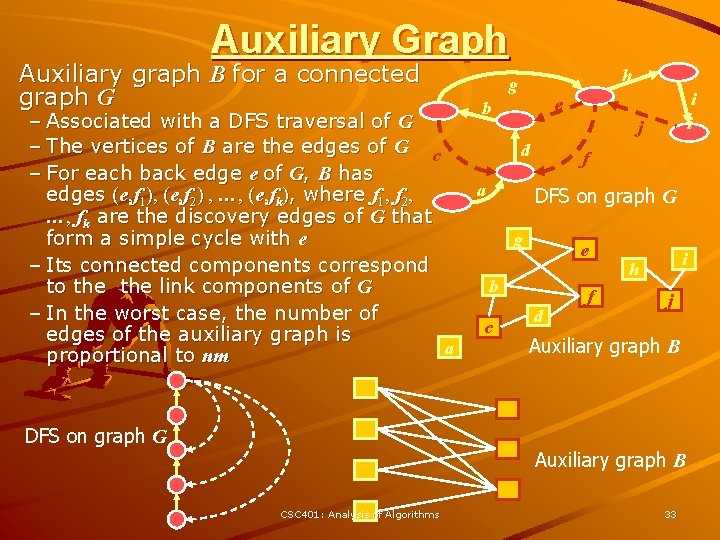
Auxiliary Graph Auxiliary graph B for a connected graph G – Associated with a DFS traversal of G – The vertices of B are the edges of G c – For each back edge e of G, B has edges (e, f 1), (e, f 2) , …, (e, fk), where f 1, f 2, …, fk are the discovery edges of G that form a simple cycle with e – Its connected components correspond to the link components of G – In the worst case, the number of edges of the auxiliary graph is a proportional to nm DFS on graph G h g i i e b j d a f DFS on graph G g e b c d f i h j Auxiliary graph B CSC 401: Analysis of Algorithms 33

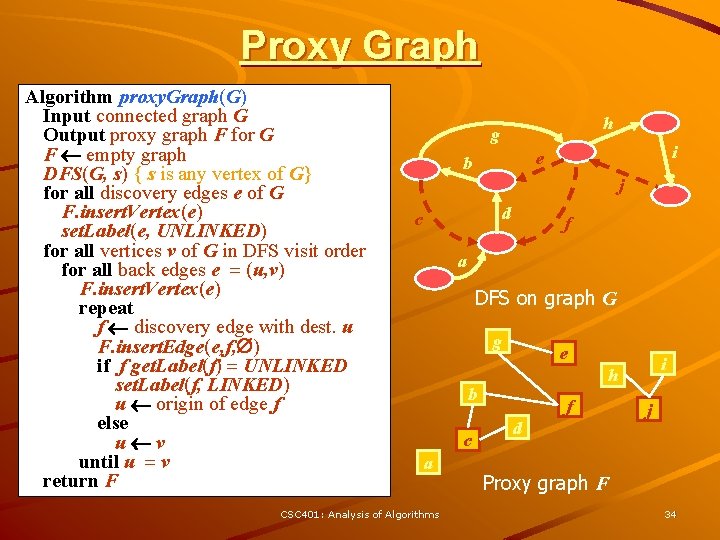
Proxy Graph Algorithm proxy. Graph(G) Input connected graph G Output proxy graph F for G F empty graph DFS(G, s) { s is any vertex of G} for all discovery edges e of G F. insert. Vertex(e) set. Label(e, UNLINKED) for all vertices v of G in DFS visit order for all back edges e = (u, v) F. insert. Vertex(e) repeat f discovery edge with dest. u F. insert. Edge(e, f, ) if f get. Label(f) = UNLINKED set. Label(f, LINKED) u origin of edge f else u v { ends the loop } until u = v return F h g i e b i j d c f a DFS on graph G g e b c a CSC 401: Analysis of Algorithms i h f d j Proxy graph F 34

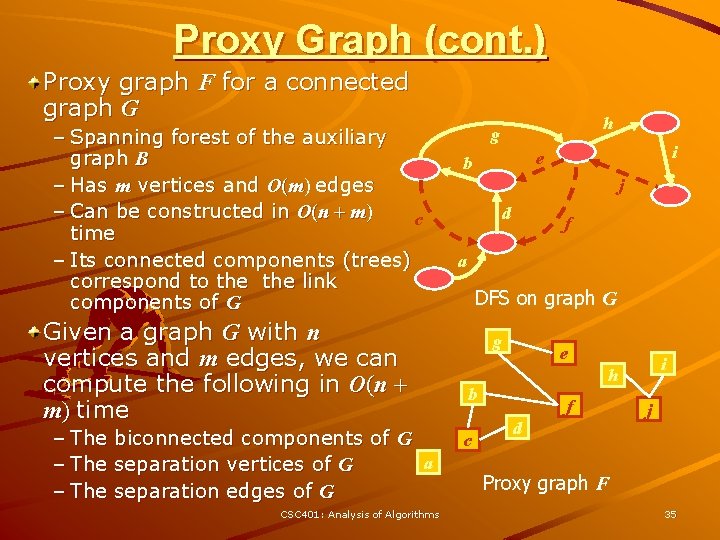
Proxy Graph (cont. ) Proxy graph F for a connected graph G – Spanning forest of the auxiliary graph B – Has m vertices and O(m) edges – Can be constructed in O(n + m) c time – Its connected components (trees) correspond to the link components of G Given a graph G with n vertices and m edges, we can compute the following in O(n + m) time – The biconnected components of G a separation vertices of G separation edges of G CSC 401: Analysis of Algorithms h g i e b i j d f a DFS on graph G g e b c i h f d j Proxy graph F 35

Digraphs A digraph is a graph whose edges are all directed – Short for “directed graph” Applications – one-way streets – flights – task scheduling E D C B A Properties: A graph G=(V, E) – Each edge goes in one direction: Edge (a, b) goes from a to b, but not b to a. – If G is simple, m < n*(n-1). – If we keep in-edges and out-edges in separate adjacency lists, we can perform listing of in-edges and out-edges in time proportional to their size. CSC 401: Analysis of Algorithms 36

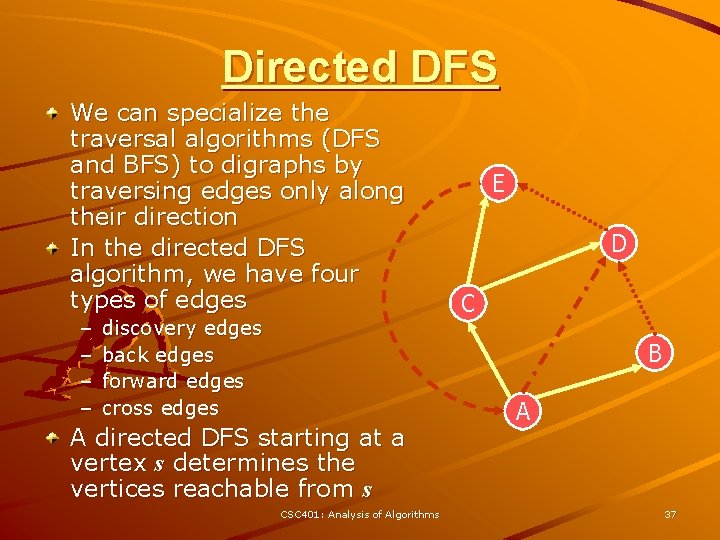
Directed DFS We can specialize the traversal algorithms (DFS and BFS) to digraphs by traversing edges only along their direction In the directed DFS algorithm, we have four types of edges – – discovery edges back edges forward edges cross edges E D C B A directed DFS starting at a vertex s determines the vertices reachable from s CSC 401: Analysis of Algorithms A 37

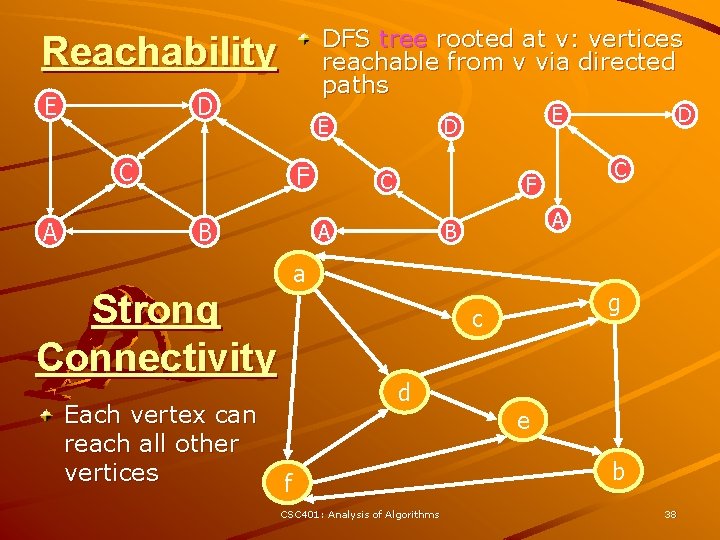
DFS tree rooted at v: vertices reachable from v via directed paths Reachability E D E C A F B C A B a g c d f CSC 401: Analysis of Algorithms D C F A Strong Connectivity Each vertex can reach all other vertices E D e b 38

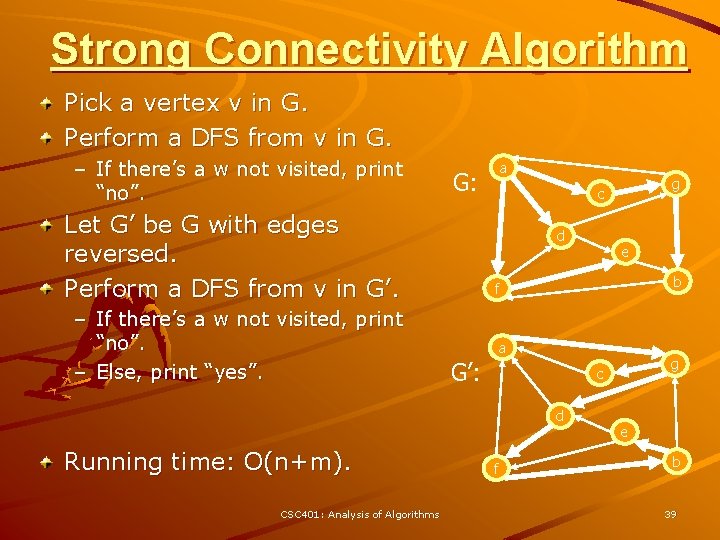
Strong Connectivity Algorithm Pick a vertex v in G. Perform a DFS from v in G. – If there’s a w not visited, print “no”. G: Let G’ be G with edges reversed. Perform a DFS from v in G’. – If there’s a w not visited, print “no”. – Else, print “yes”. a d CSC 401: Analysis of Algorithms e b f a G’: g c d Running time: O(n+m). g c f e b 39

Strongly Connected Components Maximal subgraphs such that each vertex can reach all other vertices in the subgraph Can also be done in O(n+m) time using DFS, but is more complicated (similar to biconnectivity). a g c d f e b CSC 401: Analysis of Algorithms {a, c, g} {f, d, e, b} 40

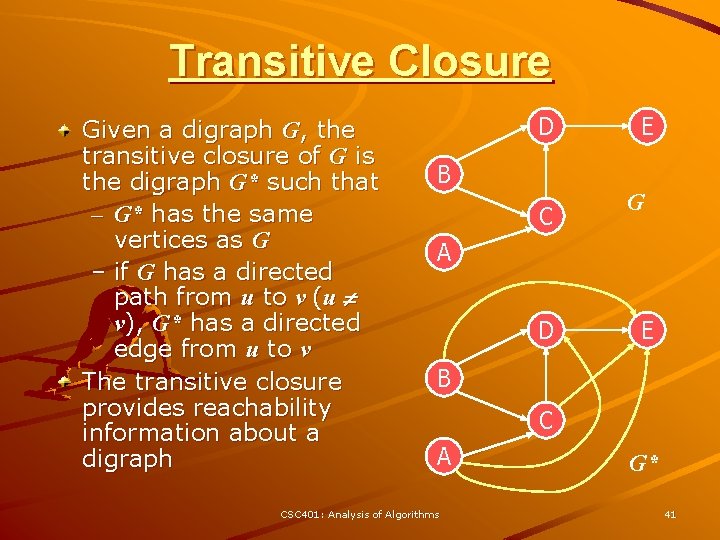
Transitive Closure Given a digraph G, the transitive closure of G is the digraph G* such that – G* has the same vertices as G – if G has a directed path from u to v (u v), G* has a directed edge from u to v The transitive closure provides reachability information about a digraph D E B C G A D E B C A CSC 401: Analysis of Algorithms G* 41

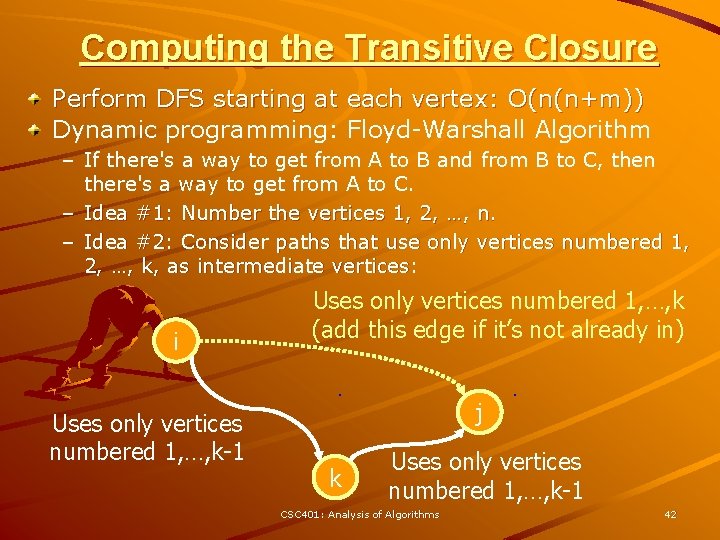
Computing the Transitive Closure Perform DFS starting at each vertex: O(n(n+m)) Dynamic programming: Floyd-Warshall Algorithm – If there's a way to get from A to B and from B to C, then there's a way to get from A to C. – Idea #1: Number the vertices 1, 2, …, n. – Idea #2: Consider paths that use only vertices numbered 1, 2, …, k, as intermediate vertices: i Uses only vertices numbered 1, …, k-1 Uses only vertices numbered 1, …, k (add this edge if it’s not already in) j k Uses only vertices numbered 1, …, k-1 CSC 401: Analysis of Algorithms 42

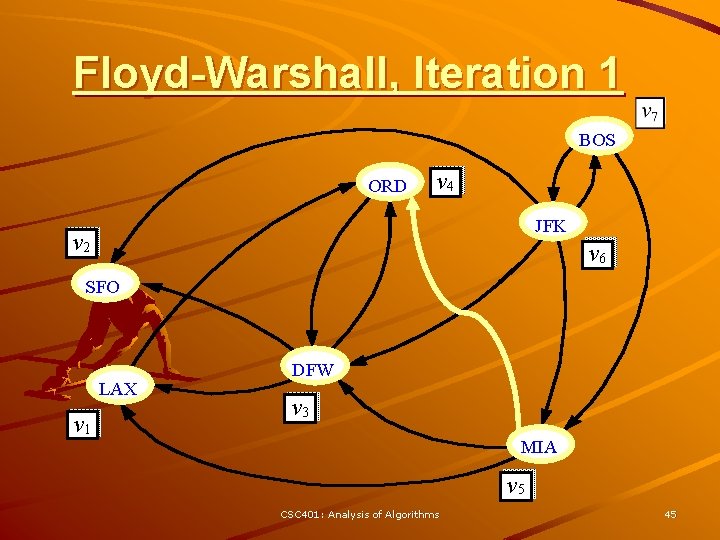
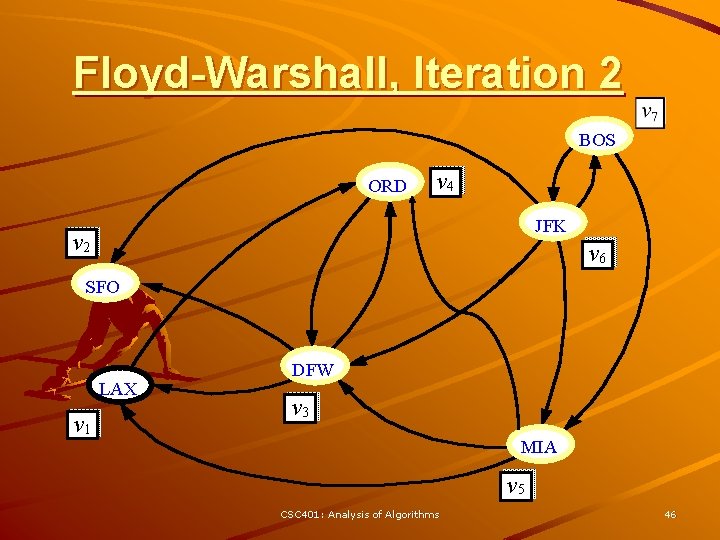
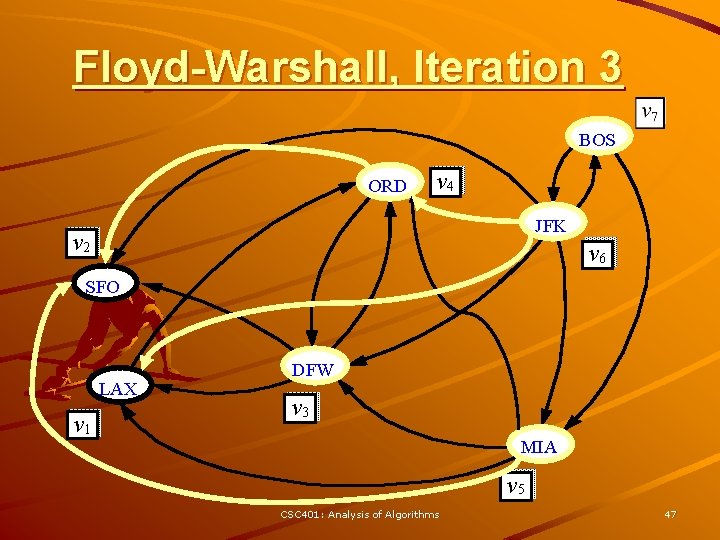
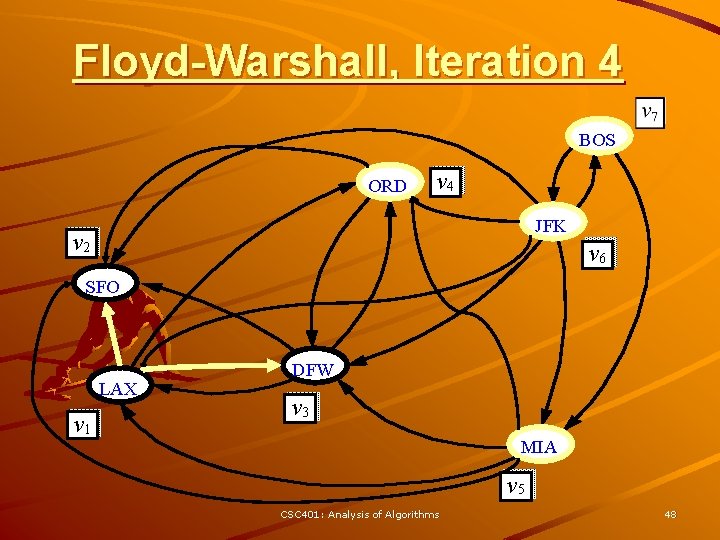
Floyd-Warshall’s Algorithm Floyd-Warshall’s algorithm numbers the vertices of G as v 1 , …, vn and computes a series of digraphs G 0, …, Gn Algorithm Floyd. Warshall(G) Input digraph G Output transitive closure G* of G i 1 for all v G. vertices() denote v as vi – G 0 = G i i+1 – Gk has a directed edge (vi, G 0 G vj) if G has a directed path for k 1 to n do from vi to vj with Gk - 1 intermediate vertices in for i 1 to n (i k) do the set {v 1 , …, vk} for j 1 to n (j i, k) do We have that Gn = G* if Gk - 1. are. Adjacent(vi, vk) In phase k, digraph Gk is Gk - 1. are. Adjacent(vk, vj) computed from Gk - 1 if Gk. are. Adjacent(vi, vj) 3 Running time: O(n ), Gk. insert. Directed. Edge(vi, vj , k) assuming are. Adjacent is return Gn O(1) (e. g. , adjacency matrix) CSC 401: Analysis of Algorithms 43

Floyd-Warshall Example BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 44

Floyd-Warshall, Iteration 1 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 45

Floyd-Warshall, Iteration 2 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 46

Floyd-Warshall, Iteration 3 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 47

Floyd-Warshall, Iteration 4 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 48

Floyd-Warshall, Iteration 5 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 49

Floyd-Warshall, Iteration 6 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 50

Floyd-Warshall, Conclusion BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 CSC 401: Analysis of Algorithms 51

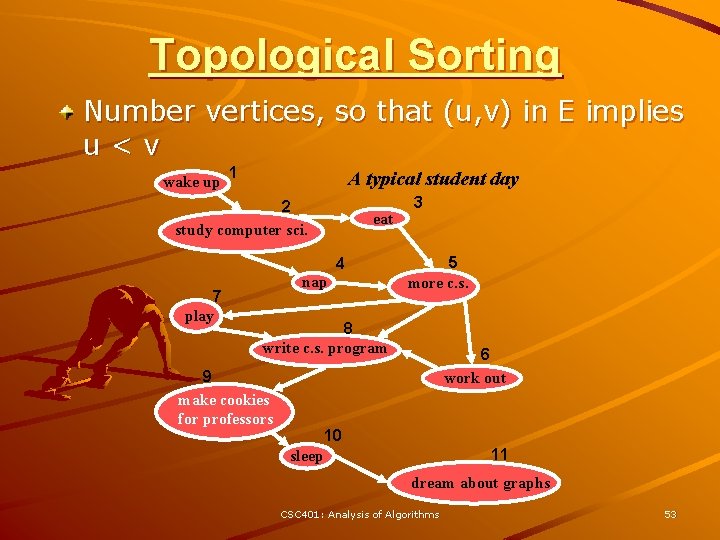
DAGs and Topological Ordering A directed acyclic graph (DAG) is a digraph that has no directed cycles A topological ordering of a digraph is a numbering v 1 , …, vn of the vertices such that for every edge (vi , vj), we have i < j Example: in a task scheduling digraph, a topological ordering a task sequence that satisfies the precedence constraints Theorem A digraph admits a topological ordering if and only if it is a DAG D E B C DAG G A v 2 v 1 D B C A CSC 401: Analysis of Algorithms v 4 E v 5 v 3 Topological ordering of G 52

Topological Sorting Number vertices, so that (u, v) in E implies u<v wake up 1 A typical student day 2 study computer sci. eat 4 7 play nap 3 5 more c. s. 8 write c. s. program 9 make cookies for professors 6 work out 10 11 sleep dream about graphs CSC 401: Analysis of Algorithms 53

Algorithm for Topological Sorting Note: This algorithm is different than the one in Goodrich-Tamassia Method Topological. Sort(G) H G // Temporary copy of G n G. num. Vertices() while H is not empty do Let v be a vertex with no outgoing edges Label v n n n-1 Remove v from H Running time: O(n + m). How…? CSC 401: Analysis of Algorithms 54

Topological Sorting Algorithm using DFS Simulate the algorithm by using depth-first search Algorithm topological. DFS(G) Input dag G Output topological ordering of G n G. num. Vertices() for all u G. vertices() set. Label(u, UNEXPLORED) for all e G. edges() set. Label(e, UNEXPLORED) for all v G. vertices() if get. Label(v) = UNEXPLORED topological. DFS(G, v) O(n+m) time. Algorithm topological. DFS(G, v) Input graph G and a start vertex v of G Output labeling of the vertices of G in the connected component of v set. Label(v, VISITED) for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) topological. DFS(G, w) else {e is a forward or cross edge} Label v with topological number n n n-1 CSC 401: Analysis of Algorithms 55