CSC 401 Analysis of Algorithms Chapter 7 Weighted

CSC 401 – Analysis of Algorithms Chapter 7 Weighted Graphs Objectives: • Introduce weighted graphs • Present shortest path problems, properties, and algorithms • Present algorithms to finding the shortest path for a given pair of vertices • Present various algorithms to finding the shortest paths for all pair of vertices • Introduce the minimum spanning tree (MST) and related algorithms CSC 401: Analysis of Algorithms 7 -1

Weighted Graphs In a weighted graph, each edge has an associated numerical value, called the weight of the edge Edge weights may represent, distances, costs, etc. Example: – In a flight route graph, the weight of an edge represents the distance in miles between the endpoint airports LAX 1 1233 ORD 1 7 138 DFW CSC 401: Analysis of Algorithms PVD 42 1205 337 HNL 2555 3 4 7 849 802 SFO 1843 LGA 1120 10 99 MIA 2

Shortest Path Problem Given a weighted graph and two vertices u and v, we want to find a path of minimum total weight between u and v. – Length of a path is the sum of the weights of its edges. Example: – Shortest path between Providence and Honolulu Applications Internet packet routing Flight reservations Driving directions SFO LAX 3 4 7 1 1233 849 ORD DFW CSC 401: Analysis of Algorithms 7 8 3 1 2 PVD 14 1205 337 HNL 2555 1843 802 – – – LGA 1120 10 99 MIA 3

Shortest Path Properties Property 1: A subpath of a shortest path is itself a shortest path Property 2: There is a tree of shortest paths from a start vertex to all the other vertices Example: Tree of shortest paths from Providence LAX 1233 DFW CSC 401: Analysis of Algorithms 7 8 3 1 2 PVD 14 1205 337 HNL 2555 3 4 17 849 ORD 802 SFO 1843 LGA 1120 10 99 MIA 4

Dijkstra’s Algorithm The distance of a vertex v from a vertex s is the length of a shortest path between s and v Dijkstra’s algorithm computes the distances of all the vertices from a given start vertex s Assumptions: We grow a “cloud” of vertices, beginning with s and eventually covering all the vertices We store with each vertex v a label d(v) representing the distance of v from s in the subgraph consisting of the cloud and its adjacent vertices At each step – We add to the cloud the vertex u outside the cloud with the smallest distance label, d(u) – We update the labels of the vertices adjacent to u CSC 401: Analysis of Algorithms 5 – the graph is connected – the edges are undirected – the edge weights are nonnegative

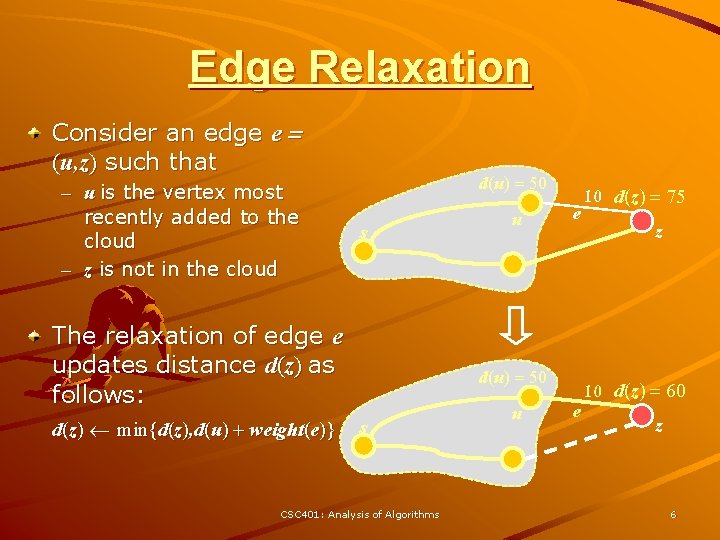
Edge Relaxation Consider an edge e = (u, z) such that – u is the vertex most recently added to the cloud – z is not in the cloud d(u) = 50 s The relaxation of edge e updates distance d(z) as follows: d(z) min{d(z), d(u) + weight(e)} u e d(u) = 50 s CSC 401: Analysis of Algorithms u e 10 d(z) = 75 z 10 d(z) = 60 z 6

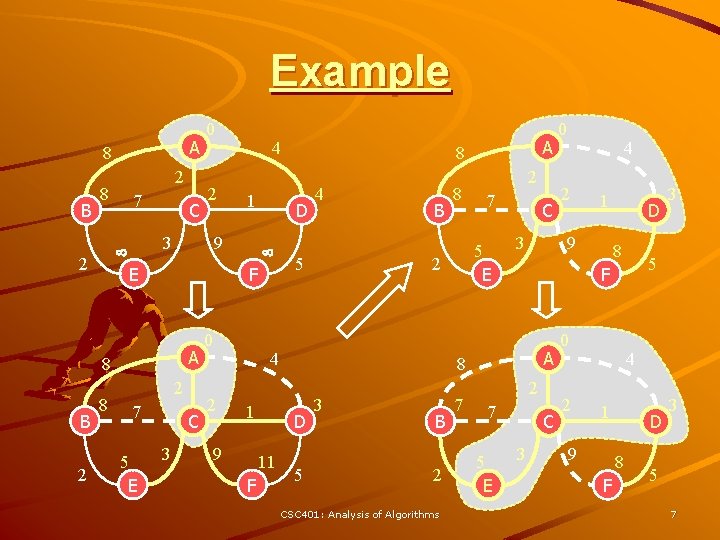
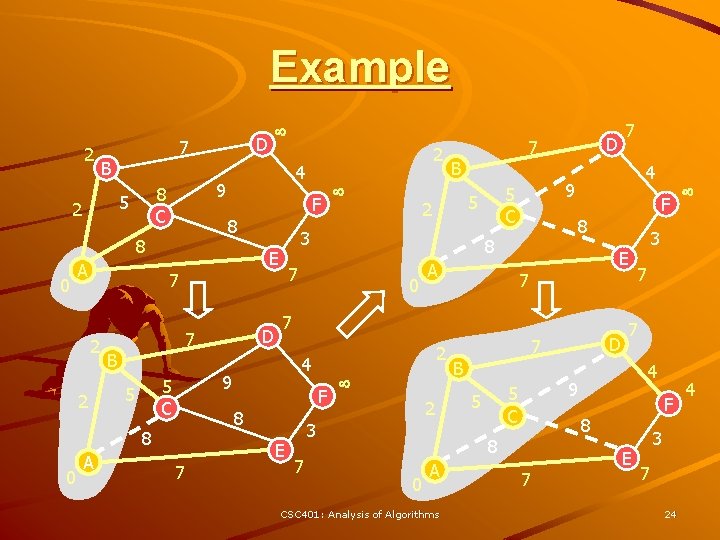
Example A 8 B 2 8 7 E 2 8 1 2 7 C 3 0 2 4 5 B 9 F 2 7 5 E C 3 5 3 B 2 CSC 401: Analysis of Algorithms 7 4 2 1 D 8 2 7 C 3 0 2 3 5 F A 5 E 0 9 8 D 11 8 2 4 1 A 8 D F A 5 E 4 9 8 B 2 3 2 C 0 4 1 9 D 8 F 3 5 7

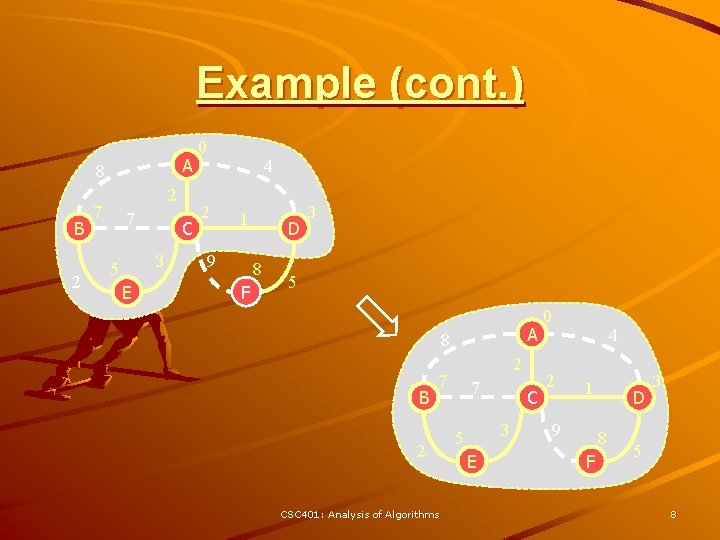
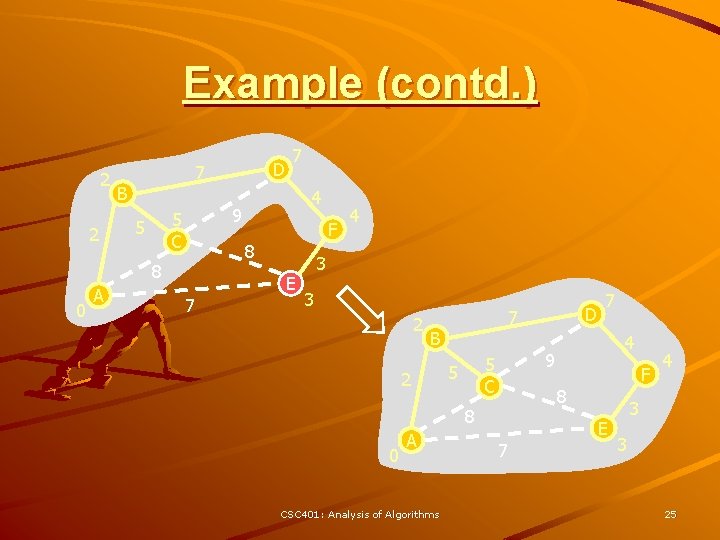
Example (cont. ) A 8 B 2 2 7 7 C 3 5 E 0 2 4 1 9 D 8 F 3 5 A 8 B 2 7 2 CSC 401: Analysis of Algorithms 7 C 3 5 E 0 2 4 1 9 D 8 F 3 5 8

Dijkstra’s Algorithm A priority queue stores Algorithm Dijkstra. Distances(G, s) Q new heap-based priority queue the vertices outside for all v G. vertices() the cloud if v = s – Key: distance – Element: vertex Locator-based methods – insert(k, e) returns a locator – replace. Key(l, k) changes the key of an item We store two labels with each vertex: – Distance (d(v) label) – locator in priority queue set. Distance(v, 0) else set. Distance(v, ) l Q. insert(get. Distance(v), v) set. Locator(v, l) while Q. is. Empty() u Q. remove. Min() for all e G. incident. Edges(u) { relax edge e } z G. opposite(u, e) r get. Distance(u) + weight(e) if r < get. Distance(z) set. Distance(z, r) Q. replace. Key(get. Locator(z), r) CSC 401: Analysis of Algorithms 9

Graph operations Analysis – Method incident. Edges is called once for each vertex Label operations – We set/get the distance and locator labels of vertex z O(deg(z)) times – Setting/getting a label takes O(1) time Priority queue operations – Each vertex is inserted once into and removed once from the priority queue, taking O(log n) time – The key of a vertex in the priority queue is modified at most deg(w) times, where each key change takes O(log n) time Dijkstra’s algorithm runs in O((n + m) log n) time provided the graph is represented by the adjacency list structure – Recall that Sv deg(v) = 2 m The running time: O(m log n) CSC 401: Analysis of Algorithms 10

Extension Using the template method pattern, we can extend Dijkstra’s algorithm to return a tree of shortest paths from the start vertex to all other vertices We store with each vertex a third label: – parent edge in the shortest path tree Algorithm Dijkstra. Shortest. Paths. Tree(G, s) … for all v G. vertices() … set. Parent(v, ) … for all e G. incident. Edges(u) { relax edge e } z G. opposite(u, e) r get. Distance(u) + weight(e) if r < get. Distance(z) set. Distance(z, r) set. Parent(z, e) Q. replace. Key(get. Locator(z), r) In the edge relaxation step, we update the parent label CSC 401: Analysis of Algorithms 11

Why Dijkstra’s Algorithm Works Dijkstra’s algorithm is based on the greedy method. It adds vertices by increasing distance. n n Suppose it didn’t find all shortest distances. Let F be the first wrong vertex the algorithm processed. When the previous node, D, on the true shortest path was considered, its distance was correct. But the edge (D, F) was relaxed at that time! Thus, so long as d(F)>d(D), F’s distance cannot be wrong. That is, there is no wrong vertex. CSC 401: Analysis of Algorithms A 8 B 2 2 7 7 C 3 5 E 0 2 4 1 9 D 8 F 3 5 12

Why It Doesn’t Work for Negative-Weight Edges Dijkstra’s algorithm is based on the greedy method. It adds vertices by increasing distance. – If a node with a negative incident edge were to be added late to the cloud, it could mess up distances for vertices already in the cloud. A 8 B 2 6 7 7 C 0 5 E 0 4 5 1 -8 D 9 F 4 5 C’s true distance is 1, but it is already in the cloud with d(C)=5! CSC 401: Analysis of Algorithms 13

Bellman-Ford Algorithm Works even with Algorithm Bellman. Ford(G, s) negative-weight edges for all v G. vertices() Must assume directed if v = s edges (for otherwise set. Distance(v, 0) we would have else negative-weight set. Distance(v, ) cycles) for i 1 to n-1 do Iteration i finds all for each e G. edges() shortest paths that { relax edge e } use i edges. u G. origin(e) Running time: O(nm). z G. opposite(u, e) Can be extended to r get. Distance(u) + weight(e) detect a negativeif r < get. Distance(z) weight cycle if it exists set. Distance(z, r) – How? CSC 401: Analysis of Algorithms 14

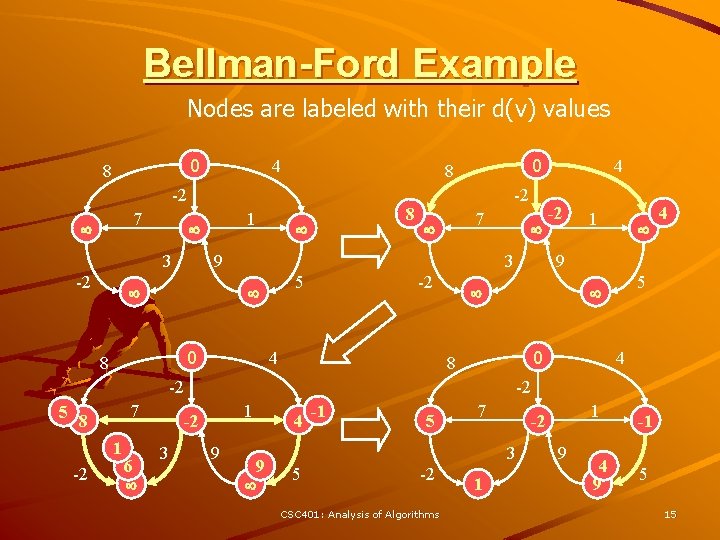
Bellman-Ford Example Nodes are labeled with their d(v) values 0 8 4 -2 7 3 -2 1 0 8 8 -2 7 9 3 5 0 8 -2 4 7 1 -2 6 1 5 4 9 0 8 4 -2 1 -2 3 -2 -2 5 8 4 9 9 4 -1 5 7 3 5 -2 CSC 401: Analysis of Algorithms 1 1 -2 9 4 9 -1 5 15

DAG-Based Algorithm Dag. Distances(G, s) Works even with for all v G. vertices() negative-weight if v = s edges set. Distance(v, 0) Uses topological else order set. Distance(v, ) Doesn’t use any Perform a topological sort of the vertices fancy data for u 1 to n do {in topological order} structures for each e G. out. Edges(u) Is much faster { relax edge e } than Dijkstra’s z G. opposite(u, e) algorithm r get. Distance(u) + weight(e) Running time: if r < get. Distance(z) O(n+m). set. Distance(z, r) CSC 401: Analysis of Algorithms 16

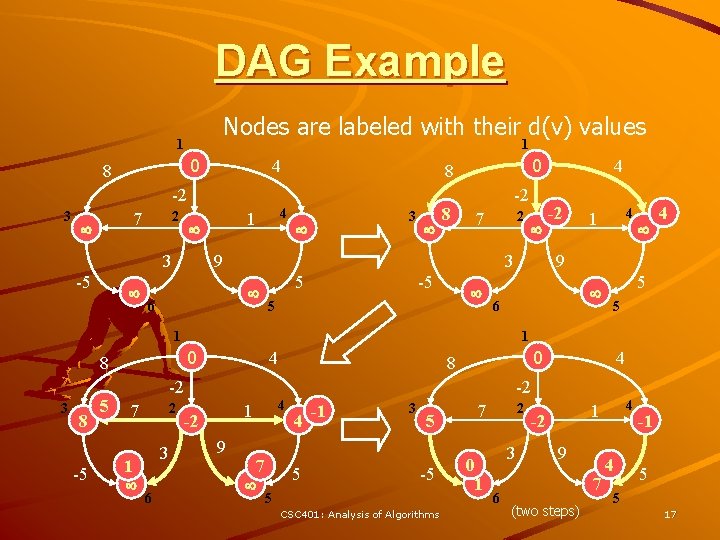
DAG Example Nodes are labeled with their d(v) values 1 1 0 8 4 -2 3 2 7 3 -5 4 1 0 8 3 8 -2 2 7 9 3 6 5 -5 5 0 8 -5 2 1 3 6 4 9 6 4 5 5 0 8 -2 7 4 1 1 8 5 -2 1 3 4 4 -2 4 1 -2 9 7 4 5 -1 3 5 -5 5 CSC 401: Analysis of Algorithms 2 7 0 1 3 6 4 1 -2 9 7 (two steps) 4 -1 5 5 17

All-Pairs Shortest Paths Find the distance between every pair of vertices in a weighted directed graph G. We can make n calls to Dijkstra’s algorithm (if no negative edges), which takes O(nmlog n) time. Likewise, n calls to Bellman-Ford would take O(n 2 m) time. We can achieve O(n 3) time using dynamic programming (similar to the Floyd-Warshall algorithm). Algorithm All. Pair(G) {assumes vertices 1, …, n} for all vertex pairs (i, j) if i = j D 0[i, i] 0 else if (i, j) is an edge in G D 0[i, j] weight of edge (i, j) else D 0[i, j] + for k 1 to n do for i 1 to n do for j 1 to n do Dk[i, j] min{Dk-1[i, j], Dk-1[i, k]+Dk-1[k, j]} return Dn Uses only vertices numbered 1, …, k (compute weight of this edge) j Uses only vertices k numbered 1, …, k-1 i CSC 401: Analysis of Algorithms 18

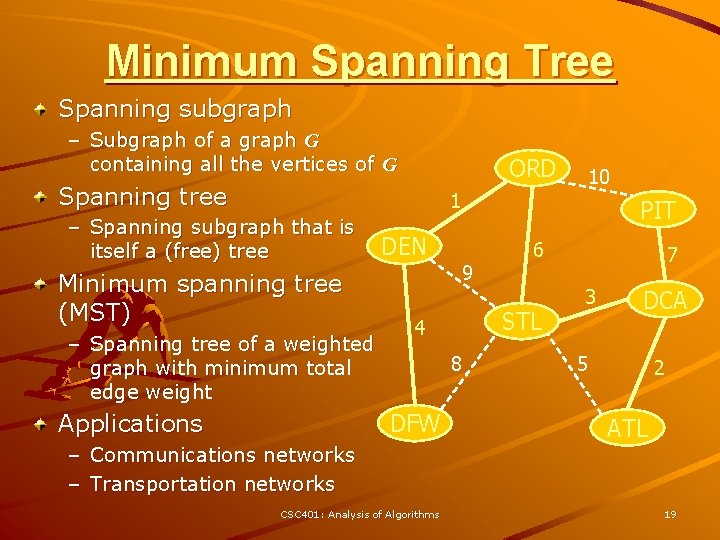
Minimum Spanning Tree Spanning subgraph – Subgraph of a graph G containing all the vertices of G ORD Spanning tree 10 1 – Spanning subgraph that is itself a (free) tree Minimum spanning tree (MST) – Spanning tree of a weighted graph with minimum total edge weight Applications DEN PIT 9 STL 4 8 DFW – Communications networks – Transportation networks CSC 401: Analysis of Algorithms 6 7 3 DCA 5 2 ATL 19

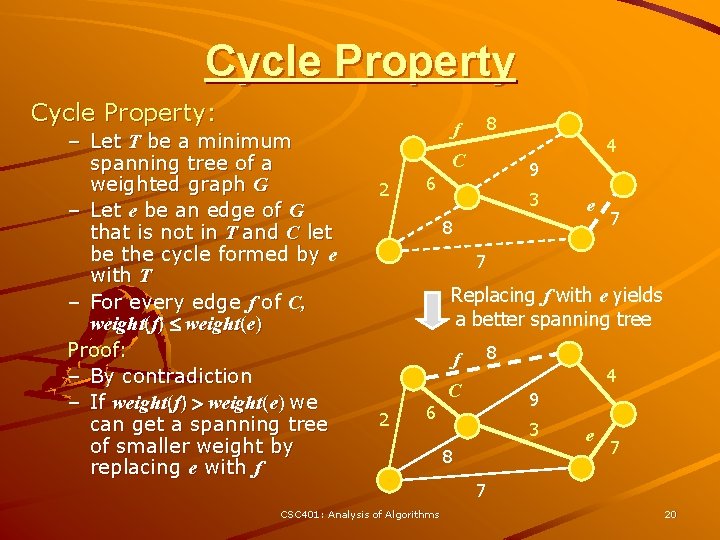
Cycle Property: – Let T be a minimum spanning tree of a weighted graph G – Let e be an edge of G that is not in T and C let be the cycle formed by e with T – For every edge f of C, weight(f) weight(e) Proof: – By contradiction – If weight(f) > weight(e) we can get a spanning tree of smaller weight by replacing e with f f 2 8 4 C 6 9 3 e 8 7 7 Replacing f with e yields a better spanning tree f 2 6 CSC 401: Analysis of Algorithms 8 4 C 9 3 8 e 7 7 20

Partition Property: U V Consider a partition of the vertices 7 f of G into subsets U and V 4 Let e be an edge of minimum 9 5 weight across the partition 2 8 There is a minimum spanning tree 3 of G containing edge e 8 e Proof: 7 Let T be an MST of G Replacing f with e yields If T does not contain e, consider another MST the cycle C formed by e with T and let f be an edge of C across the U V partition f 7 By the cycle property, 4 weight(f) weight(e) 9 5 Thus, weight(f) = weight(e) 2 8 We obtain another MST by 3 8 replacing f with e e 7 CSC 401: Analysis of Algorithms 21

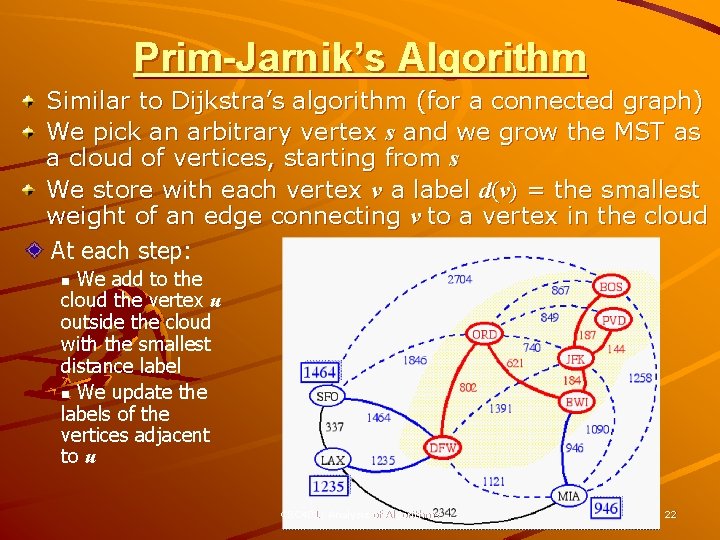
Prim-Jarnik’s Algorithm Similar to Dijkstra’s algorithm (for a connected graph) We pick an arbitrary vertex s and we grow the MST as a cloud of vertices, starting from s We store with each vertex v a label d(v) = the smallest weight of an edge connecting v to a vertex in the cloud At each step: We add to the cloud the vertex u outside the cloud with the smallest distance label n We update the labels of the vertices adjacent to u n CSC 401: Analysis of Algorithms 22

Prim-Jarnik’s Algorithm (cont. ) A priority queue stores Algorithm Prim. Jarnik. MST(G) the vertices outside Q new heap-based priority queue the cloud s a vertex of G – Key: distance – Element: vertex Locator-based methods – insert(k, e) returns a locator – replace. Key(l, k) changes the key of an item We store three labels with each vertex: – Distance – Parent edge in MST – Locator in priority queue for all v G. vertices() if v = s set. Distance(v, 0) else set. Distance(v, ) set. Parent(v, ) l Q. insert(get. Distance(v), v) set. Locator(v, l) while Q. is. Empty() u Q. remove. Min() for all e G. incident. Edges(u) z G. opposite(u, e) r weight(e) if r < get. Distance(z) set. Distance(z, r) set. Parent(z, e) Q. replace. Key(get. Locator(z), r) CSC 401: Analysis of Algorithms 23

Example 2 7 B 0 2 B 5 C 0 2 0 A 4 9 5 C 5 F 8 8 7 E 7 7 2 4 F 8 7 B 7 D 7 3 9 8 A D 7 5 F E 7 2 2 4 8 8 A 9 8 C 5 2 D E 2 3 7 7 B 0 CSC 401: Analysis of Algorithms 3 7 7 4 9 5 C 5 F 8 8 A D 7 E 3 7 24 4

Example (contd. ) 2 2 B 0 4 9 5 C 5 F 8 8 A D 7 7 7 E 4 3 3 2 B 2 0 CSC 401: Analysis of Algorithms 4 9 5 C 5 F 8 8 A D 7 7 7 E 4 3 3 25

Analysis Graph operations – Method incident. Edges is called once for each vertex Label operations – We set/get the distance, parent and locator labels of vertex z O(deg(z)) times – Setting/getting a label takes O(1) time Priority queue operations – Each vertex is inserted once into and removed once from the priority queue, where each insertion or removal takes O(log n) time – The key of a vertex w in the priority queue is modified at most deg(w) times, where each key change takes O(log n) time Prim-Jarnik’s algorithm runs in O((n + m) log n) time provided the graph is represented by the adjacency list structure – Recall that Sv deg(v) = 2 m The running time is O(m log n) since the graph is connected CSC 401: Analysis of Algorithms 26

Kruskal’s Algorithm Kruskal. MST(G) for each vertex V in G do define a Cloud(v) of {v} let Q be a priority queue. n Key: weight Insert all edges into Q using their n Element: edge weights as the key At the end of the T algorithm while T has fewer than n-1 edges do n We are left with one edge e = T. remove. Min() cloud that Let u, v be the endpoints of e encompasses the MST if Cloud(v) Cloud(u) then n A tree T which is our Add edge e to T MST Merge Cloud(v) and Cloud(u) return T A priority queue stores the edges outside the cloud CSC 401: Analysis of Algorithms 27

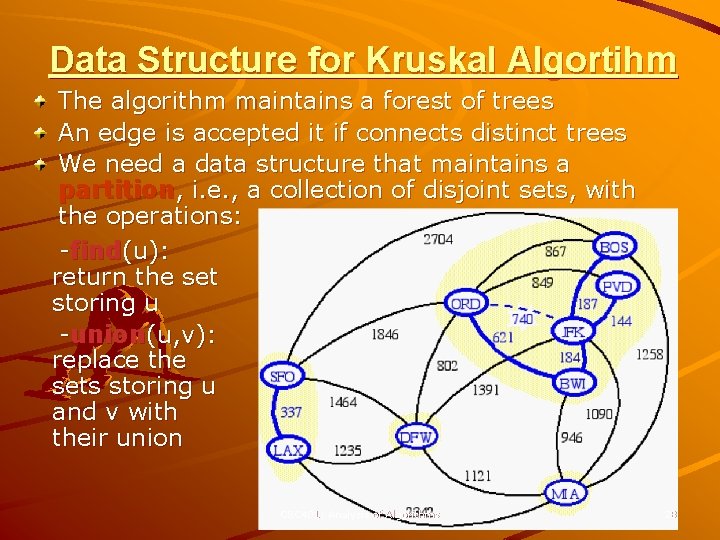
Data Structure for Kruskal Algortihm The algorithm maintains a forest of trees An edge is accepted it if connects distinct trees We need a data structure that maintains a partition, i. e. , a collection of disjoint sets, with the operations: -find(u): return the set storing u -union(u, v): replace the sets storing u and v with their union CSC 401: Analysis of Algorithms 28

Representation of a Partition Each set is stored in a sequence Each element has a reference back to the set – operation find(u) takes O(1) time, and returns the set of which u is a member. – in operation union(u, v), we move the elements of the smaller set to the sequence of the larger set and update their references – the time for operation union(u, v) is min(nu, nv), where nu and nv are the sizes of the sets storing u and v Whenever an element is processed, it goes into a set of size at least double, hence each element is processed at most log n times CSC 401: Analysis of Algorithms 29

Partition-Based Implementation A partition-based version of Kruskal’s Algorithm performs cloud merges as unions and tests as finds. Algorithm Kruskal(G): Input: A weighted graph G. Output: An MST T for G. Let P be a partition of the vertices of G, where each vertex forms a separate set. Let Q be a priority queue storing the edges of G, sorted by their weights Let T be an initially-empty tree while Q is not empty do (u, v) Q. remove. Min. Element() Running time: if P. find(u) != P. find(v) then O((n+m)log n) Add (u, v) to T P. union(u, v) return T CSC 401: Analysis of Algorithms 30

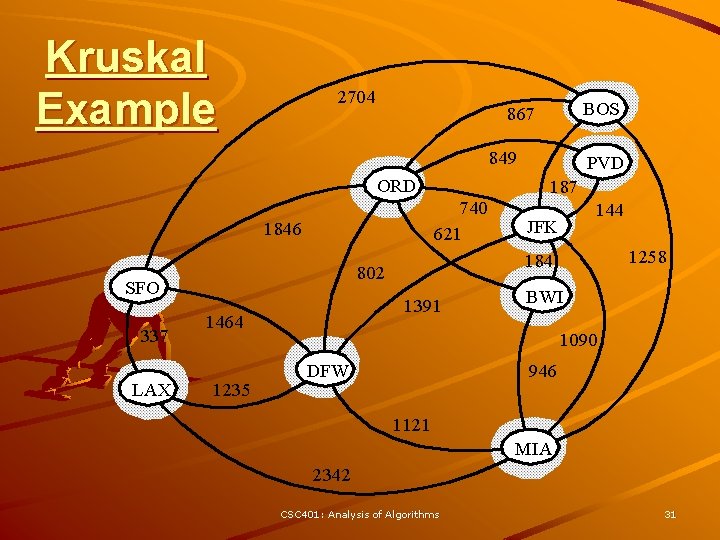
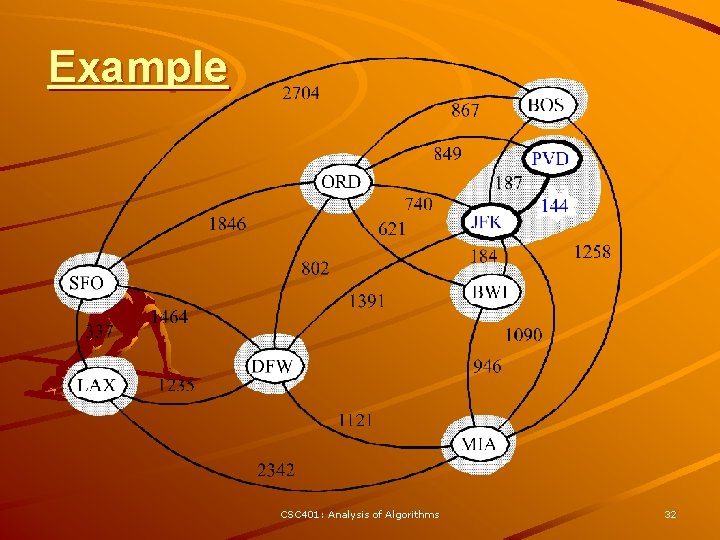
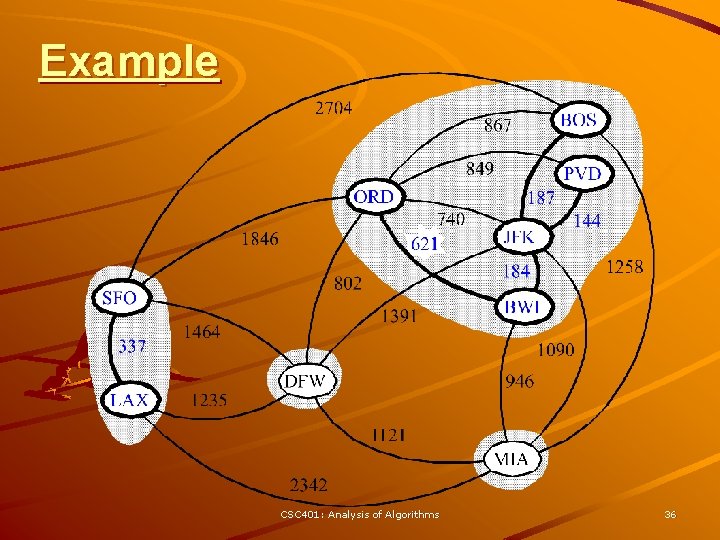
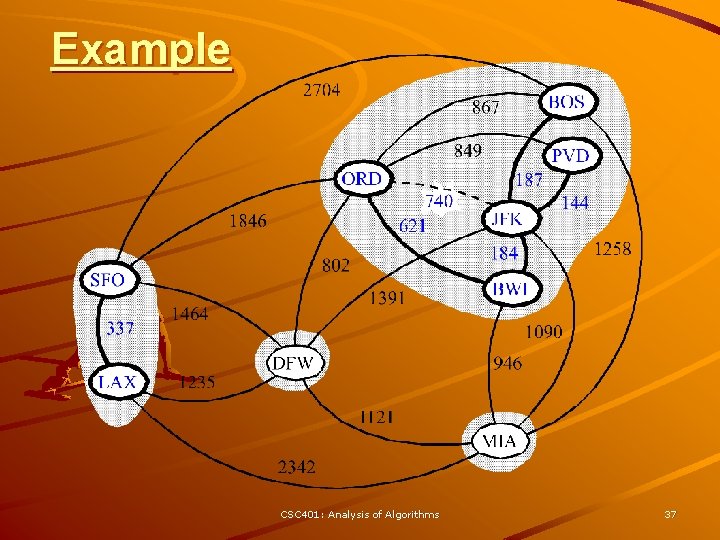
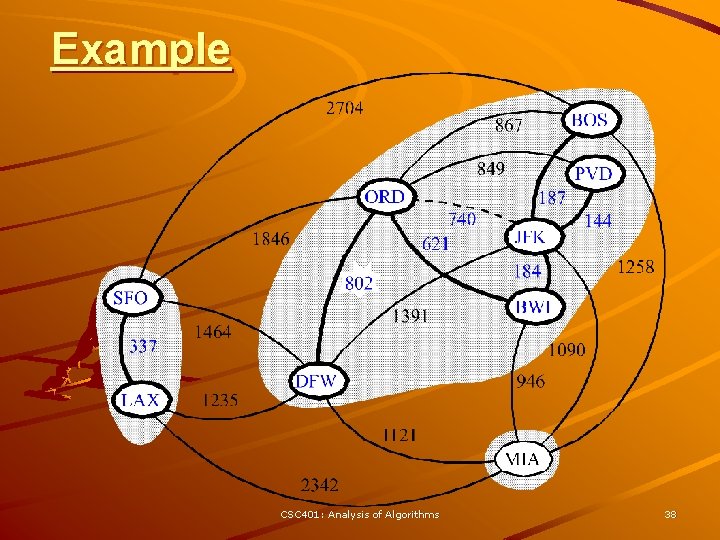
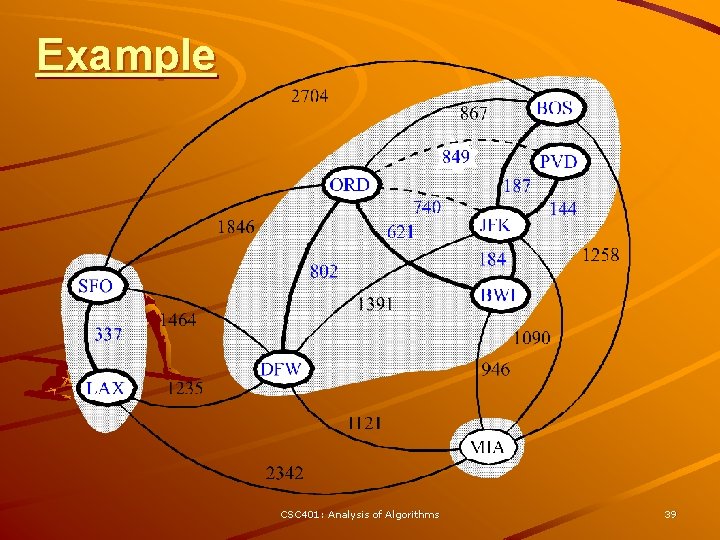
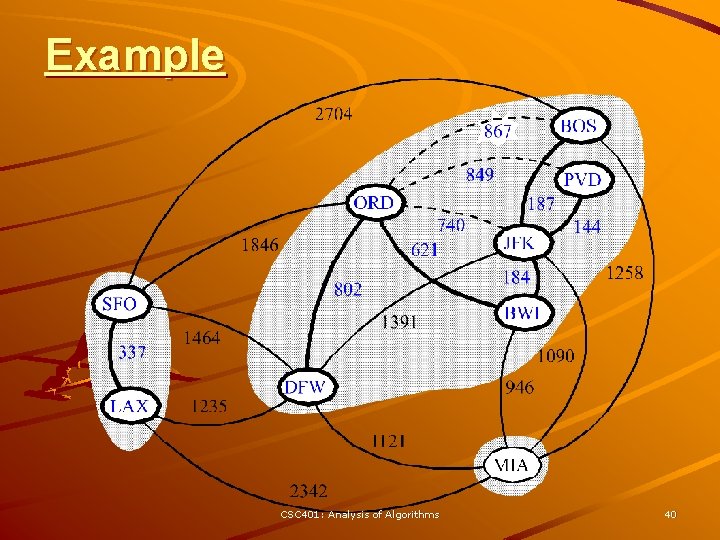
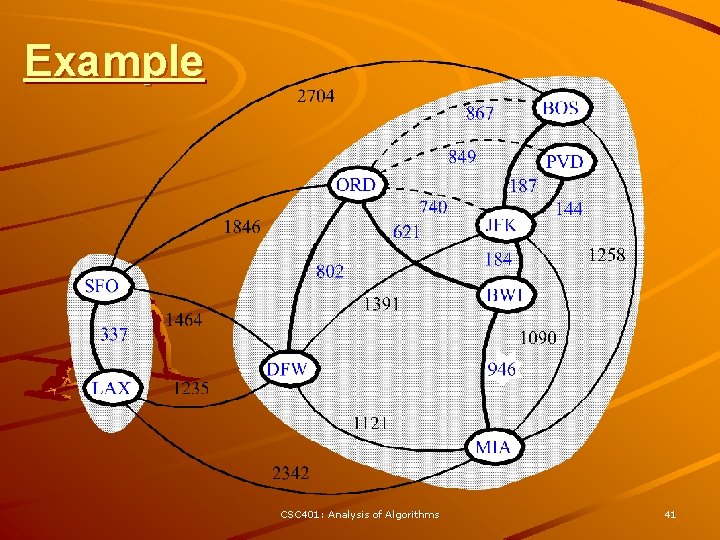
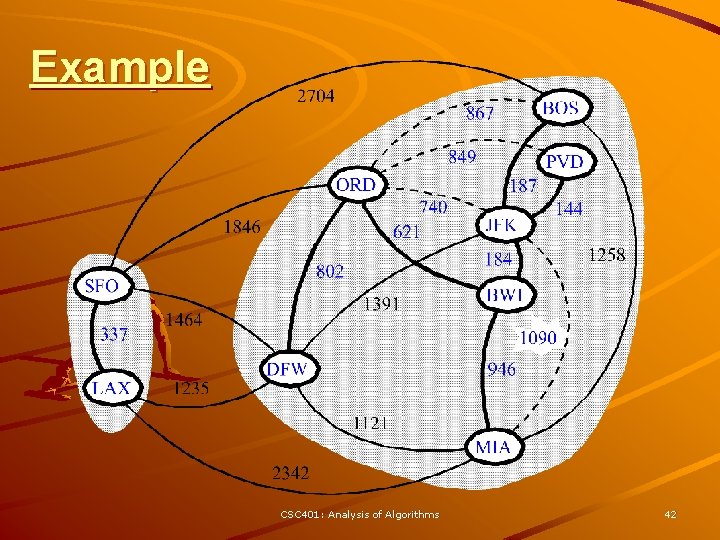
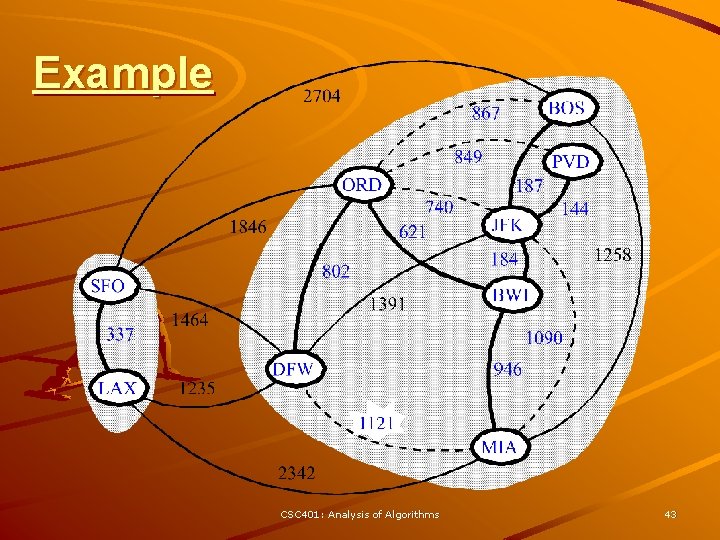
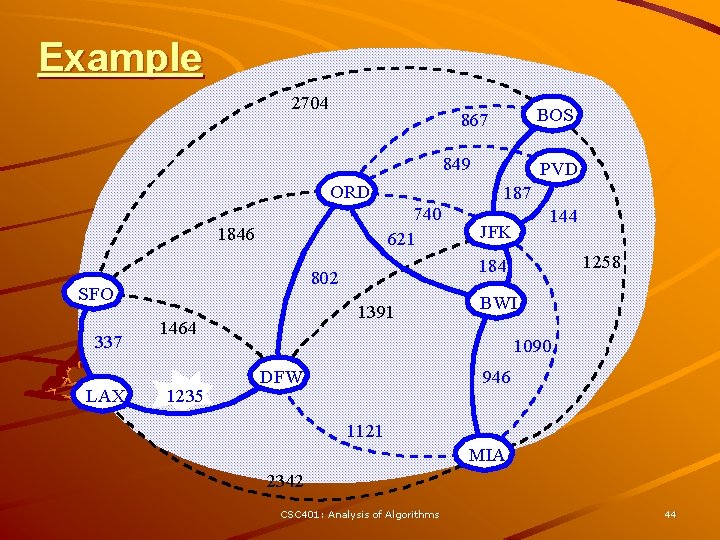
Kruskal Example 2704 BOS 867 849 ORD 740 621 1846 337 LAX 1391 1464 1235 187 144 JFK 1258 184 802 SFO PVD BWI 1090 DFW 946 1121 MIA 2342 CSC 401: Analysis of Algorithms 31

Example CSC 401: Analysis of Algorithms 32

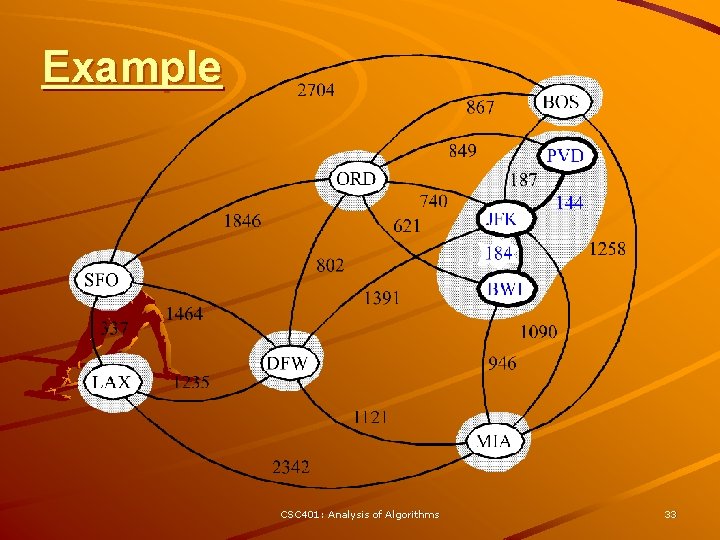
Example CSC 401: Analysis of Algorithms 33

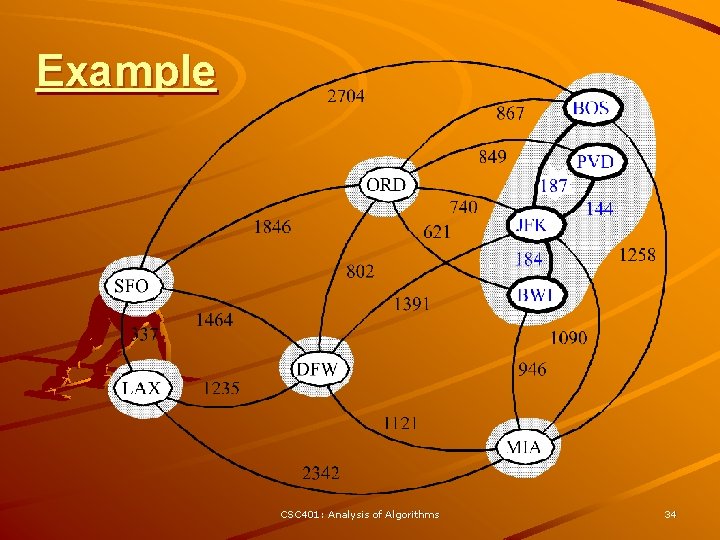
Example CSC 401: Analysis of Algorithms 34

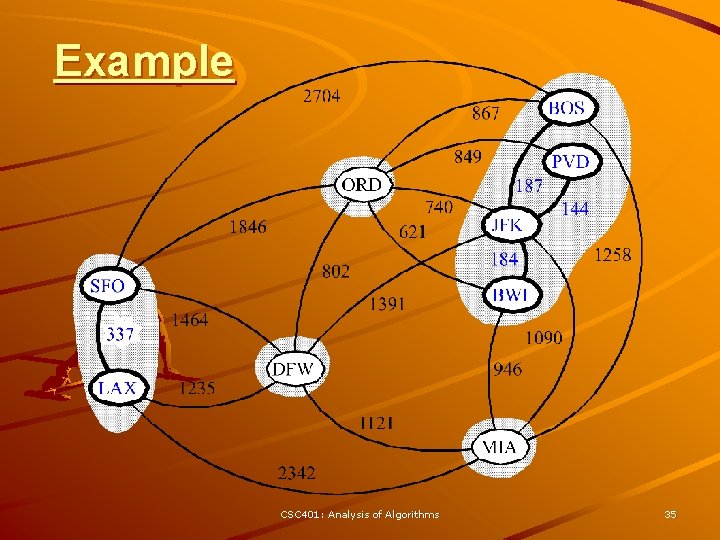
Example CSC 401: Analysis of Algorithms 35

Example CSC 401: Analysis of Algorithms 36

Example CSC 401: Analysis of Algorithms 37

Example CSC 401: Analysis of Algorithms 38

Example CSC 401: Analysis of Algorithms 39

Example CSC 401: Analysis of Algorithms 40

Example CSC 401: Analysis of Algorithms 41

Example CSC 401: Analysis of Algorithms 42

Example CSC 401: Analysis of Algorithms 43

Example 2704 BOS 867 849 ORD 740 621 1846 337 LAX 1391 1464 1235 187 144 JFK 1258 184 802 SFO PVD BWI 1090 DFW 946 1121 MIA 2342 CSC 401: Analysis of Algorithms 44

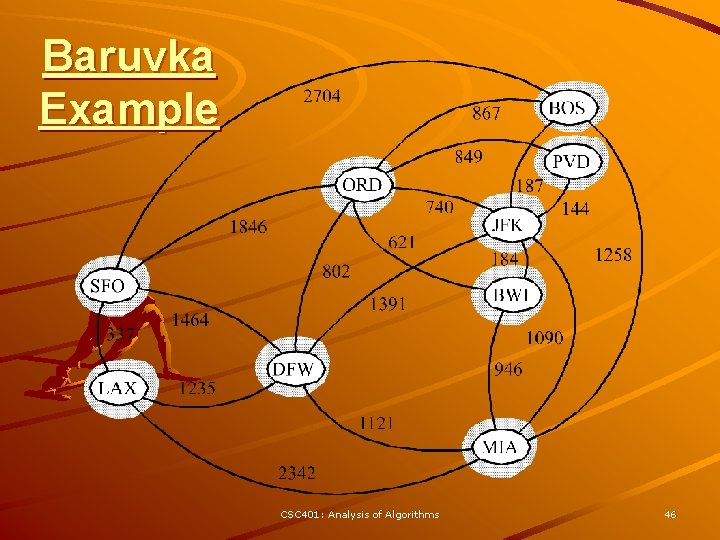
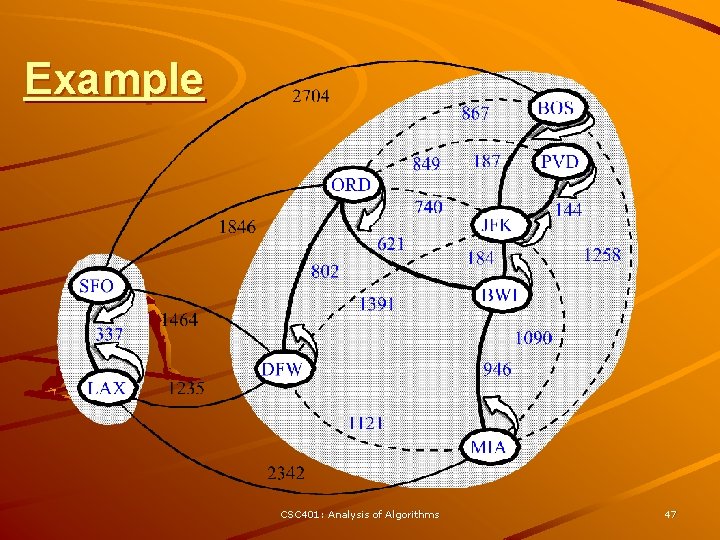
Baruvka’s Algorithm Like Kruskal’s Algorithm, Baruvka’s algorithm grows many “clouds” at once. Algorithm Baruvka. MST(G) T V {just the vertices of G} while T has fewer than n-1 edges do for each connected component C in T do Let edge e be the smallest-weight edge from C to another component in T. if e is not already in T then Add edge e to T return T Each iteration of the while-loop halves the number of connected compontents in T. – The running time is O(m log n). CSC 401: Analysis of Algorithms 45

Baruvka Example CSC 401: Analysis of Algorithms 46

Example CSC 401: Analysis of Algorithms 47

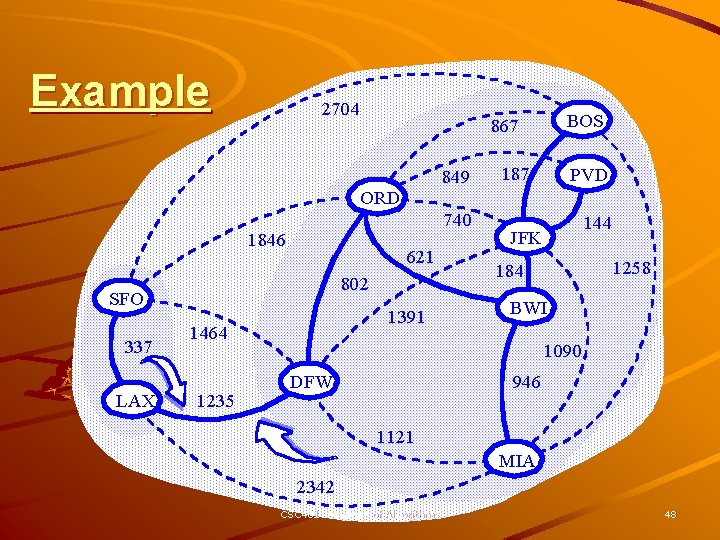
Example 2704 849 ORD 740 1846 621 802 SFO 337 LAX 1391 1464 1235 BOS 867 187 PVD 144 JFK 1258 184 BWI 1090 DFW 946 1121 MIA 2342 CSC 401: Analysis of Algorithms 48