CS 6501 2 D3 D Shape Manipulation 3

CS 6501 2 D/3 D Shape Manipulation, 3 D Printing Discrete Differential Geometry Surfaces Slides from Olga Sorkine, Eitan Grinspun

Surfaces, Parametric Form ● Continuous surface n pu pv p(u, v) ● Tangent plane at point p(u, v) is spanned by v u # 2

Isoparametric Lines ● Lines on the surface when keeping one parameter fixed v u # 3

Surface Normals ● Surface normal: n pu pv p(u, v) § Assuming regular parameterization, i. e. , v u # 4

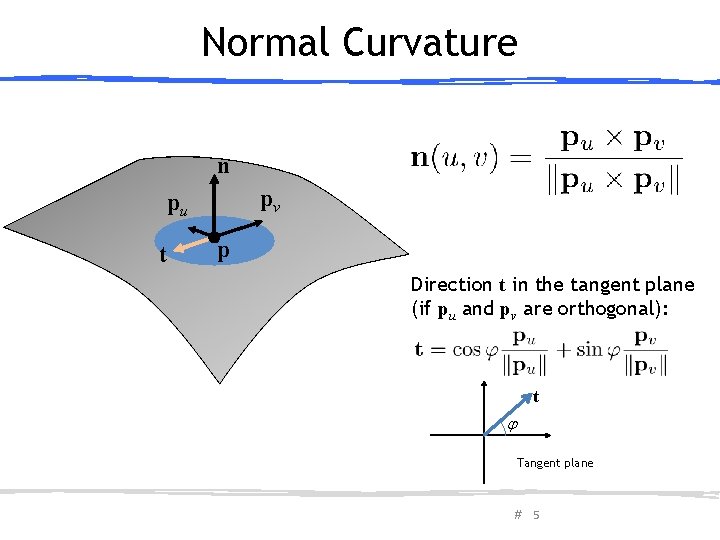
Normal Curvature n pv pu t p Direction t in the tangent plane (if pu and pv are orthogonal): t Tangent plane # 5

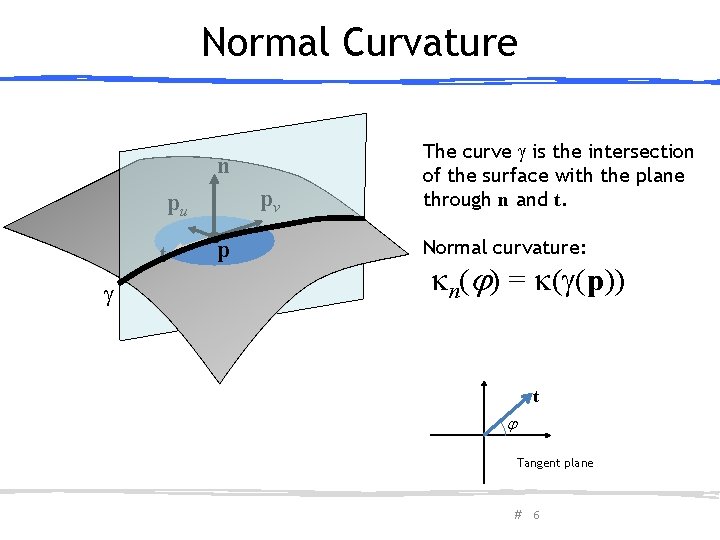
Normal Curvature n pv pu t p The curve is the intersection of the surface with the plane through n and t. Normal curvature: n( ) = ( (p)) t Tangent plane # 6

Surface Curvatures ● Principal curvatures § Maximal curvature § Minimal curvature ● Mean curvature ● Gaussian curvature # 7

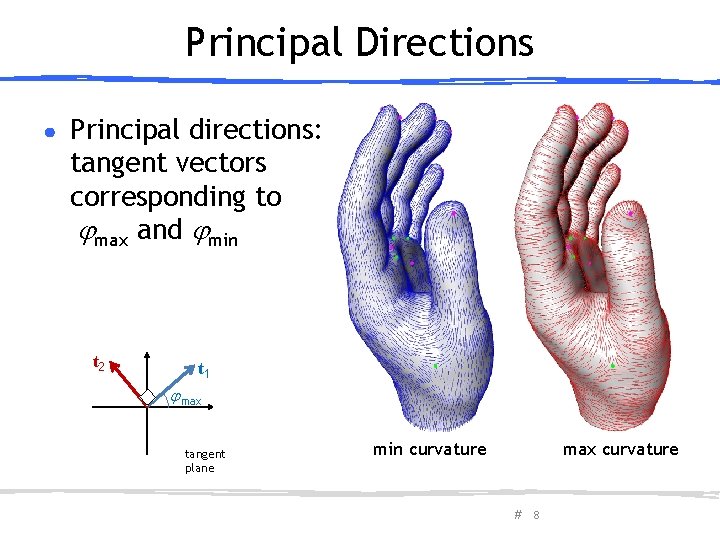
Principal Directions ● Principal directions: tangent vectors corresponding to max and min t 2 t 1 max tangent plane min curvature max curvature # 8

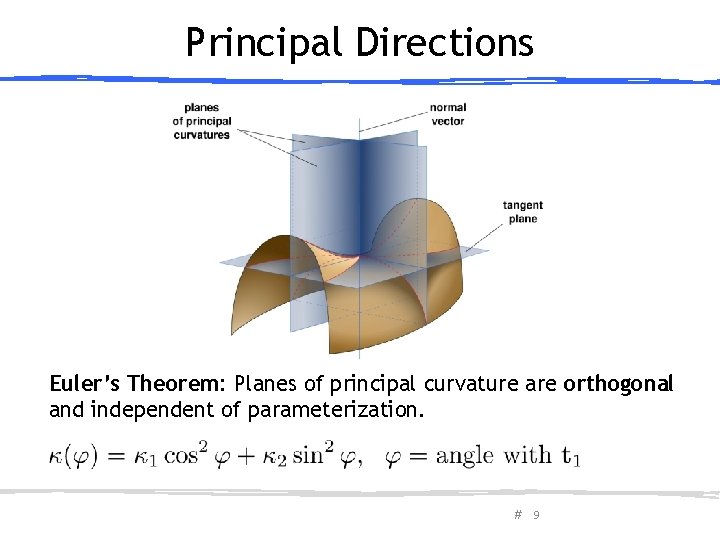
Principal Directions Euler’s Theorem: Planes of principal curvature are orthogonal and independent of parameterization. # 9

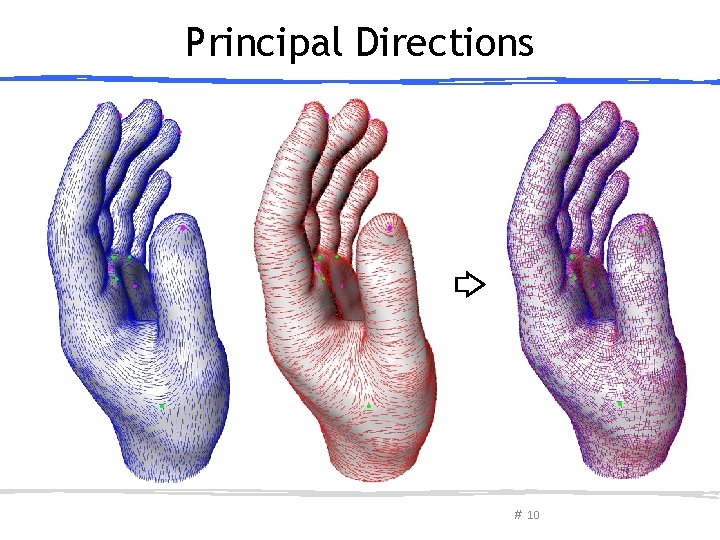
Principal Directions # 10

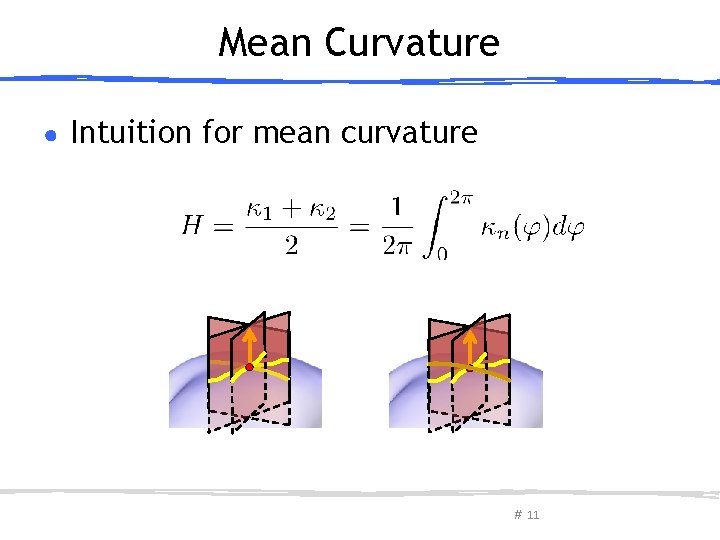
Mean Curvature ● Intuition for mean curvature # 11

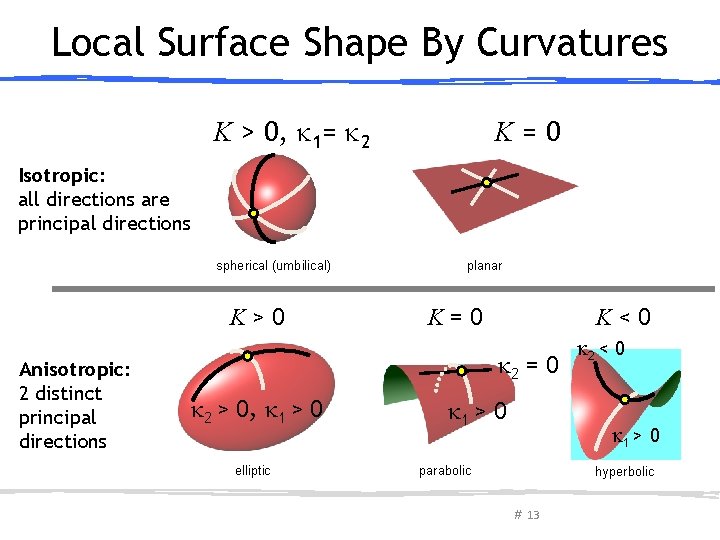
Classification ● A point p on the surface is called § § ● Elliptic, if K > 0 Parabolic, if K = 0 Hyperbolic, if K < 0 Umbilical, if Developable surface iff K = 0 # 12

Local Surface Shape By Curvatures K > 0, 1= 2 K=0 Isotropic: all directions are principal directions spherical (umbilical) K>0 Anisotropic: 2 distinct principal directions planar K=0 K<0 2 = 0 2 > 0, 1 > 0 elliptic 1 > 0 2 < 0 1 > 0 parabolic hyperbolic # 13

Gauss-Bonnet Theorem ● For a closed surface M: # 14

Gauss-Bonnet Theorem ● For a closed surface M: ● Compare with planar curves: # 15

Fundamental Forms ● First fundamental form ● Second fundamental form ● Together, they define a surface (given some compatibility conditions) # 16

Fundamental Forms ● I and II allow to measure § length, angles, area, curvature § arc element § area element # 17

Intrinsic Geometry ● Properties of the surface that only depend on the first fundamental form § length § angles § Gaussian curvature (Theorema Egregium) # 18

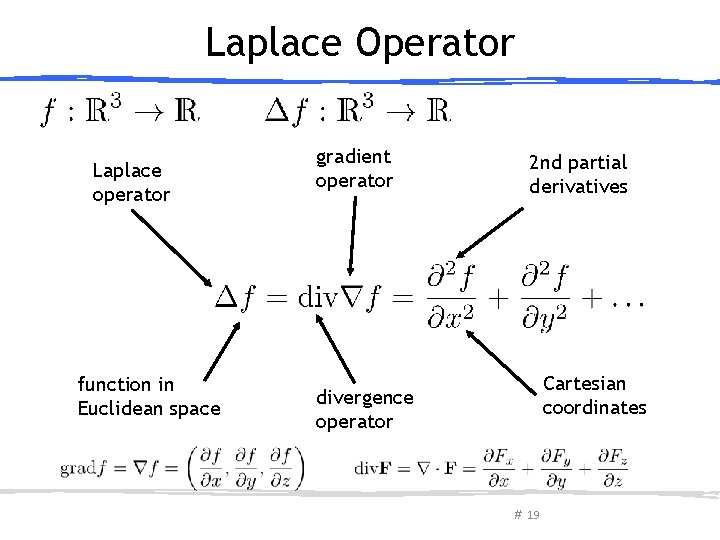
Laplace Operator Laplace operator function in Euclidean space gradient operator 2 nd partial derivatives Cartesian coordinates divergence operator # 19

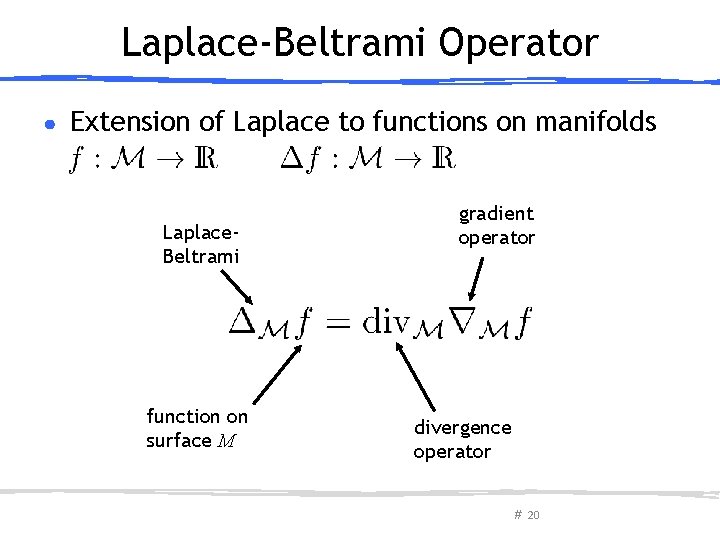
Laplace-Beltrami Operator ● Extension of Laplace to functions on manifolds Laplace. Beltrami function on surface M gradient operator divergence operator # 20

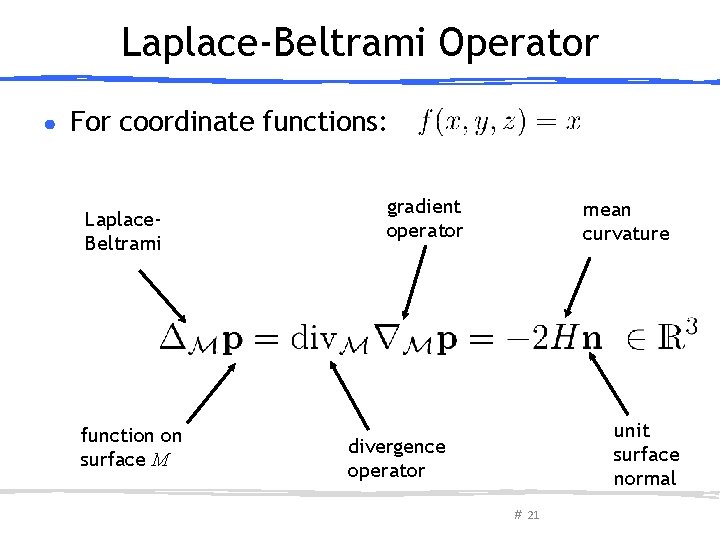
Laplace-Beltrami Operator ● For coordinate functions: Laplace. Beltrami function on surface M gradient operator mean curvature unit surface normal divergence operator # 21

Differential Geometry on Meshes ● Assumption: meshes are piecewise linear approximations of smooth surfaces Can try fitting a smooth surface locally (say, a polynomial) and find differential quantities analytically ● But: it is often too slow for interactive setting and error prone ● # 22

Discrete Differential Operators ● Approach: approximate differential properties at point v as spatial average over local mesh neighborhood N(v) where typically § v = mesh vertex § Nk(v) = k-ring neighborhood # 23

Discrete Laplace-Beltrami ● Uniform discretization: L(v) or ∆v ● Depends only on connectivity = simple and efficient ● Bad approximation for irregular triangulations vi vj # 24

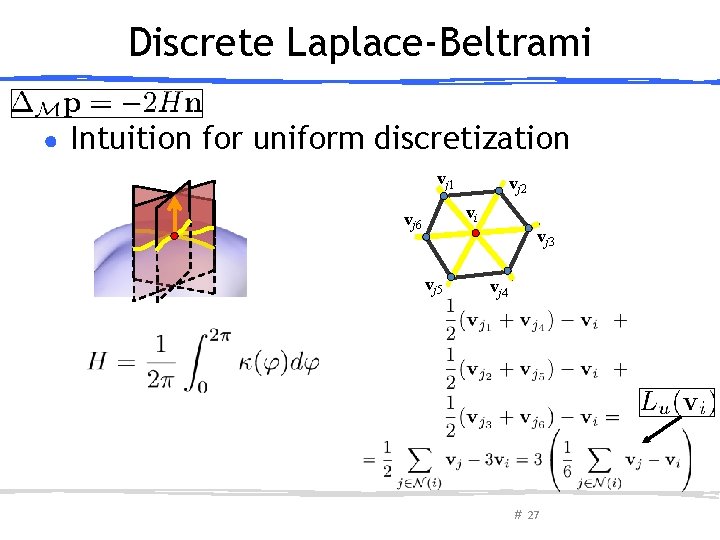
Discrete Laplace-Beltrami ● Intuition for uniform discretization # 25

Discrete Laplace-Beltrami ● Intuition for uniform discretization vi-1 v i+1 # 26

Discrete Laplace-Beltrami ● Intuition for uniform discretization vj 1 vj 2 vi vj 6 vj 3 vj 5 vj 4 # 27

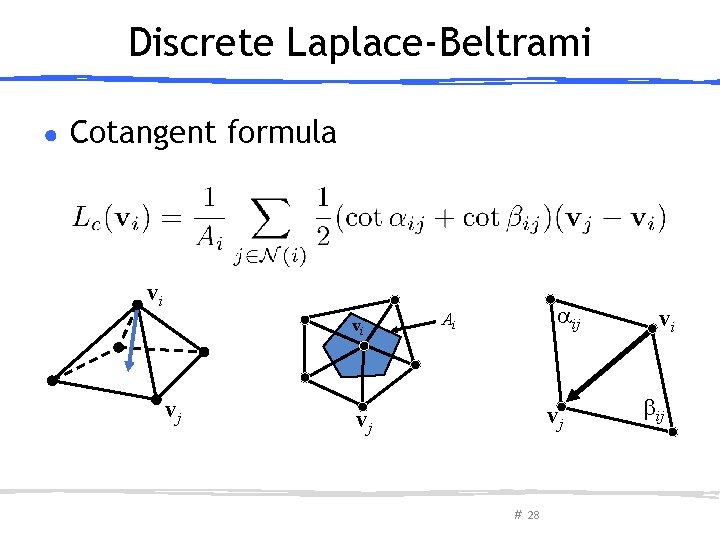
Discrete Laplace-Beltrami ● Cotangent formula vi vi vj ij Ai vj vj # 28 vi ij

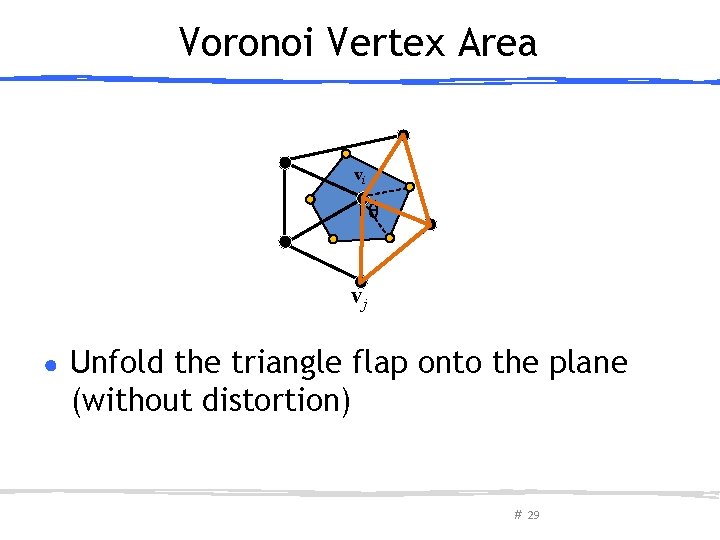
Voronoi Vertex Area vi θ vj ● Unfold the triangle flap onto the plane (without distortion) # 29

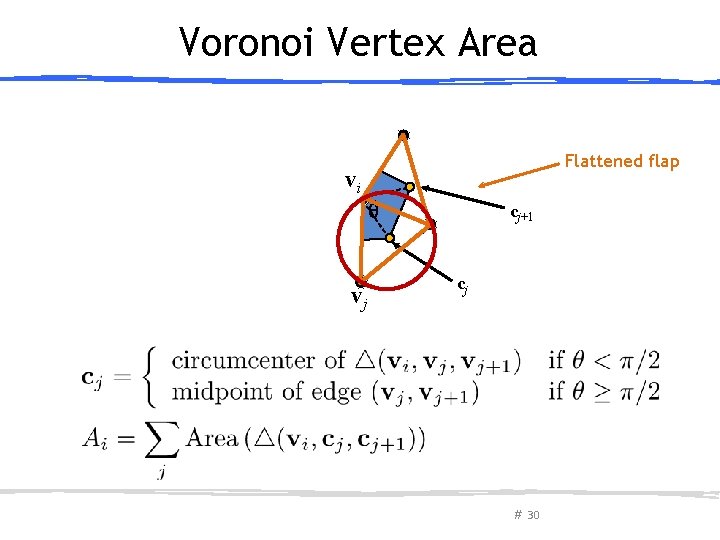
Voronoi Vertex Area Flattened flap vvi i θ vj cj+1 cj # 30

Discrete Laplace-Beltrami ● Cotangent formula § Accounts for mesh geometry § Potentially negative/ infinite weights # 31

Discrete Laplace-Beltrami ● Cotangent formula § Can be derived using linear Finite Elements § Nice property: gives zero for planar 1 -rings! # 32

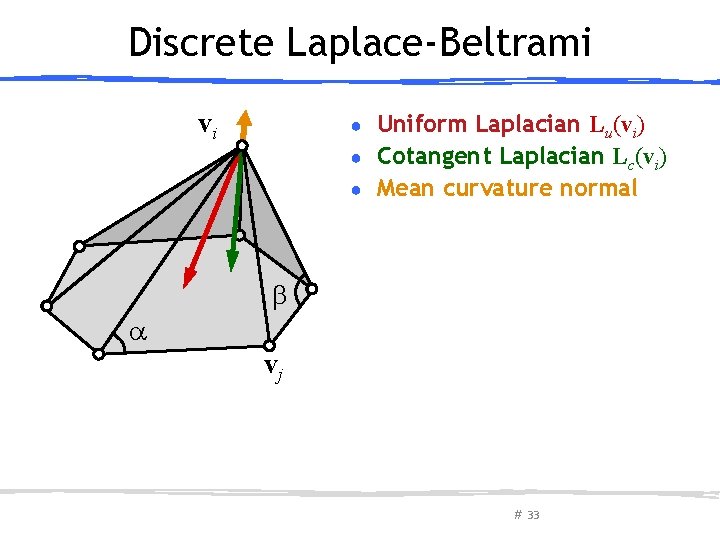
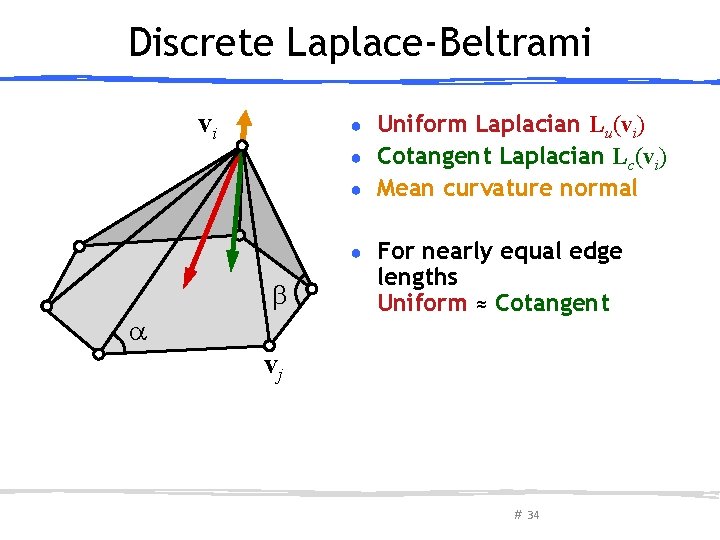
Discrete Laplace-Beltrami vi Uniform Laplacian Lu(vi) ● Cotangent Laplacian Lc(vi) ● Mean curvature normal ● vj # 33

Discrete Laplace-Beltrami vi Uniform Laplacian Lu(vi) ● Cotangent Laplacian Lc(vi) ● Mean curvature normal ● ● For nearly equal edge lengths Uniform ≈ Cotangent vj # 34

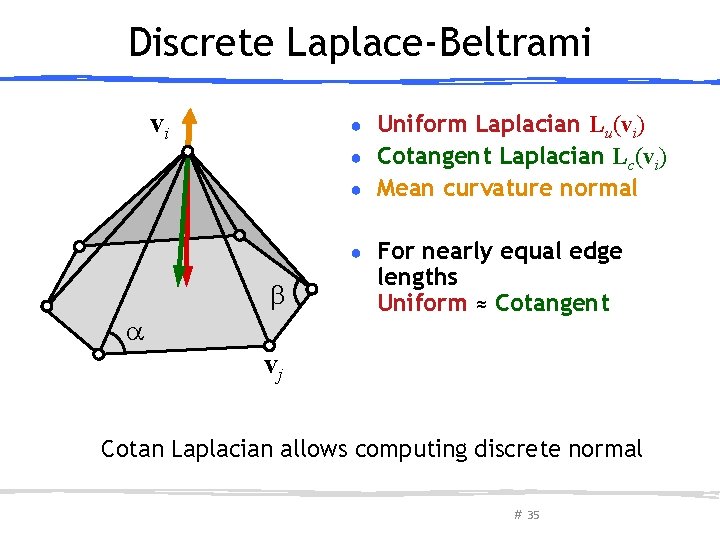
Discrete Laplace-Beltrami vi Uniform Laplacian Lu(vi) ● Cotangent Laplacian Lc(vi) ● Mean curvature normal ● ● For nearly equal edge lengths Uniform ≈ Cotangent vj Cotan Laplacian allows computing discrete normal # 35

Discrete Curvatures ● ● Mean curvature (sign defined according to normal) Ai Gaussian curvature j ● Principal curvatures # 36

Discrete Gauss-Bonnet Theorem ● Total Gaussian curvature is fixed for a given topology # 37

Example: Discrete Mean Curvature # 38

Links and Literature ● M. Meyer, M. Desbrun, P. Schroeder, A. Barr Discrete Differential-Geometry Operators for Triangulated 2 -Manifolds, Vis. Math, 2002 # 39

Links and Literature ● P. Alliez, Estimating Curvature Tensors on Triangle Meshes, Source Code ● http: //wwwsop. inria. fr/geometrica/team/Pierre. Alliez/demos/cu rvature/ principal directions # 40

Measuring Surface Smoothness # 41

Links and Literature ● Grinspun et al. : Computing discrete shape operators on general meshes, Eurographics 2006 # 42

Reflection Lines as an Inspection Tool ● Shape optimization using reflection lines E. Tosun, Y. I. Gingold, J. Reisman, D. Zorin Symposium on Geometry Processing 2007 # 43

Reflection Lines as an Inspection Tool ● Shape optimization using reflection lines E. Tosun, Y. I. Gingold, J. Reisman, D. Zorin Symposium on Geometry Processing 2007 # 44

Thank You