CS 6501 2 D3 D Shape Manipulation 3






























- Slides: 49

CS 6501 2 D/3 D Shape Manipulation, 3 D Printing Digital Geometry Processing -Mesh Smoothing March 27, 2013

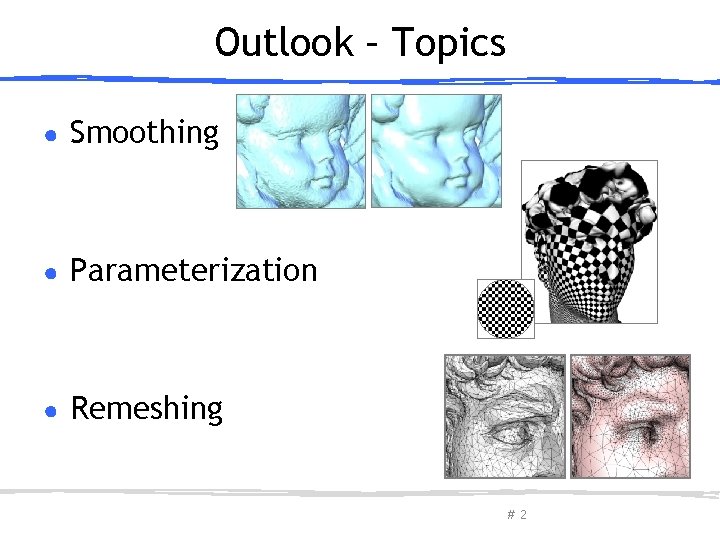
Outlook – Topics ● Smoothing ● Parameterization ● Remeshing March 27, 2013 Olga Sorkine-Hornung # 2

Surface Smoothing – Motivation ● Scanned surfaces can be noisy March 27, 2013 Olga Sorkine-Hornung # 3

Surface Smoothing – Motivation ● Scanned surfaces can be noisy March 27, 2013 Olga Sorkine-Hornung # 4

Surface Fairing – Motivation ● Marching Cubes meshes can be ugly • Why is the left mesh ugly? • Why is the right mesh ugly? § What is the problem with such triangles? March 27, 2013 Olga Sorkine-Hornung # 5

Filtering Curves ● Discrete second derivative: ● In matrix-vector form for the whole curve March 27, 2013 Olga Sorkine-Hornung # 6

Filtering Curves ● Gaussian filtering Scale factor 0 < < 1 ● Matrix-vector form: ● March 27, 2013 Olga Sorkine-Hornung # 7

Filtering Curves ● Gaussian filtering ● Scale factor 0 < < 1 ● Drawbacks § ? March 27, 2013 Olga Sorkine-Hornung # 8

Filtering Curves ● Gaussian filtering ● Scale factor 0 < < 1 ● Drawbacks § Causes the curve/mesh to shrink; slow March 27, 2013 Olga Sorkine-Hornung # 9

Filtering Curves Original curve March 27, 2013 Olga Sorkine-Hornung # 10

Filtering Curves 1 st iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 11

Filtering Curves 2 nd iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 12

Filtering Curves 8 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 13

Filtering Curves 27 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 14

Filtering Curves 50 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 15

Filtering Curves 500 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 16

Filtering Curves 1000 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 17

Filtering Curves 5000 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 18

Filtering Curves 10000 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 19

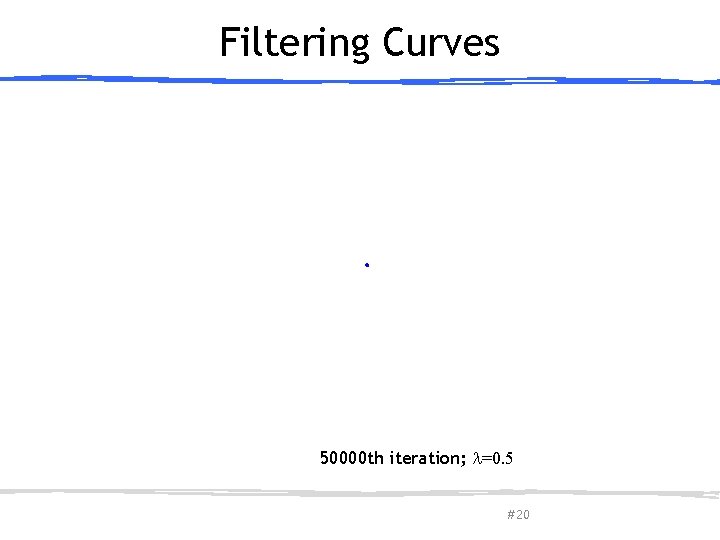
Filtering Curves 50000 th iteration; =0. 5 March 27, 2013 Olga Sorkine-Hornung # 20

Recap: Laplace-Beltrami High-pass filter: extracts local surface detail ● Detail = smooth(surface) – surface ● Smoothing = averaging ● March 27, 2013 Olga Sorkine-Hornung # 21

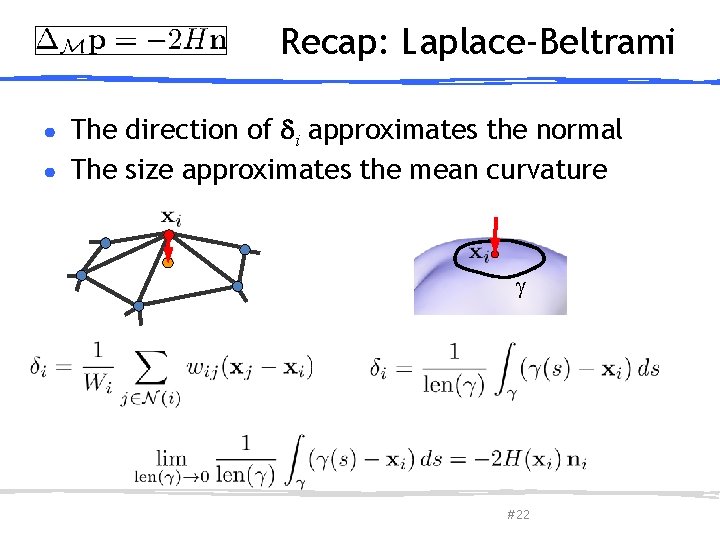
Recap: Laplace-Beltrami The direction of i approximates the normal ● The size approximates the mean curvature ● March 27, 2013 Olga Sorkine-Hornung # 22

L-B: Weighting Schemes ● Ignore geometry uniform : Wi = 1, wij = 1/di ● Integrate over Voronoi region of the vertex n cotan : wij = 0. 5(cot aij + cot bij) aij Wi =Ai March 27, 2013 Olga Sorkine-Hornung # 23 bij

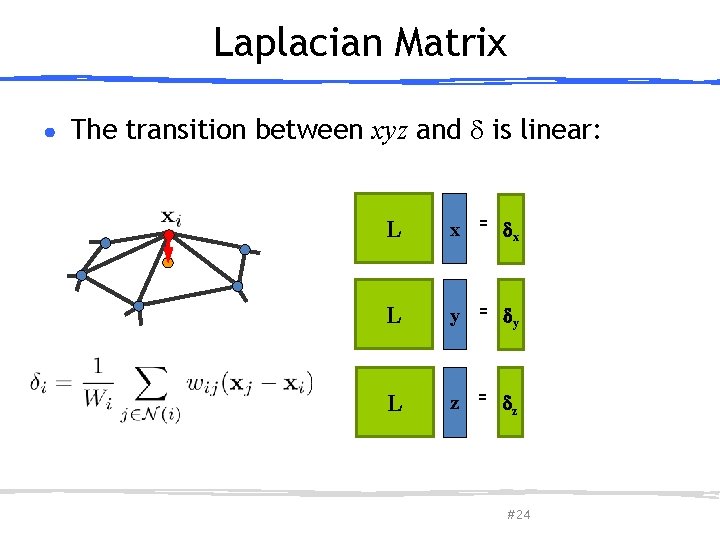
Laplacian Matrix ● The transition between xyz and is linear: March 27, 2013 L x = x L y = y L z = z Olga Sorkine-Hornung # 24

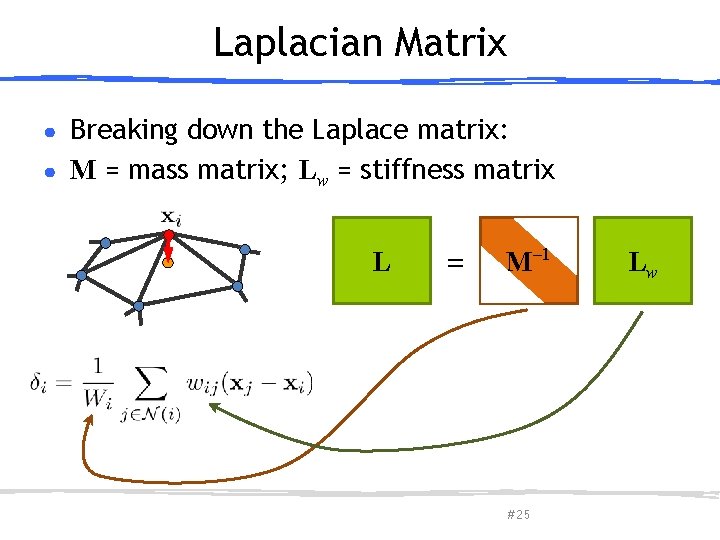
Laplacian Matrix Breaking down the Laplace matrix: ● M = mass matrix; Lw = stiffness matrix ● L March 27, 2013 Olga Sorkine-Hornung = M– 1 # 25 Lw

Taubin Smoothing: Explicit Steps ● Iterate: ● > 0 to smooth; < 0 to inflate ● Originally proposed with uniform Laplacian weights original 10 iterations 50 iterations 200 iterations A Signal Processing Approach to Fair Surface Design Gabriel Taubin ACM SIGGRAPH 95 March 27, 2013 Olga Sorkine-Hornung # 26

Taubin Smoothing: Explicit Steps ● ● Per-vertex iterations Simple to implement Requires many iterations ● Need to tweak μ and λ original 10 iterations 50 iterations 200 iterations ● A Signal Processing Approach to Fair Surface Design Gabriel Taubin ACM SIGGRAPH 95 March 27, 2013 Olga Sorkine-Hornung # 27

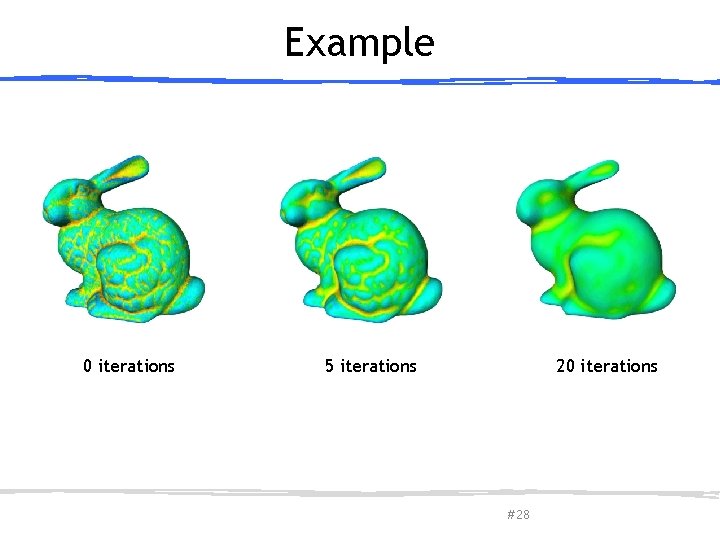
Example 0 iterations March 27, 2013 20 iterations 5 iterations Olga Sorkine-Hornung # 28

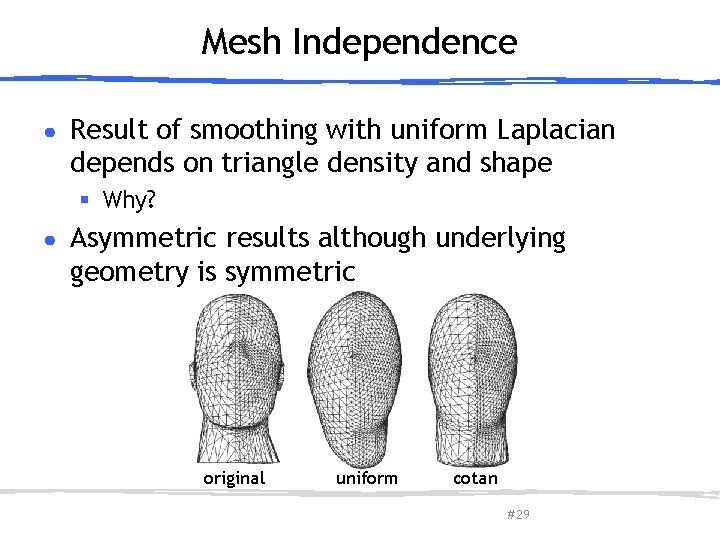
Mesh Independence ● Result of smoothing with uniform Laplacian depends on triangle density and shape § Why? ● Asymmetric results although underlying geometry is symmetric original March 27, 2013 uniform Olga Sorkine-Hornung cotan # 29

Mesh Independence ● Result of smoothing with uniform Laplacian depends on triangle density and shape § Why? ● Asymmetric results although underlying geometry is symmetric original March 27, 2013 uniform Olga Sorkine-Hornung cotan # 30

Implicit Fairing: Implicit Euler Steps ● In each iteration, solve for the smoothed x : Implicit fairing of irregular meshes using diffusion and curvature flow M. Desbrun, M. Meyer, P. Schroeder, A. Barr ACM SIGGRAPH 99 March 27, 2013 Olga Sorkine-Hornung # 31

Smoothing as (mean curvature) Flow ● Model smoothing as a diffusion process ● Discretize in time, forward differences: March 27, 2013 Olga Sorkine-Hornung # 32

Smoothing as (mean curvature) Flow ● Model smoothing as a diffusion process ● Discretize in time, forward differences: Explicit integration Unstable unless time step dt is small March 27, 2013 Olga Sorkine-Hornung # 33

Smoothing as (mean curvature) Flow ● Model smoothing as a diffusion process ● Backward Euler for unconditional stability March 27, 2013 Olga Sorkine-Hornung # 34

Implicit Fairing Implicit fairing of irregular meshes using diffusion and curvature flow M. Desbrun, M. Meyer, P. Schroeder, A. Barr ACM SIGGRAPH 99 March 27, 2013 Olga Sorkine-Hornung # 35

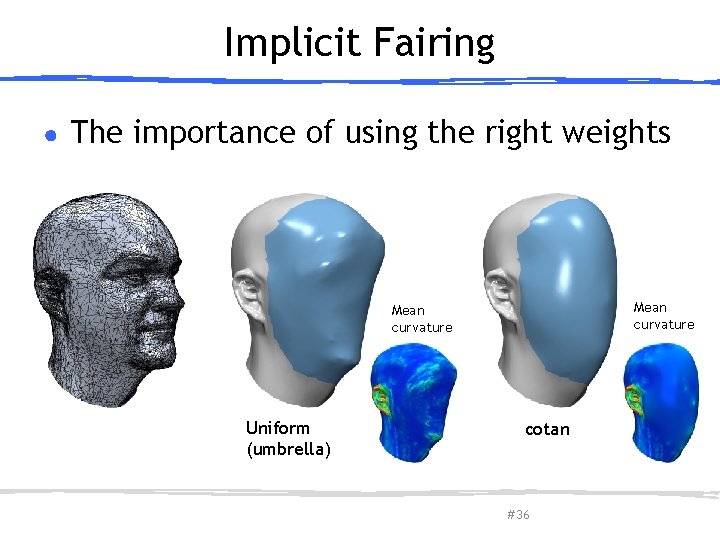
Implicit Fairing ● The importance of using the right weights Mean curvature Uniform (umbrella) March 27, 2013 Olga Sorkine-Hornung cotan # 36

Laplacian Mesh Optimization Smoothing, improving of triangle shapes ● Basic idea: formulate a “shopping list”, solve with least squares ● Laplacian Mesh Optimization ACM GRAPHITE 2006 A. Nealen, T. Igarashi, O. Sorkine, M. Alexa March 27, 2013 Olga Sorkine-Hornung # 37

Laplacian Mesh Optimization Smoothing, improving of triangle shapes ● Basic idea: formulate a “shopping list”, solve with least squares ● § § Smooth mesh: Lx = 0 Passes close to input data set: x = x Well-shaped triangles: Luni x = Lcot x The terms are weighted according to importance and geometry Laplacian Mesh Optimization ACM GRAPHITE 2006 A. Nealen, T. Igarashi, O. Sorkine, M. Alexa March 27, 2013 Olga Sorkine-Hornung # 38

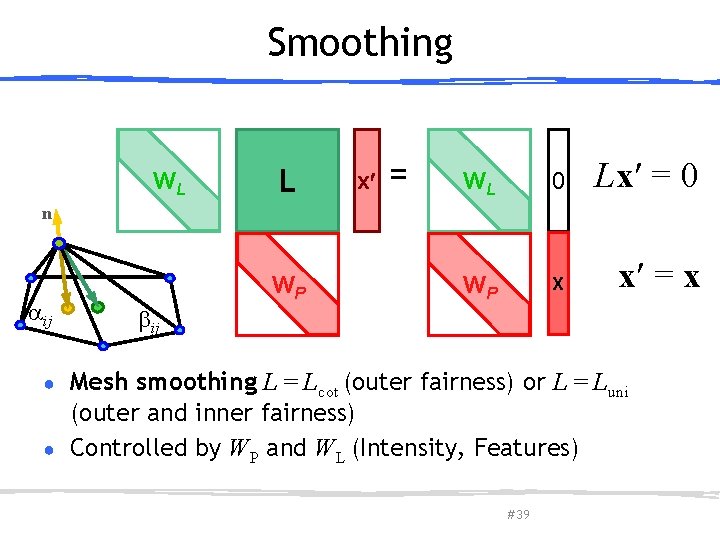
Smoothing WL L x = WL 0 Lx = 0 WP X x = x n aij WP bij Mesh smoothing L = Lcot (outer fairness) or L = Luni (outer and inner fairness) ● Controlled by WP and WL (Intensity, Features) ● March 27, 2013 Olga Sorkine-Hornung # 39

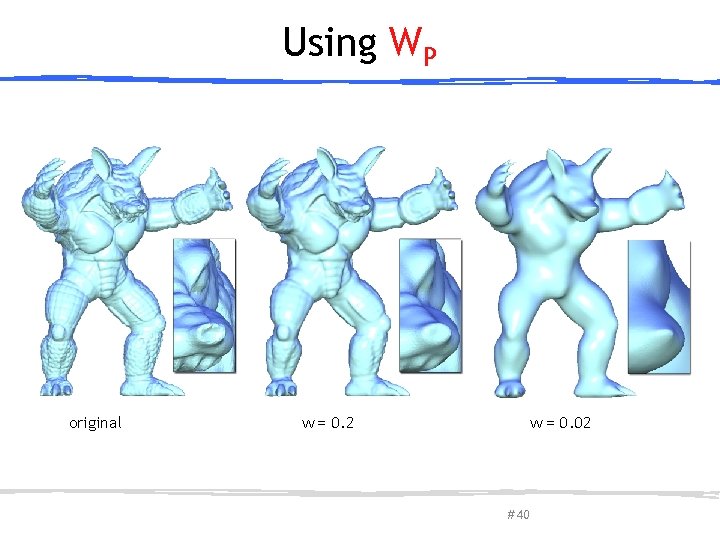
Using WP original w = 0. 2 March 27, 2013 Olga Sorkine-Hornung w = 0. 02 # 40

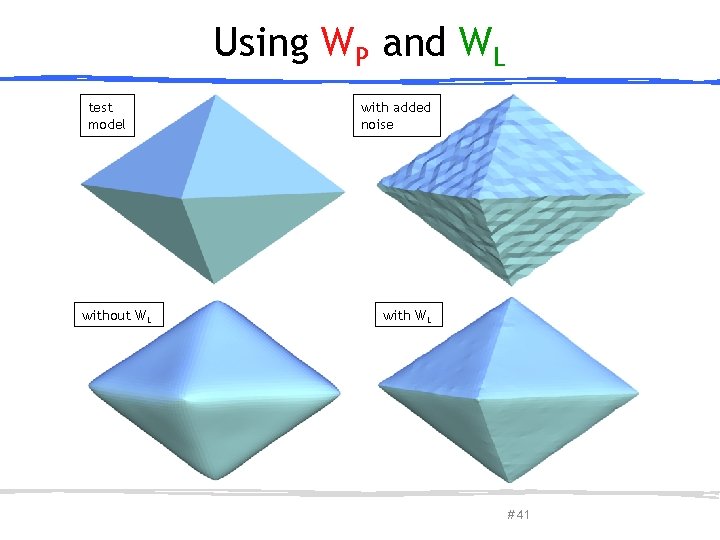
Using WP and WL test model with added noise without WL March 27, 2013 with WL Olga Sorkine-Hornung # 41

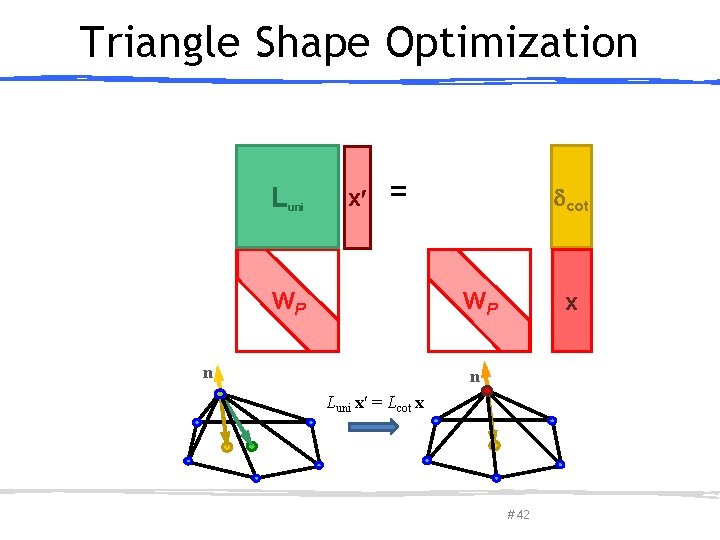
Triangle Shape Optimization L uni x = WP cot WP n x n Luni x = Lcot x March 27, 2013 Olga Sorkine-Hornung # 42

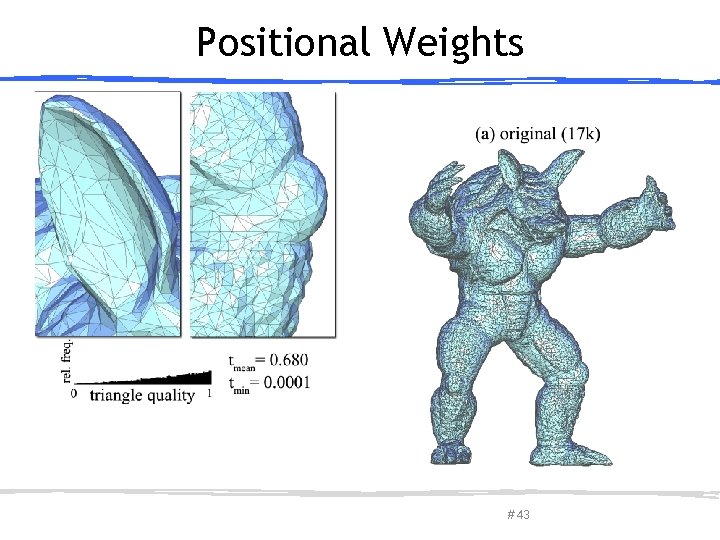
Positional Weights March 27, 2013 Olga Sorkine-Hornung # 43

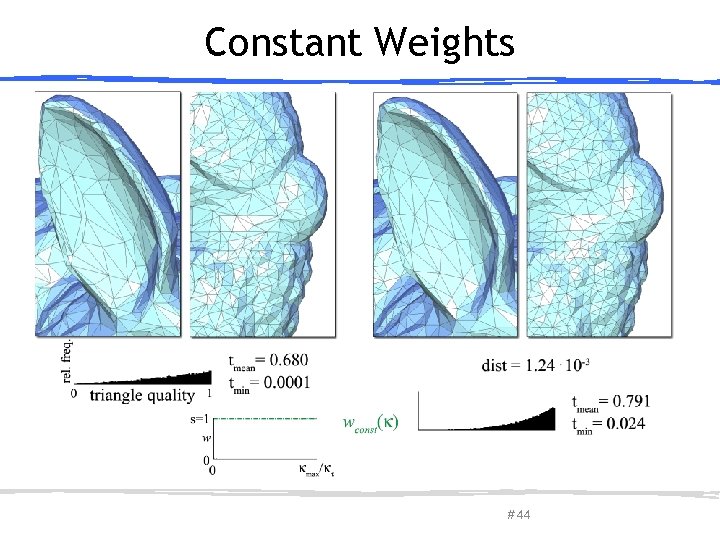
Constant Weights March 27, 2013 Olga Sorkine-Hornung # 44

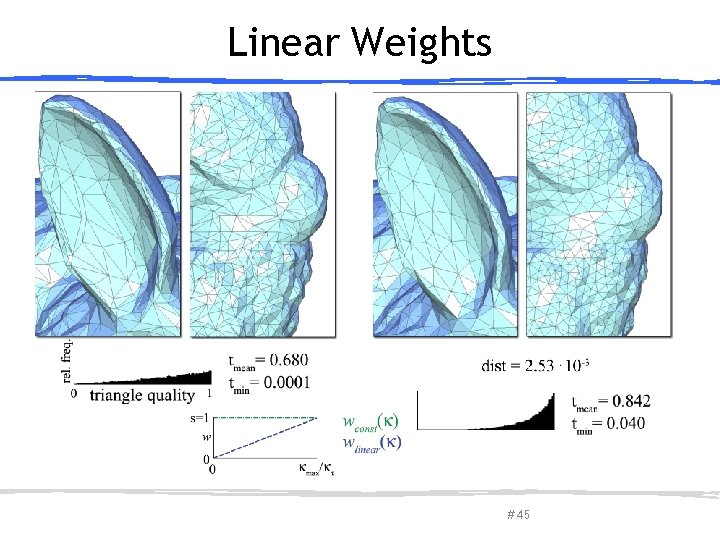
Linear Weights March 27, 2013 Olga Sorkine-Hornung # 45

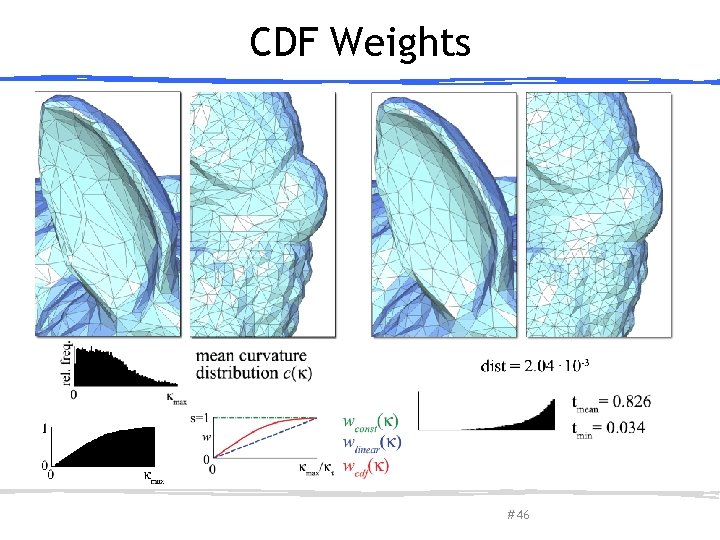
CDF Weights March 27, 2013 Olga Sorkine-Hornung # 46

Original March 27, 2013 Olga Sorkine-Hornung # 47

Triangle Shape Optimization March 27, 2013 Olga Sorkine-Hornung # 48

Thank You March 27, 2013