CPT and Lorentz Invariance and Violation in QFT

CPT and Lorentz Invariance and Violation in QFT Yue-Liang Wu Kavli Institute for Theoretical Physics China Key Laboratory of Frontiers in Theoretical Physics Institute of Theoretical Physics, CAS Chinese Academy of Sciences

Symmetry & Quantum Field Theory n n Symmetry has played an important role in physics CPT and Lorentz invariance are regarded as the fundamental symmetries of nature. CPT invariance is the basic property of relativistic quantum field theory for point particle. All known basic forces of nature: electromagnetic, weak, strong & gravitational forces, are governed by the local gauge symmetries: U(1)_Y x SU(2)_L x SU(3)_c x SO(1, 3)

Lorentz and CPT Violation in QFT n n n QFT may not be an underlying theory but EFT In String Theory, Lorentz invariance can be broken down spontaneously. Lorentz non-invariant quantum field theory Explicit、Spontaneous 、Induced CPT/Lorentz violating Chern-Simons term constant vector

Induced CTP/Lorentz Violation n n Real world has been found to be successfully described by quantum field theories EQED with constant vector mass n What is the relation ?

Diverse Results n Gauge invariance of axial-current S. Coleman and S. L. Glashow, Phys. Rev. D 59: 116008 (1999) n Pauli-Villas regularization with D. Colladay and V. A. Kostelecky, Phys. Rev. D 58: 116002 (1998). n Gauge invariance and conservation of vector Ward identity M. Perez-Victoria, JHEP 0104 032 (2001). n Consistent analysis via dimensional regularization G. Bonneau, Nucl. Phys. B 593 398 (2001).

Diverse Results n Based on nonperturbative formulation with R. Jackiw and V. A. Kostelecky, Phys. Rev. Lett. 82: 3572 (1999). n Derivative Expansion with dimensional regularization J. M. Chung and P. Oh, Phys. Rev. D 60: 067702 (1999). n Keep full dependence with M. Perez-Victoria, Phys. Rev. Lett. 83: 2518 (1999).

Consistent Result n n Statement in Literature: constant vector K can only be determined by experiment Our Conclusion: constant vector K can consistently be fixed from theoretical calculations n for

Regularization Scheme Regularization scheme dependence n n n Ambiguity of Dimensional regularization with problem Ambiguity with momentum translation for linear divergent term Ambiguity of reducing triangle diagrams How to reach a consistent regularization scheme ?

Regularization Methods n n n Cut-off regularization Keeping divergent behavior, spoiling gauge symmetry & translational/rotational symmetries Pauli-Villars regularization Modifying propagators, destroying non-abelian gauge symmetry, introduction of superheavy particles Dimensional regularization: analytic continuation in dimension Gauge invariance, widely used for practical calculations Gamma_5 problem, losing scaling behavior (incorrect gap eq. ), problem to chiral theory and super-symmetric theory All the regularizations have their advantages and shortcomings

Criteria of Consistent Regularization (i) The regularization is rigorous that it can maintain the basic symmetry principles in the original theory, such as: gauge invariance, Lorentz invariance and translational invariance (ii) The regularization is general that it can be applied to both underlying renormalizable QFTs (such as QCD) and effective QFTs (like the gauged Nambu-Jona. Lasinio model and chiral perturbation theory).

Criteria of Consistent Regularization (iii) The regularization is also essential in the sense that it can lead to the well-defined Feynman diagrams with maintaining the initial divergent behavior of integrals. so that the regularized theory only needs to make an infinity-free renormalization. (iv) The regularization must be simple that it can provide the practical calculations.

Symmetry-Preserving Loop Regularization (LORE) with String Mode Regulators n Yue-Liang Wu, SYMMETRY PRINCIPLE PRESERVING AND INFINITY FREE REGULARIZATION AND RENORMALIZATION OF QUANTUM FIELD THEORIES AND THE MASS GAP. Int. J. Mod. Phys. A 18: 2003, 5363 -5420. n Yue-Liang Wu, SYMMETRY PRESERVING LOOP REGULARIZATION AND RENORMALIZATION OF QFTS. Mod. Phys. Lett. A 19: 2004, 2191 -2204.

Why Quantum Field Theory So Successful n Folk’s theorem by Weinberg: Any quantum theory that at sufficiently low energy and large distances looks Lorentz invariant and satisfies the cluster decomposition principle will also at sufficiently low energy look like a quantum field theory. n n Indication: existence in any case a characterizing energy scale (CES) M_c At sufficiently low energy then means: E << M_c QFTs

Why Quantum Field Theory So Successful n Renormalization group by Wilson or Gell-Mann & Low Allow to deal with physical phenomena at any interesting energy scale by integrating out the physics at higher energy scales. To be able to define the renormalized theory at any interesting renormalization scale. n Implication: Existence of sliding energy scale (SES) μ_s which is not related to masses of particles. n The physical effects above the SES μ_s are integrated in the renormalized couplings and fields.

Irreducible Loop Integrals (ILIs)

Loop Regularization (LORE) Simple Prescription: in ILIs, make the following replacement With the conditions So that

Gauge Invariant Consistency Conditions

Checking Consistency Condition

Checking Consistency Condition

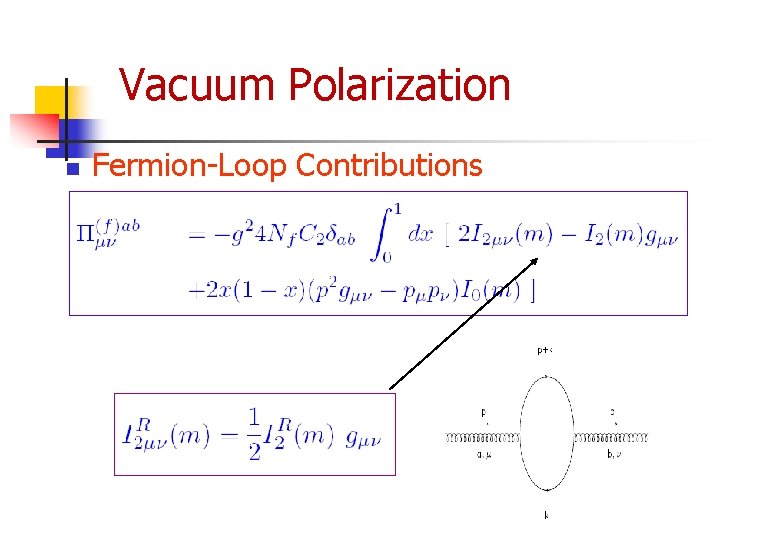
Vacuum Polarization n Fermion-Loop Contributions

Gluonic Loop Contributions

Cut-Off & Dimensional Regularizations n Cut-off violates consistency conditions n DR satisfies consistency conditions n But quadratic behavior is suppressed in DR

Symmetry–preserving & Infinity-free Loop Regularization (LORE) With String-mode Regulators n Choosing the regulator masses to have the string -mode Reggie trajectory behavior n Coefficients are completely determined n from the conditions

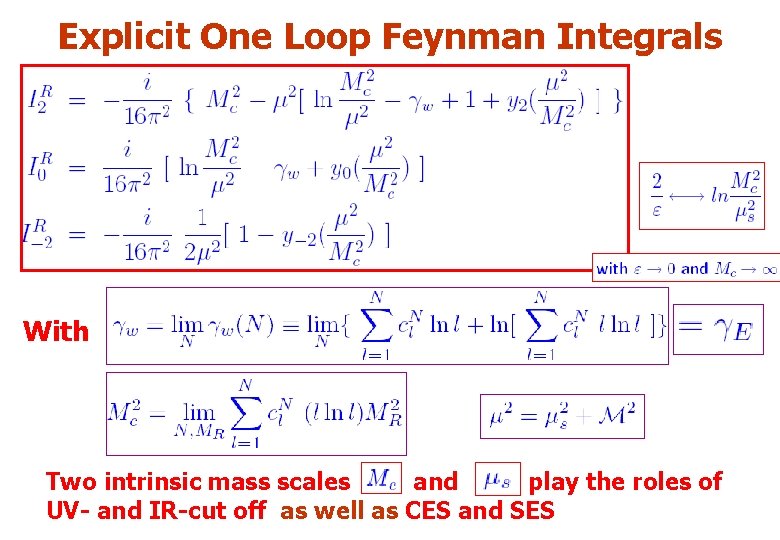
Explicit One Loop Feynman Integrals With Two intrinsic mass scales and play the roles of UV- and IR-cut off as well as CES and SES

Interesting Mathematical Identities which lead the functions to the following simple forms

Renormalization Constants of Non- Abelian gauge Theory and β Function of QCD in Loop Regularization Jian-Wei Cui, Yue-Liang Wu, Int. J. Mod. Phys. A 23: 2861 -2913, 2008 n Lagrangian of gauge theory n Possible counter-terms

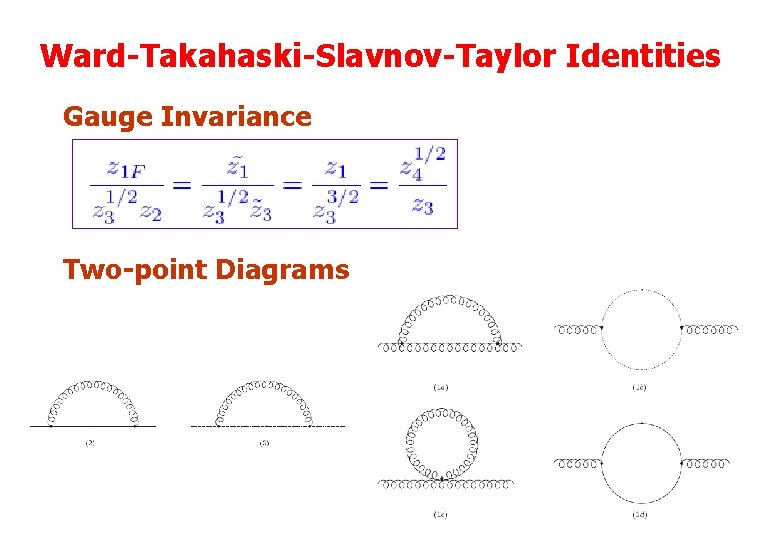
Ward-Takahaski-Slavnov-Taylor Identities Gauge Invariance Two-point Diagrams

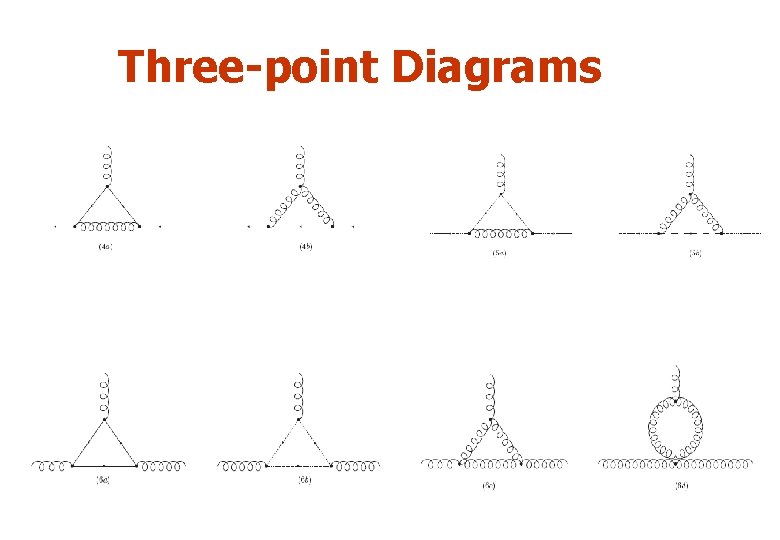
Three-point Diagrams

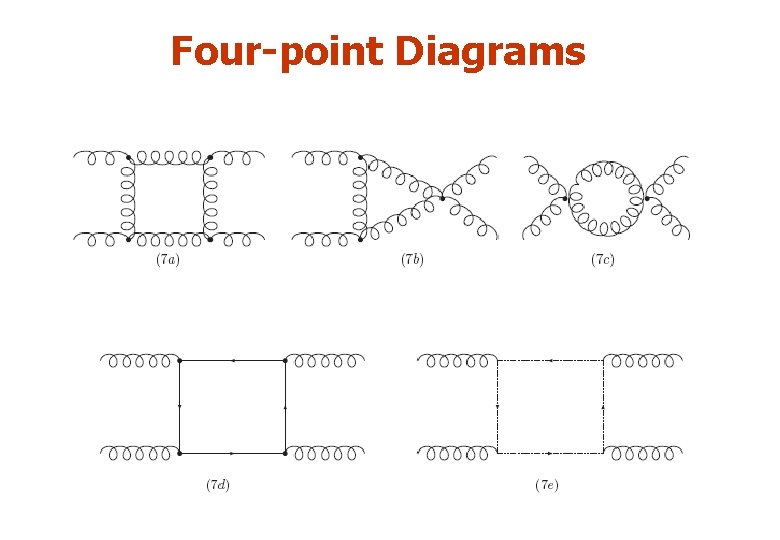
Four-point Diagrams

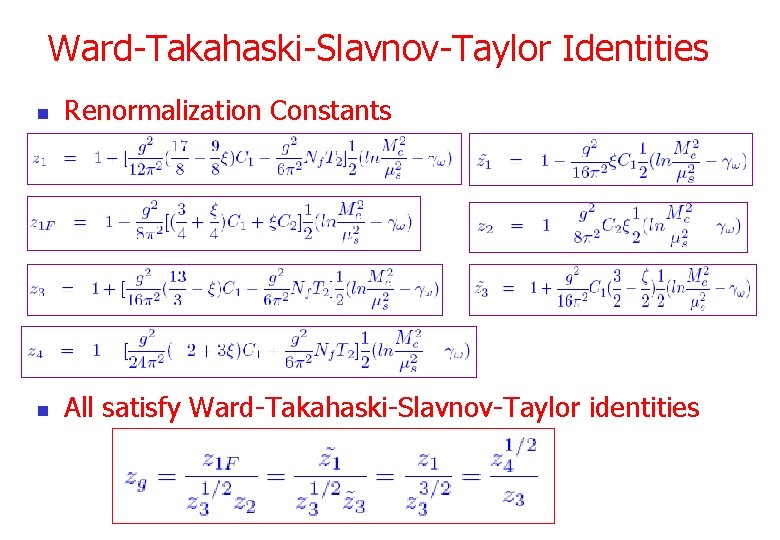
Ward-Takahaski-Slavnov-Taylor Identities n Renormalization Constants n All satisfy Ward-Takahaski-Slavnov-Taylor identities

Renormalization β Function n Gauge Coupling Renormalization which reproduces the well-known QCD β function (GWP)

Supersymmetry in Loop Regularization J. W. Cui, Y. Tang, Y. L. Wu Phys. Rev. D 79: 125008, 2009 Supersymmetry n n n Supersymmetry is a full symmetry of quantum theory Supersymmetry should be Regularizationindependent Supersymmetry-preserving regularization

Massless Wess-Zumino Model n Lagrangian n Ward identity n In momentum space

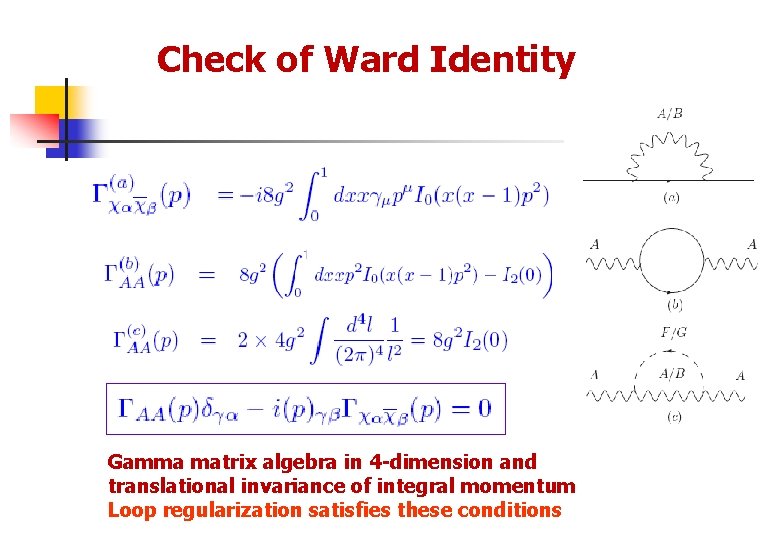
Check of Ward Identity Gamma matrix algebra in 4 -dimension and translational invariance of integral momentum Loop regularization satisfies these conditions

Massive Wess-Zumino Model n Lagrangian n Ward identity

Check of Ward Identity Gamma matrix algebra in 4 -dimension and translational invariance of integral momentum Loop regularization satisfies these conditions

Triangle Anomaly n Amplitudes n Using the definition of gamma_5 n The trace of gamma matrices gets the most general and unique structure with symmetric Lorentz indices

Anomaly of Axial Current n n Explicit calculation based on Loop Regularization with the most general and symmetric Lorentz structure Restore the original theory in the limit which shows that vector currents are automatically conserved, only the axial-vector Ward identity is violated by quantum corrections

Chiral Anomaly Based on Loop Regularization Including the cross diagram, the final result is Which leads to the well-known anomaly form

Anomaly Based on Various Regularizations n n Using the most general and symmetric trace formula for gamma matrices with gamma_5. In unit

Quantum Loop Induced CPT/Lorentz Violating Chern-Simons Term in Loop Regularization n Amplitudes of triangle diagrams

Contributions to Amplitudes n Convergent contributions n Divergent contributions n Logarithmic DV Linear DV

Contributions to Amplitudes n Logarithmic Divergent Contributions n Regularized result with LORE

Contributions to Amplitudes n Linear divergent contributions n Regularized result

Contributions to Amplitudes n Total contributions arise from convergent part

Final Result n Setting n Final result is

Comments on Ambiguity n n Momentum translation relation of linear divergent Regularization after using the relation

Check on Consistency n Ambiguity of results n Inconsistency with U(1) chiral anomaly of

Conclusions n n First applying for the regularization before using momentum translation relation of linear divergent integral Loop regularization is translational invariant Induced Chern-Simons term is uniqely determined when combining the chiral anomaly There is no harmful induced Chern-Simons term for massive fermions.

THANKS