LHC ILC Cosmology Interplay Sabine Kraml CERN WHEPP9

LHC / ILC / Cosmology Interplay Sabine Kraml (CERN) WHEPP-9, Bhubaneswar, India 3 -14 Jan 2006 S. Kraml WHEPP-9 Bhubaneswar

Outline Introduction n Relic density of WIMPs n SUSY case as illustrative example n Neutralino dark matter ¨ Requirements for collider tests ¨ Implications of CP violation ¨ n Conclusions S. Kraml WHEPP-9 Bhubaneswar 2

What is the Universe made of? n Cosmological data: ¨ 4% ± 0. 4% baryonic matter ¨ 23% ± 4% dark matter ¨ 73% ± 4% dark energy n Particle physics: ¨ SM is incomplete; expect new physics at Te. V scale ¨ NP should provide the DM ¨ Discovery at LHC, precision measurements at ILC ? S. Kraml WHEPP-9 Bhubaneswar 3

Dark matter candidates Neutralino, gravitino, axion, axino, lightest KK particle, T-odd little Higgs, branons, Q-balls, etc. . . New Physics S. Kraml WHEPP-9 Bhubaneswar 4

WIMPs (weakly interacting massive particles) n DM must be stable, electrically neutral, weakly and gravitationally interacting n WIMPs are predicted by most BSM theories n Stable as result of discrete symmetries n Produced as thermal relic of the Big Bang n Testable at colliders! S. Kraml WHEPP-9 Bhubaneswar Neutralino, gravitino, axion, axino, LKP, T-odd Little Higgs, branons, Q-balls, etc. , . . . 5

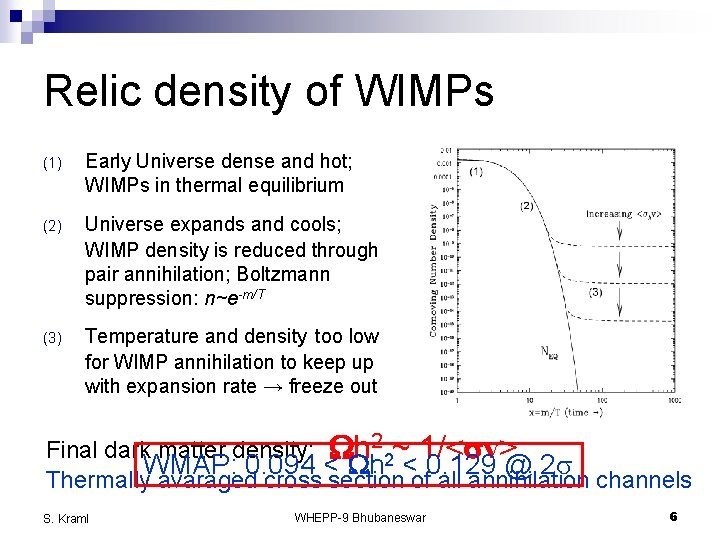
Relic density of WIMPs (1) Early Universe dense and hot; WIMPs in thermal equilibrium (2) Universe expands and cools; WIMP density is reduced through pair annihilation; Boltzmann suppression: n~e-m/T (3) Temperature and density too low for WIMP annihilation to keep up with expansion rate → freeze out Final dark matter density: Wh 2 2~ 1/<sv> WMAP: 0. 094 < Wh < 0. 129 @ 2 s Thermally avaraged cross section of all annihilation channels S. Kraml WHEPP-9 Bhubaneswar 6

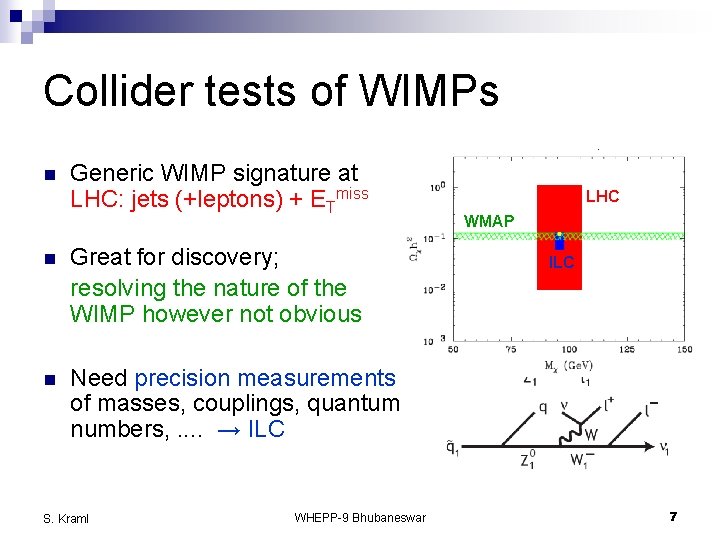
Collider tests of WIMPs n Generic WIMP signature at LHC: jets (+leptons) + ETmiss n Great for discovery; resolving the nature of the WIMP however not obvious n Need precision measurements of masses, couplings, quantum numbers, . . → ILC S. Kraml WHEPP-9 Bhubaneswar LHC WMAP ILC 7

Neutralino-LSP in the MSSM S. Kraml WHEPP-9 Bhubaneswar 8

Minimal supersymmetric model n n SUSY = Symmetry between fermions and bosons SM particles quarks leptons gauge bosons spin Superpartners 1/2 squarks 1/2 sleptons 1 gauginos Higgs bosons 0 higgsinos spin 0 0 1/2 mix to 2 charginos + 4 neutralinos If R-parity is conserved the lightest SUSY particle (LSP) is stable → LSP as cold dark matter candidate S. Kraml WHEPP-9 Bhubaneswar 9

Neutralino system Gauginos Higgsinos Neutralino mass eigenstates → LSP S. Kraml WHEPP-9 Bhubaneswar 10

Neutralino relic density Specific mechanisms to get relic density in agreement with WMAP 0. 094 < Wh 2 < 0. 129 puts strong bounds on the parameter space S. Kraml WHEPP-9 Bhubaneswar 11

m. SUGRA parameter space n GUT-scale boundary conditions: m 0, m 1/2, A 0 [plus tanb, sgn(m)] n 4 regions with right Wh 2 bulk (excl. by mh from LEP) ¨ co-annihilation ¨ Higgs funnel (tanb ~ 50) ¨ focus point (higgsino scenario) ¨ S. Kraml WHEPP-9 Bhubaneswar 12

Prediction of <sv> from colliders: What do we need to measure? n LSP mass and decomposition bino, wino, higgsino admixture n Sfermion masses (bulk, coannhilation) or at least lower limits on them n Higgs masses and widths: h, H, A n tanb With which precision? S. Kraml WHEPP-9 Bhubaneswar 13

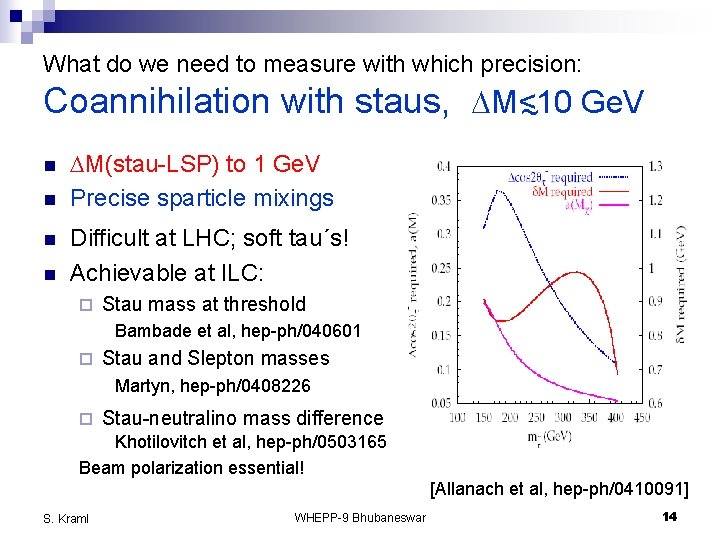
What do we need to measure with which precision: Coannihilation with staus, DM<10 ~ Ge. V n n DM(stau-LSP) to 1 Ge. V Precise sparticle mixings Difficult at LHC; soft tau´s! Achievable at ILC: ¨ Stau mass at threshold Bambade et al, hep-ph/040601 ¨ Stau and Slepton masses Martyn, hep-ph/0408226 ¨ Stau-neutralino mass difference Khotilovitch et al, hep-ph/0503165 Beam polarization essential! [Allanach et al, hep-ph/0410091] S. Kraml WHEPP-9 Bhubaneswar 14

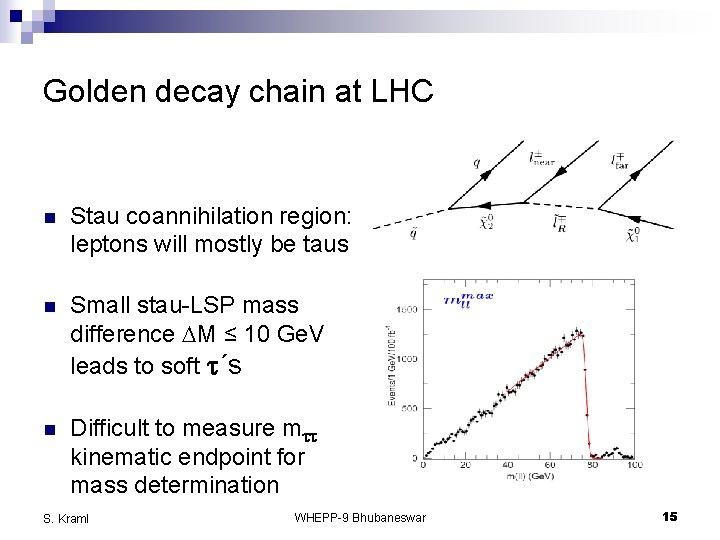
Golden decay chain at LHC n Stau coannihilation region: leptons will mostly be taus n Small stau-LSP mass difference DM ≤ 10 Ge. V leads to soft t´s n Difficult to measure mtt kinematic endpoint for mass determination S. Kraml WHEPP-9 Bhubaneswar 15

Determination of slepton and LSP masses at the ILC [Martyn, hep-ph/0408226] S. Kraml WHEPP-9 Bhubaneswar 16

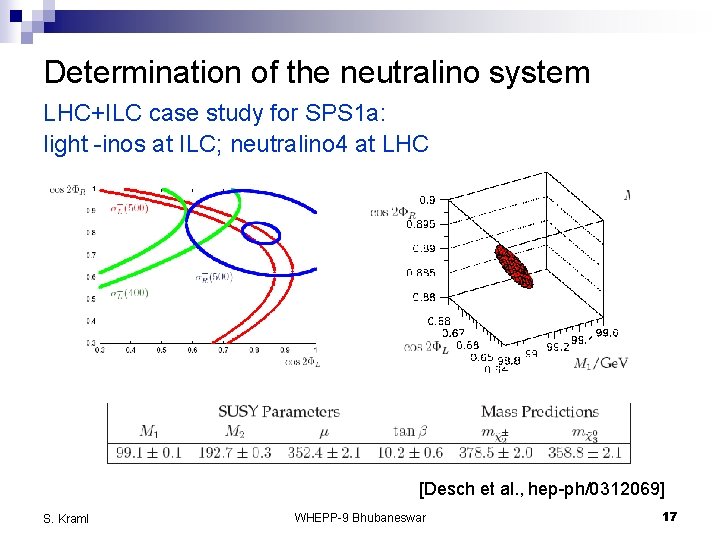
Determination of the neutralino system LHC+ILC case study for SPS 1 a: light -inos at ILC; neutralino 4 at LHC [Desch et al. , hep-ph/0312069] S. Kraml WHEPP-9 Bhubaneswar 17

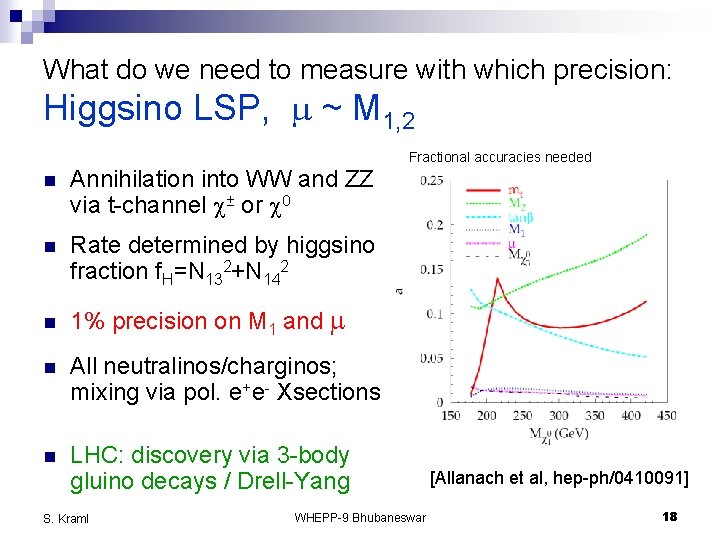
What do we need to measure with which precision: Higgsino LSP, m ~ M 1, 2 n Annihilation into WW and ZZ via t-channel c± or c 0 n Rate determined by higgsino fraction f. H=N 132+N 142 n Fractional accuracies needed 1% precision on M 1 and m n All neutralinos/charginos; mixing via pol. e+e- Xsections n LHC: discovery via 3 -body gluino decays / Drell-Yang S. Kraml WHEPP-9 Bhubaneswar [Allanach et al, hep-ph/0410091] 18

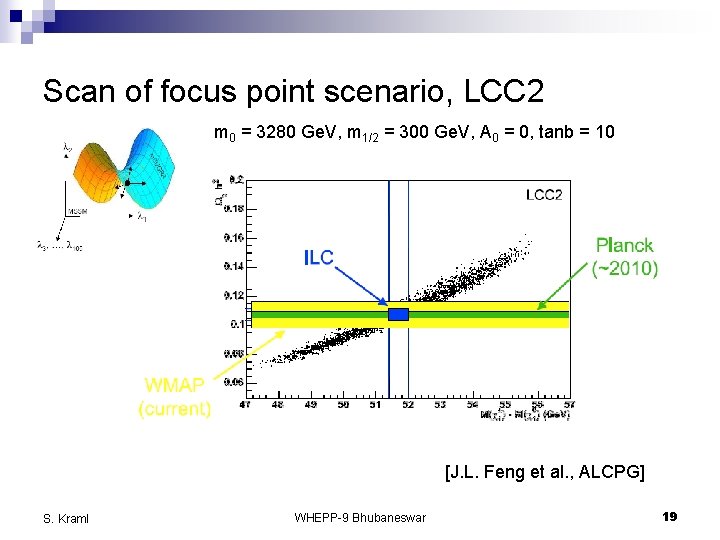
Scan of focus point scenario, LCC 2 m 0 = 3280 Ge. V, m 1/2 = 300 Ge. V, A 0 = 0, tanb = 10 [J. L. Feng et al. , ALCPG] S. Kraml WHEPP-9 Bhubaneswar 19

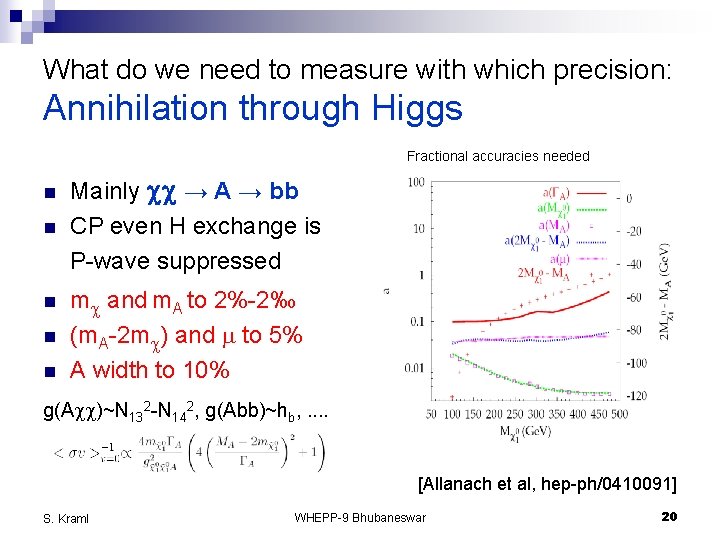
What do we need to measure with which precision: Annihilation through Higgs Fractional accuracies needed n n n Mainly cc → A → bb CP even H exchange is P-wave suppressed mc and m. A to 2%-2‰ (m. A-2 mc) and m to 5% A width to 10% g(Acc)~N 132 -N 142, g(Abb)~hb, . . [Allanach et al, hep-ph/0410091] S. Kraml WHEPP-9 Bhubaneswar 20

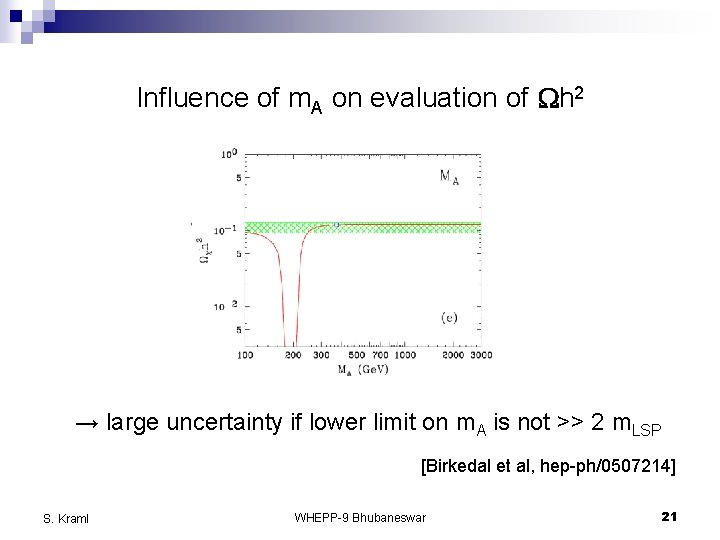
Influence of m. A on evaluation of Wh 2 → large uncertainty if lower limit on m. A is not >> 2 m. LSP [Birkedal et al, hep-ph/0507214] S. Kraml WHEPP-9 Bhubaneswar 21

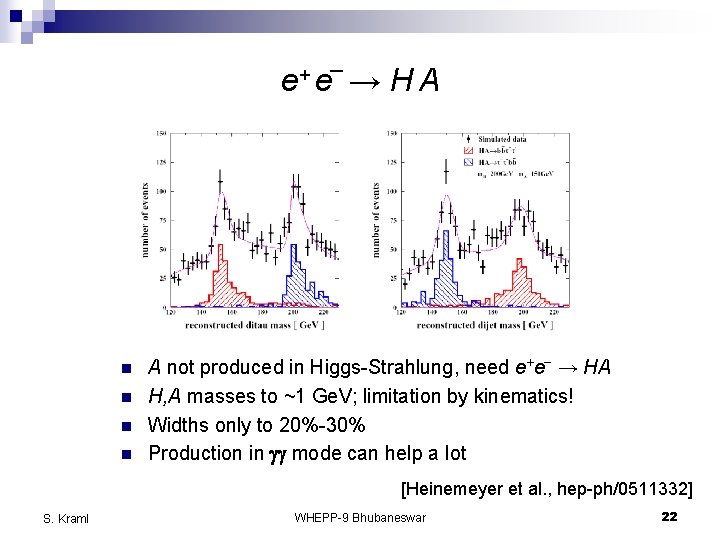
e+ e n n _ → HA e+ e _ A not produced in Higgs-Strahlung, need → HA H, A masses to ~1 Ge. V; limitation by kinematics! Widths only to 20%-30% Production in gg mode can help a lot [Heinemeyer et al. , hep-ph/0511332] S. Kraml WHEPP-9 Bhubaneswar 22

Heavy Higgses at LHC H/A in cascade decays S. Kraml WHEPP-9 Bhubaneswar 23

For a precise prediction of Wh 2 compatible with WMAP acurracy we need precision measurements of most of the SUSY spectrum → LHC/ILC synergy S. Kraml WHEPP-9 Bhubaneswar 24

So far considered CP conserving MSSM What if CP is violated? [we actually need new sources of CP violation beyond the SM for baryogenesis] S. Kraml WHEPP-9 Bhubaneswar 25

CP violation n In the general MSSM, gaugino and higgsino mass parameters and trilinear couplings can be complex: n Important influence on sparticle production and decay rates → Expect similar influence on <sv> NB 1: M 2 can also be complex, but its phase can be rotated away. NB 2: CPV phases are strongly constrained by dipole moments; we set fm=0 and assume very heavy 1 st+2 nd generation sfermions S. Kraml WHEPP-9 Bhubaneswar 26

CP violation: Higgs sector n Non-zero phases induce CP violation in the Higgs sector through loops → mixing of h, H, A: n Couplings to neutralinos: S. Kraml WHEPP-9 Bhubaneswar 27

Previous studies of neutralino relic density with CP violation S. Kraml WHEPP-9 Bhubaneswar 28

CPV analysis with micr. OMEGAs M 1 = 150, M 2 = 300, At = 1200 Ge. V, tanb = 5 masses of 3 rd gen: 500 Ge. V, 1 st+2 nd gen: 10 Te. V n n bino-like LSP, m ~ 150 Ge. V Wh 2 < 0. 129 needs annihilation through Higgs Scenario 1: m = 500 Ge. V → small mixing in Higgs sector Scenario 2: m = 1 Te. V → large mixing in Higgs sector Higgs mixing ~ Im(Atm) [Belanger, Boudjema, SK, Pukhov, Semenov, in: Les. Houches‘ 05] S. Kraml WHEPP-9 Bhubaneswar 29

CPV with micr. OMEGAs S. Kraml WHEPP-9 Bhubaneswar 30

Scenario 2 Key parameter is distance from pole S. Kraml WHEPP-9 Bhubaneswar 31

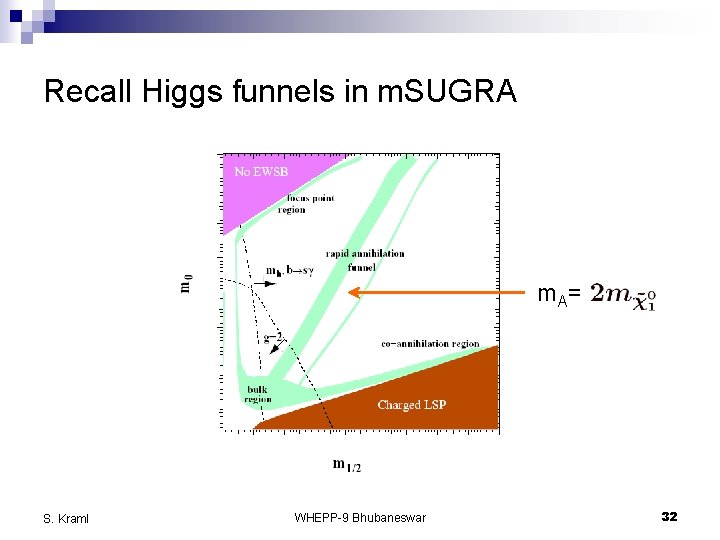
Recall Higgs funnels in m. SUGRA m. A = S. Kraml WHEPP-9 Bhubaneswar 32

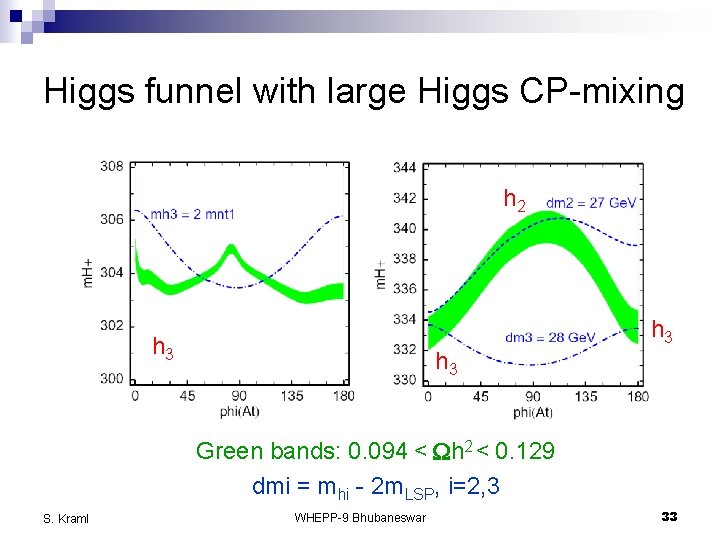
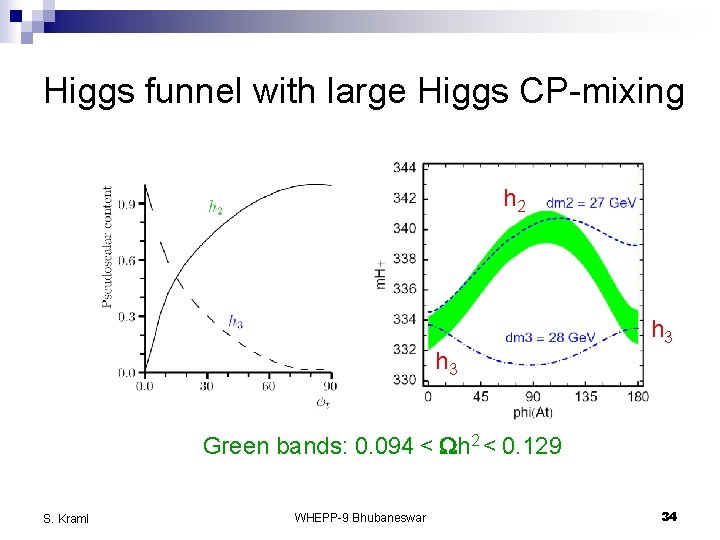
Higgs funnel with large Higgs CP-mixing h 2 h 3 h 3 Green bands: 0. 094 < Wh 2 < 0. 129 dmi = mhi - 2 m. LSP, i=2, 3 S. Kraml WHEPP-9 Bhubaneswar 33

Higgs funnel with large Higgs CP-mixing h 2 h 3 h 3 Green bands: 0. 094 < Wh 2 < 0. 129 S. Kraml WHEPP-9 Bhubaneswar 34

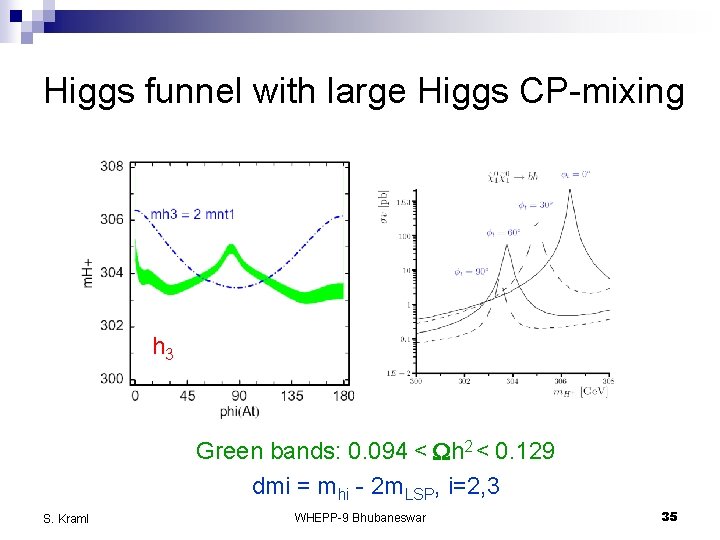
Higgs funnel with large Higgs CP-mixing h 3 Green bands: 0. 094 < Wh 2 < 0. 129 dmi = mhi - 2 m. LSP, i=2, 3 S. Kraml WHEPP-9 Bhubaneswar 35

n CP violation is a very interesting option ¨ can have order-of-magnitude effect on Wh 2 ¨ needs to be tested precisely ¨ n However: computation of annihilation cross sections at only at tree level; radiative corrections may be sizeable! S. Kraml WHEPP-9 Bhubaneswar 36

Assume we have found SUSY with a neutralino LSP and made very precise measurements of all relevant parameters: What if the inferred 2 Wh is too high? S. Kraml WHEPP-9 Bhubaneswar 37

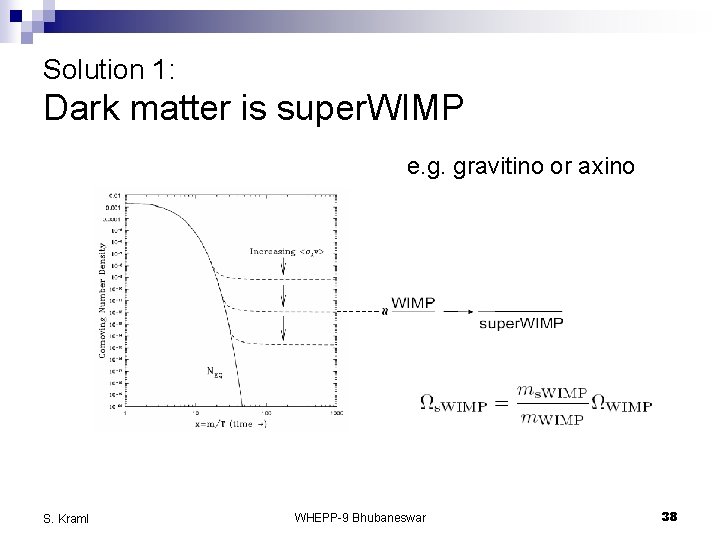
Solution 1: Dark matter is super. WIMP e. g. gravitino or axino S. Kraml WHEPP-9 Bhubaneswar 38

Solution 2: R-parity is violated after all n RPV on long time scales n Late decays of neutralino LSP reduce the number density; actual CDM is something else n Very hard to test at colliders n Astrophysics constraints? S. Kraml WHEPP-9 Bhubaneswar 39

Solution 3: Cosmological assumptions are wrong n n n Our picture of dark matter as a thermal relic from the big bang may be to simple The early Universe may have evolved differently. . . S. Kraml WHEPP-9 Bhubaneswar 40

Conclusions: n We expect new physics beyond the SM to show up at the Te. V energy scale ¨ to provide the dark matter of the Universe ¨ n Using the example of neutralino dark matter I have shown that precison measurements at both LHC+ILC are necessary to pin down the nature and properties of the dark matter Wh 2 ~ 1/<sv> from LHC/ILC ↔ WMAP acurracy n Direct detection in addition to pin down DM S. Kraml WHEPP-9 Bhubaneswar 41

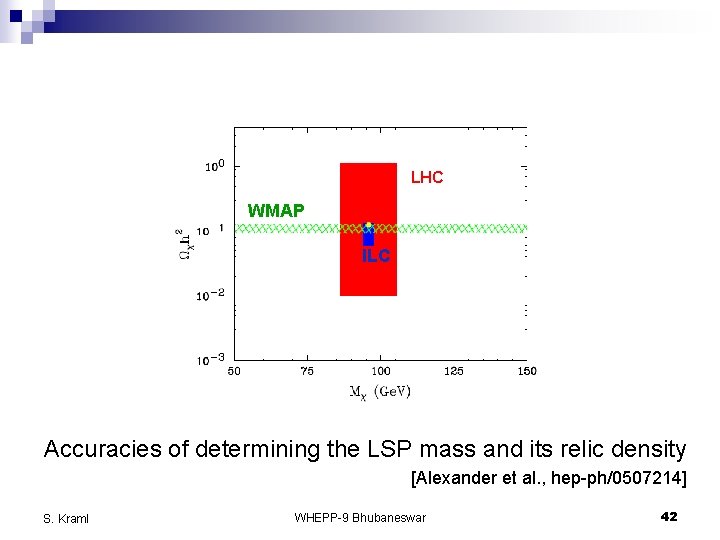
LHC WMAP ILC Accuracies of determining the LSP mass and its relic density [Alexander et al. , hep-ph/0507214] S. Kraml WHEPP-9 Bhubaneswar 42

What if only part of the spectrum is accessible? n Part of the spectrum may escape detection Too heavy sparticles, only limits on masses ¨ Not enough sensitivity, e. g. H, A ¨ Only LHC data available, . . ¨ n Model assumptions, fits of specific models, etc, to obtain testable predicions [or to test models] n Famous example: Fit of m. SUGRA to LHC data at SPS 1 a Need precise predictions within models of SUSY breaking S. Kraml WHEPP-9 Bhubaneswar 43

Comparison of SUSY spectrum codes n Computation of SUSY spectrum with 4 state-of-the-art SUSY codes: Isjet, Softsusy, Spheno, Suspect 2 loop RGEs + 1 loop threshold corrections, 1 loop corr. to Yukawa couplings, . . . n Computation of relic desity with micr. OMEGAs n Mapped m. SUGRA parameter space for ¨ differences in predictions of Wh 2 ¨ differences in WMAP exclusions due to spectrum uncertainties [Belanger, SK, Pukhov, hep-ph/0502079] S. Kraml WHEPP-9 Bhubaneswar 44

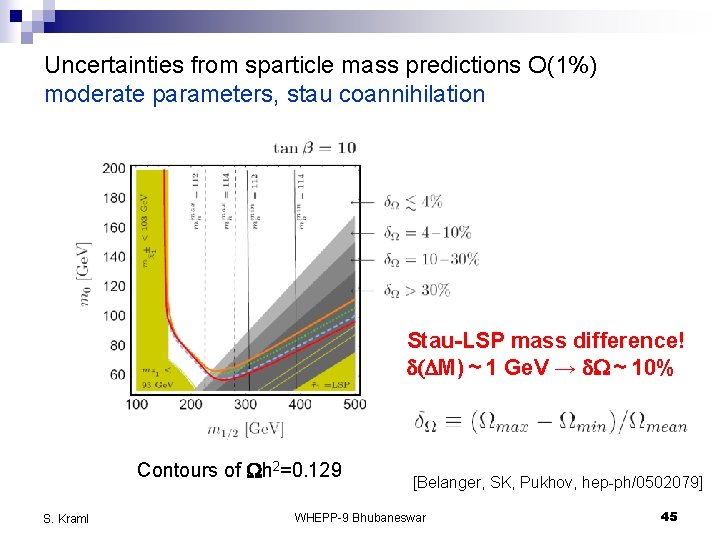
Uncertainties from sparticle mass predictions O(1%) moderate parameters, stau coannihilation Stau-LSP mass difference! d(DM) ~ 1 Ge. V → d. W ~ 10% Contours of Wh 2=0. 129 S. Kraml [Belanger, SK, Pukhov, hep-ph/0502079] WHEPP-9 Bhubaneswar 45

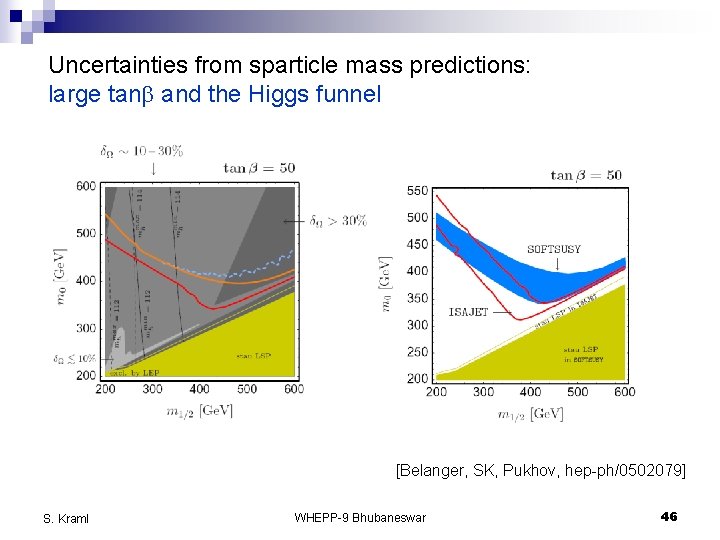
Uncertainties from sparticle mass predictions: large tanb and the Higgs funnel [Belanger, SK, Pukhov, hep-ph/0502079] S. Kraml WHEPP-9 Bhubaneswar 46

n There is need to improve computations and tools in order to match acurracies required by WMAP/Planck Improvements in spectrum computations are discussed in [Baer, Ferrandis, SK, Porod, hep-ph/0511123] S. Kraml WHEPP-9 Bhubaneswar 47