Coupling quantum dots to leads Universality and QPT

Coupling quantum dots to leads: Universality and QPT Richard Berkovits Bar-Ilan University Moshe Goldstein (BIU), Yuval Weiss (BIU) and Yuval Gefen (Weizmann)

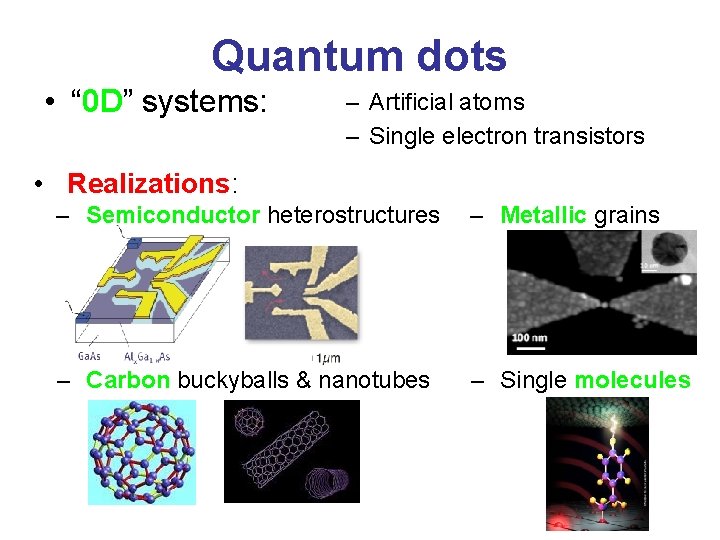
Quantum dots • “ 0 D” systems: – Artificial atoms – Single electron transistors • Realizations: – Semiconductor heterostructures – Metallic grains – Carbon buckyballs & nanotubes – Single molecules

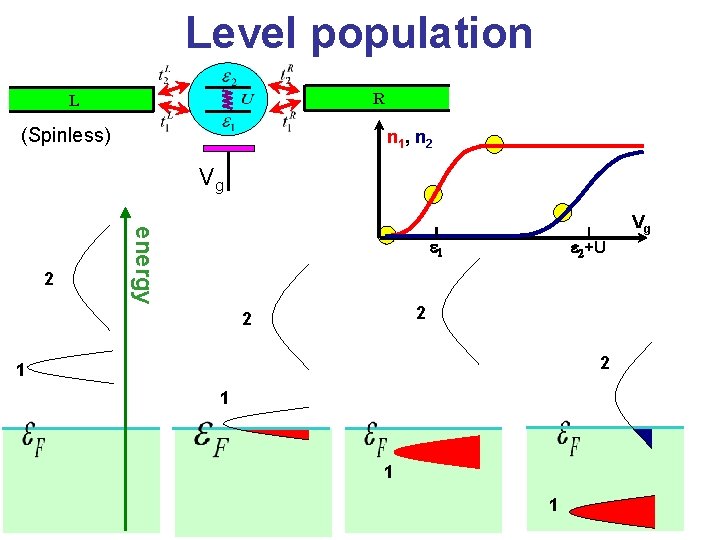
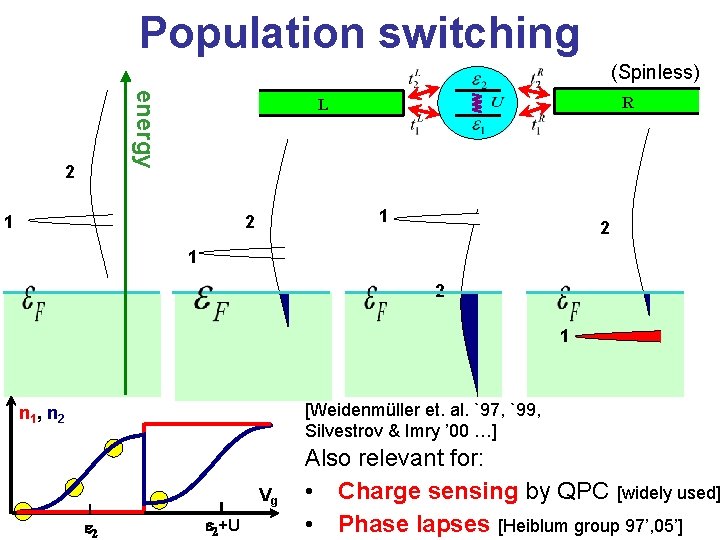
Level population R L (Spinless) n 1 , n 2 Vg energy 2 e 1 e 2+U 2 2 2 1 1 Vg

Population switching (Spinless) energy 2 R L 1 2 1 2 1 [Weidenmüller et. al. `97, `99, Silvestrov & Imry ’ 00 …] n 1 , n 2 Vg e 2+U Also relevant for: • Charge sensing by QPC [widely used] • Phase lapses [Heiblum group 97’, 05’]

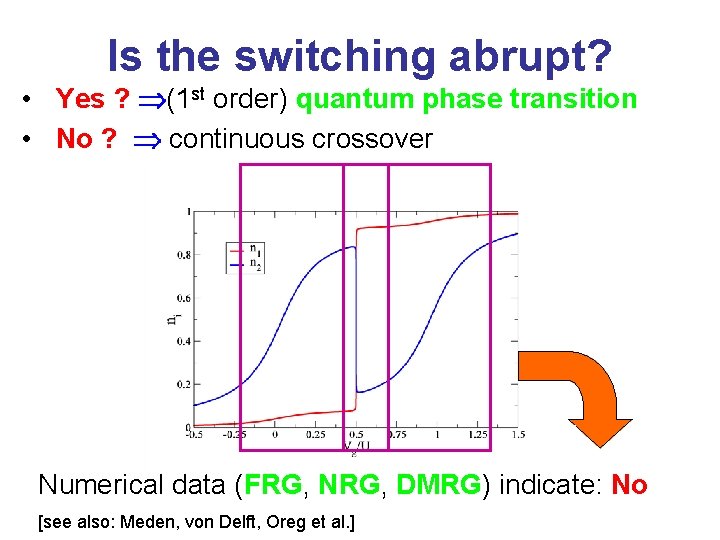
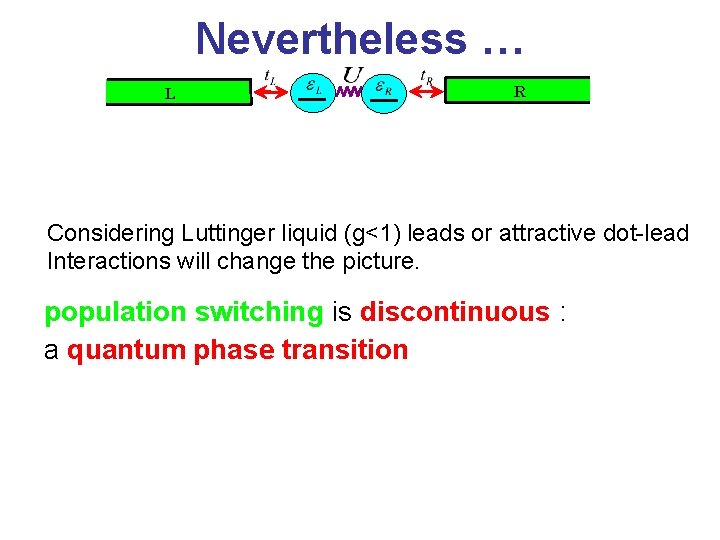
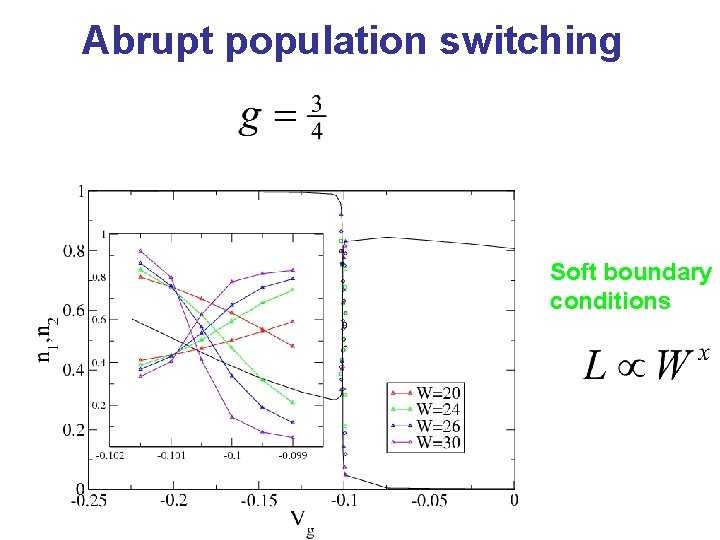
Is the switching abrupt? • Yes ? (1 st order) quantum phase transition • No ? continuous crossover Numerical data (FRG, NRG, DMRG) indicate: No [see also: Meden, von Delft, Oreg et al. ]

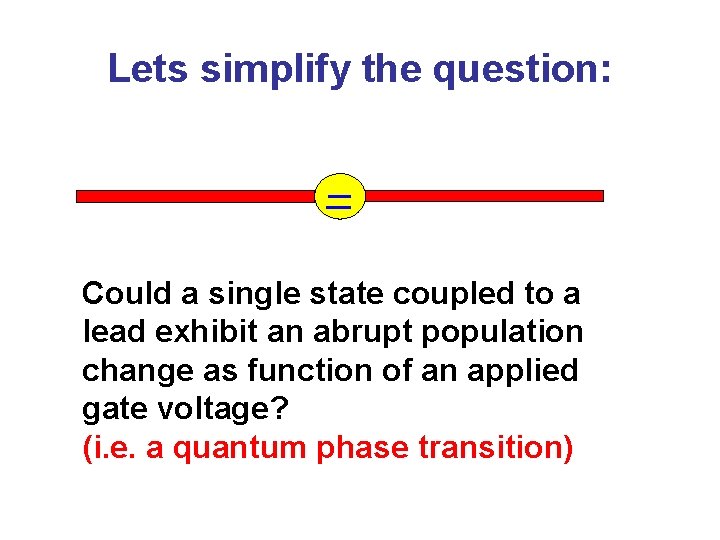
Lets simplify the question: Could a single state coupled to a lead exhibit an abrupt population change as function of an applied gate voltage? (i. e. a quantum phase transition)

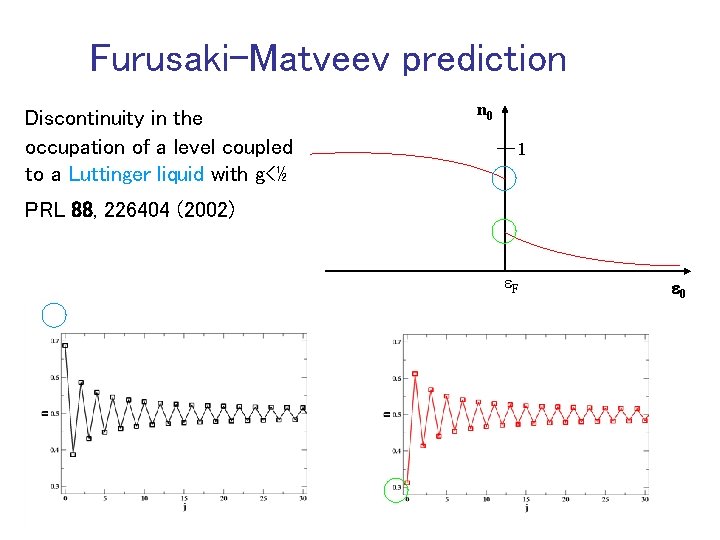
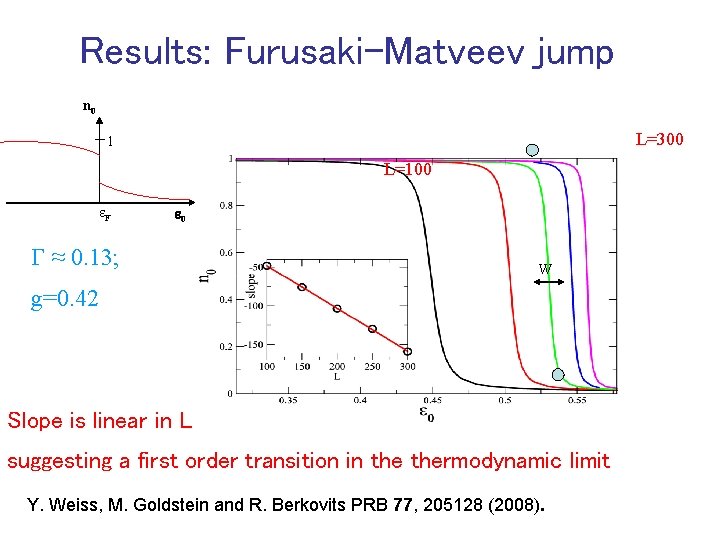
Furusaki-Matveev prediction Discontinuity in the occupation of a level coupled to a Luttinger liquid with g<½ n 0 1 PRL 88, 226404 (2002) e. F e 0

Model • A single level quantum dot coupled to – a Fermi Liquid (FL) – a Luttinger Liquid (LL) – a Charge Density Wave (CDW) • Spinless electrons

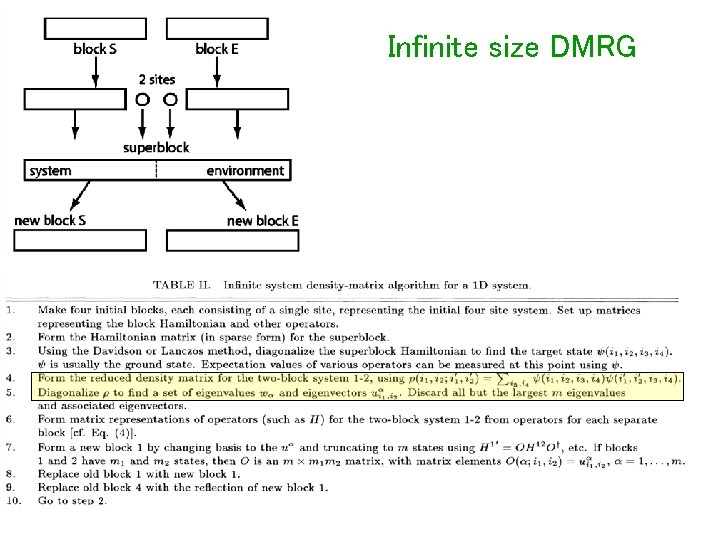
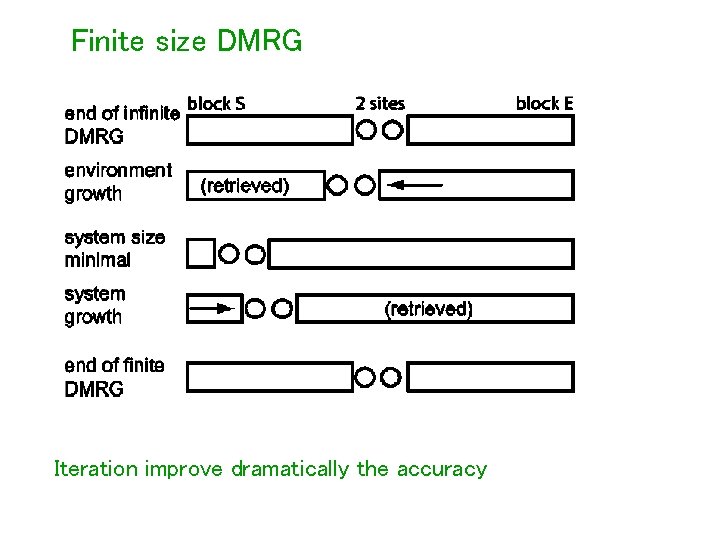
Numerical method: Density Matrix Renormalization Group (DMRG)

Infinite size DMRG

Finite size DMRG Iteration improve dramatically the accuracy

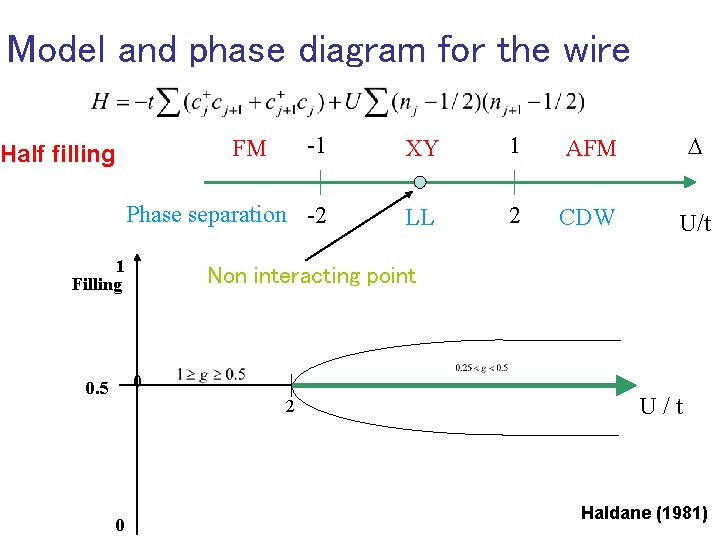
Model and phase diagram for the wire -1 XY 1 AFM D Phase separation -2 LL 2 CDW U/t FM Half filling 1 Filling Non interacting point 0 0. 5 2 0 U/t Haldane (1981)

Evaluating the Luttinger Liquid parameter g g can be evaluated by calculating the addition spectrum and the energy of the first excitation, since By fitting both curves to a polynomial in 1/L and calculating the ratio of the linear coefficients

Results: Furusaki-Matveev jump n 0 L=300 1 L=100 e. F e 0 G ≈ 0. 13; W g=0. 42 Slope is linear in L suggesting a first order transition in thermodynamic limit Y. Weiss, M. Goldstein and R. Berkovits PRB 77, 205128 (2008).

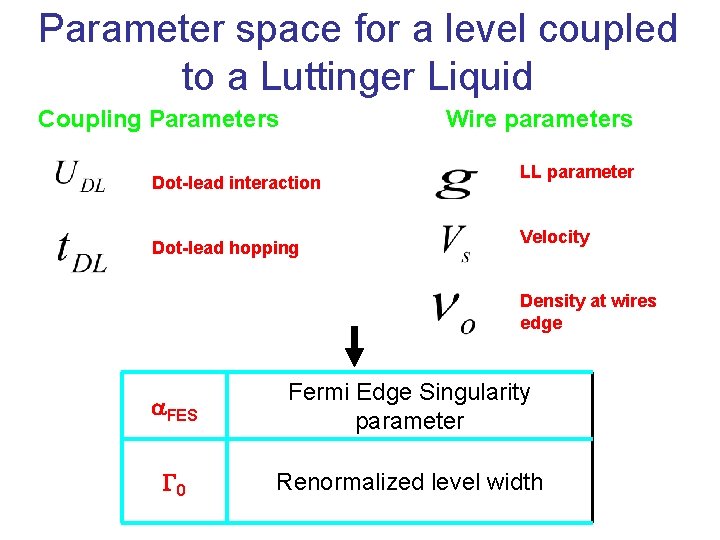
Parameter space for a level coupled to a Luttinger Liquid Coupling Parameters Wire parameters Dot-lead interaction Dot-lead hopping LL parameter Velocity Density at wires edge a. FES Fermi Edge Singularity parameter G 0 Renormalized level width

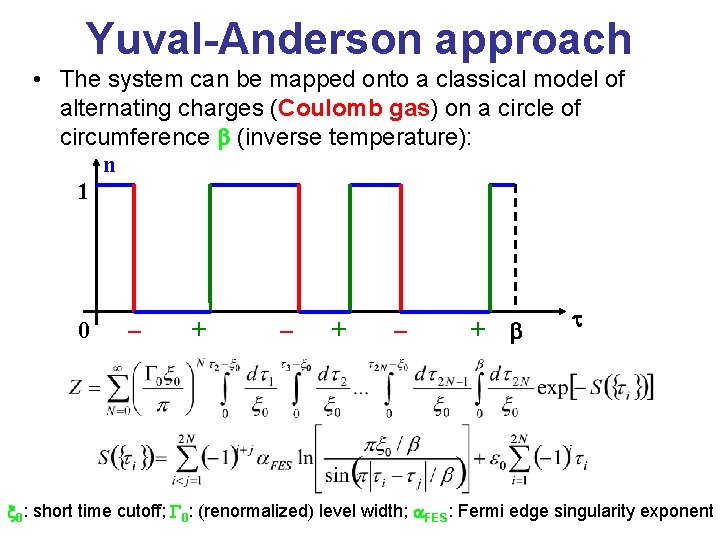
Yuval-Anderson approach • The system can be mapped onto a classical model of alternating charges (Coulomb gas) on a circle of circumference b (inverse temperature): n 1 0 – + – + b t x 0: short time cutoff; G 0: (renormalized) level width; a. FES: Fermi edge singularity exponent

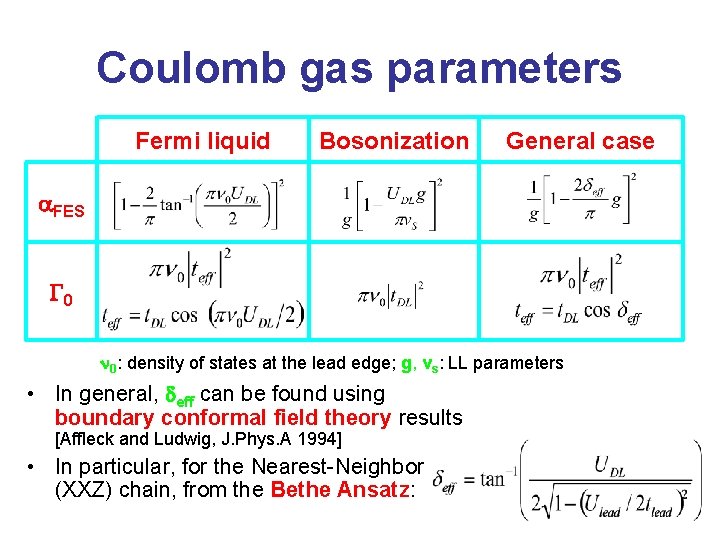
Coulomb gas parameters Fermi liquid Bosonization General case a. FES G 0 n 0: density of states at the lead edge; g, vs: LL parameters • In general, deff can be found using boundary conformal field theory results [Affleck and Ludwig, J. Phys. A 1994] • In particular, for the Nearest-Neighbor (XXZ) chain, from the Bethe Ansatz:

Conclusions from this mapping: Thermodynamic properties, such as population, dynamic capacitance, entropy and heat capacity: • Are universal, i. e. , depend on the microscopic model only through a. FES, G 0 and e 0 • Are identical to their counterparts in the anisotropic Kondo model M. Goldstein, Y. Weiss, and R. Berkovits, Europhys. Lett. 86, 67012 (2009)

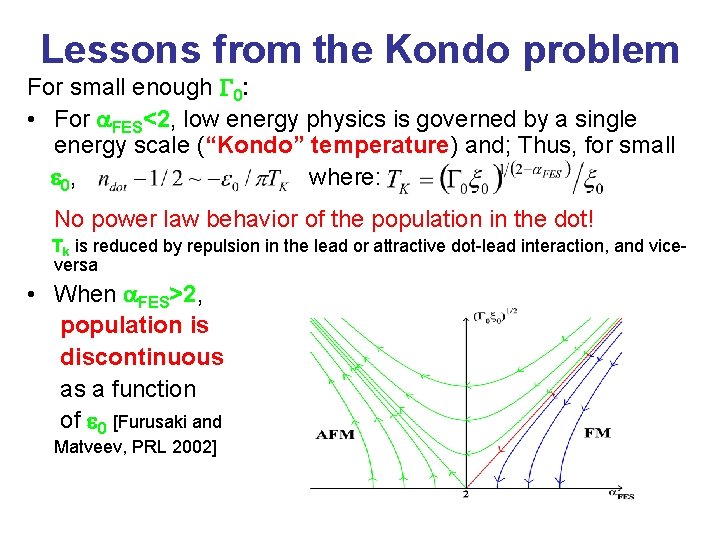
Lessons from the Kondo problem For small enough G 0: • For a. FES<2, low energy physics is governed by a single energy scale (“Kondo” temperature) and; Thus, for small e 0, where: No power law behavior of the population in the dot! Tk is reduced by repulsion in the lead or attractive dot-lead interaction, and viceversa • When a. FES>2, population is discontinuous as a function of e 0 [Furusaki and Matveev, PRL 2002]

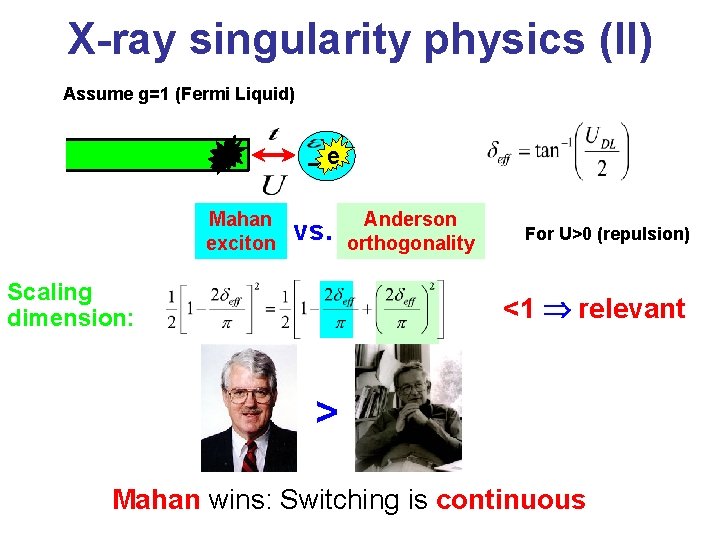
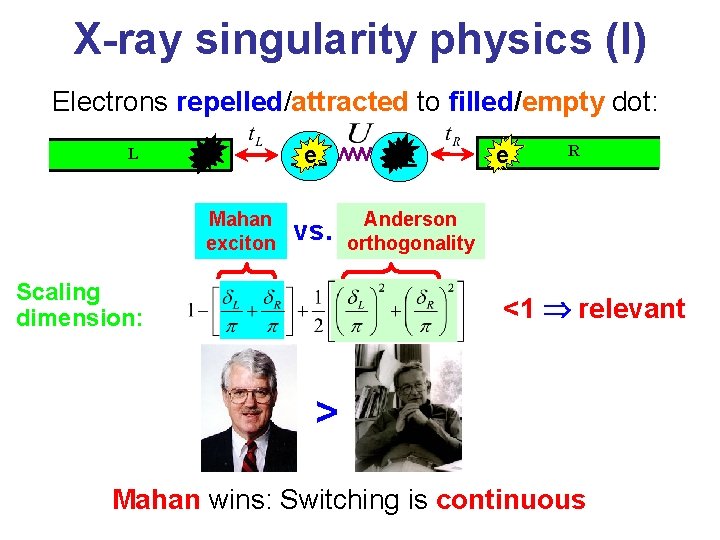
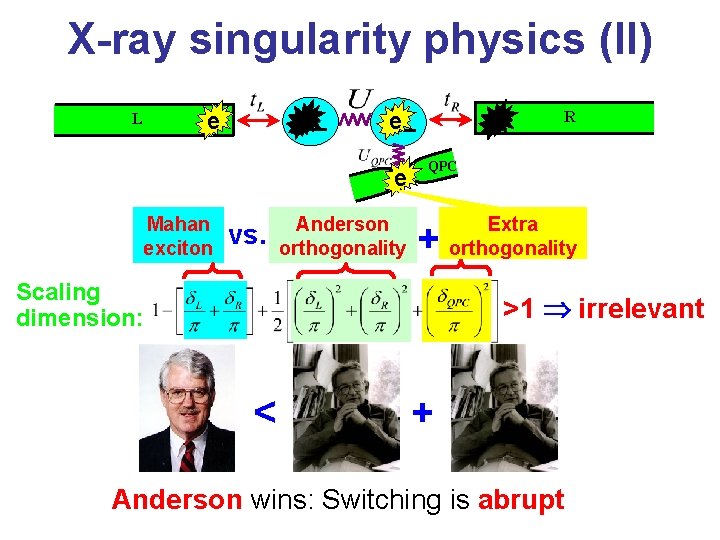
Physical insight: Competition of two effects (I) Anderson Orthogonality Catastrophe, which leads to suppression of the tunneling – zero level width (II) Quasi-resonance between the tunneling electron and the hole left behind (Mahan exciton), which leads to an enhancement of the tunneling – finite level width For a Fermi liquid and no dot-lead interaction (II) wins – finite level width Attractive dot-lead interaction or suppression of LDOS in the lead (LL) suppresses (II) and may lead to (I) gaining the upper hand zero level width

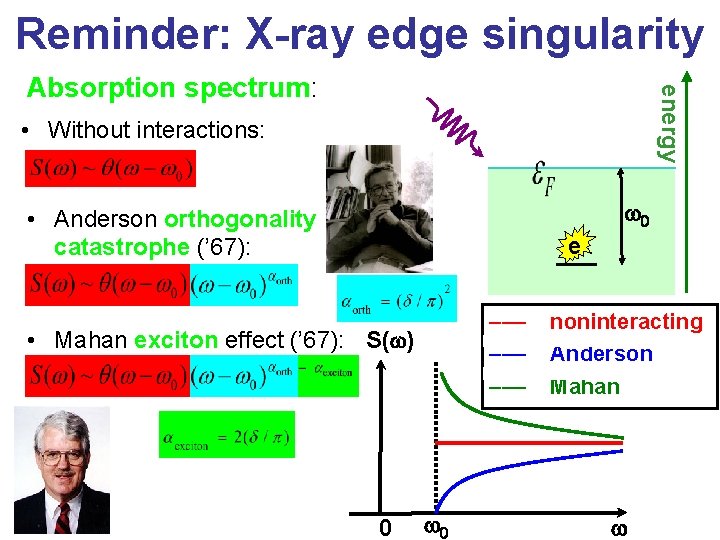
Reminder: X-ray edge singularity energy Absorption spectrum: • Without interactions: w 0 • Anderson orthogonality catastrophe (’ 67): e ––– ––– • Mahan exciton effect (’ 67): S(w) 0 w 0 noninteracting Anderson Mahan w

X-ray singularity physics (II) Assume g=1 (Fermi Liquid) e Mahan exciton vs. Scaling dimension: Anderson orthogonality For U>0 (repulsion) <1 relevant > Mahan wins: Switching is continuous

X-ray singularity physics (III) Assume g=1 (Fermi Liquid) e Mahan exciton e vs. Scaling dimension: Anderson orthogonality For U<0 (attraction) >1 irrelevant < Anderson wins: Switching is discontinuous

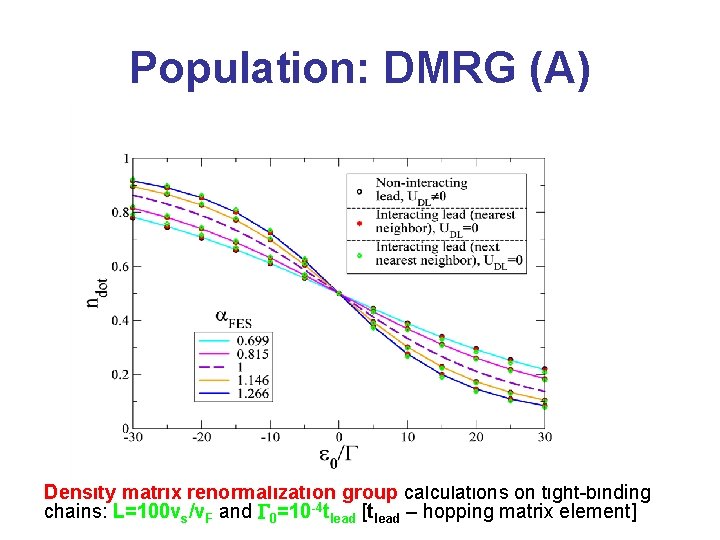
Population: DMRG (A) Density matrix renormalization group calculations on tight-binding chains: L=100 vs/v. F and G 0=10 -4 tlead [tlead – hopping matrix element]

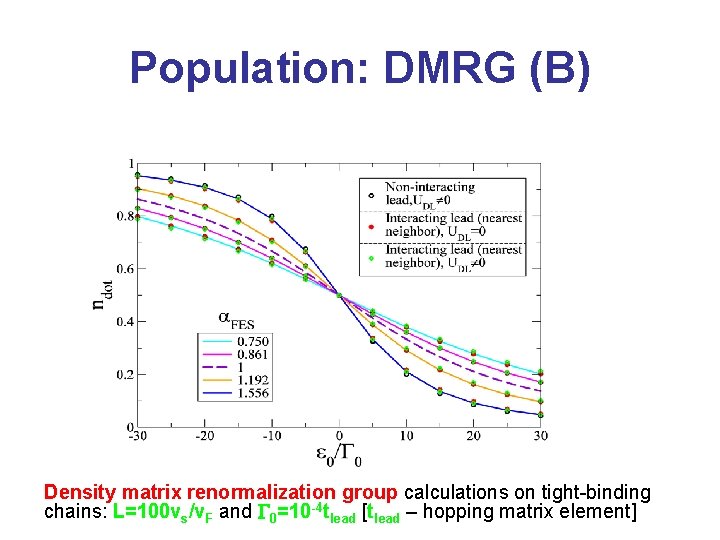
Population: DMRG (B) Density matrix renormalization group calculations on tight-binding chains: L=100 vs/v. F and G 0=10 -4 tlead [tlead – hopping matrix element]

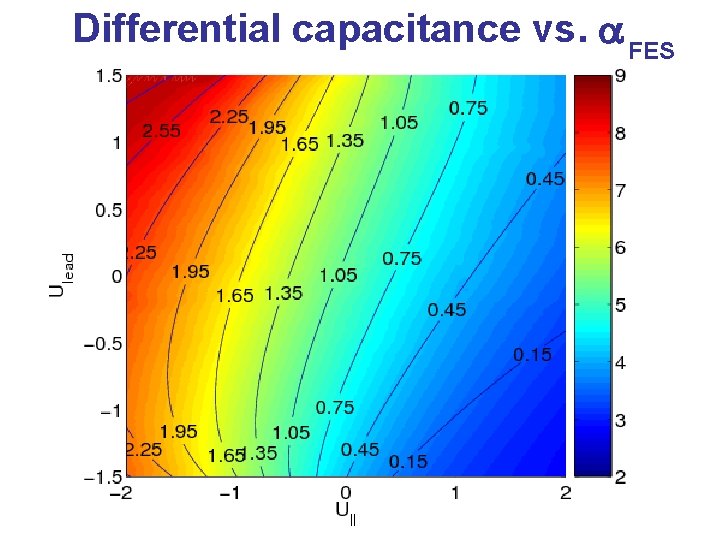
Differential capacitance vs. a FES

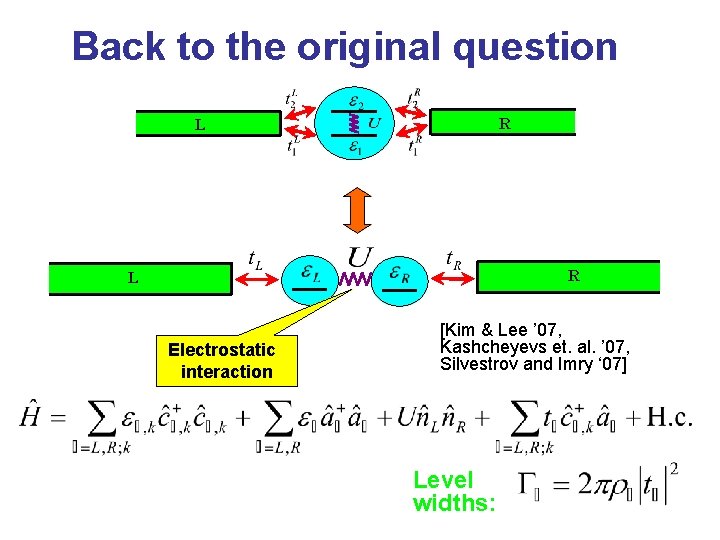
Back to the original question R L Electrostatic interaction [Kim & Lee ’ 07, Kashcheyevs et. al. ’ 07, Silvestrov and Imry ‘ 07] Level widths:

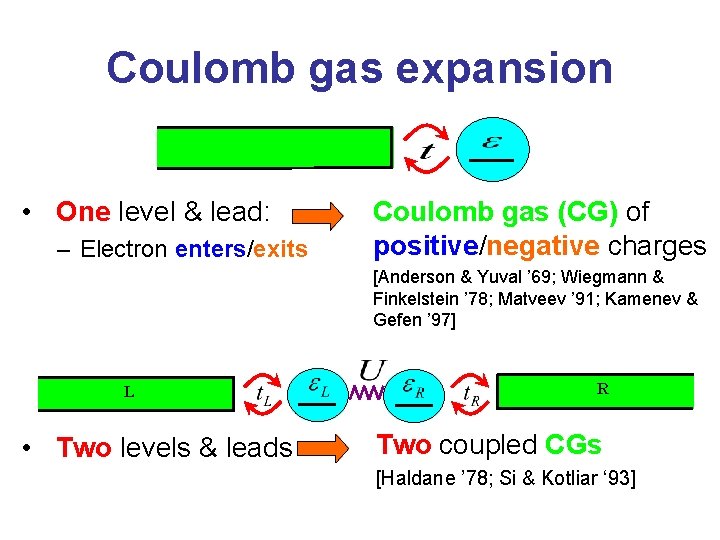
Coulomb gas expansion • One level & lead: – Electron enters/exits Coulomb gas (CG) of positive/negative charges [Anderson & Yuval ’ 69; Wiegmann & Finkelstein ’ 78; Matveev ’ 91; Kamenev & Gefen ’ 97] L • Two levels & leads R Two coupled CGs [Haldane ’ 78; Si & Kotliar ‘ 93]

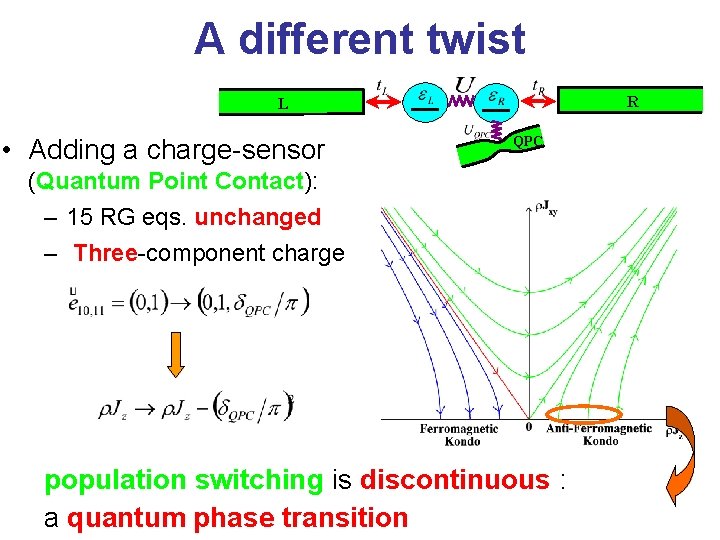
RG analysis • Generically (no symmetries): 15 coupled RG equations [Cardy ’ 81? ] • Solvable in Coulomb valley: • Three stages of RG flow: 11 (I) (II) 10 01 (III) • Result: an effective Kondo model 00

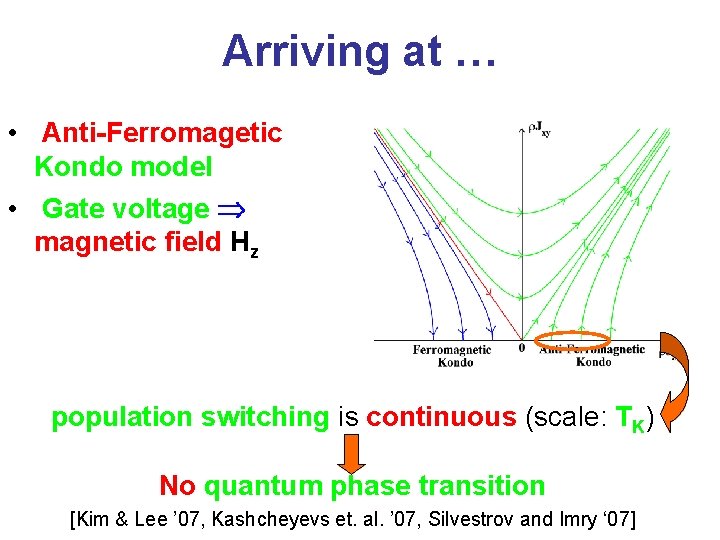
Arriving at … • Anti-Ferromagetic Kondo model • Gate voltage magnetic field Hz population switching is continuous (scale: TK) No quantum phase transition [Kim & Lee ’ 07, Kashcheyevs et. al. ’ 07, Silvestrov and Imry ‘ 07]

Nevertheless … L R Considering Luttinger liquid (g<1) leads or attractive dot-lead Interactions will change the picture. population switching is discontinuous : a quantum phase transition

Abrupt population switching Soft boundary conditions

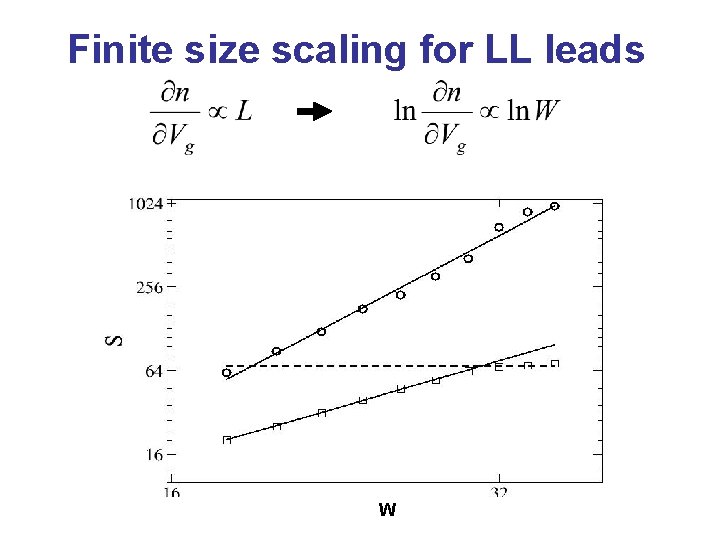
Finite size scaling for LL leads W

A different twist R L • Adding a charge-sensor QPC (Quantum Point Contact): – 15 RG eqs. unchanged – Three-component charge population switching is discontinuous : a quantum phase transition

X-ray singularity physics (I) Electrons repelled/attracted to filled/empty dot: e L Mahan exciton vs. Scaling dimension: e R Anderson orthogonality <1 relevant > Mahan wins: Switching is continuous

X-ray singularity physics (II) e L e Mahan exciton R e vs. Anderson orthogonality QPC + Scaling dimension: Extra orthogonality >1 irrelevant < + Anderson wins: Switching is abrupt

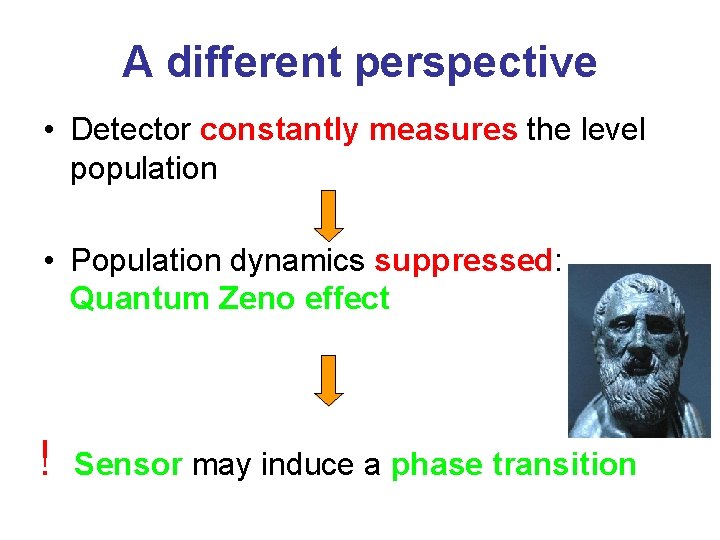
A different perspective • Detector constantly measures the level population • Population dynamics suppressed: Quantum Zeno effect ! Sensor may induce a phase transition

Conclusions • Population switching: a steep crossover, No quantum phase transition • Adding a third terminal (or LL leads): 1 st order quantum phase transition • Laboratory: Anderson orthogonality, Mahan exciton & Quantum Zeno effect