COP 3530 Data Structures Sorting Dr Ron Eaglin

COP 3530 - Data Structures Sorting Dr. Ron Eaglin

Objectives • Understand key elements of sorting algorithms • Select appropriate sorting algorithm for situation • Apply sorting algorithms to data structures

Sorting • Systematically arrange items into groups or in a specific order. • A sorting algorithm puts elements in a list in a specific order • Some algorithms are old, but newer algorithms have been introduced (Timsort, 2002) (Library Sort, 2006)

Evaluating Sorting • Computational Complexity (as expressed by Big O) • Computational Complexity of swaps • Memory use • Stability • Comparison operators

Sorting Stability • IF two items to be sorted are equivalent, their relative order will be preserved. • Not a problem if all items are unique • Sometimes a secondary comparison is used as a tie-breaker

Algorithms used in sorting - Swap function swap(a, b) { var temp = a; a = b; b = temp; } Swaps actual variables

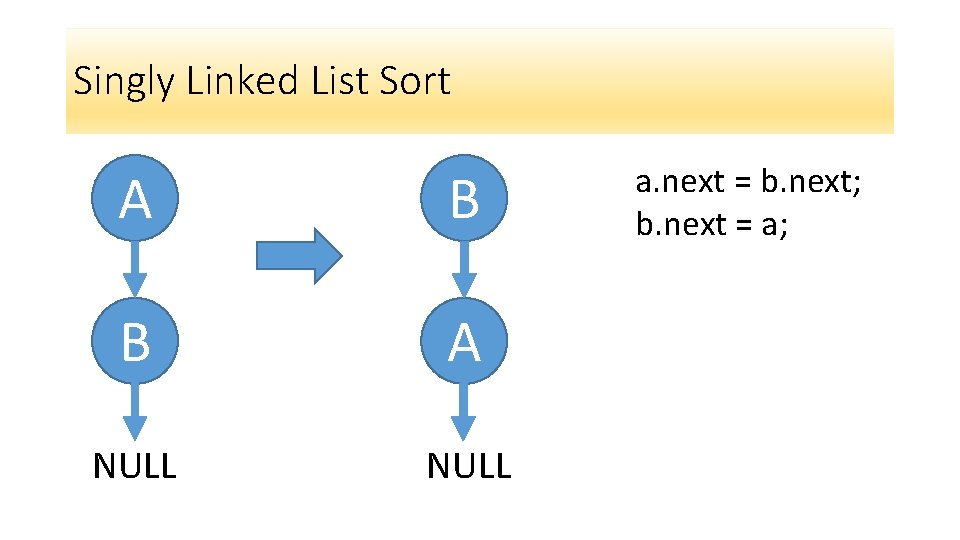
Singly Linked List Sort A B B A NULL a. next = b. next; b. next = a;

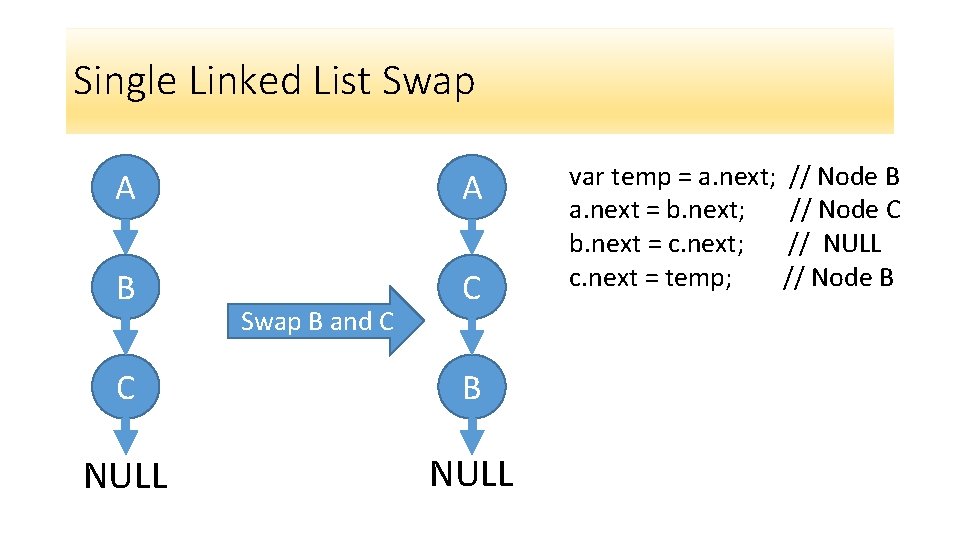
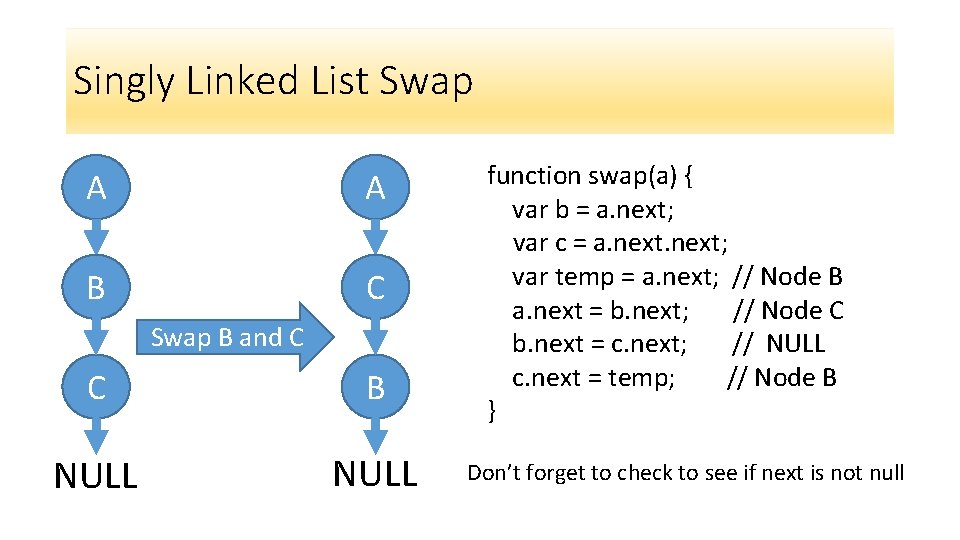
Single Linked List Swap A A B C Swap B and C C B NULL var temp = a. next; // Node B a. next = b. next; // Node C b. next = c. next; // NULL c. next = temp; // Node B

Singly Linked List Swap A A B C Swap B and C C B NULL function swap(a) { var b = a. next; var c = a. next; var temp = a. next; // Node B a. next = b. next; // Node C b. next = c. next; // NULL c. next = temp; // Node B } Don’t forget to check to see if next is not null

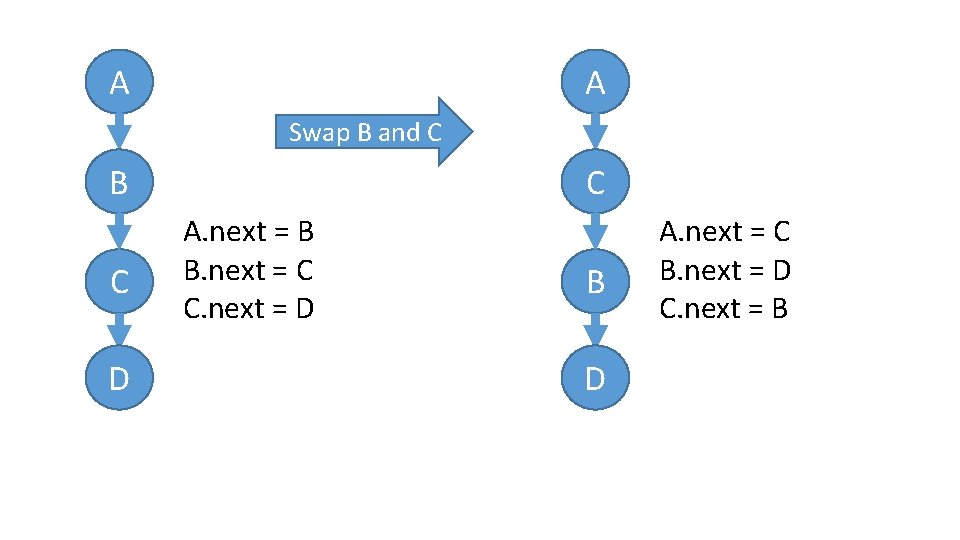
A A Swap B and C B C D C A. next = B B. next = C C. next = D B D A. next = C B. next = D C. next = B

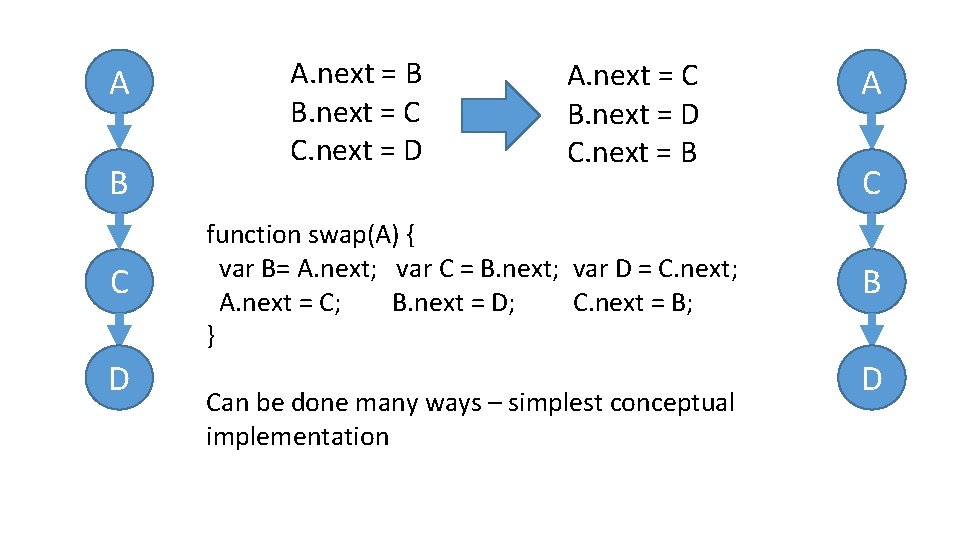
A B C D A. next = B B. next = C C. next = D A. next = C B. next = D C. next = B function swap(A) { var B= A. next; var C = B. next; var D = C. next; A. next = C; B. next = D; C. next = B; } Can be done many ways – simplest conceptual implementation A C B D

Swapping • Alternately the contents of the node can be swapped. • Implementation for singly linked list, also doubly linked lists or other architectures. • Swap is key to some algorithms.

Swapping Contents function swap( a, b) { var c = a. value; a. value = b. value; b. value = c; } Much simpler conceptually than switching pointers – but… if other properties are attached to node – will be left behind.

Bubble Sort • Simplest of sorting algorithms • O(n^2) • Uses swap set swapped Boolean to false iterate through list if node. value > node. next. value swap nodes set swapped Boolean to true Repeat until no swaps made

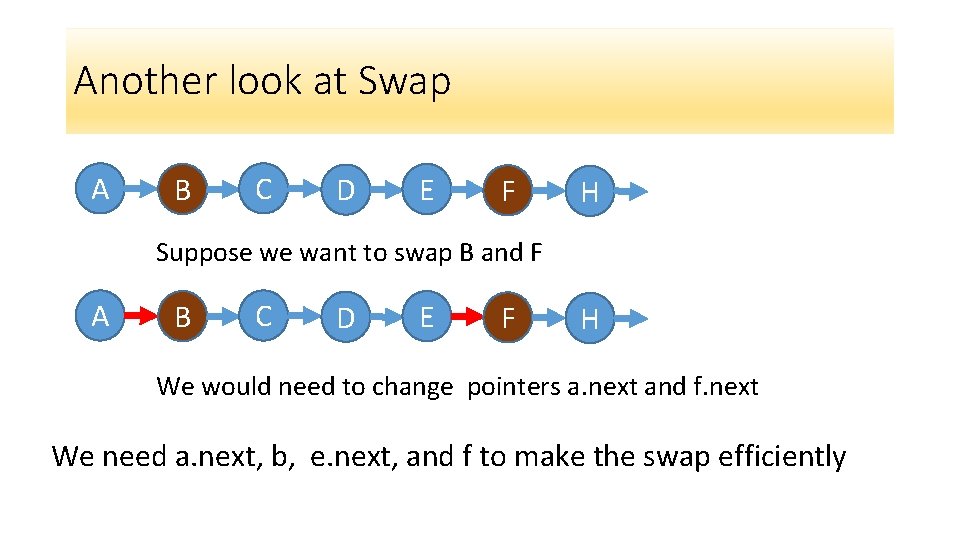
Another look at Swap A B C D E F H Suppose we want to swap B and F A B C D E F H We would need to change pointers a. next and f. next We need a. next, b, e. next, and f to make the swap efficiently

Quick. Sort Algorithm • Average Case Complexity O(n log n) and In-Place algorithm • Steps • 1. Pick a Pivot from the array • 2. Rearrange array so all elements < pivot are before, all elements > are after • 3. Re-apply steps 1 and 2 recursively on the sub-arrays. • Plenty of tutorials online – follow step-by-step

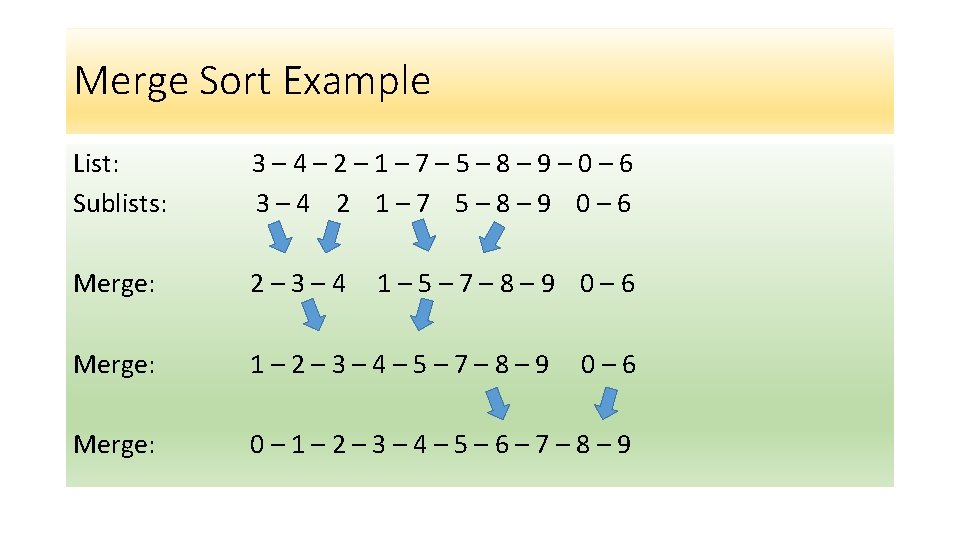
Merge Sort • O( n log n) worst case complexity, NOT In-place algorithm • Steps • 1. Divide the unsorted list into n sublists • 2. Merge sorted sublists into new sorted sublists • Relies on efficient Merge algorithm

Merge Sort Example List: Sublists: 3– 4– 2– 1– 7– 5– 8– 9– 0– 6 3– 4 2 1– 7 5– 8– 9 0– 6 Merge: 2– 3– 4 Merge: 1– 2– 3– 4– 5– 7– 8– 9 Merge: 0– 1– 2– 3– 4– 5– 6– 7– 8– 9 1– 5– 7– 8– 9 0– 6

Efficiency and Performance • Algorithm Worst Case and Average performance is important • Efficiency of sub-algorithms are important (swap, merge) • Differences for different structures

Sorting Algorithms • Full outline on Wikipedia • https: //en. wikipedia. org/wiki/Sorting_algorithm • Best, average, and worst case complexity • Memory requirements • Stable • Limitations for various structures

Objectives • Understand key elements of sorting algorithms • Select appropriate sorting algorithm for situation • Apply sorting algorithms to data structures