Convexity of Point Set Sandip Das sandipdasisical ac

Convexity of Point Set Sandip Das (sandipdas@isical. ac. in) Indian Statistical Institute

Convex Set set C d is convex if for every two points a, b C, the line segment joining a and b is also contained in C. �A

Convex Set (Contd. ) set C d is convex if for every two points a, b C, the line segment joining a and b is also contained in C. �A set C d is convex if for every two points a, b C, and for every t [0, 1], the point t. a + (1 - t). b belongs to C. �A Are These Two Definitions Equivalent?

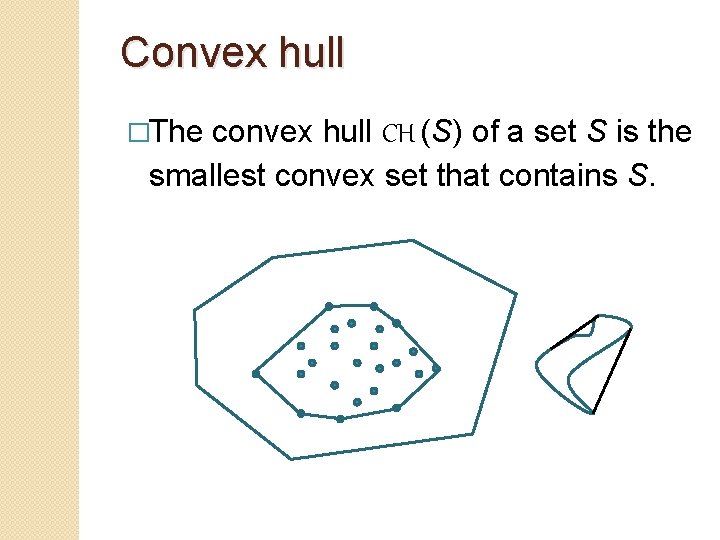
Convex hull �The convex hull CH (S) of a set S is the smallest convex set that contains S.

Convex hull (Contd. ) �Intersection of all convex set containing S. Algebraic Observation: A point a belongs to CH (S) iff there exist points s 1, s 2, . . . , sn S, and=1 nonnegative real number t 1, t 2, . . . , tn with =1 n i ti =1 n such that a = i ti. si

Convex hull: Application in optimization Consider the following Database Person income … … Queries: expenditure … Find person having maximum income Find person whose expenditure is minimum Find person having maximum savings

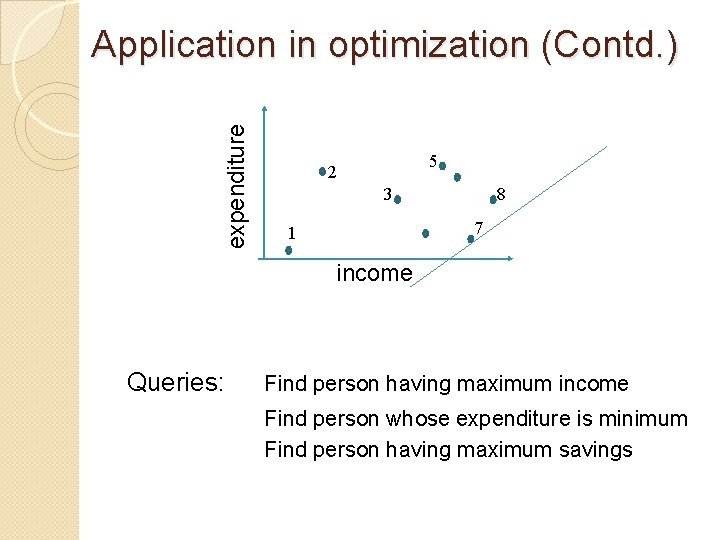
expenditure Application in optimization (Contd. ) 5 2 3 8 7 1 income Queries: Find person having maximum income Find person whose expenditure is minimum Find person having maximum savings

Linear Programming Maximizing c 1 x 1+ c 2 x 2+. . . + cn xn Subject to a 11 x 1+ a 12 x 2+. . . + a 1 n xn ≤ b 1 a 21 x 1+ a 22 x 2+. . . + a 2 n xn ≤ b 2 … an 1 x 1+ an 2 x 2+. . . + ann xn ≤ bn

Linear Programming (Contd. ) a 11 x 1+ a 12 x 2+. . . + a 1 n xn = b 1 is a hyperplane in n dimensional plane a 11 x 1+ a 12 x 2+. . . + a 1 n xn ≤ b 1 fe a sib le so lut ion Implies a halfplane bounded by this hyperplane

Linear Programming (Contd. ) Set of constraints generate intersection of n hyperplanes Intersection of convex regions is convex to g g ant. n i nd sett nst o sp by e co e r or eria som c e crit as n pla tion lue r pe iza l va y H tim na op ctio fun

Linear Programming (Contd. ) Set of constraints generate intersection of n hyperplanes Intersection of convex regions is convex Intersection region may be empty => no solution Intersection region may be unbounded => it may generate unbounded optimal solution

Center point Looking for center point among points arranged on a line. Have a sense of center point but not clear - Mean ? -Median ?

Center point (Contd. ) Observe that Median say x is such a point where | # of points on left of x - # of points on right of x| ≤ 1 We want to extend this idea in 2 D n points in a plane.

Center point (Contd. ) n points in a plane. Left and right is not well defined on plane. We can define left and right with respect to a line l Left side of l right side of l

Center point (Contd. ) Consider a point x in 2 D Draw a line l through x. We can compute # of points on left with respect to l Similarly # of points on right with respect to l So, | # of points on left of l - # of points on right of l | varies as the line l rotate and passing through x x l

Center point (Contd. ) | # of points on left of l - # of points on right of l | What is the maximum value of this difference for all line l passing through x x l Let us say that value as c(x)

Center point (Contd. ) The term c(x) may be considered as a measure of x for being a center Can you identify a point x such that c(x) is less than equal to 1? x

Center point (Contd. ) For any point set Can you identify a point x such that c(x) is less than equal to 1? Does such a point always exist?

Center point (Contd. ) Example: Let the point set be Can you identify a point x such that c(x) ≤ 1 x x x

Centerpoint Theorem A point x Rd is called a centerpoint of a point set if each closed halfspace containing x contains at least n/(d+1) points of the point set. Theorem: Each finite point set in Rd has at least one centerpoint. Follows from Helly’s theorem.

Helly’s Theorem Let C 1, C 2, …, Cn be convex sets in 2 D plane. Suppose that the intersection of every 3 of these sets is nonempty. Then the intersection of all the Ci is nonempty.

Proof of Centerpoint Theorem Consider any point set with n points. Take all convex set containing at least 2 n/3 points. Number of such convex sets are finite. Observe that intersection of any three of them is not null Hence, from Helly’s theorem, intersection of all such convex hull is not null. Any point on that intersection is the centerpoint.

Algorithm for finding centerpoint Shreesh Maharaj et al. proposed an excellent algorithm in O(n) time Prune and search technique T(n) = T(c. n) +O(n), 0< c <1 Generate a convex region such that centerpoint region of point set including vertices of convex region is a superset of earlier one If some vertices of that convex region is discarded centerpoint remains same. Discard that fraction of boundary points, and continue the process.

Convex independent set A set S Rd is convex independent if all points in S lie on convex hull of S That is for every x S, x conv{S{x}} Let P be a set of points and the points be in general position. Any three point subset is convex independent But any subset of 4 points is not convex independent

Convex independent set (contd. ) Suppose the set P contains 5 point May we always get a subset of size 4 that are convex independent? Size of convex hull will be either 3, 4 or 5 If the size of convex hull is 5, then … …

Ramsey Theorem G(V, E) is a graph with |V|=6, then either G or Gc must have a triangle. So, R(3, 3) = 6 If the number of vertices is sufficiently large, there always exist a k vertex subset Y such the all hyperedge of 4 vertices is in G or in Gc.

Erdös-Szekeres Theorem Given n points set, color a 4 tuple red if its 4 points are convex independent and blue otherwise. From Ramsey Theorem, there is a k point subset such that all hyperedge is same color. But for k ≥ 5, this color cannot be blue. So, that k point subset is convex independent

Erdös-Szekeres Theorem (Contd. ) For every natural number k, there exist a number n(k) such that any n(k) point set in the plane in general position contains a k-point convex independent subset. 2 k-2 + 1 ≤ n(k) ≤ 2 k-5 Ck-2 - 2

K-Hole Let X be a set of point. A k-point set Y is called a khole in the point set if Y is convex independent and conv(Y) X = Y. Erdös raised the question about the size of point set for k-hole 3 -hole? 4 -hole? 5 -hole? 6 -hole? 7 -hole … … Does not exist.

A lot of questions remain unanswered….