Constructive Methods of Optimal Control under Uncertainty Rafail










![Control System under Disturbances T=[t*, t*] : control interval Dynamical system with disturbance : Control System under Disturbances T=[t*, t*] : control interval Dynamical system with disturbance :](https://slidetodoc.com/presentation_image_h2/fbc90baef589b2652ef9655c24c64807/image-15.jpg)
















- Slides: 44

Constructive Methods of Optimal Control under Uncertainty Rafail Gabasov Belarussian State University NATO ARW, October 21 -25

Outline Introduction 1. Classical optimal feedback and its realization 2. Optimal guaranteeing feedbacks 3. Optimal control under imperfect information 4. Optimal decentralized control 5. Parallelizing of computations during optimal control of large systems 6. Optimal on-line control with delays 7. Optimal control of time-delay systems 8. Optimal control of PDEs 9. Nonlinear optimal control problems 10. Stabilization of dynamical systems Gabasov 2 NATO ARW, October 21 -25

Introduction Points of view on Optimal Control Theory n Calculus of Variations n Control Theory Principles of control n Open-loop control n Closed-loop control n Real time (on-line) control Types of closed loops n Feedforward n Feedback n Feedforward-feedback (combined) Gabasov 3 NATO ARW, October 21 -25

Linear optimal control problem (1) state of the control system at the instant t value of control at the instant t piecewise continuous matrix functions terminal set (g*, g* Rm, H Rm n) set of accessible values of control Discrete controls (h=(t* – t*)/N, N>0): (2) Gabasov 4 NATO ARW, October 21 -25

Classical optimal feedback Imbed problem (1) into a family (3) depending on Th and z Rn u 0(t| , z), t T( ) : optimal open-loop control of (3) for a position ( , z) X : set of states z for which optimal open-loop control exists Optimal feedback : (4) Gabasov 5 NATO ARW, October 21 -25

Realization of optimal feedback Real system closed by optimal feedback: (5) w : disturbances Trajectory of (5) is a solution to linear differential equation: (6) Particular control process with w*(t), t T: (7) Realization of optimal feedback in a particular control process: (8) Gabasov 6 NATO ARW, October 21 -25

Optimal Controller : (9) Linear programming problem: (10) Gabasov 7 NATO ARW, October 21 -25

Fast algorithms for optimal open-loop control n Gabasov R. , Kirillova F. M. (2001) Fast algorithms for positional optimization of dynamic systems. Proceedings of the Workshop "Fast solutions of discretized optimization problems". (K. -H. Hoffmann, R. Hoppe and V. Schulz eds. ) n Gabasov R. , Kirillova F. M. and N. V. Balashevich (2000). On the Synthesis Problem for Optimal Control Systems. SIAM J. Control Optim. n Gabasov, R. , F. M. Kirillova and N. V. Balashevich (2000). Open-loop and Closed-loop Optimization of Linear Control Systems. Asian Journal of Control. Gabasov 8 NATO ARW, October 21 -25

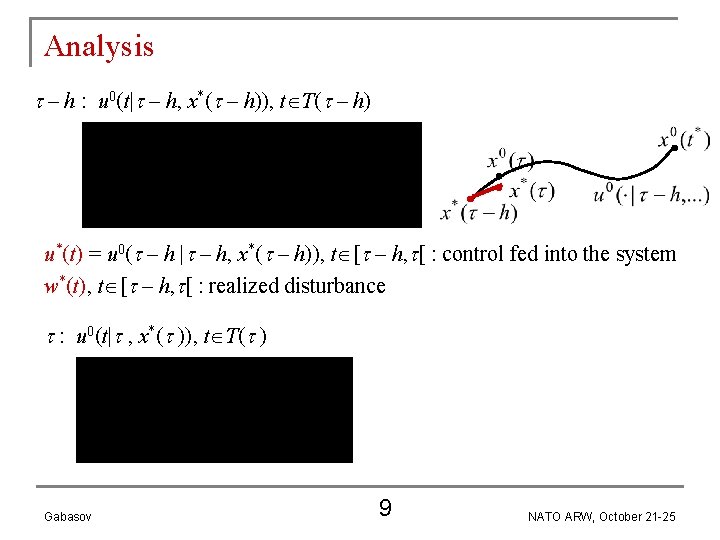
Analysis – h : u 0(t| – h, x*( – h)), t T( – h) u*(t) = u 0( – h | – h, x*( – h)), t [ – h, [ : control fed into the system w*(t), t [ – h, [ : realized disturbance : u 0(t| , x*( )), t T( ) Gabasov 9 NATO ARW, October 21 -25

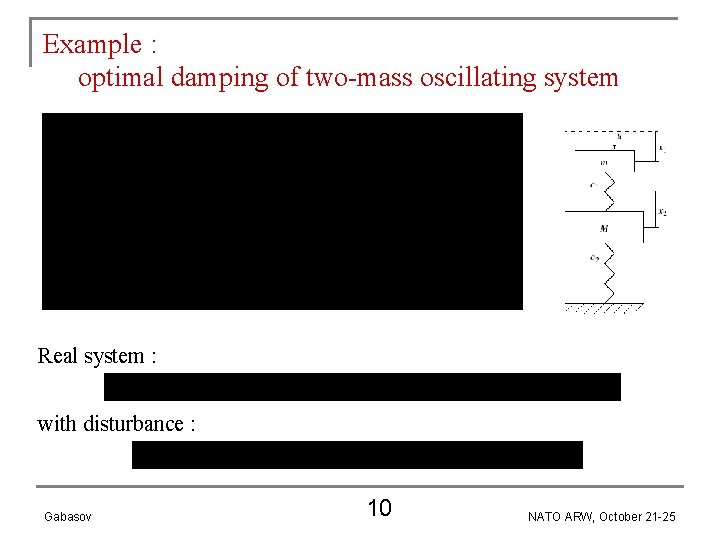
Example : optimal damping of two-mass oscillating system Real system : with disturbance : Gabasov 10 NATO ARW, October 21 -25

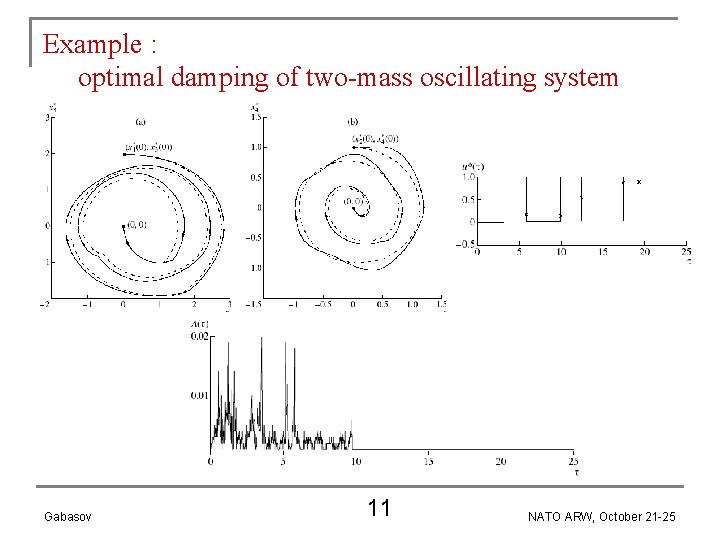
Example : optimal damping of two-mass oscillating system Gabasov 11 NATO ARW, October 21 -25

Discussion n Direct control system q q q n No state or mixed constraints q n n Gabasov R. , Dmitruk N. M. and F. M. Kirillova (2004). Indirect Optimal Control of Dynamical Systems. Comput. Math. Phys. Gabasov R. , Kirillova F. M. and N. S. Pavlenok (2003). Design of Optimal Feedbacks in the Class of Inertial Controls. Automation and Remote Control Gabasov R. , Kirillova F. M. and N. N. Kovalenok (2004) Synthesis of optimal signals for the control of dynamical systems with Lipschitz bang-bang actuators. Dokl. Akad. Nauk, Ross. Akad. Nauk Gabasov R. , F. M. Kirillova and N. V. Balashevich (2001). Algorithms for open-loop and closed-loop optimization of control systems with intermediate state constraints. Comput. Math. Phys. Information on disturbances is not used Exact measurements of all states are available Mathematical model with lumped parameters, not large Problem is linear Gabasov 12 NATO ARW, October 21 -25

Optimal guaranteeing feedbacks (11) disturbance set of possible values of the disturbance Types of feedback : n q Gabasov unclosable n closed R. Gabasov, F. M. Kirillova and N. V. Balashevich (2004). Guaranteed on-line control for linear systems under disturbances. Functional Differential Equations 13 NATO ARW, October 21 -25

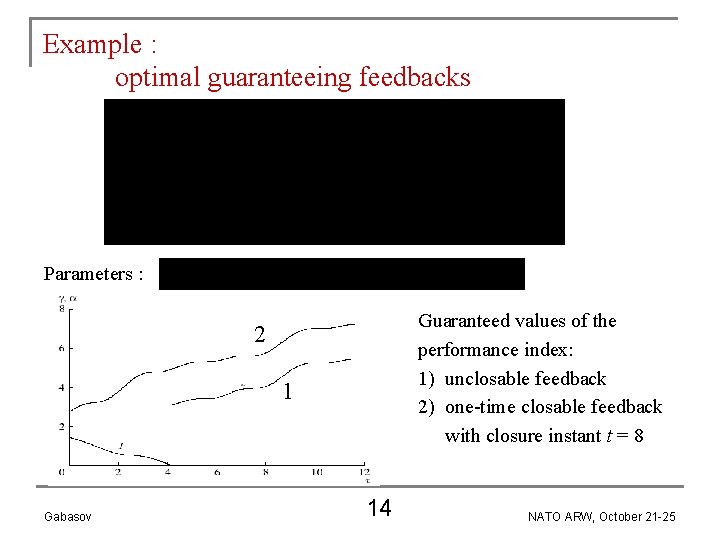
Example : optimal guaranteeing feedbacks Parameters : Guaranteed values of the performance index: 1) unclosable feedback 2) one-time closable feedback with closure instant t = 8 2 1 Gabasov 14 NATO ARW, October 21 -25
![Control System under Disturbances Tt t control interval Dynamical system with disturbance Control System under Disturbances T=[t*, t*] : control interval Dynamical system with disturbance :](https://slidetodoc.com/presentation_image_h2/fbc90baef589b2652ef9655c24c64807/image-15.jpg)
Control System under Disturbances T=[t*, t*] : control interval Dynamical system with disturbance : (12) : piecewise continuous matrix function Measuring device : (13) : continuous matrix function : output : errors of the measuring device Measurements are made at discrete instants Gabasov 15 NATO ARW, October 21 -25

Elements of uncertainty Initial state : (14) : given : set of possible values of parameters z Disturbance : (15) : piecewise continuous functions (L={1, 2, …nv}) : vector of parameters of the disturbance : set of possible values of parameters v Measurement errors : (16) Gabasov 16 NATO ARW, October 21 -25

Classical control of the system under uncertainty t = t* : n n n measurement y(t*) is obtained (generated by x(t*), ξ(t*)) vector u(t*) = u(t*, y(t*)) U is chosen control function u(t) = u(t*), t [t*, t*+h[, is fed into the system t = t*+h : system moves to the state x(t*+h) n measurement y(t*+h) is obtained (generated by x(t*+h), ξ(t*+h)) ……. n t= : n measurement y( ) is obtained signal n vector u( ) = u( , y (·)) U is chosen n n is formed control function u(t) = u( ), t [ , +h[, is fed into the system : totality of all signals y (·) that can be obtained under chosen u Gabasov 17 NATO ARW, October 21 -25

Optimal classical feedback Feedback under inaccurate measurements : (17) : set of all trajectories of (18) for a chosen feedback u and a fixed signal y(·)=(y(t), t Th) Admissible feedback : Performance index : Optimal (guaranteeing) feedback : Gabasov 18 NATO ARW, October 21 -25

Optimal on-line control Suppose that by the moment : n measurements n controls n has been made has been calculated in time (neglected for simplicity) control function has been fed into the system At the moment : n current measurement y*( ) is obtained Aim : n calculate current value of control n feed to the input of control object the control function Gabasov 19 NATO ARW, October 21 -25

A priori and a posteriori distribution sets A priori distribution sets : Z : a priori distribution set of parameters z of the initial state x(t*) V : a priori distribution set of parameters v of the disturbance w(t), t T =Z V=(γ=(z, v) : z Z, v V) : a priori distribution of unknown parameters γ of the system A posteriori distribution set : set of all vectors γ to which there correspond the initial condition x(t*)=x 0+Gz and the disturbance w(t)=Λ(t)v, t [t*, [, able together with some measurement error ξ(t), t Th( ), to generate the signal Gabasov 20 NATO ARW, October 21 -25

Admissible open-loop control (program) Function is said to be an admissible open-loop control if together with it transfers the control system (12) at the moment t* on the terminal set X* for all γ from Equivalent to : The admissible control transfers the determined system (19) : state of this system with x(t*)=x 0, u(t)=u*(t), t [t*, [ at the moment t* to the terminal set: (20) Gabasov 21 NATO ARW, October 21 -25

Accompanying optimal observation problems To establish admissibility of control extremal problems it is required to solve (21) : i-th row of matrix H Problems (21) are called optimal observation problems accompanying the optimal control problem under uncertainty (accompanying optimal observation problems) Gabasov 22 NATO ARW, October 21 -25

Optimal open-loop control and accompanying optimal control problem The quality of the admissible open-loop control is evaluated by Optimal open-loop control solves problem (22) called optimal control problem accompanying the optimal control problem under uncertainty (accompanying optimal control problem) Let Gabasov 23 NATO ARW, October 21 -25

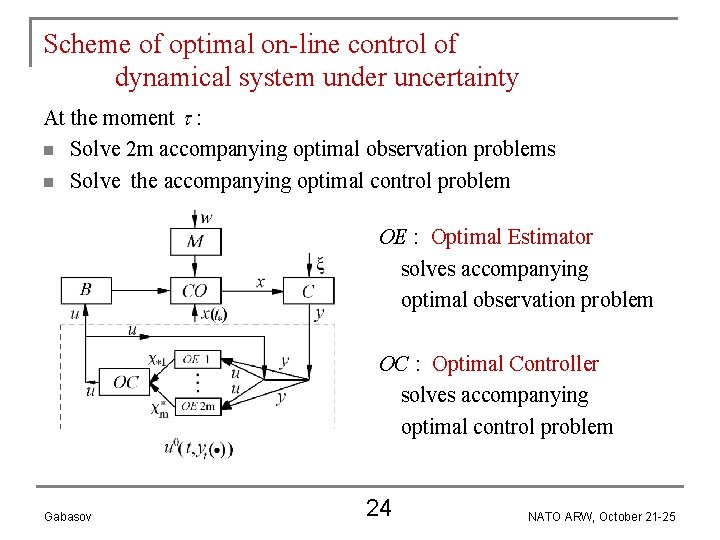
Scheme of optimal on-line control of dynamical system under uncertainty At the moment : n Solve 2 m accompanying optimal observation problems n Solve the accompanying optimal control problem OE : Optimal Estimator solves accompanying optimal observation problem OC : Optimal Controller solves accompanying optimal control problem Gabasov 24 NATO ARW, October 21 -25

Optimal observation problems n Gabasov R. , Dmitruk N. M. , Kirillova F. M. (2002). Optimal Observation of Nonstationary Dynamical Systems. Journal of Computer and Systems Sciences Int. n Gabasov R. , Dmitruk N. M. , Kirillova F. M. (2004). Optimal Control of Multidimensional Systems by Inaccurate Measurements of Their Output Signals. Proceedings of the Steklov Institute of Mathematics. Gabasov 25 NATO ARW, October 21 -25

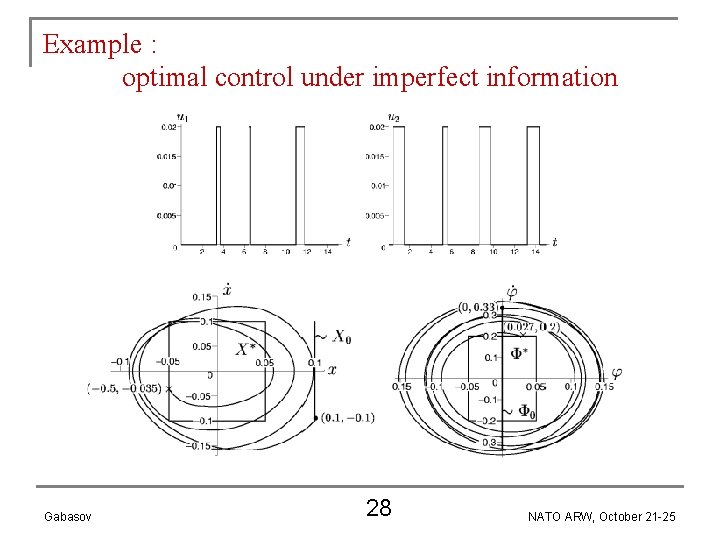
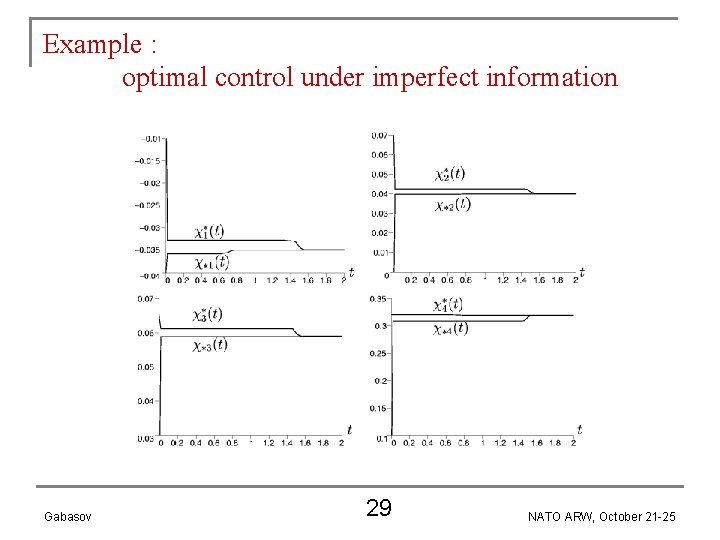
Example : optimal control under imperfect information Mathematical model : Control interval : T=[0, 15] Parameters : Initial condition : Disturbance : Sensor : Gabasov 26 NATO ARW, October 21 -25

Example : optimal control under imperfect information Performance index : Terminal condition : Particular process : Gabasov 27 NATO ARW, October 21 -25

Example : optimal control under imperfect information Gabasov 28 NATO ARW, October 21 -25

Example : optimal control under imperfect information Gabasov 29 NATO ARW, October 21 -25

Optimal decentralized control Optimal control of a group of q objects: Gabasov 30 NATO ARW, October 21 -25

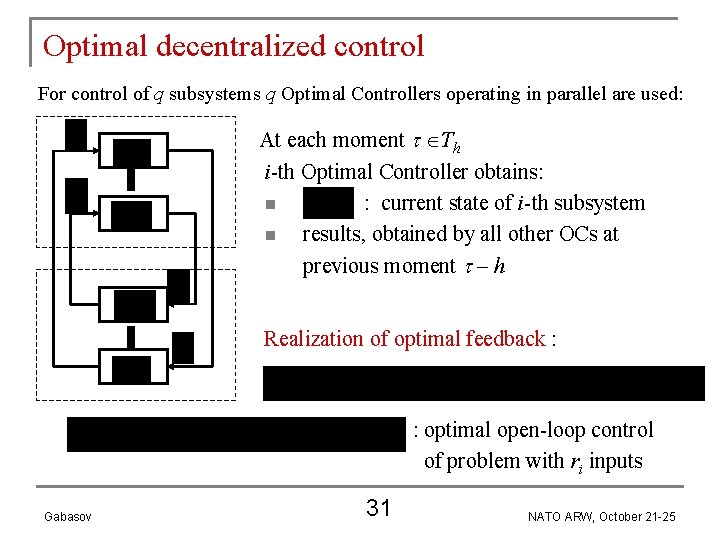
Optimal decentralized control For control of q subsystems q Optimal Controllers operating in parallel are used: At each moment Th i-th Optimal Controller obtains: n : current state of i-th subsystem n results, obtained by all other OCs at previous moment – h Realization of optimal feedback : : optimal open-loop control of problem with ri inputs Gabasov 31 NATO ARW, October 21 -25

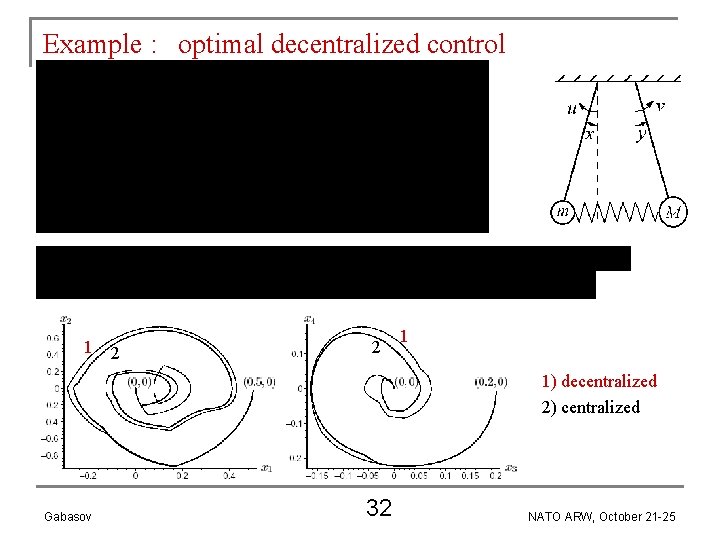
Example : optimal decentralized control 1 2 2 1 1) decentralized 2) centralized Gabasov 32 NATO ARW, October 21 -25

Parallelizing of computations during optimal control of large systems (1) e. g. , two systems : Gabasov 33 NATO ARW, October 21 -25

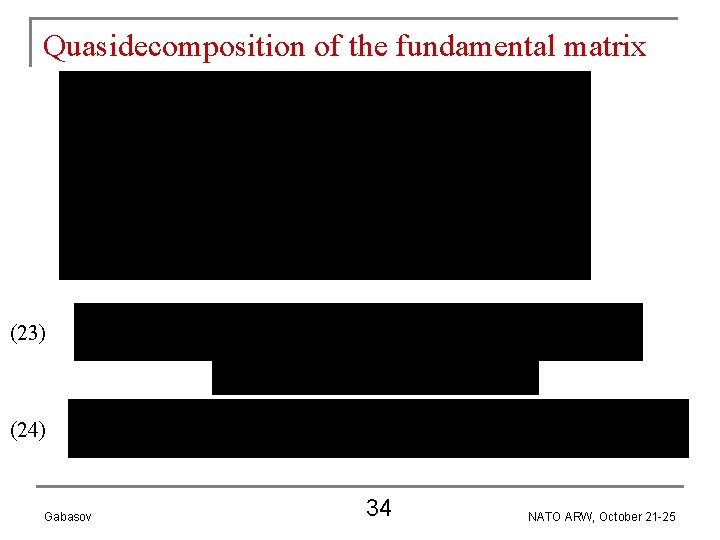
Quasidecomposition of the fundamental matrix (23) (24) Gabasov 34 NATO ARW, October 21 -25

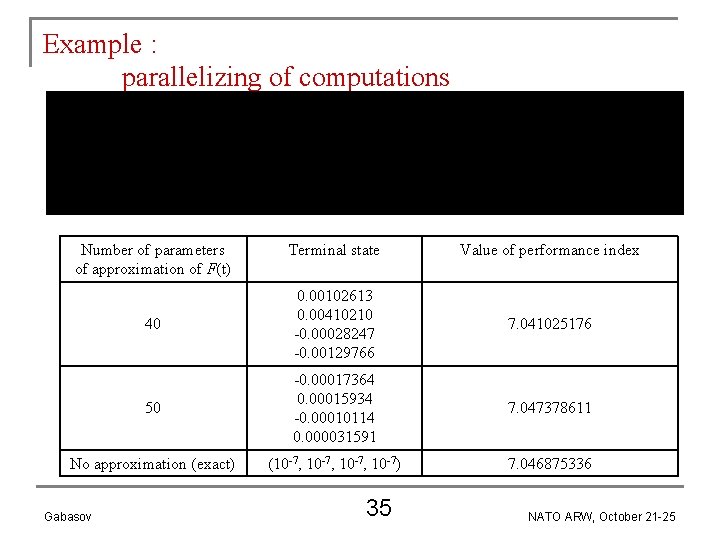
Example : parallelizing of computations Number of parameters of approximation of F(t) Terminal state Value of performance index 40 0. 00102613 0. 00410210 -0. 00028247 -0. 00129766 7. 041025176 50 -0. 00017364 0. 00015934 -0. 00010114 0. 000031591 7. 047378611 No approximation (exact) (10 -7, 10 -7) 7. 046875336 Gabasov 35 NATO ARW, October 21 -25

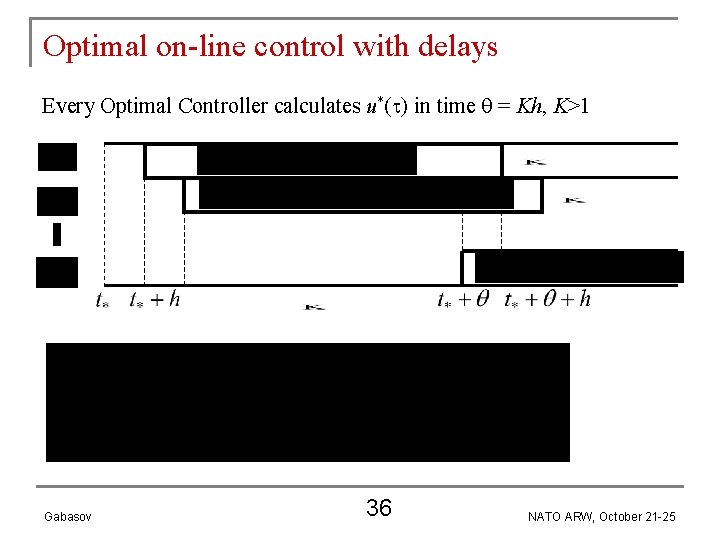
Optimal on-line control with delays Every Optimal Controller calculates u*( ) in time = Kh, K>1 Gabasov 36 NATO ARW, October 21 -25

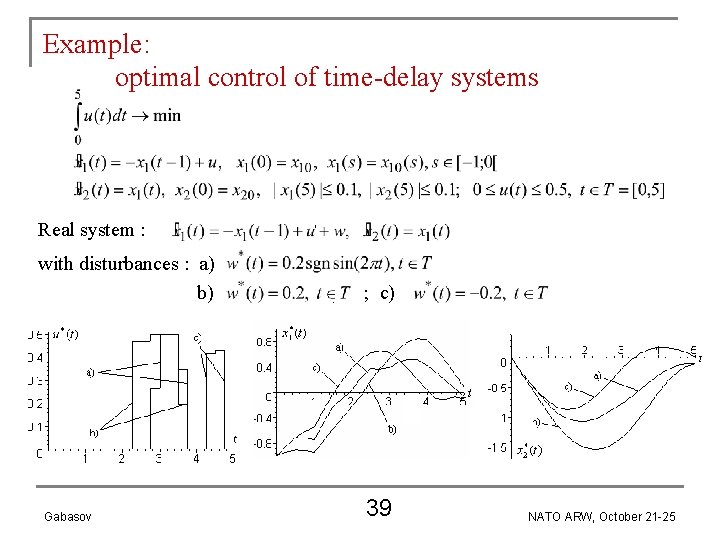
Optimal control of time-delay systems (25) a(t) R, t T; x 10(t) R, t [t*– , t*[ : piecewise continuous functions : delay; e=(1, 0, …, 0) Rn Optimal feedback : : state of system u 0(t| , z (·)), t T( ) : optimal open-loop control of (25) for ( , z (·)) Realization of optimal feedback : Gabasov 37 NATO ARW, October 21 -25

Quasireduction of the fundamental matrix pi 1(t), t T : finite-parametric approximations of fi 1(t), t T , φij(t), t T : solutions to n – 1 systems of ODE’s R. Gabasov, O. Yarmosh. Fast algorithm of open-loop solution in a linear optimal control problem for dynamical systems with delays. Today, Section C-1. Gabasov 38 NATO ARW, October 21 -25

Example: optimal control of time-delay systems Real system : with disturbances : a) b) Gabasov , . ; c) 39 NATO ARW, October 21 -25

Optimal control of PDEs Problem of optimal heating (26) x(s, t), (s, t) Q : temperature at point s at instant t u(t), t T : control a, ν , α, β>0 : given constants; h(s) Rm, s S; g*, g* Rm Gabasov 40 NATO ARW, October 21 -25

Approximation of PDE Sη={0, η, …, l- η, l}, l/K, K>0 ys(t)=x(s, t), s Sη, t T (27) y 0=(x 0(s), s Sη), H =(h(s), s Sη), b=(0, 0, …, 0, aν/η) Gabasov 41 NATO ARW, October 21 -25

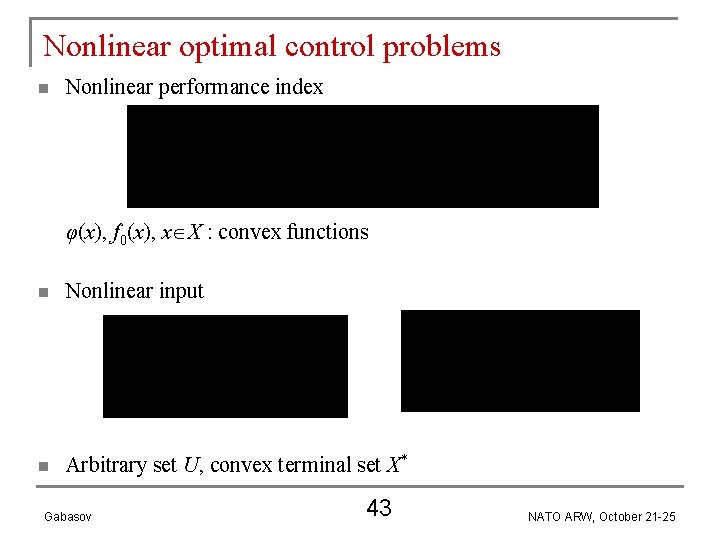
Nonlinear optimal control problems n Nonlinear dynamics f(x), x X : q Gabasov N. V. Balashevich, R. Gabasov, A. I. Kalinin, and F. M. Kirillova (2002). Optimal Control of Nonlinear Systems. Comp. Mathematics and Math. Physics 42 NATO ARW, October 21 -25

Nonlinear optimal control problems n Nonlinear performance index φ(x), f 0(x), x X : convex functions n Nonlinear input n Arbitrary set U, convex terminal set X* Gabasov 43 NATO ARW, October 21 -25

Stabilization of dynamical systems n Gabasov R. Kirillova F. M. and O. I. Kostyukova (1995). Dynamic system stabilization methods. Journal of Computer and Systems Sciences International. n Gabasov, R. F. ; Ruzhitskaya, E. A. (1999). A method of stabilization of dynamic systems under persistent perturbations. Cybernetics and Systems Analysis Gabasov 44 NATO ARW, October 21 -25
 Constructive proof vs non constructive
Constructive proof vs non constructive Constructive proof vs non constructive
Constructive proof vs non constructive Constructive proof vs non constructive
Constructive proof vs non constructive Rules of inference
Rules of inference Symbolic reasoning under uncertainty
Symbolic reasoning under uncertainty Uncertainity in decision making
Uncertainity in decision making Decision-making under uncertainty
Decision-making under uncertainty Capital budgeting under risk and uncertainty
Capital budgeting under risk and uncertainty Expected profit under uncertainty
Expected profit under uncertainty Optimal control lqr
Optimal control lqr Indirect methods of contoring uses how many methods
Indirect methods of contoring uses how many methods Methods to control water pollution
Methods to control water pollution Media access control methods
Media access control methods Methods of portion control in bread and pastry
Methods of portion control in bread and pastry Methods of establishing control points in surveying
Methods of establishing control points in surveying Quality control methods for medicinal plant materials
Quality control methods for medicinal plant materials Chemical engineering nmsu
Chemical engineering nmsu Time stamping in database
Time stamping in database Methods of establishing control points in surveying
Methods of establishing control points in surveying Air pollution control methods
Air pollution control methods Data entry quality control
Data entry quality control Explain the credit control measures of rbi
Explain the credit control measures of rbi On optimistic methods for concurrency control
On optimistic methods for concurrency control Control of noise pollution ppt
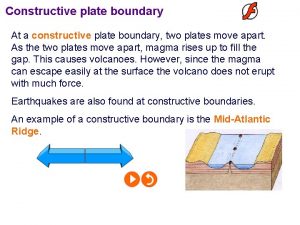
Control of noise pollution ppt Differences between constructive and destructive waves
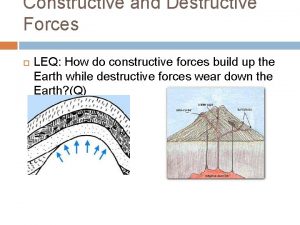
Differences between constructive and destructive waves Constructive interference
Constructive interference Constructive speech
Constructive speech Constructive cost model
Constructive cost model Constructive cost model
Constructive cost model Tectonic plate movement
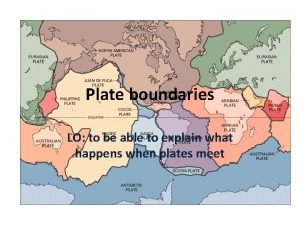
Tectonic plate movement Constructive alignment
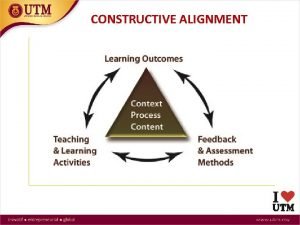
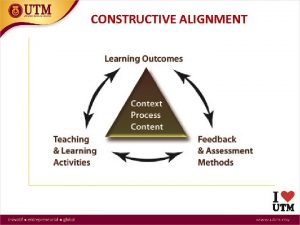
Constructive alignment Constructive and destructive conflict
Constructive and destructive conflict Destructive processes
Destructive processes Constructive possession
Constructive possession Michelson interferometer formula
Michelson interferometer formula Constructive eviction indiana
Constructive eviction indiana Progress checker
Progress checker Constructive alignment of the components of a lesson plan
Constructive alignment of the components of a lesson plan Litmos medstar
Litmos medstar Constructive feedback examples
Constructive feedback examples Dichotomy corollary
Dichotomy corollary Destructive communication
Destructive communication Sublimation vs displacement
Sublimation vs displacement Constructive criticism vs destructive criticism
Constructive criticism vs destructive criticism Conflict with others
Conflict with others