Conditions for Distortionless Transmission n Transmission is said

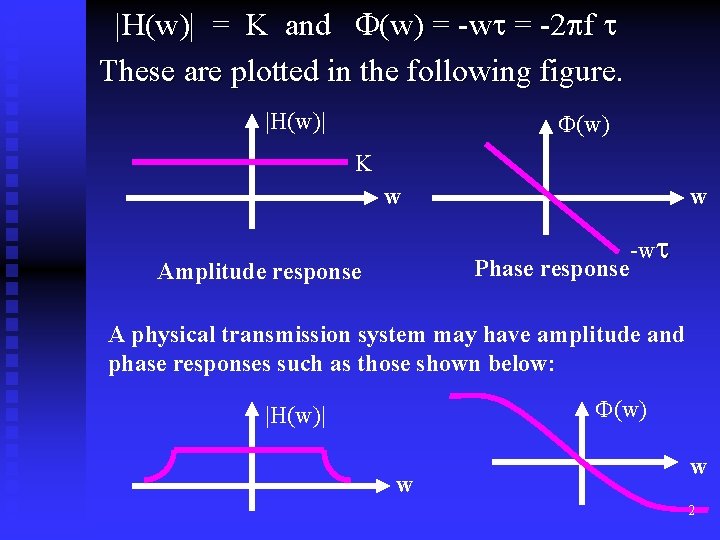
Conditions for Distortionless Transmission n Transmission is said to be distortion less if the input and output have identical wave shapes within a multiplicative constant. A delayed output that retains the input waveform is also considered distortion less. Thus in distortion-less transmission, the input x(t) and output y(t) satisfy the condition: y(t) = Kx(t - ) (1) where is the delay time and k is a constant. Computing the Fourier Transform of (1) we obtain Y(w) = KX(w)e-jw (2) The magnitude and phase response of (2) is 1 given by

|H(w)| = K and (w) = -w = -2 f These are plotted in the following figure. |H(w)| (w) K w w Phase response Amplitude response -w A physical transmission system may have amplitude and phase responses such as those shown below: (w) |H(w)| w w 2

Ideal Filters Filter: A very general term denoting any system whose output is a specified function of its input. Frequency Selective Filters: Low-Pass, High-Pass, Band-Stop. Ideal Low-Pass Filter: An ideal low-pass filter passes all Signal components having frequency less than ww radian per second with no distortion and completely attenuates signal components having frequencies greater than wc Hz. |H(w)| -wc (w) wc w w 3

Ideal High-Pass Filter: An ideal High-Pass filter passes all signal components greater than ww radian per second with no distortion and completely attenuates signal components having frequencies less than ww radian per second. |H(w)| -wc wc w (w) w 4

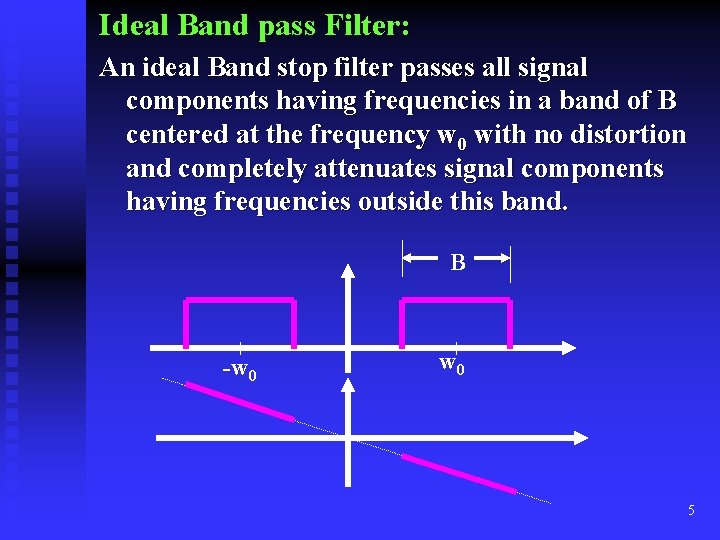
Ideal Band pass Filter: An ideal Band stop filter passes all signal components having frequencies in a band of B centered at the frequency w 0 with no distortion and completely attenuates signal components having frequencies outside this band. B -w 0 5

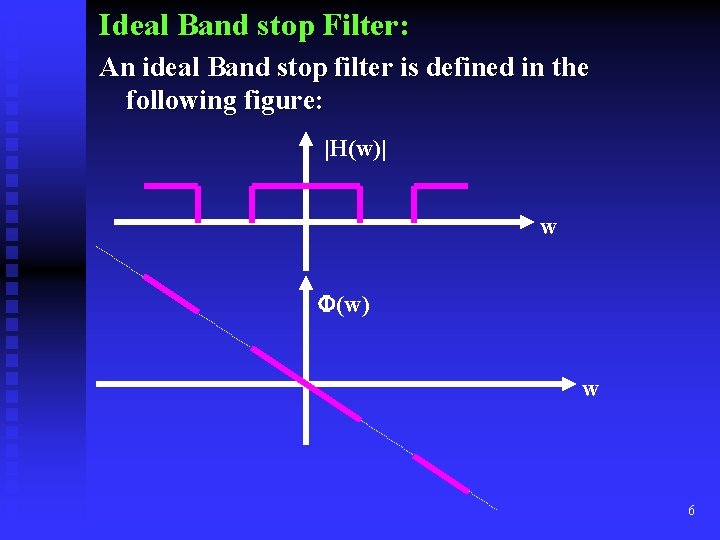
Ideal Band stop Filter: An ideal Band stop filter is defined in the following figure: |H(w)| w (w) w 6

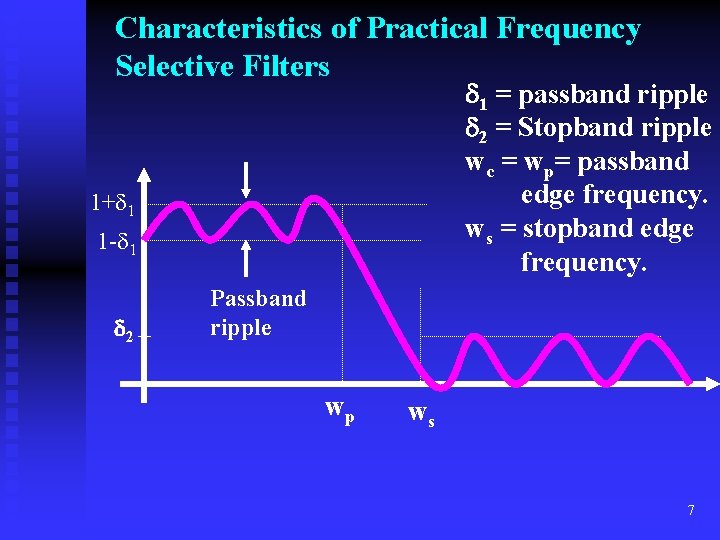
Characteristics of Practical Frequency Selective Filters 1 = passband ripple 2 = Stopband ripple wc = wp= passband edge frequency. ws = stopband edge frequency. 1+ 1 1 - 1 2 Passband ripple wp ws 7

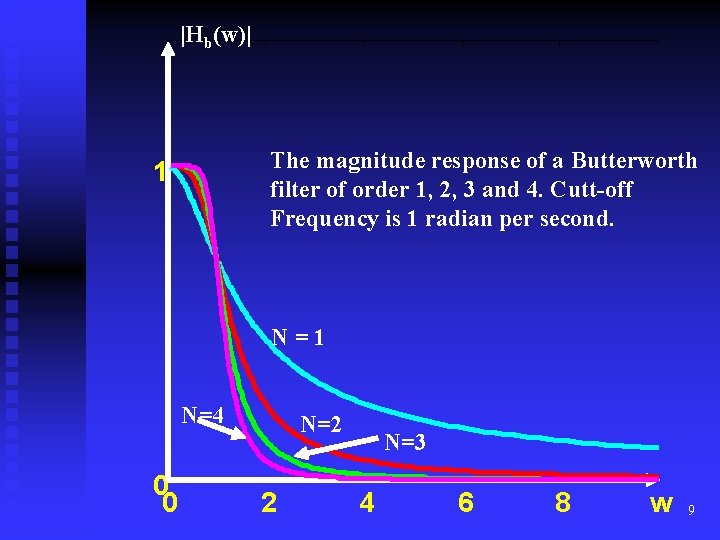
Analogue Filters: The Low-Pass Butterworth Approximation: A Low-pass Butterworth filter has the amplitude response n (1) where n 1 is the filter order and the subscript b denotes the Butterworth filter. wc is the cutt-off frequency of the filter. It is obvious from equation (1) that the Butterworth filter is an all Pole filter (i. e. N poles but no zeros). 8

|Hb(w)| The magnitude response of a Butterworth filter of order 1, 2, 3 and 4. Cutt-off Frequency is 1 radian per second. 1 N=4 0 0 N=2 2 N=3 4 6 8 w 9

The poles of a Butterworth filter can be computed as follows: From (1) or The poles of the filter are the roots of the denominator, i. e. or or k = 0, 1, 2, …. , N-1 (2) 10

Example 1: Derive the transfer function of a first-order Butterworth filter. The cutoff frequency is 1 radian per second. Solution: The poles of a first-order Butterworth n filter can be computed by putting k=0 and N = 1 in equation (2). i. e. s 0 = wcej /2 = ej (wc = 1) = cos + jsin = -1 + 0 = -1 This means that the transfer function of the filter is 11

Example 2: Repeat example 1 for a second order Butterworth filter. Solution: The poles of a second-order n Butterworth filter can be computed by putting k=0, 1 and N = 2 in equation (2). i. e. s 0 = wcej /2 ej /4 = ej 3 /4 (wc = 1) = cos(3 /4) + jsin(3 /4) = -1/ 2 + j 1/ 2 and s 1 = ej /2 ej 3 /4 = ej 5 /4 = -1/ 2 - j 1/ 2 This means that the transfer function of the filter is Tutorial: Repeat example 2 for a 3 rd and 4 th order Butterworth filter. 12

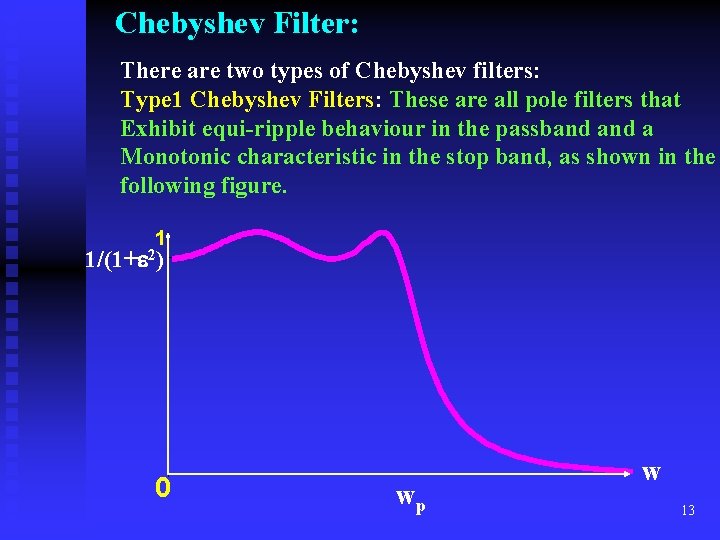
Chebyshev Filter: There are two types of Chebyshev filters: Type 1 Chebyshev Filters: These are all pole filters that Exhibit equi-ripple behaviour in the passband a Monotonic characteristic in the stop band, as shown in the following figure. 1 1/(1+ 2) 0 wp w 13

Type 2 Chebyshev Filter: These filters contain both poles and zeros and exhibit a monotonic behaviour in the passband an equiripple behaviour in the stopband. The magnitude response of a typical low-pass type 2 chebyshev filter is shown in the following figure. 1 00 2 4 6 8 1014

The magnitude of the frequency response characteristics of a type 1 Chebyshev filter is given by where is a parameter of the filter that is related to the ripple in the pass-band TN(x) is the Nth order Chebyshev polynomial defined as The Chebyshev polynomials can be generated by the recursive equation TN+1(x) = 2 x. TN(x) – TN-1(x), N = 1, 2, … (3) where T 0(x) = 1 and T 1(x) = x. From (3) T 2(x) = 2 x 2 – 1, T 3(x) = 4 x 3 – 3 x, and so on. 15

The filter parameter is related to the ripple in the passband, as shown in the figure of the previous slide. A relationship between passband ripple 1 and the parameter is given by 1 = 10 log(1 + 2) or = (10 1/10 – 1) Example 3: Derive transfer function of a first-order Cheby. Shev filter of type 1 with a unity gain and a passband ripple of 2 d. B. Solution: = (102/10 – 1) = 0. 7648, T 12 = (w/wc)2 16

Therefore, Example 4: Find the transfer function for a second order normalized (wc = 1) Chebyshev low-pass filter with unity maximum gain and 1. 5 d. B of ripple in the passband. Solution: 1 = 1. 5 d. B, wc = 1, 2 = 101. 5/10 – 1 = 0. 4125 17

Tutorial Q 2: Derive the transfer function of a second order Low-pass chebyshev filter with unity dc gain and a passband Ripple of 2 d. B. 18