Computational Fluid Dynamics Lecture II Numerical Methods and

Computational Fluid Dynamics Lecture II Numerical Methods and Criteria for CFD Dr. Ugur GUVEN Professor of Aerospace Engineering

Mathematical Solutions • Most non linear differential equations have no solution and you have to use numerical approximations • You will have to transform the differential equations using discretization methods to algebraic equations in order to make it solvable • You Will have to use some software such as Mathlab, Mathematica or a FORTRAN program to solve these algebraic equations. • You will have to use many iterations to make sure that you approximate the correct solution

Discretization • The process of converting differential equations into algebraic equations is called discretization. • Discretization is necessary for numerical methods and computational programming to be employed in solving fluid dynamics equations • Of course, improper discretization may cause errors in calculation

Discretization Methods • Make sure that you choose the correct discretization methods for solving partial differential equations. These include: 1) Finite Difference Methods 2) Finite Volume Methods 3) Finite Elements Methods

Discretization Methods • These methods can be summarized as: • A) Finite Difference Methods are used especially for easy geometries and for simple flow problem equations. • B) Finite Volume Methods are more applicable to a wide variety of flow problems and wide variety of geometries • C) Finite Elements Method is more flexible, but it is more suitable for solid structures.

Finite Differences Methods • Finite Differences Methods are used to turn differential equations into algebraic equations by transforming derivatives into limited terms using Taylor’s series. • For simple differential equations with first to nth degree derivatives, you can use finite differences to create algebraic equations of any equation that contains partial derivatives.

Finite Volume Methods • In the finite volume methods, you concentrate on the geometry of the solution domain and on the geometry of the boundary values. • Hence, the equations are solved on the integral level by limiting the geometric domains.

Finite Elements Method • In the finite elements method, the physical model is deconstructed into infinitesimal parts that accurately model the overall system. • Then, the solution is carried out for that small element and the solution is extrapolated for the whole system. • Finite Elements are more suitable for systems with solid objects.

Grid Types for Numerical Methods Block Structured Grid

Grid Types for Numerical Methods Composite (Chimera) Grid Unstructured Grid

Meshing • Meshing is the concept of adjusting the grid to cover as many points as possible, in order to increase the accuracy without creating complex calculations. • Each cell is calculated separately and then all cells are superimposed to create one big solution.

Properties of the Solution Method • • Consistency Stability Convergence Conservation Boundedness Realizability Accuracy

Consistency

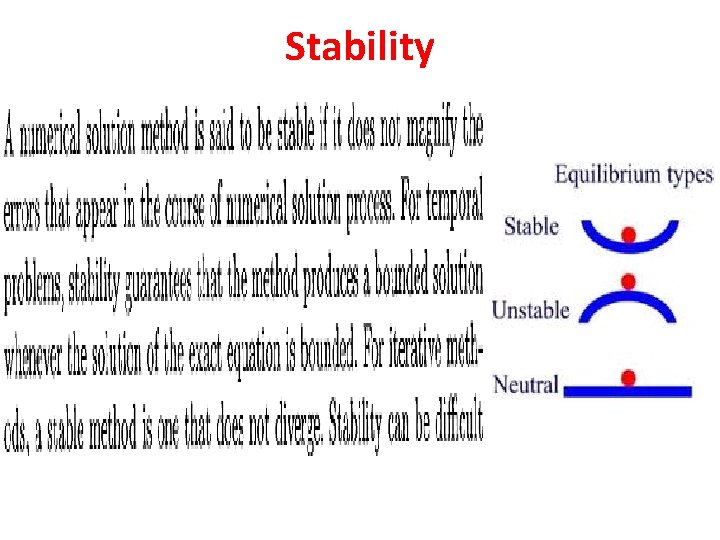
Stability

Convergence

Conservation

Boundedness

Realizability Divergence

Accuracy • It is to be remembered that the final solution is only an approximation of the real differential equations. • Hence, there may be accuracy issues due to the amount of errors in the approximation process • It is important for accuracy to be within acceptable boundaries

Errors in the Numerical Solution • Various errors can be introduced into the solution during the course of the development of the solution algorithm as well as in the programming stage or in setting up of the boundary conditions

Error Control in Numerical Solutions

Thank You www. cfdlectures. co. cc drguven@live. com