Composites Design and Analysis StressStrain Relationship Prof Zaffar

Composites Design and Analysis Stress-Strain Relationship Prof Zaffar M. Khan Institute of Space Technology Islamabad

Next Generation Aerospace Vehicle Requirements 2

Composite design and analysis

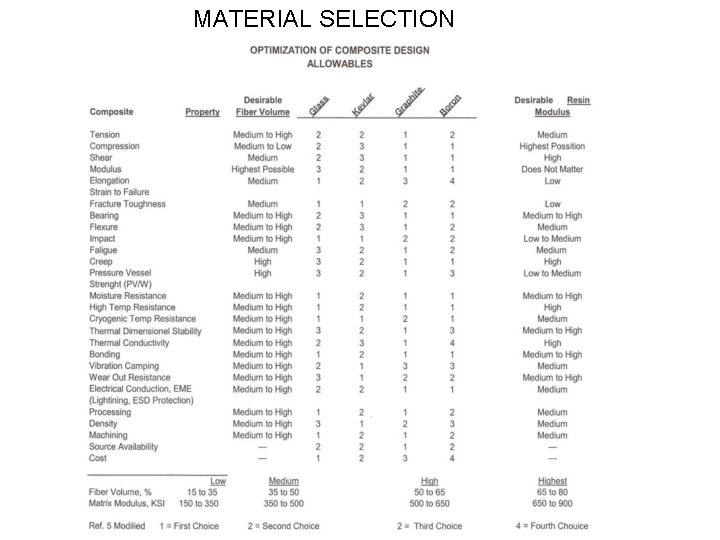
MATERIAL SELECTION 4

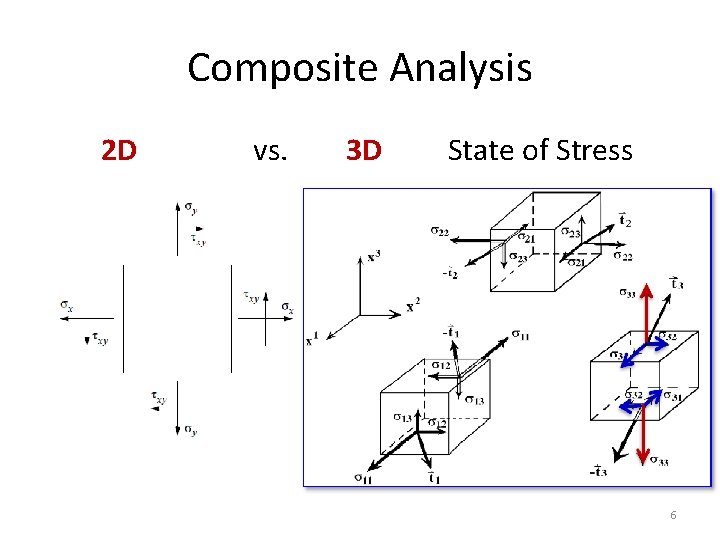
Composite Analysis 2 D vs. 3 D State of Stress 6

Required elastic material properties for composites • Metals (isotropic materials) – E, G, ν – 2 independent properties – G = __E____ 2(1 + ν) • Composite lamina (unidirectional layer, ply) – In plane: E 1, E 2, G 12, ν 12 – Out of plane : E 3, G 13, G 23, ν 13, ν 23 • But for transverse isotropy (2 = 3): E 2 = E 3 G 12 = G 13 ν 12 = ν 13 G 23 = __E 23___ 2(1 + ν 23) Therefore 5 independent properties: E 1 E 2 G 12 ν 12 G 23

Terminology used in micromechanics • • • Ef, Em - Young’s modulus of fiber and matrix Gf, Gm - Shear modulus of fiber and matrix νf, νm - Poisson’s ratio of fiber and matrix Vf, Vm - Volume fraction of fiber and matrix Wf, Wm – Weight fraction of fiber and matrix

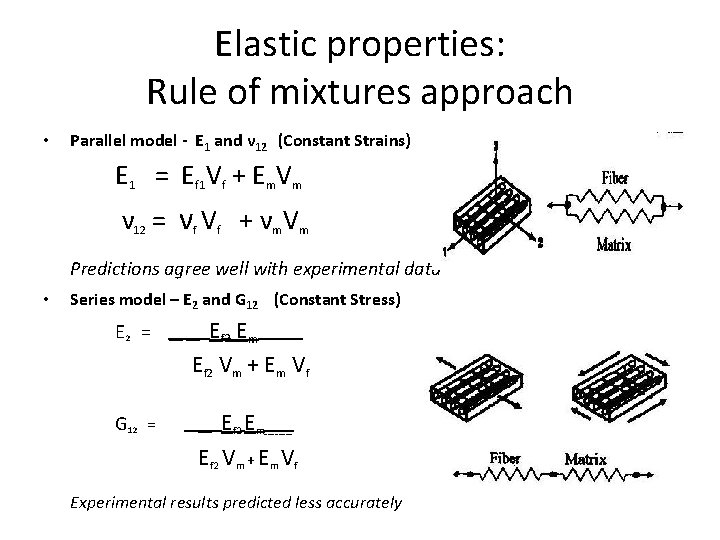
Elastic properties: Rule of mixtures approach • Parallel model - E 1 and ν 12 (Constant Strains) E 1 = Ef 1 Vf + Em. Vm ν 12 = νf Vf + νm. Vm Predictions agree well with experimental data • Series model – E 2 and G 12 (Constant Stress) E 2 = __ __ Ef 2 Em____ Ef 2 Vm + Em Vf G 12 = __ __ Ef 2 Em ____ Ef 2 Vm + Em Vf Experimental results predicted less accurately

Micromechanics example: Volume fraction changes Knowns : Carbon: E = 34. 0 x 106 psi Epoxy : E = 0. 60 x 106 psi • How much does the longitudinal modulus change when the fiber volume fraction is changed from 58% to 65%? E 1 = Ef 1 Vf + Em Vm - For Vf = 0. 58: E 1 = (34. 0 x 106 psi)(. 58) + (0. 60 x 106 psi)(0. 42) = 20. 0 x 106 psi - For Vf = 0. 65: E 1 = (34. 0 x 106 psi)(. 65) + (0. 60 x 106 psi)(0. 35) = 22. 3 x 106 psi Thus, raising the fiber volume fraction from 58% to 65% increases E 1 by 12%

Design and analysis of composite laminates: Laminated Plate Theory (LPT) • Used to determine the response of a composite laminate based on properties of a layer (or ply)

Laminate Ply Orientation Code Designate each ply by it’s fiber orientation angle List plies in sequence starting from top of laminate Adjacent plies are separated by “/” if their angle is different Designate groups of plies with same angle using subscripts Enclose complete laminate in brackets Use subscript “S” to denote mid plane symmetry, or “T” to denote total laminate • Bar on the top of the ply indicates mid-plane • • •

Special types of laminates • Symmetric laminate – for every ply above the laminate mid plane, there is an identical ply(material and orientation) an equal distance below the mid plane • Balanced laminate – for every ply at a +θ orientation, there is another ply at the – θ orientation somewhere in the laminate • Cross-ply laminate – composed of plies of either 0 o or 90 o (no other ply orientations) • Quasi-isotropic laminate – produced using at least three different ply orientations, all with equal angles between them. Exhibits isotropic extensional stiffness properties (have the same E in all in-plane directions)

The response of special laminates • • • Balanced, unsymmetric, laminate – Tensile loading produces twisting curvature – Ex: [+θ/0/- θ]τ Symmetric, unbalanced laminate – Tensile loading produces in-plane shearing – Ex: [+θ/0/- θ]τ Unsymmetric cross-ply laminate – Tensile loading produces bending curvature – Ex: [0/90]τ • Balanced and symmetric laminate – Tensile loading produces extension – Ex: [+θ/- θ]s • Quasi isotropic laminate: [+60/0/- 60]s and [+45/0/+45/90]s – Tensile loading produces extension loading, independent of angle

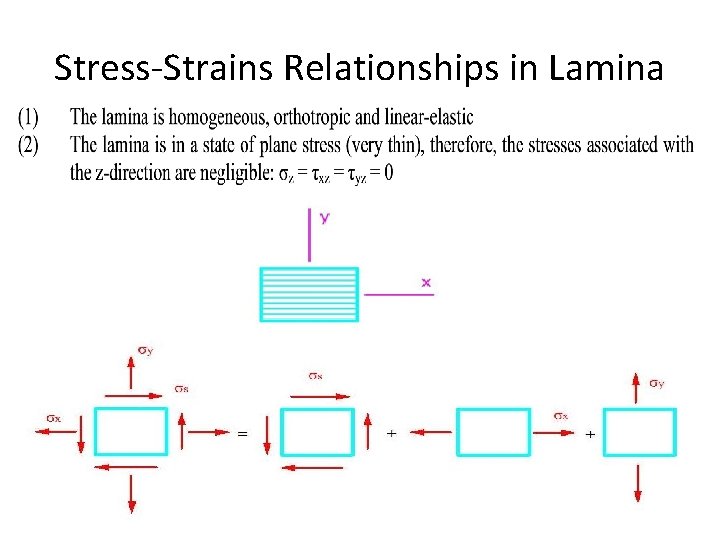
Stress-Strains Relationships in Lamina

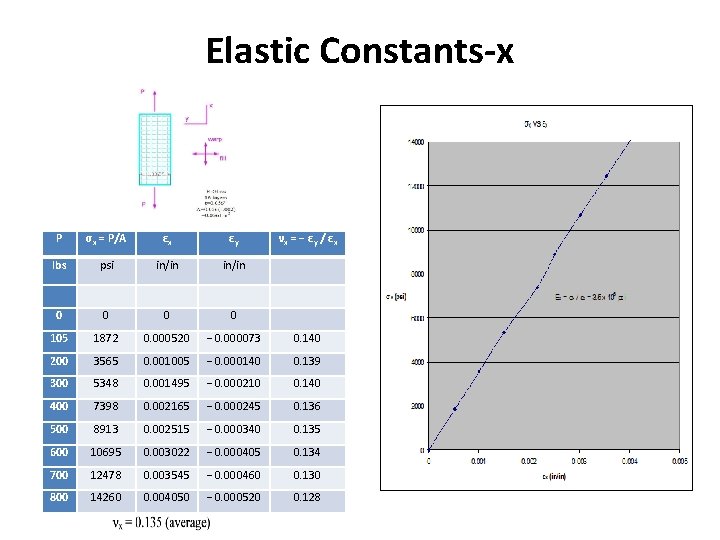
Elastic Constants-x P σx = P/A εx εy νx = − εy / εx lbs psi in/in 0 0 105 1872 0. 000520 − 0. 000073 0. 140 200 3565 0. 001005 − 0. 000140 0. 139 300 5348 0. 001495 − 0. 000210 0. 140 400 7398 0. 002165 − 0. 000245 0. 136 500 8913 0. 002515 − 0. 000340 0. 135 600 10695 0. 003022 − 0. 000405 0. 134 700 12478 0. 003545 − 0. 000460 0. 130 800 14260 0. 004050 − 0. 000520 0. 128

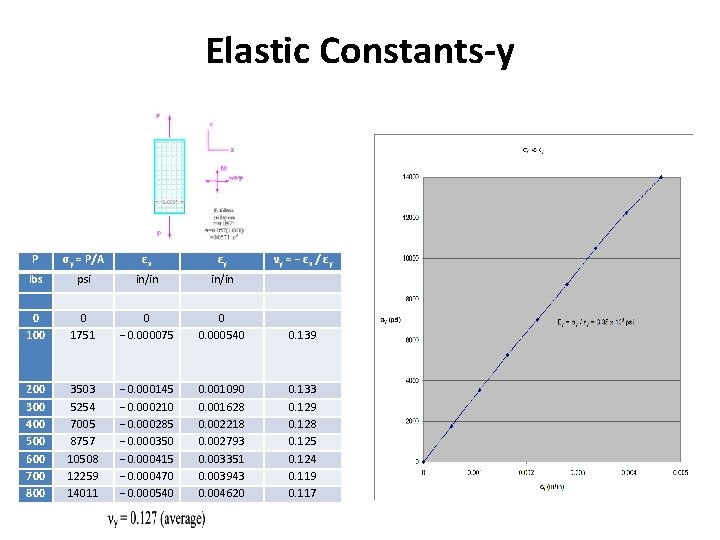
Elastic Constants-y P σy = P/A εx εy νy = − εx / εy lbs psi in/in 0 100 0 1751 0 − 0. 000075 0 0. 000540 200 300 400 500 600 700 800 3503 5254 7005 8757 10508 12259 14011 − 0. 000145 − 0. 000210 − 0. 000285 − 0. 000350 − 0. 000415 − 0. 000470 − 0. 000540 0. 001090 0. 001628 0. 002218 0. 002793 0. 003351 0. 003943 0. 004620 0. 139 0. 133 0. 129 0. 128 0. 125 0. 124 0. 119 0. 117

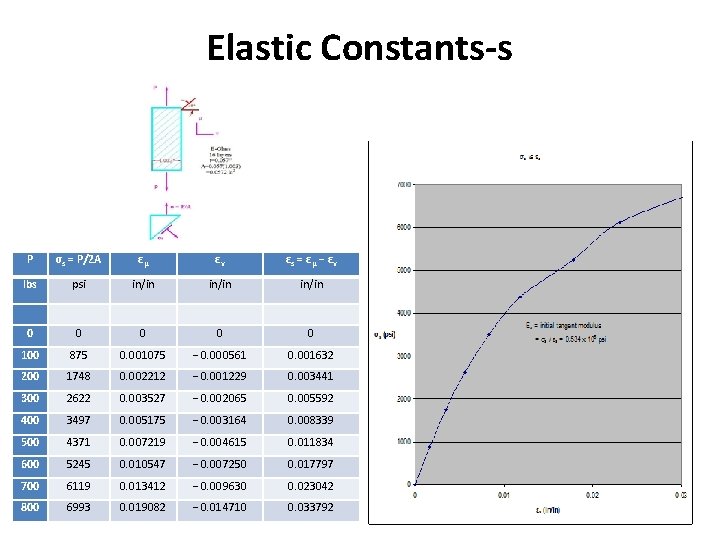
Elastic Constants-s P σs = P/2 A εμ εν εs = εμ − εν lbs psi in/in 0 0 0 100 875 0. 001075 − 0. 000561 0. 001632 200 1748 0. 002212 − 0. 001229 0. 003441 300 2622 0. 003527 − 0. 002065 0. 005592 400 3497 0. 005175 − 0. 003164 0. 008339 500 4371 0. 007219 − 0. 004615 0. 011834 600 5245 0. 010547 − 0. 007250 0. 017797 700 6119 0. 013412 − 0. 009630 0. 023042 800 6993 0. 019082 − 0. 014710 0. 033792

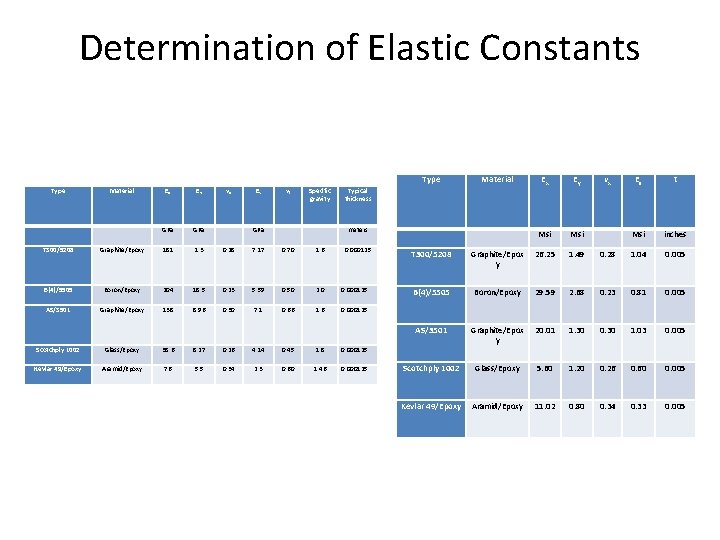
Determination of Elastic Constants Type Material Ex Ey νx Es t meters Msi Msi inches 0. 000125 T 300/5208 Graphite/Epox y 26. 25 1. 49 0. 28 1. 04 0. 005 B(4)/5505 Boron/Epoxy 29. 59 2. 68 0. 23 0. 81 0. 005 AS/3501 Graphite/Epox y 20. 01 1. 30 0. 30 1. 03 0. 005 Scotchply 1002 Glass/Epoxy 5. 60 1. 20 0. 26 0. 60 0. 005 Kevlar 49/Epoxy Aramid/Epoxy 11. 02 0. 80 0. 34 0. 33 0. 005 Type Material Ex Ey νx Es νf Specific gravity Typical thickness GPa GPa T 300/5208 Graphite/Epoxy 181 1. 3 0. 28 7. 17 0. 70 1. 6 B(4)/5505 Boron/Epoxy 204 18. 5 0. 23 5. 59 0. 50 2. 0 0. 000125 AS/3501 Graphite/Epoxy 138 8. 96 0. 30 7. 1 0. 66 1. 6 0. 000125 Scotchply 1002 Glass/Epoxy 38. 6 8. 27 0. 26 4. 14 0. 45 1. 8 0. 000125 Kevlar 49/Epoxy Aramid/Epoxy 76 5. 5 0. 34 2. 3 0. 60 1. 46 0. 000125

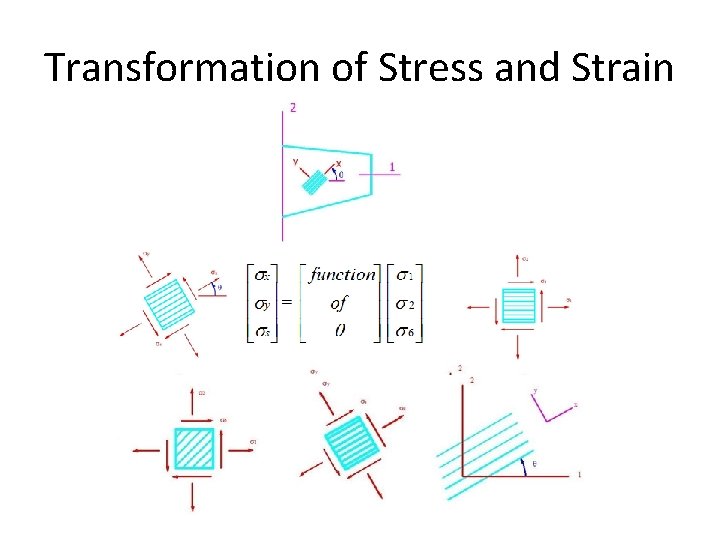
Transformation of Stress and Strain

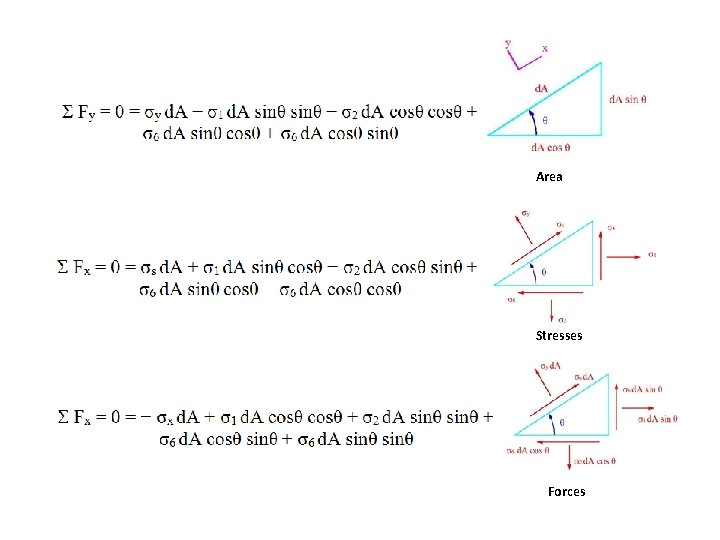
Area Stresses Forces

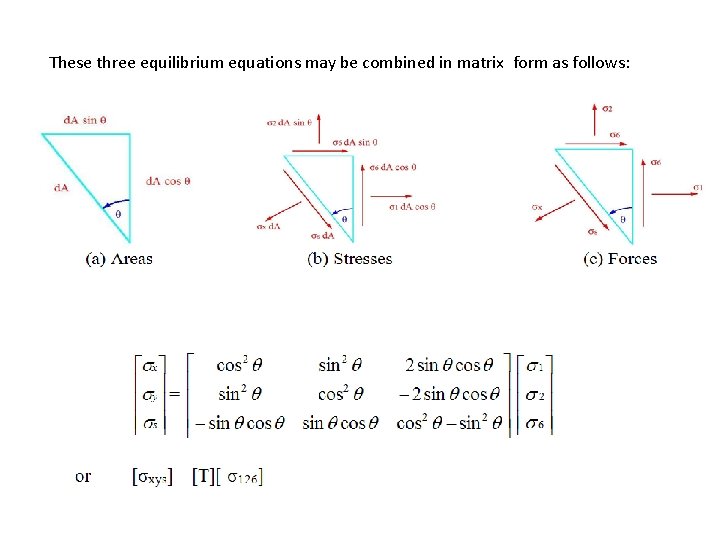
These three equilibrium equations may be combined in matrix form as follows:

The equations for the transformation of strain are the same as those for the transformation of stress:

Stress-Strain Relationships in Global Coordinates Develop the relationship between the stresses and strains in global coordinates. [σxys] = [Qxys] [εxys] [σxys] = [T] [ σ126] [εxys] = [Ť] [ε 126] Substitution of Equations (2) and (3) into (1) yields [T] [ σ126] = [Qxys] [Ť] [ε 126] (3) (1) (2) (4) Pre multiplying both sides of Equation (4) by [T] − 1: [T] − 1 [T] [σ126] = [T] − 1 [Qxys] [Ť] [ε 126] or [ σ126] = [T] − 1 [Qxys] [Ť] [ε 126] (5) (6) or (7) = [T] − 1 [Qxys] [Ť]

or = [Q 126] or [ σ126] = [Q 126] [ε 126] where [Q 126] = [T] − 1 [Qxys] [Ť] Note that [T(+θ)] − 1 = [T(−θ)] The elements of the matrix [Q 126] are as follows: Q 11 = Qxx cos 4θ + 2 (Qxy + 2 Qss) sin 2θ cos 2θ + Qyy sin 4θ Q 22 = Qxx sin 4θ + 2 (Qxy + 2 Qss) sin 2θ cos 2θ + Qyy cos 4θ Q 12 = Q 21 = (Qxx + Qyy − 4 Qss) sin 2θ cos 2θ + Qxy (sin 4θ +cos 4θ) Q 66 = (Qxx + Qyy − 2 Qxy − 2 Qss) sin 2θ cos 2θ + Qss (sin 4θ +cos 4θ) Q 16 = Q 61 = (Qxx – Qxy − 2 Qss) sinθ cos 3θ + (Qxy – Qyy + 2 Qss) sin 3θ co Q 26 = Q 62 = (Qxx – Qxy − 2 Qss) sin 3θ cosθ + (Qxy – Qyy + 2 Qss) sinθcos 3θ

[Q 126] − 1 [ σ126] = [Q 126] − 1 [Q 126] [ε 126] or [Q 126] − 1 [ σ126] = [ε 126] or [ε 126] = [Q 126] − 1 [ σ126] or [ε 126] = [S 126] [ σ126] or The elements of the matrix [S 126] are as follows: S 11 = (Q 22 Q 66 – Q 262) / ∆ S 12 = S 21 = (Q 16 Q 26 – Q 12 Q 66) / ∆ S 16 = S 61 = (Q 12 Q 26 – Q 22 Q 16) / ∆ S 22 = (Q 11 Q 66 – Q 162) / ∆ S 26 = S 62 = (Q 12 Q 16 – Q 11 Q 26) / ∆ S 66 = (Q 11 Q 22 – Q 122) / ∆ where ∆ = Q 11 Q 22 Q 66 + 2 Q 12 Q 26 Q 61 − Q 22 Q 162 – Q 66 Q 122 – Q 11 Q 622

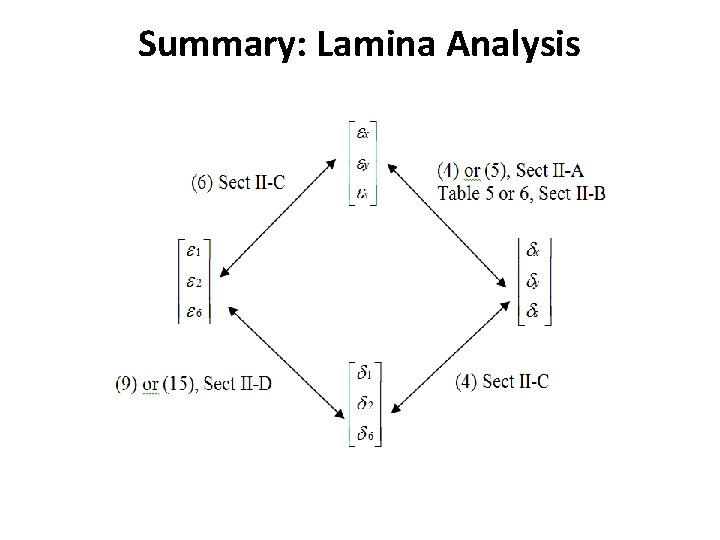
Summary: Lamina Analysis

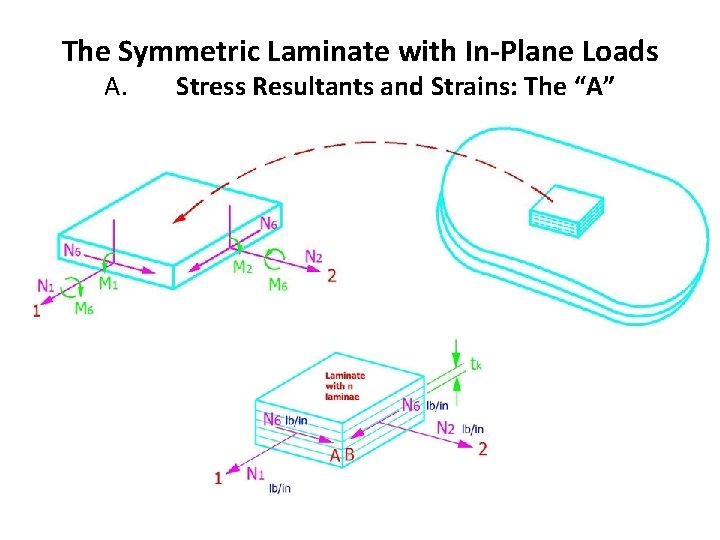
The Symmetric Laminate with In-Plane Loads A. Stress Resultants and Strains: The “A”

Relationship between strains and the stress resultants. Related by constants Aij Deriving expressions for these constants: Expression for is:

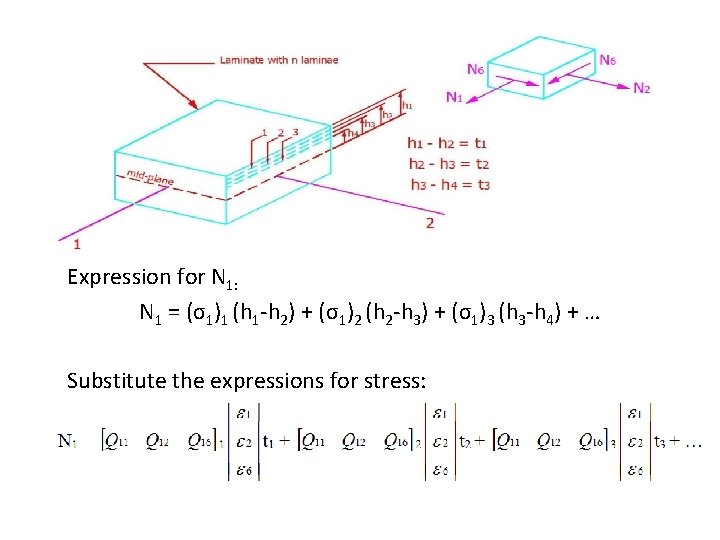
Expression for N 1: N 1 = (σ1)1 (h 1 -h 2) + (σ1)2 (h 2 -h 3) + (σ1)3 (h 3 -h 4) + … Substitute the expressions for stress:

Above equation can be rewritten as: Similarly for N 2 and N 6:

Above can be combined into matrix form as: Or Where A 11 = (Q 11)k tk A 12 = (Q 12)k tk A 16 = (Q 16)k tk A 22 = (Q 22)k tk A 26 = (Q 26)k tk A 66 = (Q 66)k tk

Example Determine the elements of [A] for a symmetric laminate of 6 layers: [0/45/90] s. The material of each lamina is Gr/Ep T 300/5208 and t=0. 005” = 0. 000125 m 0° Lamina 90° Lamina Q 11 = Qxx = 181. 8 Q 11 = Qyy = 10. 34 Q 22 = Qxx = 181. 8 Q 12 = Qxy = 2. 897 Q 66 = Qss = 7. 17 Q 16 = 0 Q 26 = 0 Q 11 = Qxx cos 4θ + 2 (Qxy + 2 Qss) sin 2θ cos 2θ + Qyy sin 4θ Q 22 = Qxx sin 4θ + 2 (Qxy + 2 Qss) sin 2θ cos 2θ + Qyy cos 4θ Q 12 = Q 21 = (Qxx + Qyy – 4 Qss) sin 2θ cos 2θ + Qxy (sin 4θ + cos 4θ) Q 66 = (Qxx + Qyy – 2 Qxy – 2 Qss) sin 2θ cos 2θ + Qss (sin 4θ + cos 4θ) Q 16 = Q 61 = (Qxx – Qxy – 2 Qss) sinθ cos 3θ + (Qxy – Qyy + 2 Qss) sin 3θ cosθ Q 26 = Q 62 = (Qxx – Qxy – 2 Qss) sin 3θ cosθ + (Qxy – Qyy + 2 Qss) sinθ cos 3θ Q 11 = 0. 25 Qxx + 2 (Qxy + 2 Qss) (0. 25) + 0. 25 Qyy = 56. 65

Q 22 = 0. 25 Qxx + 2 (Qxy + 2 Qss) (0. 25) + 0. 25 Qyy = 56. 65 Q 12 = (Qxx + Qyy – 4 Qss) (0. 25) + Qxy (0. 5) = 42. 31 Q 66 = (Qxx + Qyy – 2 Qxy – 2 Qss) (0. 25) + Qss (0. 25) = 46. 59 Q 16 = (Qxx – Qxy – 2 Qss) (0. 25) + (Qxy – Qyy +2 Qss) (0. 25) = 42. 87 Q 26 = (Qxx – Qxy – 2 Qss) (0. 25) + (Qxy – Qyy +2 Qss) (0. 25) = 42. 87 The Laminate A 11 = 0. 000125 (181. 8 + 10. 34 + 56. 25) 2 = 0. 0622 A 22 = 0. 000125 (10. 34 + 181. 8 + 56. 65) 2 = 0. 0622 A 12 = 0. 000125 (2. 897 + 42. 31) 2 = 0. 0120 A 66 = 0. 000125 (7. 17 + 46. 59) 2 = 0. 0152 A 16 = 0. 000125 (0 + 42. 87) 2 = 0. 0107 A 26 = 0. 000125 (0 + 42. 87) 2 = 0. 0107 GPa-m

Equivalent Engineering Constants for the Laminate Equation for the composite laminate is Or [N] = [A] [ε] Matrix equation for a single orthotropic lamina or layer is Or [σ] = [M] [ε]

The properties of the single “equivalent” orthotropic layer can be determined from the following equation: or [A] = [M] A 11 = where h = laminate thickness A 12 = A 66 = E 6 A 22 = A 21 = Solving last equation, we have the following elastic constants for the single “equivalent” orthotropic layer: E 1 = (1 – ) E 2 = (1 – ) E 6 = A 66 ν 1 = ν 2 =

The equation for the composite laminate is or where [ε] = [a] [N] [a] = [A] -1 The equation for a single orthotropic lamina is or [ε] = [C] [σ]

The properties of the single “equivalent” orthotropic layer is determined by [a] h = [C] or a 11 h = a 12 h = a 21 h = a 22 h = a 66 h = elastic constants for the single “equivalent” orthotropic layer: E 1 = E 2 = ν 1 = – ν 2 = – E 66 =

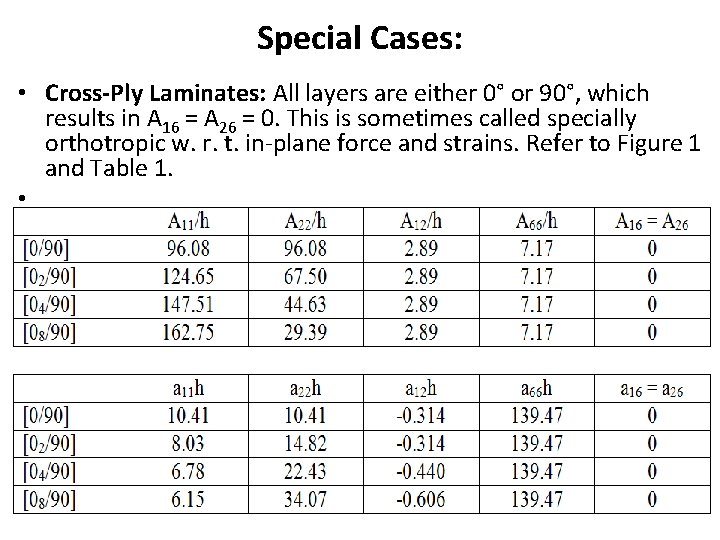
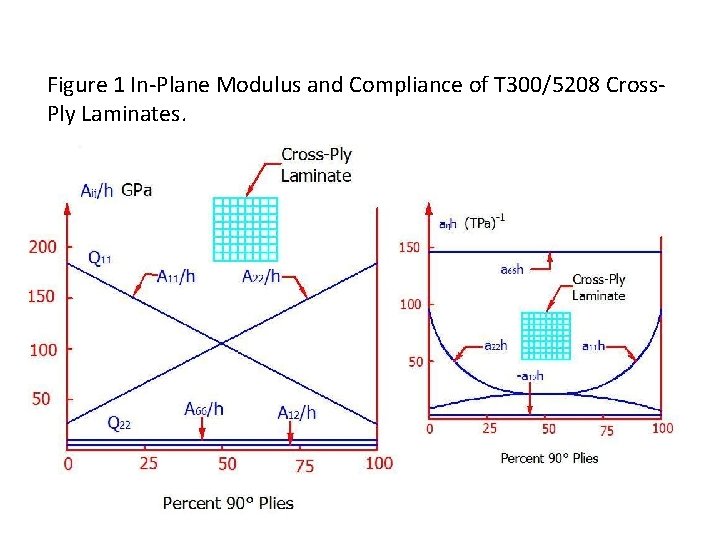
Special Cases: • Cross-Ply Laminates: All layers are either 0° or 90°, which results in A 16 = A 26 = 0. This is sometimes called specially orthotropic w. r. t. in-plane force and strains. Refer to Figure 1 and Table 1. • • h = total laminate thickness

Figure 1 In-Plane Modulus and Compliance of T 300/5208 Cross. Ply Laminates.

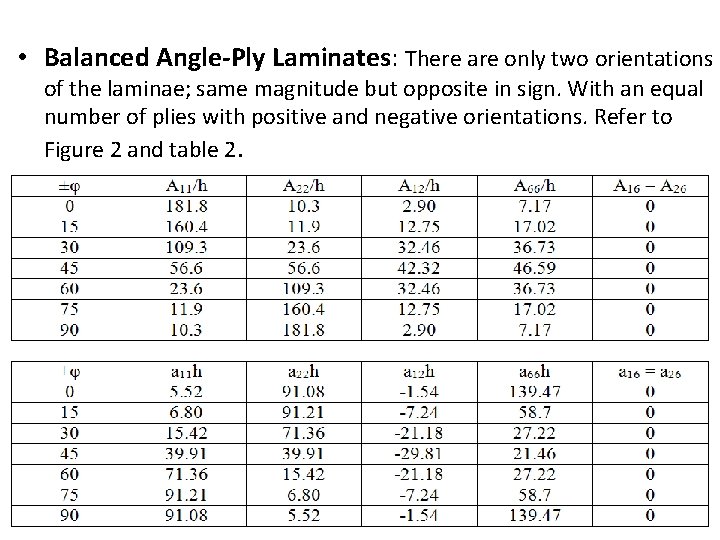
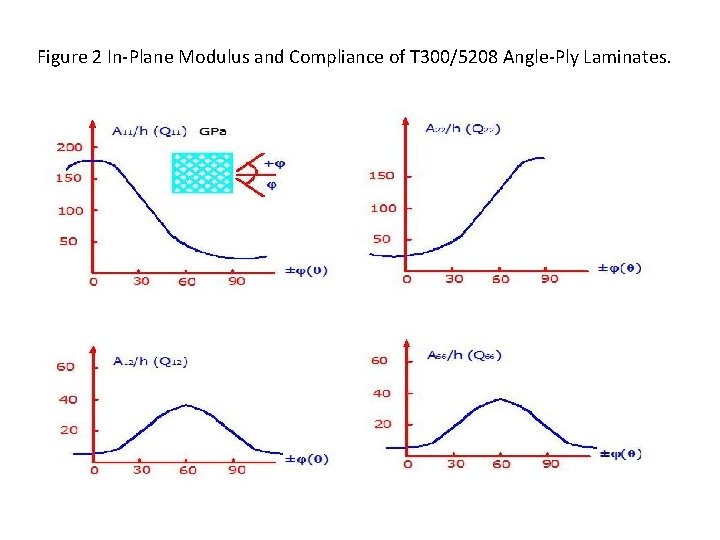
• Balanced Angle-Ply Laminates: There are only two orientations of the laminae; same magnitude but opposite in sign. With an equal number of plies with positive and negative orientations. Refer to Figure 2 and table 2. • h = total laminate thickness.

Figure 2 In-Plane Modulus and Compliance of T 300/5208 Angle-Ply Laminates.

The balanced angle-ply laminate is another case of “special orthotropy” w. r. t. inplane force and strains; that is A 16 = A 26 = 0. The values of Table 2 apply for un-symmetric laminate as well as symmetric laminates. For example, the values for [+30, − 30, +30, − 30] or [+30, − 30] are the same as those for [+30, -30, +30]. If the laminate is not balanced, such as [+30, − 30, +30], then the terms A 16 and A 26 are not zero. Also remember that A 16 = A 26 for all cross-plies, whether they are symmetric or unsymmetric. Example: [0, 90] [0, 90, 0] [+30, − 30, +30] [+30, − 30, +30, − 30] [+30, − 30, +30] un-symmetric cross-ply, A 16 = A 26 = 0 symmetric balanced angle-ply, A 16 = A 26 = 0 un-symmetric balanced angle-ply, A 16 = A 26 = 0 symmetric un-balanced angle-ply, A 16, A 26 ≠ 0

3) Quasi-Isotropic Laminates: Has ‘m’ ply groups spaced at ply orientations of 180/m degrees. Note: This does not apply for m = 1 and m = 2. The laminate need not be symmetric to be quasi-isotropic. For example, the laminate [0, 45, − 45, 90] is quasi-isotropic. Examples: [0/60/− 60]s [0/90/45/− 45]s [0/60/− 60/60/0/− 60]s m = 3 m = 4 m=3 180/m = 60° 180/m = 45° 180/m = 60° The modulus of the quasi-isotropic laminate has the following properties: A 11 = A 22 A 16 = A 26 = 0 A 66 = (A 11 – A 22) which is equivalent to G = for an isotropic material.

Summary: Laminate Analysis