Compiler Construction Sohail Aslam Lecture 25 Sets of

Compiler Construction Sohail Aslam Lecture 25

Sets of LR(1) Items I 0 ={ [S → E, $], [E → E+(E), $/+], [E → int, $/+] } 2

The Closure Procedure Rationale: § if [A → b Cd, a] s, then one potential completion for the left context is to find a string that reduces to C, followed by da 3

The Closure Procedure § This completion should cause a reduction to A, since it fills out the production’s righthand side (Cd), and follows it with a valid lookahead symbol 4

The Closure Procedure § For a production C → g, closure must insert ' ' before g and add appropriate lookahead symbols – all terminals that can appear as the initial symbol in da 5

The Closure Procedure § This includes every terminal in FIRST(d). If e FIRST(d), it also includes a, thus FIRST(da) in the algorithm 6

The goto Procedure § The second critical step in the construction is to derive other parser states from I 0 7

The goto Procedure § To accomplish this, we compute, for each state Ii and each grammar symbol y, the state that would arise if the parser recognized an y while in state Ii 8

The goto Procedure § A state s that contains [X → a yb, b] has a transition (goto) labeled y to the state that contains the items goto(s, y) • y can be terminal or a nonterminal 9

goto(s, y) m {} for each item [X → a yb, b] s m ← m {[X → ay b, b]} return closure(m) 10

Finite Automaton of Items § The LR(1) items are used as the states of a finite automaton that maintains information about the parsing stack and progress of a shiftreduce parser 11

Finite Automaton of Items § This will start out as a nondeterministic finite automaton (NFA) § The DFA can be constructed from this NFA using the subset construction, similar to one we used for lexical analysis 12

Finite Automaton of Items § This will start out as a nondeterministic finite automaton (NFA) § The DFA can be constructed from this NFA using the subset construction, similar to one we used for lexical analysis 13

Finite Automaton of Items § What are the transitions of the NFA of LR(0) items? § Consider the item A→ a g § Suppose g begins with symbol X which may be a terminal (token) or non-terminal 14

Finite Automaton of Items § What are the transitions of the NFA of LR(0) items? § Consider the item A→ a g § Suppose g begins with symbol X which may be a terminal (token) or non-terminal 15

Finite Automaton of Items § What are the transitions of the NFA of LR(0) items? § Consider the item A→ a g § Suppose g begins with symbol X which may be a terminal (token) or non-terminal 16

Finite Automaton of Items § The item can be written as A→ a Xh § Then there is a transition on symbol X for state represented by item A→ a Xh to state represented by item A→ a. X h 17

Finite Automaton of Items § The item can be written as A→ a Xh § Then there is a transition on symbol X for state represented by item A→ a Xh to state represented by item A→ a. X h 18

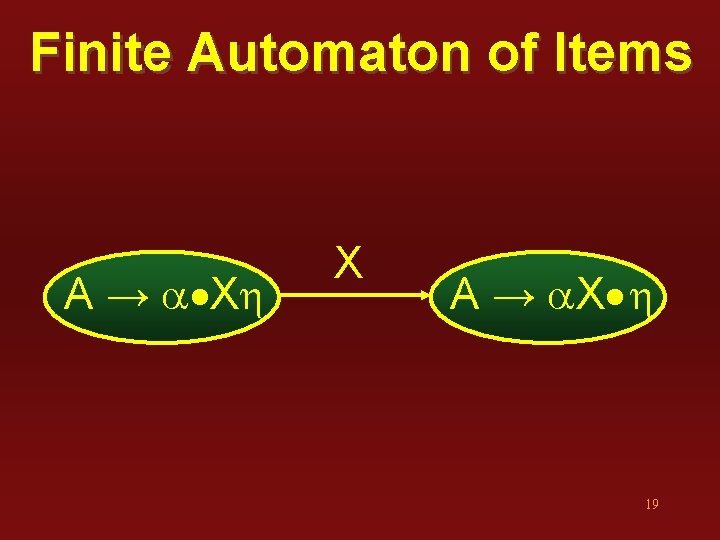
Finite Automaton of Items A → a Xh X A → a. X h 19

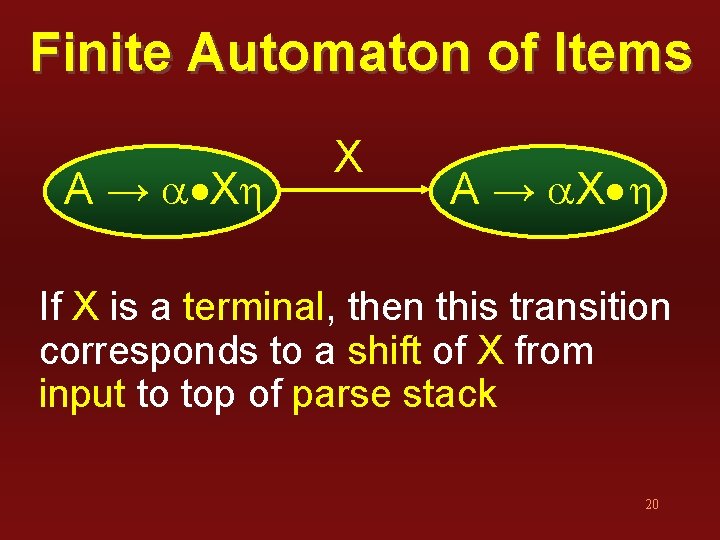
Finite Automaton of Items A → a Xh X A → a. X h If X is a terminal, then this transition corresponds to a shift of X from input to top of parse stack 20

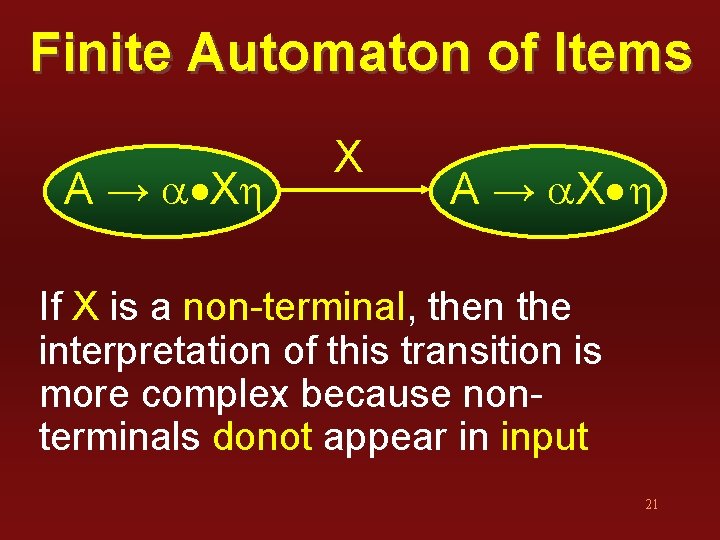
Finite Automaton of Items A → a Xh X A → a. X h If X is a non-terminal, then the interpretation of this transition is more complex because nonterminals donot appear in input 21

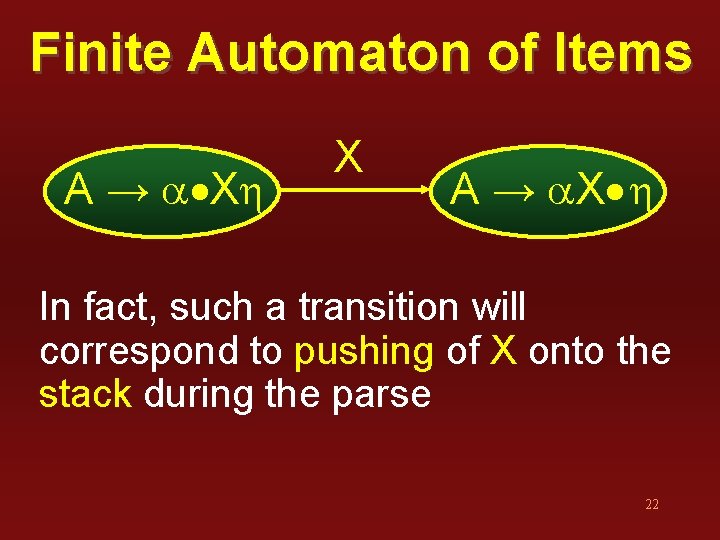
Finite Automaton of Items A → a Xh X A → a. X h In fact, such a transition will correspond to pushing of X onto the stack during the parse 22

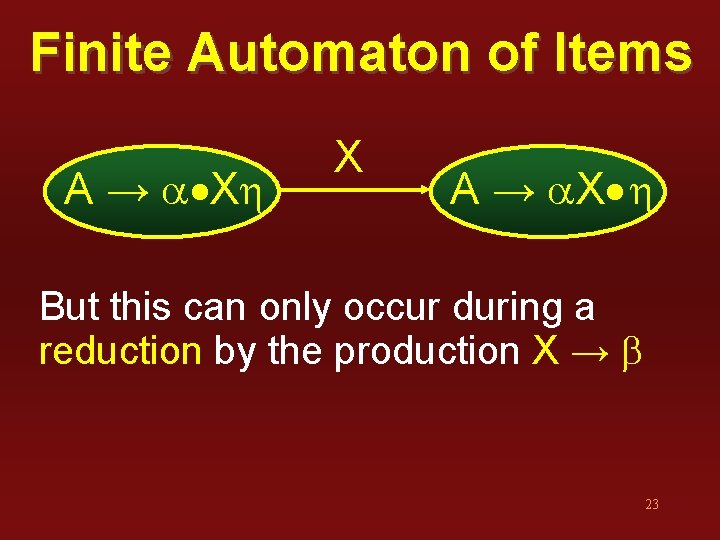
Finite Automaton of Items A → a Xh X A → a. X h But this can only occur during a reduction by the production X → b 23

Finite Automaton of Items A → a Xh X A → a. X h Such a reduction must be preceded by recognition of a b 24

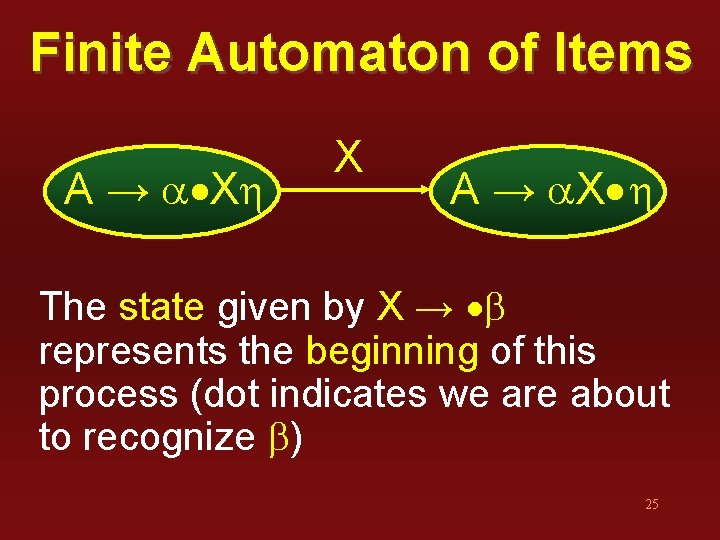
Finite Automaton of Items A → a Xh X A → a. X h The state given by X → b represents the beginning of this process (dot indicates we are about to recognize b) 25