Compiler Construction Sohail Aslam Lecture 6 How to

Compiler Construction Sohail Aslam Lecture 6

How to Describe Tokens? § Regular Languages are the most popular for specifying tokens • Simple and useful theory • Easy to understand • Efficient implementations 2

Languages § Let S be a set of characters. S is called the alphabet. § A language over S is set of strings of characters drawn from S. 3

Example of Languages Alphabet = English characters Language = English sentences Alphabet = ASCII Language = C++ programs, Java, C# 4

Notation § Languages are sets of strings (finite sequence of characters) § Need some notation for specifying which sets we want 5

Notation § For lexical analysis we care about regular languages. § Regular languages can be described using regular expressions. 6

Regular Languages § Each regular expression is a notation for a regular language (a set of words). § If A is a regular expression, we write L(A) to refer to language denoted by A. 7

Regular Expression § A regular expression (RE) is defined inductively a ordinary character from S e the empty string 8

Regular Expression R|S RS R* = either R or S = R followed by S (concatenation) = concatenation of R zero or more times (R*= e |R|RR|RRR. . . ) 9

RE Extentions R? R+ (R) = e | R (zero or one R) = RR* (one or more R) = R (grouping) 10

RE Extentions [abc] = a|b|c (any of listed) [a-z] = a|b|. . |z (range) [^ab] = c|d|. . . (anything but ‘a’‘b’) 11

Regular Expression RE Strings in L(R) a “a” ab “ab” a|b “a” “b” (ab)* “” “abab”. . . (a|e)b “ab” “b” 12

Example: integers § integer: a non-empty string of digits § digit = ‘ 0’|’ 1’|’ 2’|’ 3’|’ 4’| ’ 5’|’ 6’|’ 7’|’ 8’|’ 9’ § integer = digit* 13

Example: identifiers § identifier: string or letters or digits starting with a letter § C identifier: [a-z. A-Z_][a-z. A-Z 0 -9_]* 14

Recap Tokens: strings of characters representing lexical units of programs such as identifiers, numbers, operators. 15

Recap Regular Expressions: concise description of tokens. A regular expression describes a set of strings. 16

Recap Language L(R): set of strings represented by a regular expression R. L(R) is the language denoted by regular expression R. 17

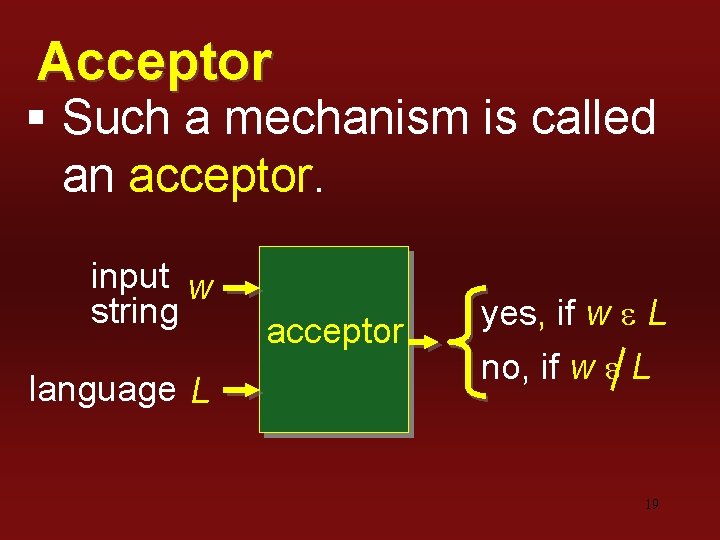
How to Use REs § We need mechanism to determine if an input string w belongs to L(R), the language denoted by regular expression R. 18

Acceptor § Such a mechanism is called an acceptor. input w string language L acceptor yes, if w e L no, if w e L 19

Finite Automata (FA) § Specification: Regular Expressions § Implementation: Finite Automata 20

Finite Automata Finite Automaton consists of § An input alphabet (S) § A set of states § A start (initial) state § A set of transitions § A set of accepting (final) states 21

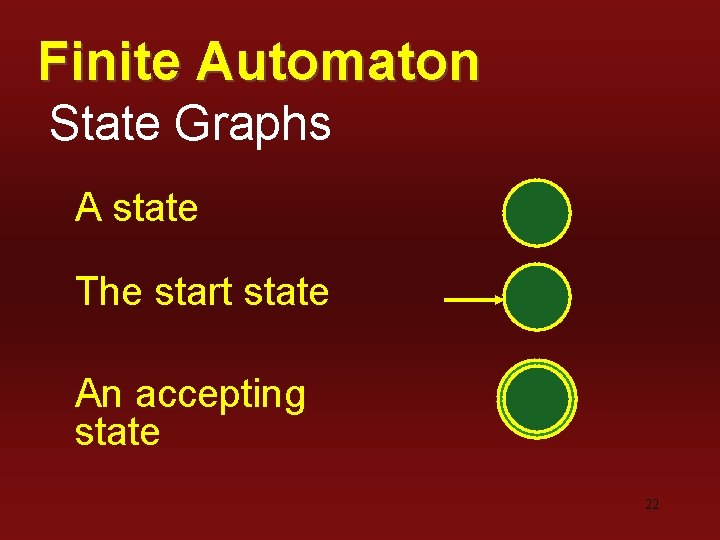
Finite Automaton State Graphs A state The start state An accepting state 22

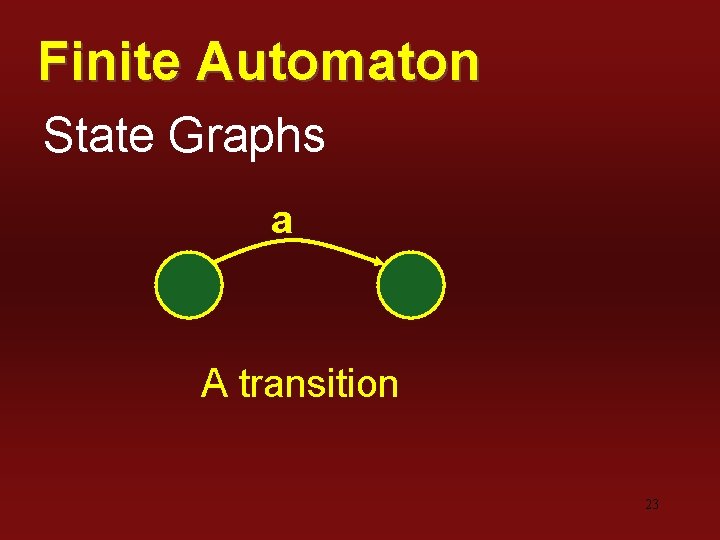
Finite Automaton State Graphs a A transition 23

Finite Automata § A finite automaton accepts a string if we can follow transitions labelled with characters in the string from start state to some accepting state. 24

FA Example A FA that accepts only “ 1” 1 25

FA Example § A FA that accepts any number of 1’s followed by a single 0 1 0 26

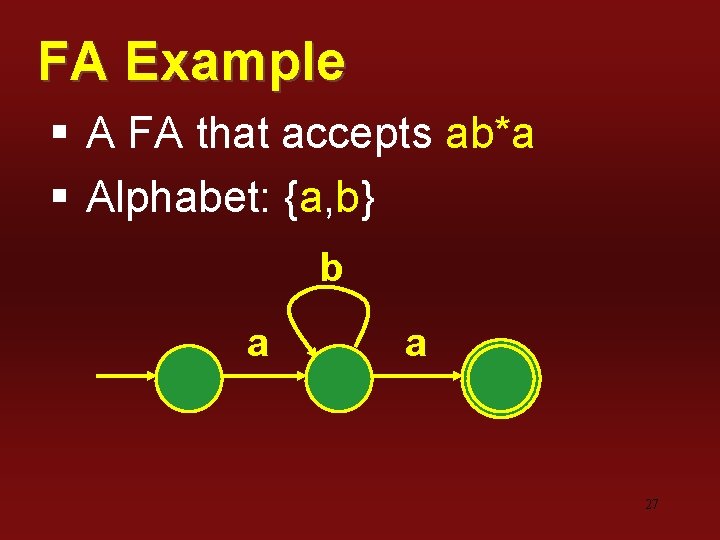
FA Example § A FA that accepts ab*a § Alphabet: {a, b} b a a 27