CMSC 202 Trees Tree Definitions 1 A tree

CMSC 202 Trees

Tree Definitions 1. A tree is a set of nodes 2. The set of nodes may be empty 3. If not empty, there is a distinguished node, r, called the root and zero or more nonempty subtrees T 1, T 2, T 3, …. Tk, each of whose roots is connected by a directed edge from r. 4. As item #3 indicates, trees are recursive in their definition and therefore in their implementation. 2

Basic Tree Terminology • Tree terminology takes its terms from both nature and genealogy. • The root of each subtree is a child of r, and r is called its parent. • A node with one or more children is called an internal node. • All children of the same internal node are called siblings. • A node with no children is called a leaf or external node. 3

Path in a Tree • A path in a tree is a sequence of nodes, (N 1, N 2, … Nk) such that Ni is the parent of Ni+1 for 1 <= i <= k. • The length of this path is the number of edges encountered (k – 1) • If there is a path from node N 1 to N 2, then N 1 is an ancestor of N 2 and N 2 is a descendant of N 1. 4

Height/Depth of a Node • The depth of a node is the length of the path from the root to the node • The height of a node is the length of the longest path from the node to a leaf 5

Height/Depth of a Tree • The depth of a tree is the depth of its deepest leaf. • The height of a tree is the height of the root. • True or False – the height of a tree and the depth of a tree always have the same value 6

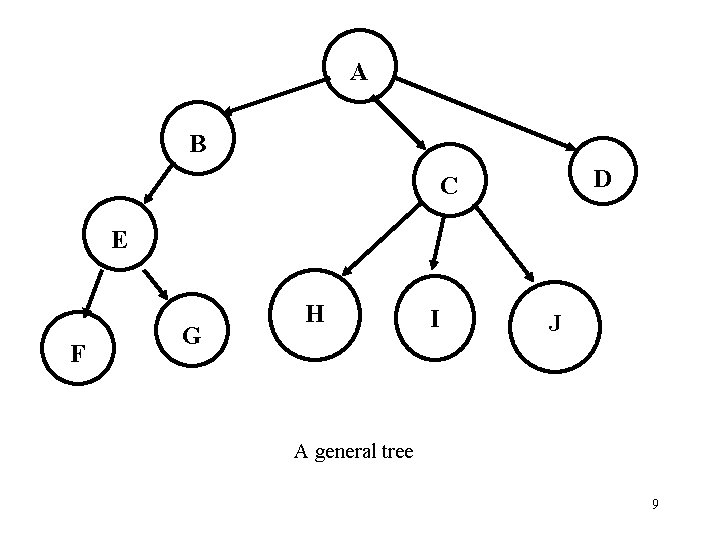
Tree Storage • First attempt - each tree node contains – The data element being stored • We assume that the objects contained in the nodes support all necessary operations required by the tree – Links to all of its children • Problem: A tree node can have an indeterminate number of children. So how many links do we define in the node? 7

First Child, Next Sibling • Since we can’t know how many children a node can have, we can’t create a static data structure… we need a dynamic one. • Each node will contain – The data object which supports all necessary operations – A link to its first child – A link to a sibling 8

A B D C E F G H I J A general tree 9

First Child, Next Sibling Representation • To be supplied in class 10

Breadth-First Tree Traversals • • Start at the root “Visit” all the root’s children Then “visit” all the root’s grand-children Then “visit” all the roots great-grandchildren • And so on, and so on • This traversal goes down by levels • A queue application 11

BF Traversal pseudo-code Create a queue, Q, to hold tree nodes Q. enqueue (the root) while (the queue is not empty) Node N = Q. dequeue( ) for each child, X, of N Q. enqueue (X) • The order in which the nodes are dequeued is the BF traversal order 12

Depth-First Traversal • • • Start at the root Choose a child to “visit” “Visit” all of that child’s children’s children Etc. , etc. • This traversal goes down a path until the end, then comes back and does the next path • A stack application 13

DF Traversal Pseudo-Code Create a Stack, S, to hold tree nodes S. push (the root) While (the stack is not empty) Node N = S. pop ( ) for each child, X, of N S. push (X) The order in which the nodes are popped is the DF traversal order 14

Performance of BF and DF traversals • What is the asymptotic performance of Breadth-first and Depth-first traversals on a general tree? • Since the traversals “visit” every node in the tree, their performance is O(n), in all cases, where n is the number of nodes in the tree 15

Other functions • These fundamental functions could be written recursively with few lines of code – Count. Nodes – given a pointer to the root of a tree, count the number of nodes in the tree – Depth – given a pointer to the root of a tree, determine the tree’s depth 16

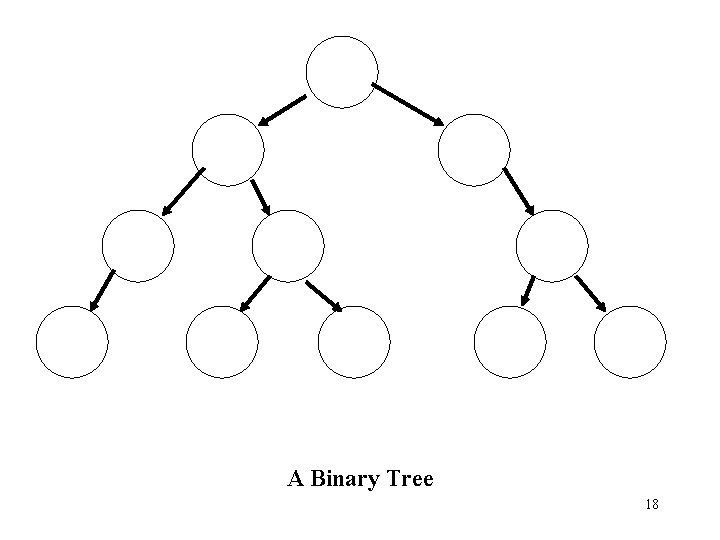
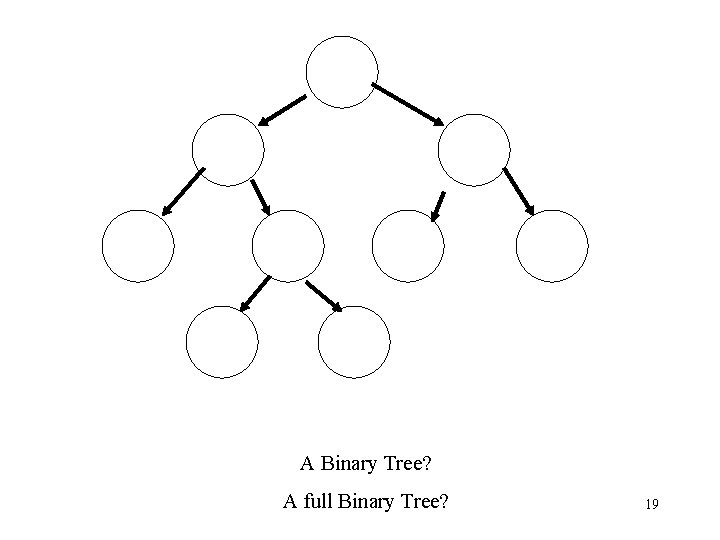
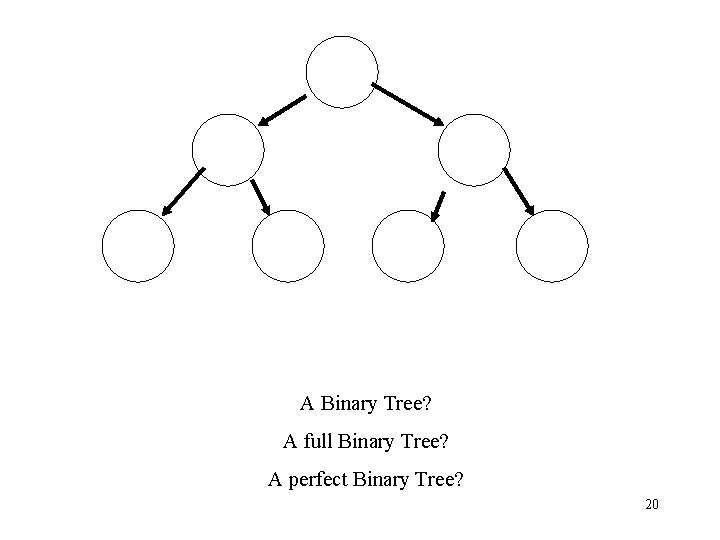
Binary Tree Definitions • A binary tree is a rooted tree in which each node has just two children AND the children are designated as left and right. • A full binary tree is one in which each node has either two children or is a leaf • A perfect binary tree is a full binary tree in which all leaves are at the same level 17

A Binary Tree 18

A Binary Tree? A full Binary Tree? 19

A Binary Tree? A full Binary Tree? A perfect Binary Tree? 20

Binary Tree Traversals • Because nodes in binary trees have just two children (left and right), we can write specialized versions of BF and DF traversals. These are called – In-order traversal – Pre-order traversal – Post-order traversal – Level-order traversal 21

In-Order traversal • At each node – “visit” my left child first – “visit” me – “visit” my right child last • A recursive function should you be able to write 22

Post-Order traversal • At each node – “visit” my left child first – “visit” my right child next – “visit” me last • A recursive routine you should be able to write 23

Pre-Order Traversal • At each node – “visit” me last first – “visit” my left child next – “visit” my right child last • A recursive routine you should be able to write 24

Binary Tree Operations • Recall that the object stored in the nodes support all necessary operators. We’ll refer to it as a “value” and use integers for our examples • • • Create an empty tree Insert a new value Search (find) a value Remove a value Destroy the tree 25

Creating an Empty Tree • Set the pointer to the root equal to NULL 26

Inserting into a Binary Tree • The first value goes in the root node • What about the second value? • What about subsequent values? • Since the tree has no properties which dictate where the values should be stored, we are at liberty to choose our own algorithm for storing the data 27

Searching in a Binary Tree • How do we find a value in a binary tree? • Since there is no rhyme or reason to where the values are stored, we must search the entire tree using a BF or DF traversal 28

Removing a value from the tree • Once again, since the values are not stored in any special way, we have lots of choices • First, find the value via BF or DF traversal • Second, replace it with one of its children (if there any). 29

Destroying a Tree • We have to be careful of the order in which nodes are destroyed • We have to destroy the children first, and the parent last (because the parent points to the children) 30

Giving Order to a Binary Tree • Binary trees can be made more useful if we dictate the manner in which values are stored • When selecting where to insert new values, follow this rule: – “left is less” – “right is more” 31

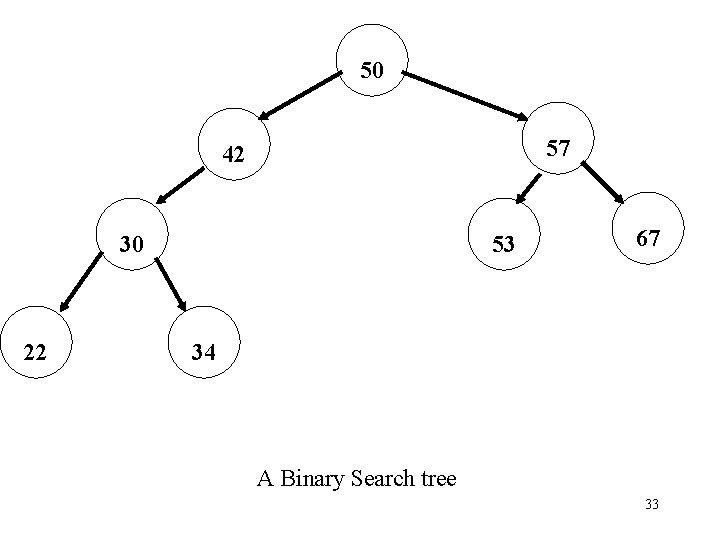
The Binary Search Tree Definition – A Binary Search tree is a binary tree with the additional property that at each node, the value in the node’s left child is smaller than the value in the node itself, and the value in the node’s right child is larger than the value in the node itself 32

50 57 42 30 22 53 67 34 A Binary Search tree 33

Searching a BST • Searching for the value X, given a pointer to the root 1. If the value in the root matches, we’re done 2. If X is smaller than the value in the root, look in the root’s left subtree 3. If X is larger than the value in the root, look in the root’s right subtree • A recursive routine – what’s the base case? 34

Inserting a new value in a BST • To insert value X in a BST 1. Proceed as if searching for X 2. When the search fails, create a new node to contain X and attach it to the tree at that node 35

Removing a value from a BST • Non-trivial • We just can’t replace the node containing X with one of it’s children. • Why not? • What do we do instead? – There are three cases to examine 36

Destroying a BST • The fact that the values in the nodes are in a special order doesn’t help • We still have to destroy each child before destroying the parent • Which traversal can we use? 37

Performance in a BST • Is the performance of insert, search and remove improved? • If so, why? • If not, why not? 38