CHAPTER 7 MAGNETOSTATIC FIELD STEADY MAGNETIC 7 1

CHAPTER 7 MAGNETOSTATIC FIELD (STEADY MAGNETIC) 7. 1 INTRODUCTION - SOURCE OF MAGNETOSTATIC FIELD 7. 2 ELECTRIC CURRENT CONFIGURATIONS 7. 3 BIOT SAVART LAW 7. 4 AMPERE’S CIRCUITAL LAW 7. 5 CURL (IKAL) 7. 6 STOKE’S THEOREM 7. 7 MAGNETIC FLUX DENSITY 7. 8 MAXWELL’S EQUATIONS 7. 9 VECTOR MAGNETIC POTENTIAL 1

7. 1 INTRODUCTION - SOURCE OF MAGNETOSTATIC FIELD Originate from: • constant current • permanent magnet • electric field changing linearly with time

Analogous between electrostatic and magnetostatic fields Attribute Electrostatic Magnetostatic Source Static charge Steady current Field Factor Related Maxwell equations Potential Energy density Scalar V with

Two important laws – for solving magnetostatic field • Biot Savart Law – general case • Ampere’s Circuital Law – cases of symmetrical current distributions

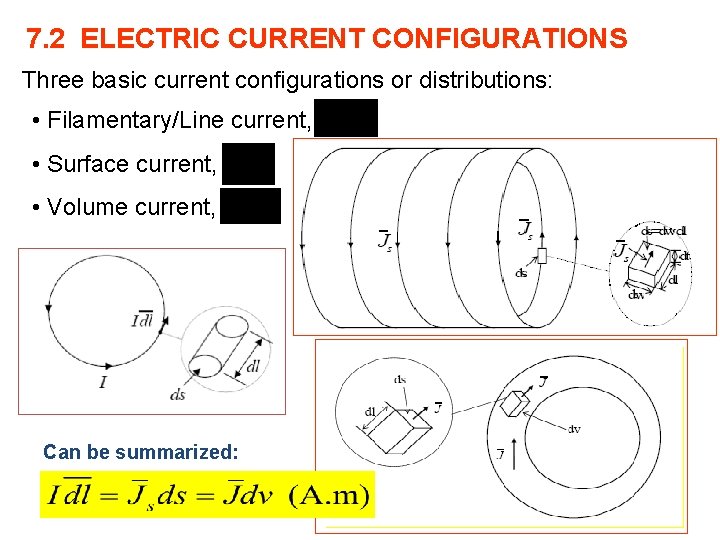
7. 2 ELECTRIC CURRENT CONFIGURATIONS Three basic current configurations or distributions: • Filamentary/Line current, • Surface current, • Volume current, Can be summarized:

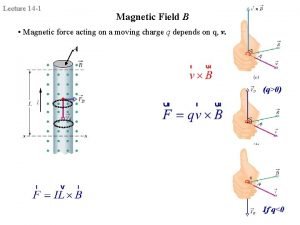
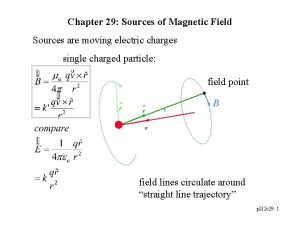
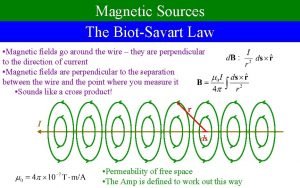
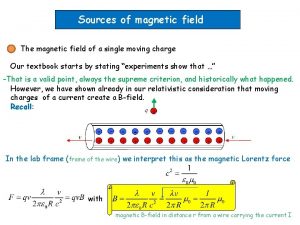
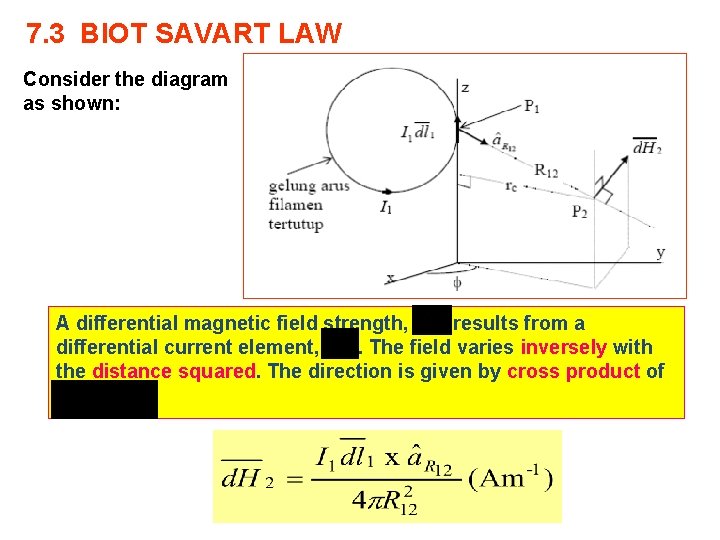
7. 3 BIOT SAVART LAW Consider the diagram as shown: A differential magnetic field strength, results from a differential current element, . The field varies inversely with the distance squared. The direction is given by cross product of

Total magnetic field can be obtained by integrating: Similarly for surface current and volume current elements the magnetic field intensities can be written as:

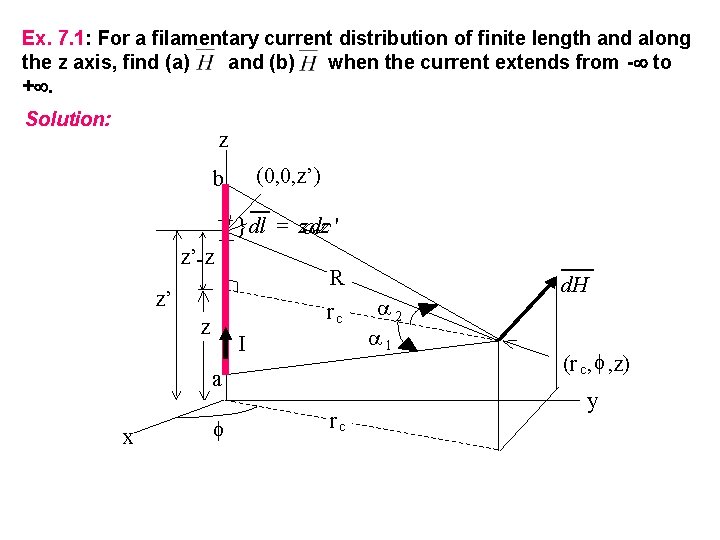
Ex. 7. 1: For a filamentary current distribution of finite length and along the z axis, find (a) and (b) when the current extends from - to +. Solution: z (0, 0, z’) b } dl = z$ dz ' z’- z R z’ rc z I a x f rc 2 1 d. H (r c , f , z) y

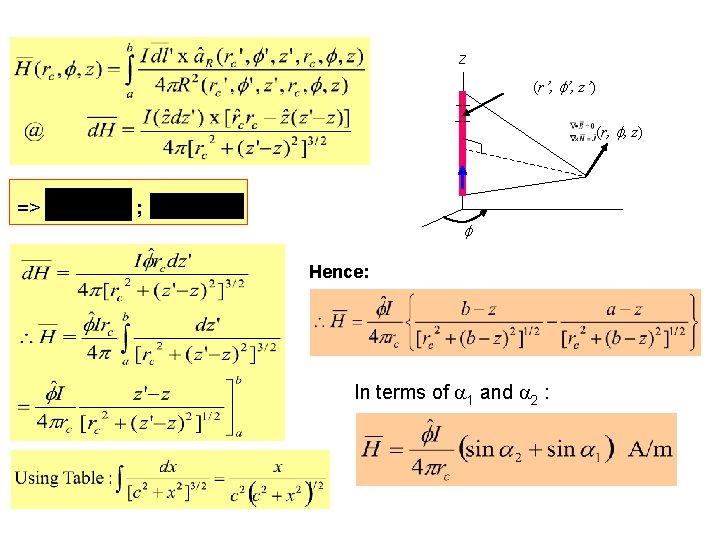
z (r’, ’, z’) (r, , z) => ; Hence: In terms of 1 and 2 :

(b) When a = - and b = + , we see that 1 = /2, and 2 = /2 The flux of in the direction and its density decrease with rc as shown in the diagram.

Ex. 7. 2: Find the expression for the field along the axis of the circular current loop carrying a current I. Solution: Using Biot Savart Law and where the component was omitted due to symmetry

Hence:

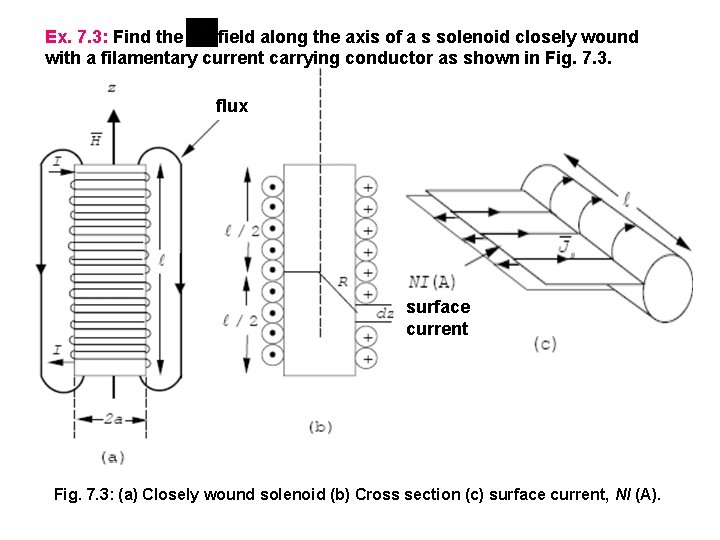
Ex. 7. 3: Find the field along the axis of a s solenoid closely wound with a filamentary current carrying conductor as shown in Fig. 7. 3. flux surface current Fig. 7. 3: (a) Closely wound solenoid (b) Cross section (c) surface current, NI (A).

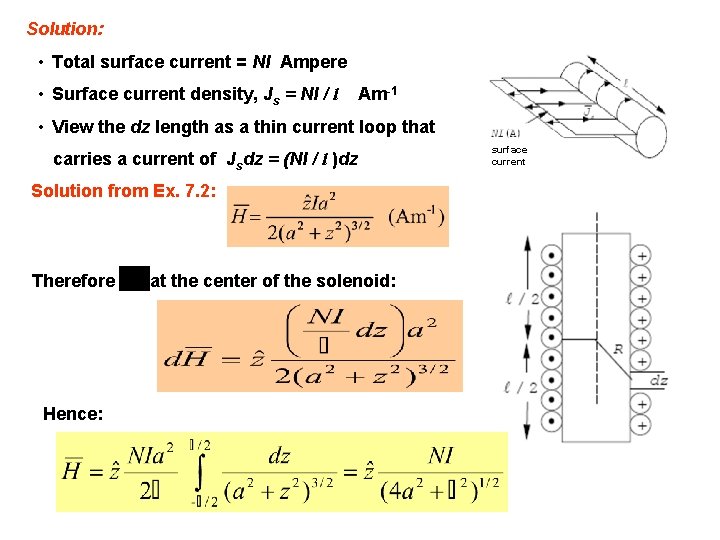
Solution: • Total surface current = NI Ampere • Surface current density, Js = NI / l Am-1 • View the dz length as a thin current loop that carries a current of Jsdz = (NI / l )dz Solution from Ex. 7. 2: Therefore Hence: at the center of the solenoid: surface current

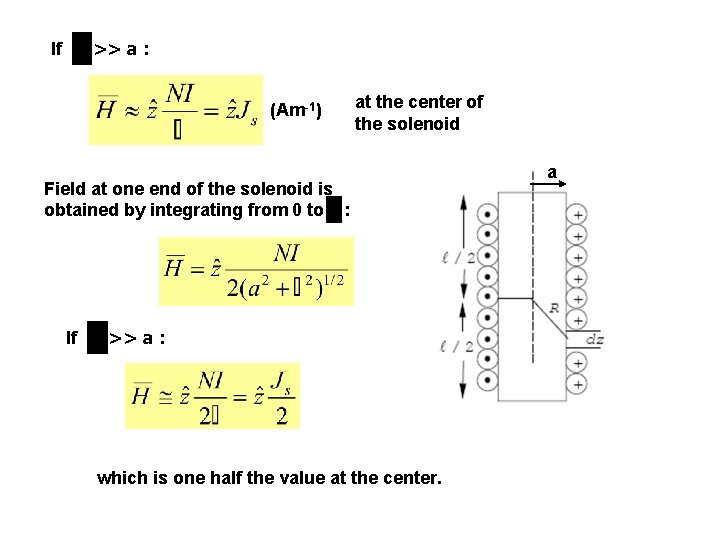
>> a : If (Am-1) at the center of the solenoid Field at one end of the solenoid is obtained by integrating from 0 to : If >> a : which is one half the value at the center. a

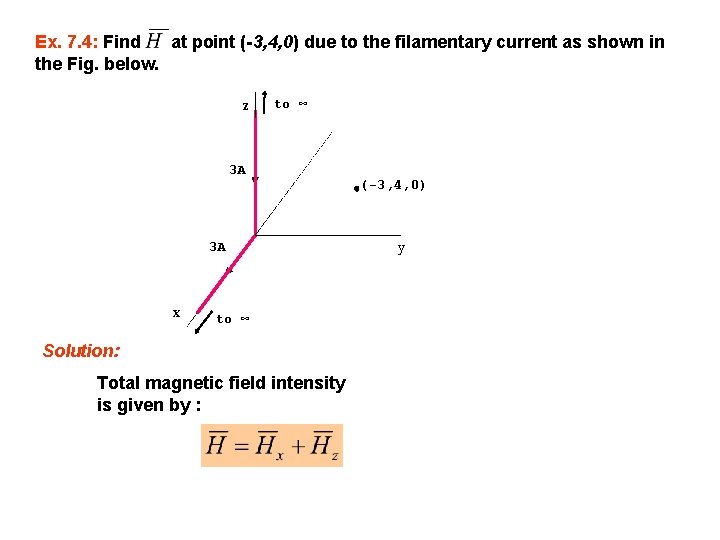
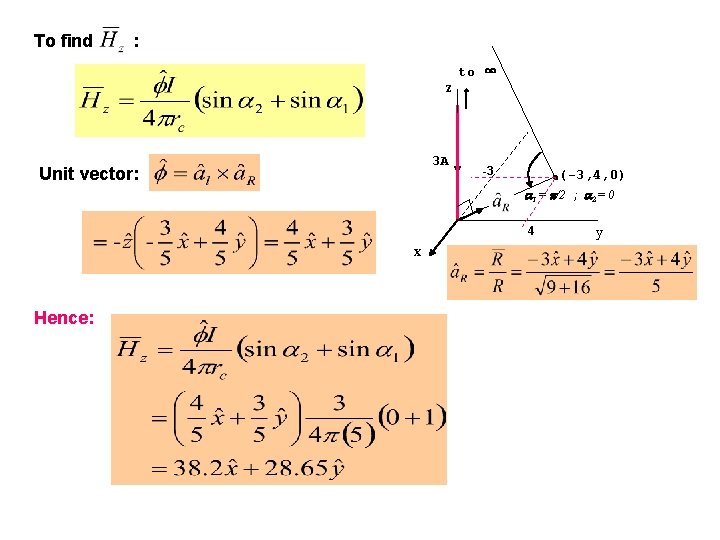
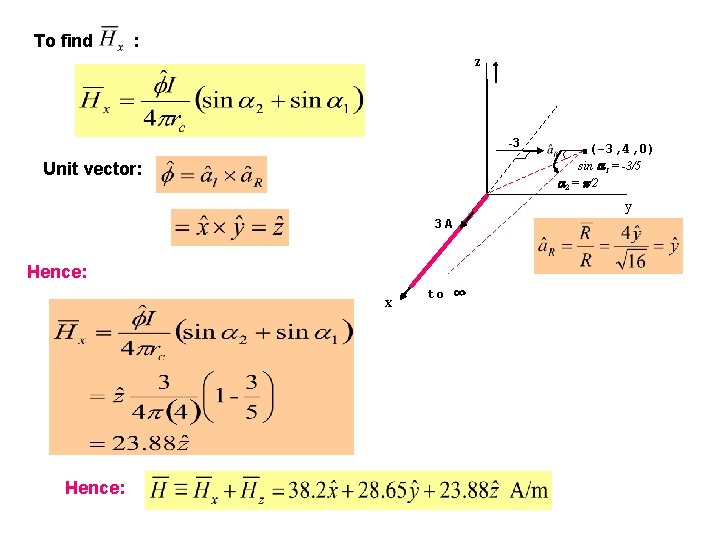
Ex. 7. 4: Find at point (-3, 4, 0) due to the filamentary current as shown in the Fig. below. z to ∞ 3 A 3 A x to ∞ Solution: Total magnetic field intensity is given by : (-3, 4, 0) y

To find : z 3 A Unit vector: to ∞ -3 (-3, 4, 0) 1 = /2 ; 2 = 0 4 x Hence: y

To find : z -3 (-3, 4, 0) sin 1 = -3/5 2 = /2 Unit vector: y 3 A Hence: x Hence: to ∞

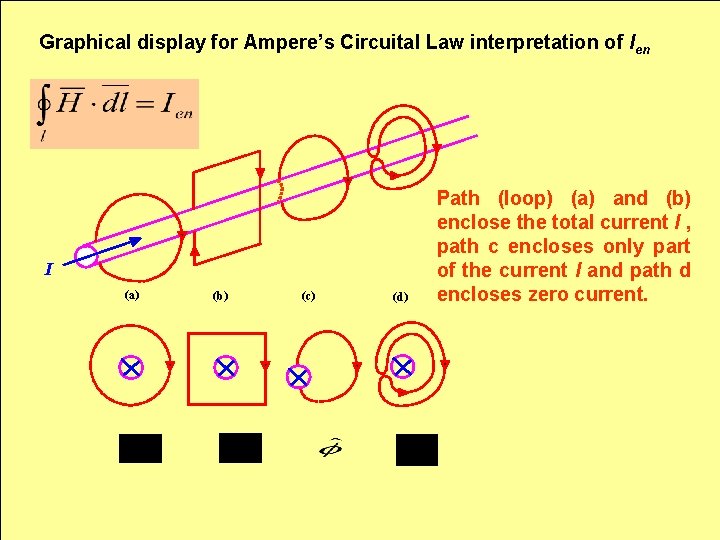
7. 4 AMPERE’S CIRCUITAL LAW • Solving magnetostaic problems for cases of symmetrical current distributions. Definition: The line integral of the tangential component of the magnetic field strength around a closed path is equal to the current enclosed by the path :

Graphical display for Ampere’s Circuital Law interpretation of Ien I (a) (b) (c) (d) Path (loop) (a) and (b) enclose the total current I , path c encloses only part of the current I and path d encloses zero current.

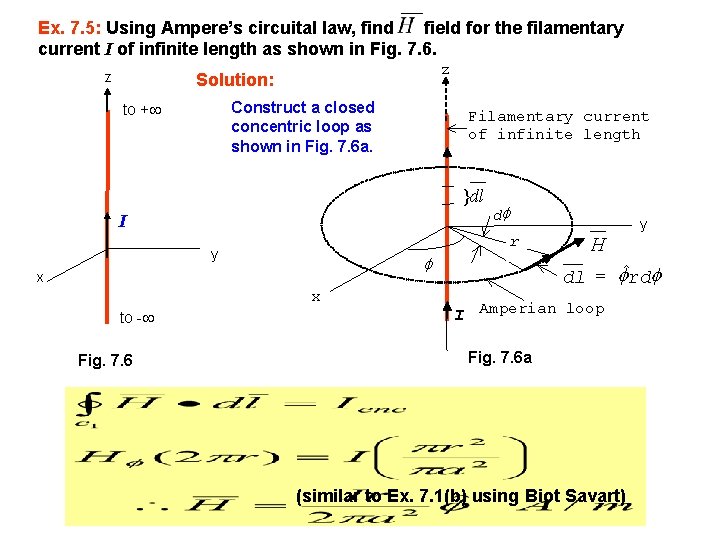
Ex. 7. 5: Using Ampere’s circuital law, find field for the filamentary current I of infinite length as shown in Fig. 7. 6. z z Solution: Construct a closed concentric loop as shown in Fig. 7. 6 a. to + Filamentary current of infinite length }dl I r y x x to - Fig. 7. 6 d y H dl = ˆrd I Amperian loop Fig. 7. 6 a (similar to Ex. 7. 1(b) using Biot Savart)

Ex. 7. 5: Find inside and outside an infinite length conductor of infinite cross section that carries a current I A uniformly distributed over its cross section and then plot its magnitude. y Solution: For r a (C 2) : conductor C 2 C 1 x I a Amperian path r H(r) For r ≤ a (C 1) : H(a) = I/2πa H 1 H 2 a r

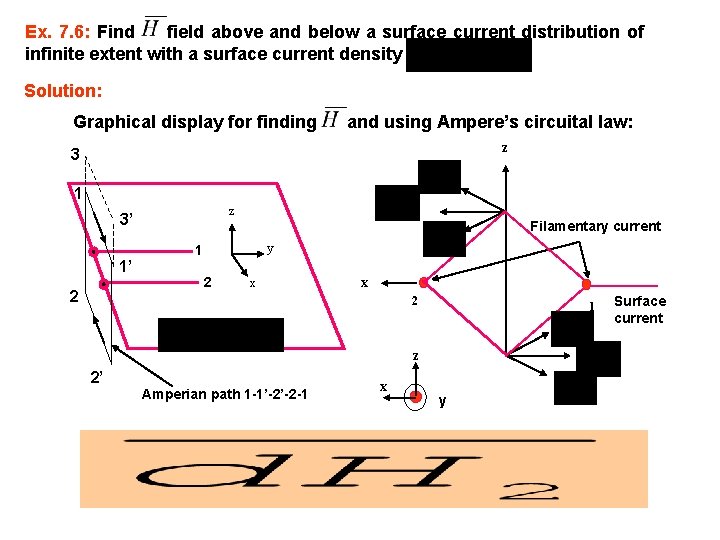
Ex. 7. 6: Find field above and below a surface current distribution of infinite extent with a surface current density Solution: Graphical display for finding and using Ampere’s circuital law: z 3 1 z 3’ 1’ 2 Filamentary current y 1 2 x x 2 1 z 2’ Amperian path 1 -1’-2’-2 -1 x y Surface current

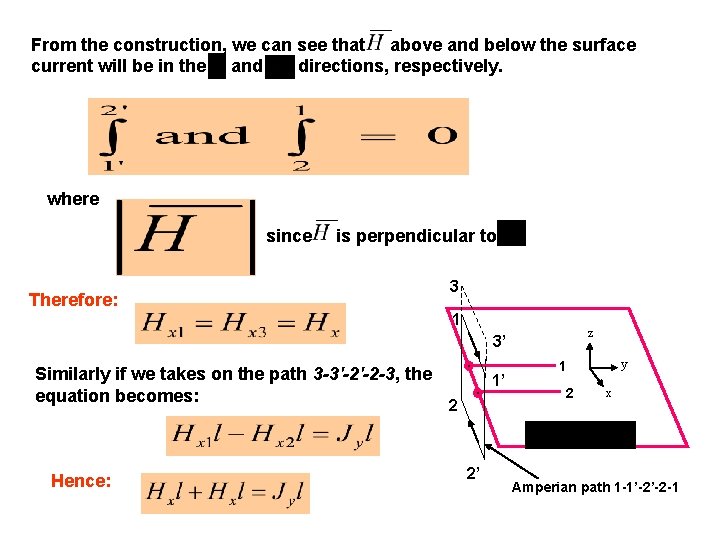
From the construction, we can see that above and below the surface current will be in the and directions, respectively. where since is perpendicular to Therefore: 3 1 z 3’ Similarly if we takes on the path 3 -3'-2'-2 -3, the equation becomes: Hence: 1’ 2 2’ y 1 2 x Amperian path 1 -1’-2’-2 -1

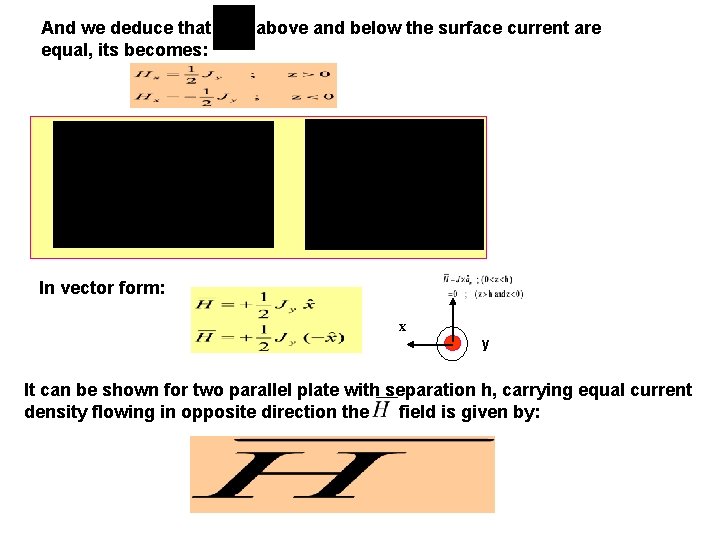
And we deduce that equal, its becomes: above and below the surface current are In vector form: x y It can be shown for two parallel plate with separation h, carrying equal current density flowing in opposite direction the field is given by:

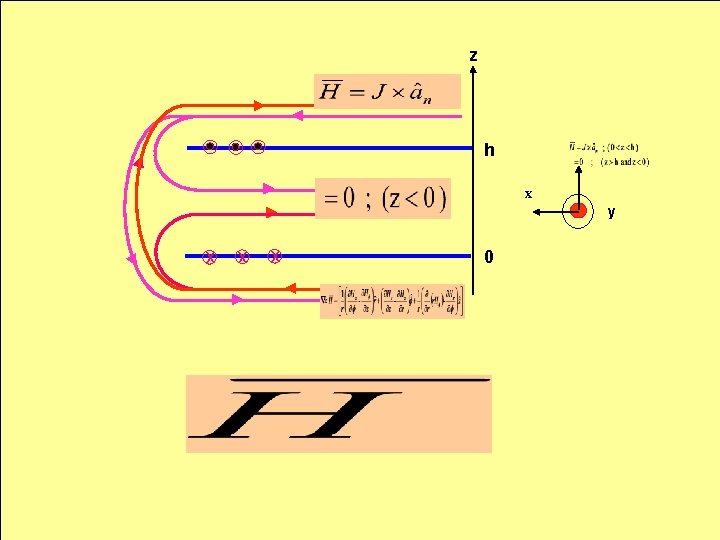
z h x y x x x 0

7. 5 CURL (IKAL) The curl of a vector field, is another vector field. For example in Cartesian coordinate, combining the three components, curl can be written as: And can be simplified as:

Expression for curl in cyclindrical and spherical coordinates: cyclindrical spherical

7. 5. 1 RELATIONSHIP OF H AND J Meaning that if will produce is known throughout a region, then for that region.

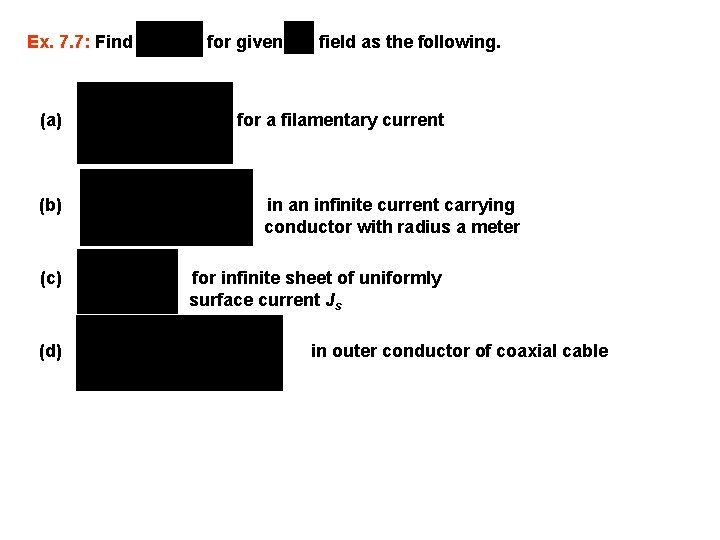
Ex. 7. 7: Find (a) (b) (c) (d) for given field as the following. for a filamentary current in an infinite current carrying conductor with radius a meter for infinite sheet of uniformly surface current Js in outer conductor of coaxial cable

Solution: (a) => Cyclindrical coordinate =0 Hence: =0 =0

Solution: (b) Cyclindrical coordinate =0 Hence: =0 =0

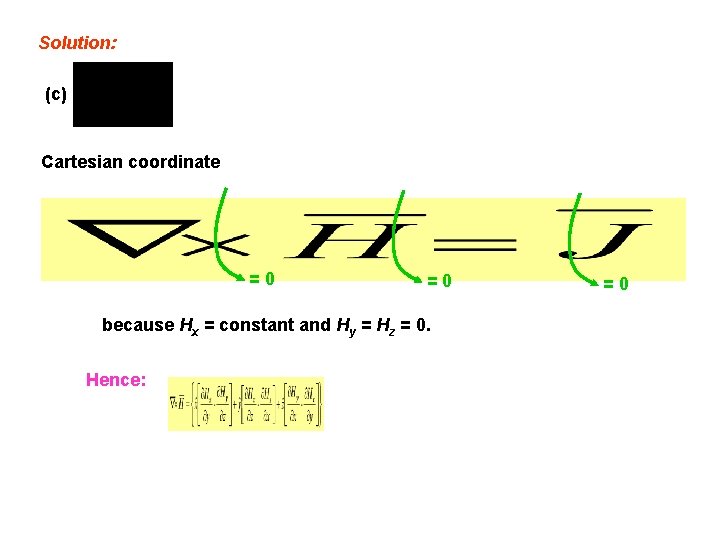
Solution: (c) Cartesian coordinate =0 =0 because Hx = constant and Hy = Hz = 0. Hence: =0

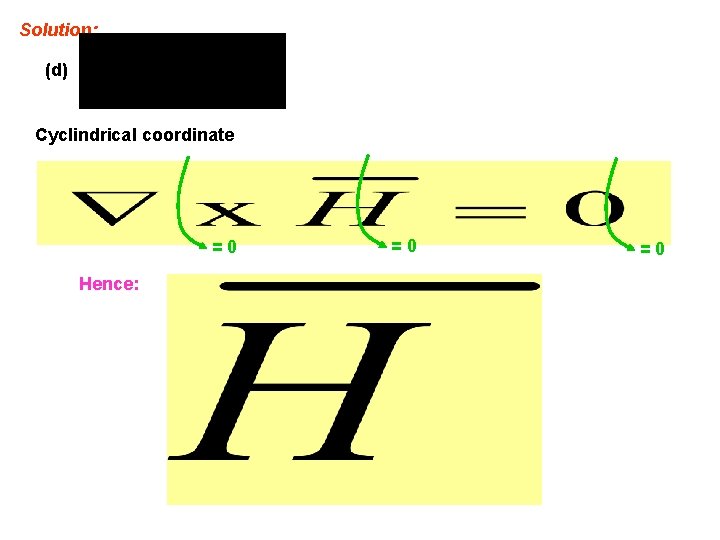
Solution: (d) Cyclindrical coordinate =0 Hence: =0 =0

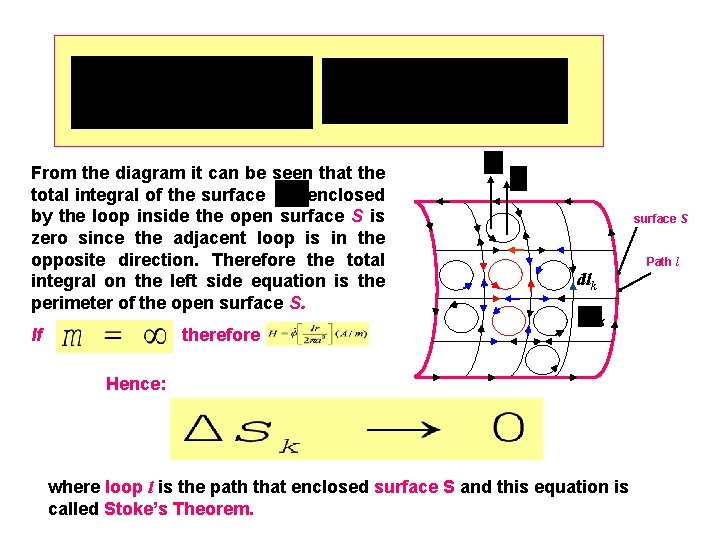
7. 6 STOKE’S THEOREM Stoke’s theorem states that the integral of the tangential component of a vector field around l is equal to the integral of the normal component of curl over S. In other word Stokes’s theorem relates closed loop line integral to the surface integral

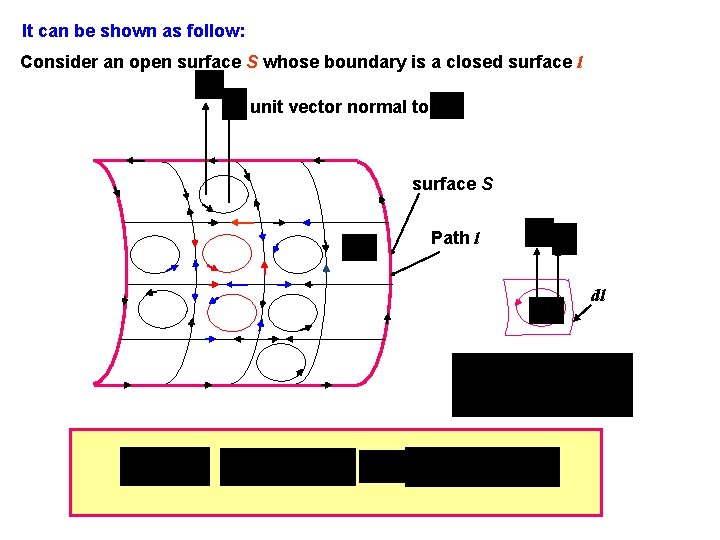
It can be shown as follow: Consider an open surface S whose boundary is a closed surface l unit vector normal to surface S Path l dl

From the diagram it can be seen that the total integral of the surface enclosed by the loop inside the open surface S is zero since the adjacent loop is in the opposite direction. Therefore the total integral on the left side equation is the perimeter of the open surface S. If therefore surface S Path l dlk k Hence: where loop l is the path that enclosed surface S and this equation is called Stoke’s Theorem.

Ex. 7. 8: was found in an infinite conductor of radius a meter. Evaluate both side of Stoke’s theorem to find the current flow in the conductor. Solution:

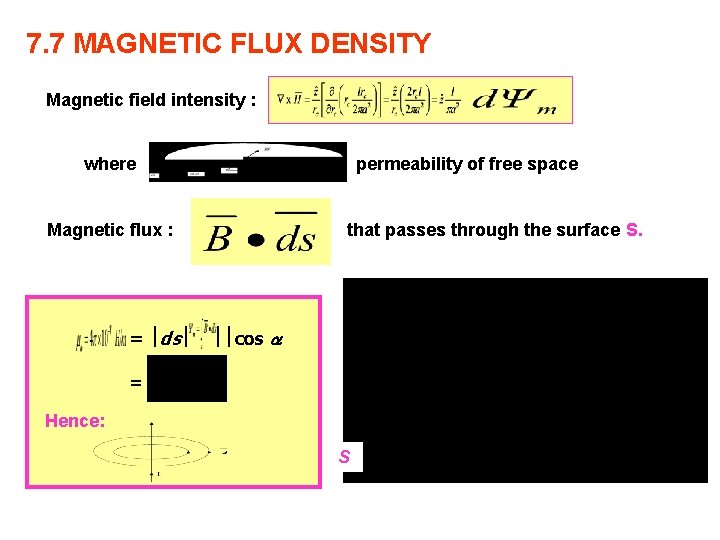
7. 7 MAGNETIC FLUX DENSITY Magnetic field intensity : where permeability of free space Magnetic flux : = ds that passes through the surface S. cos = Hence: S

In magnetics, magnet poles have not been isolated: 4 th. Maxwell’s equation for static fields.

Ex. 7. 9: For (Am-1), find the m that passes through a plane surface by, ( = /2), (2 r 4), and (0 z 2). Solution:

7. 8 MAXWELL’S EQUATIONS POINT FORM INTEGRAL FORM Electrostatic fields : Magnetostatic fields:

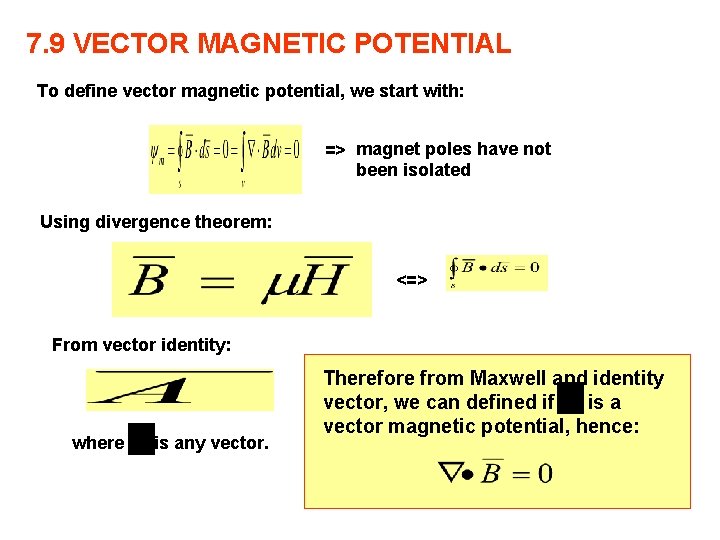
7. 9 VECTOR MAGNETIC POTENTIAL To define vector magnetic potential, we start with: => magnet poles have not been isolated Using divergence theorem: <=> From vector identity: where is any vector. Therefore from Maxwell and identity vector, we can defined if is a vector magnetic potential, hence:

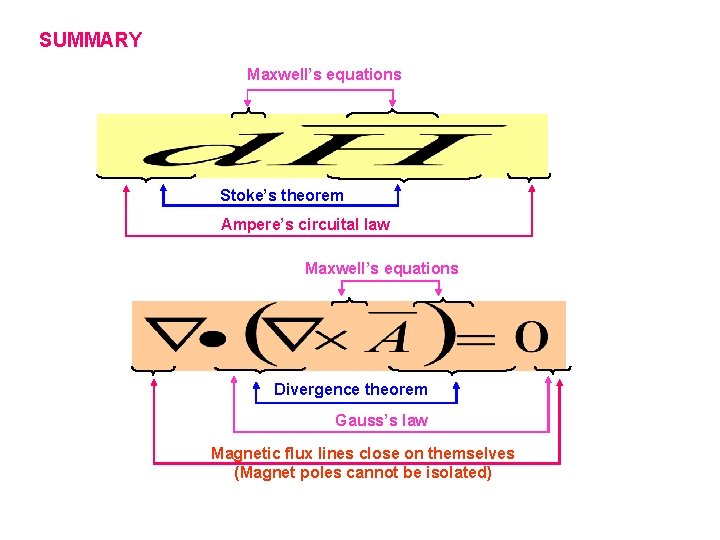
SUMMARY Maxwell’s equations Stoke’s theorem Ampere’s circuital law Maxwell’s equations Divergence theorem Gauss’s law Magnetic flux lines close on themselves (Magnet poles cannot be isolated)