Chapter 5 Applications of Integration Areas Volumes Work

Chapter 5. Applications of Integration Areas, Volumes, Work Sections 5. 1, 5. 2, 5. 3, 5. 4

5. 1 Area between curves

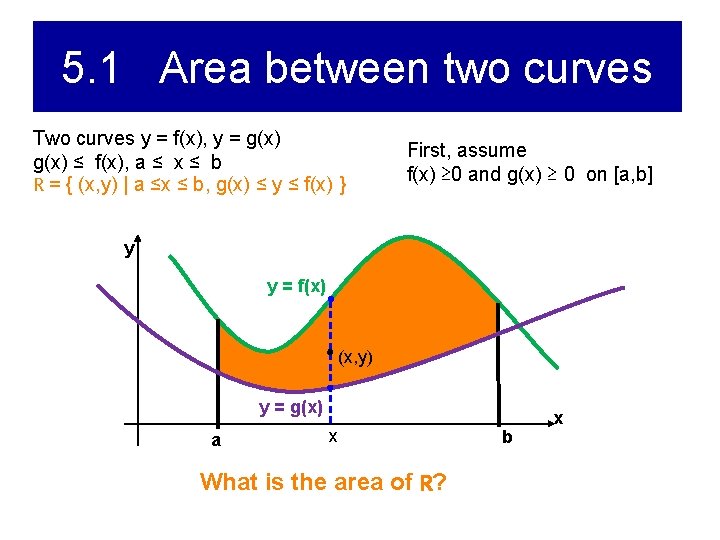
5. 1 Area between two curves Two curves y = f(x), y = g(x) ≤ f(x), a ≤ x ≤ b R = { (x, y) | a ≤x ≤ b, g(x) ≤ y ≤ f(x) } First, assume f(x) ≥ 0 and g(x) ≥ 0 on [a, b] y y = f(x) (x, y) y = g(x) a x What is the area of R? b x

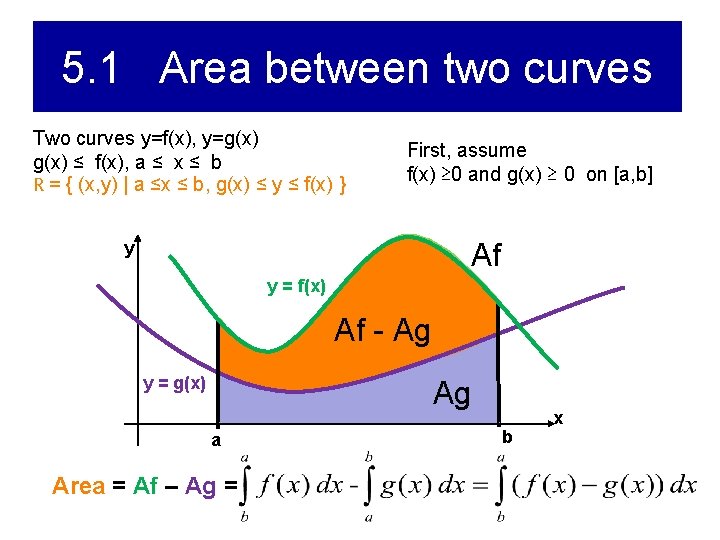
5. 1 Area between two curves Two curves y=f(x), y=g(x) ≤ f(x), a ≤ x ≤ b R = { (x, y) | a ≤x ≤ b, g(x) ≤ y ≤ f(x) } First, assume f(x) ≥ 0 and g(x) ≥ 0 on [a, b] Af y y = f(x) Af - Ag y = g(x) a Area = Af – Ag = Ag b x

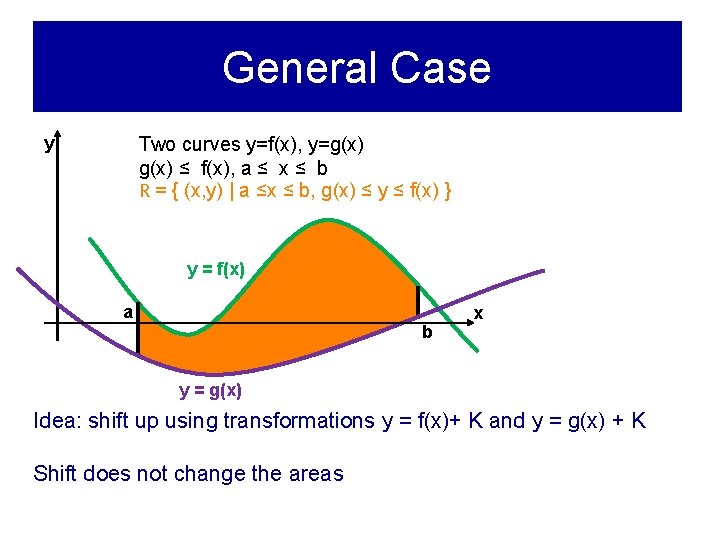
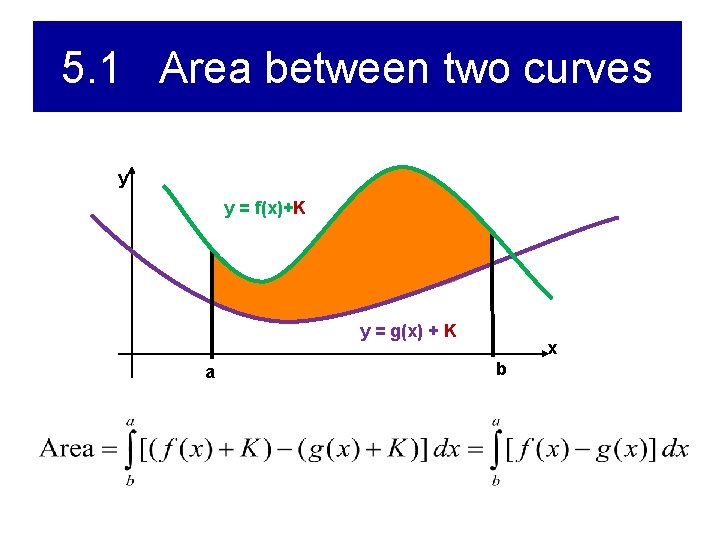
General Case y Two curves y=f(x), y=g(x) ≤ f(x), a ≤ x ≤ b R = { (x, y) | a ≤x ≤ b, g(x) ≤ y ≤ f(x) } y = f(x) a b x y = g(x) Idea: shift up using transformations y = f(x)+ K and y = g(x) + K Shift does not change the areas

5. 1 Area between two curves y y = f(x)+K y = g(x) + K a x b

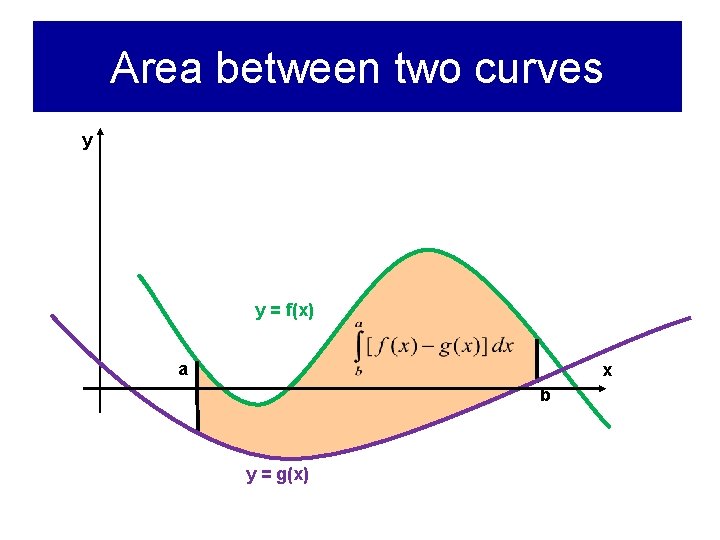
Area between two curves y y = f(x) a x b y = g(x)

Intersections of graphs • Often, a or both correspond to points where graphs y = f(x) and y = g(x) intersect • To find intersection points, solve equation f(x) = g(x)

5. 2 Volumes

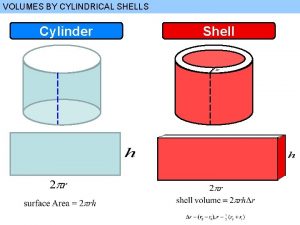
Volumes of simple 3 D objects h h V = (L W) h V = (π r 2) h r L W In both cases, V = A h = (Area of the base) (height)

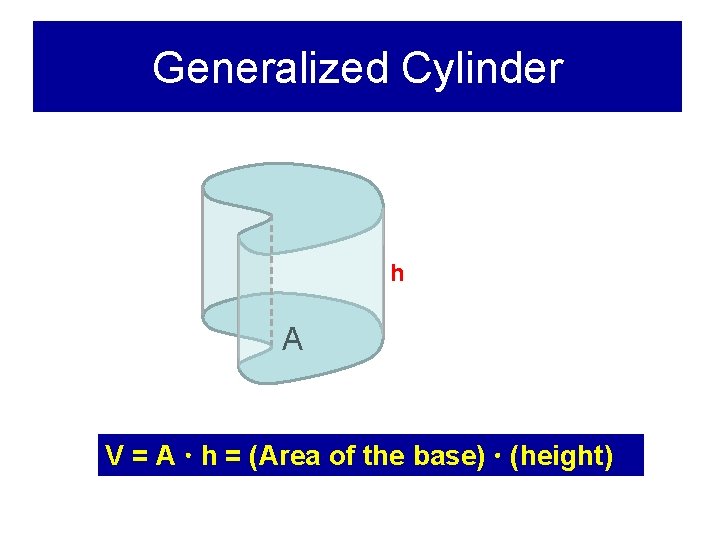
Generalized Cylinder h A V = A h = (Area of the base) (height)

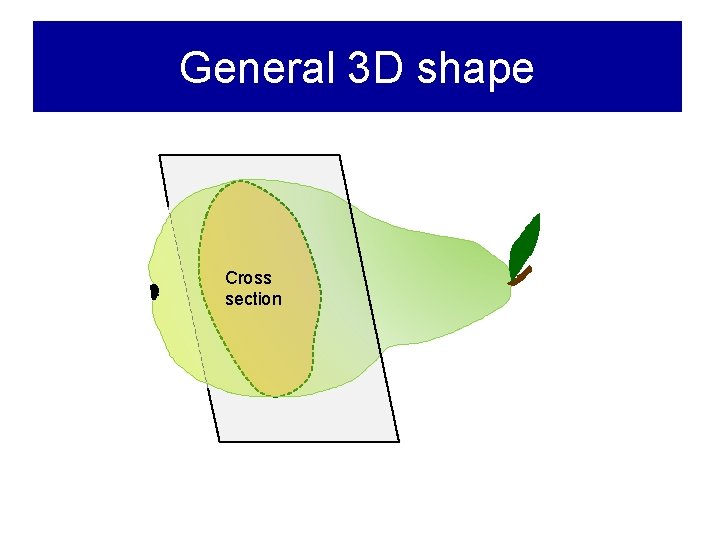
General 3 D shape Cross section

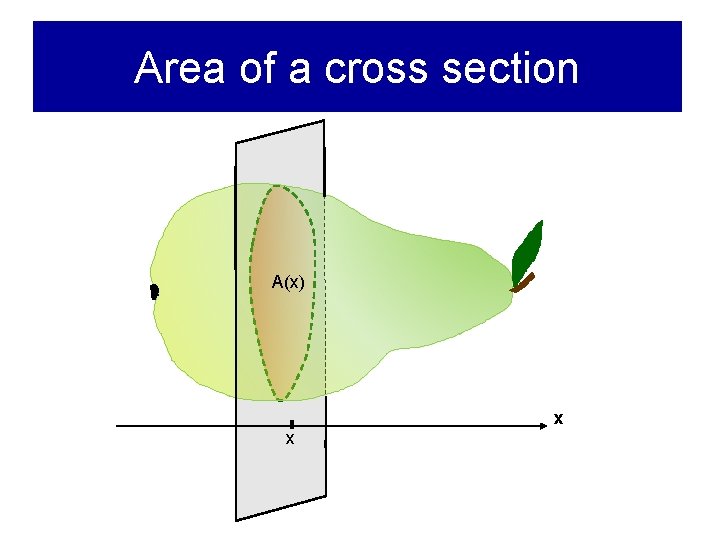
Area of a cross section A(x) x x

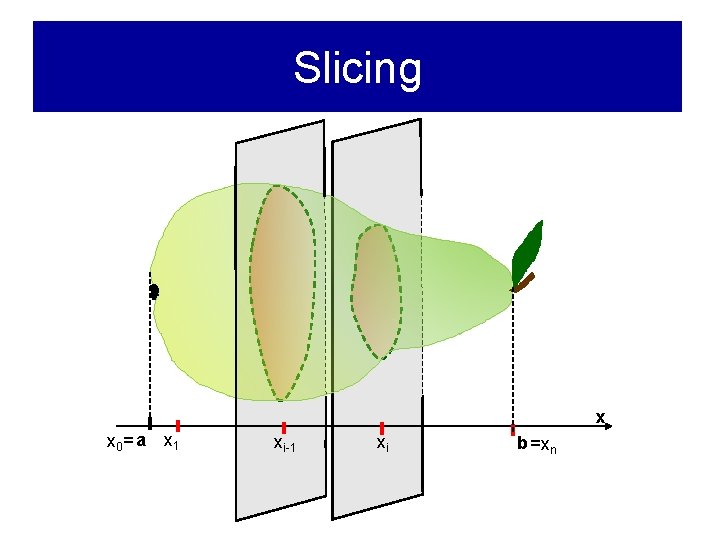
Slicing x x 0= a x 1 xi-1 xi b =xn

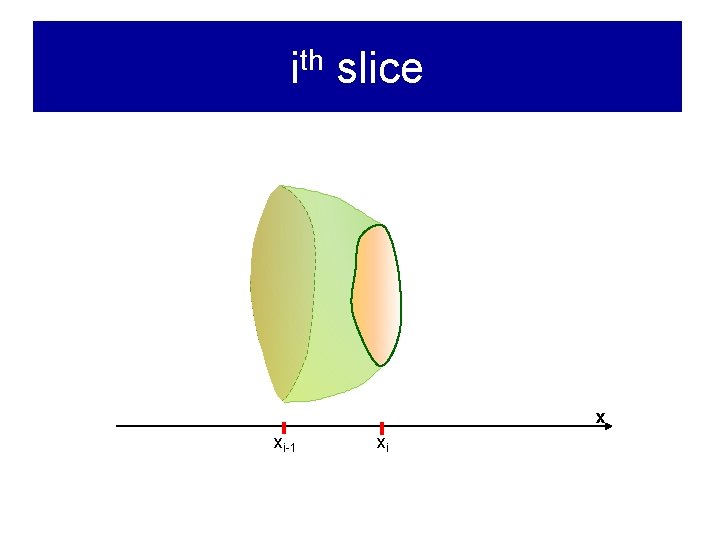
ith slice x xi-1 xi

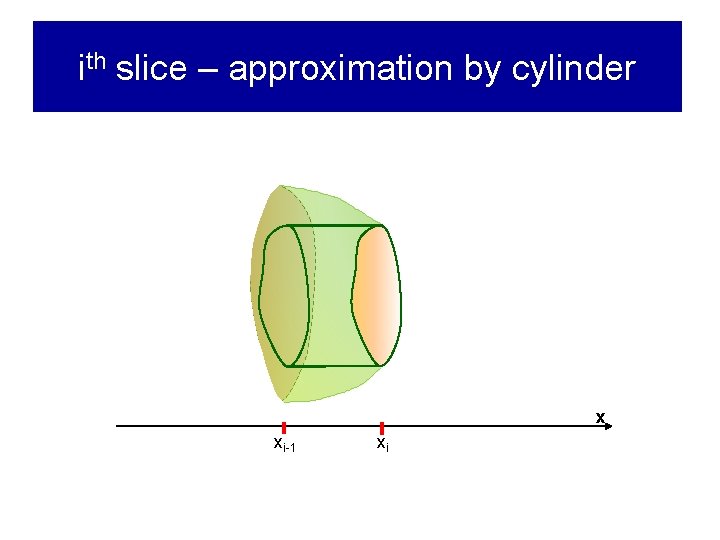
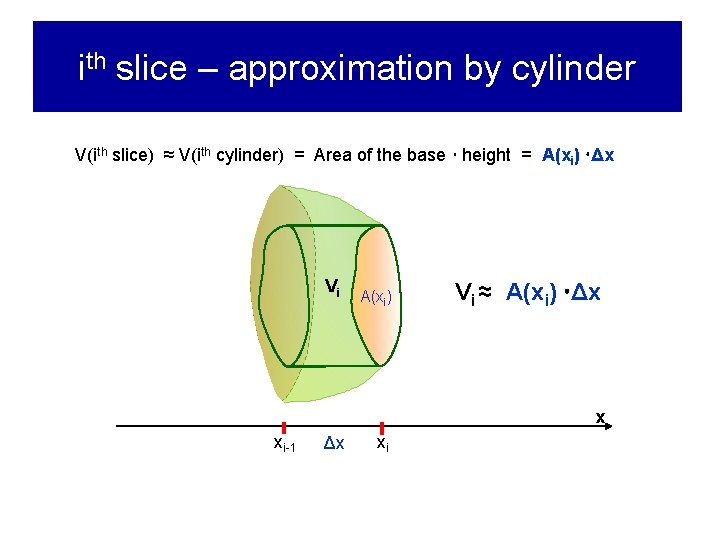
ith slice – approximation by cylinder x xi-1 xi

ith slice – approximation by cylinder V(ith slice) ≈ V(ith cylinder) = Area of the base height = A(xi) Δx Vi A(xi) Vi ≈ A(xi) Δx x xi-1 Δx xi

Total Volume Total volume = sum of volumes of all slices ≈ sum of volumes of all approximating cylinders

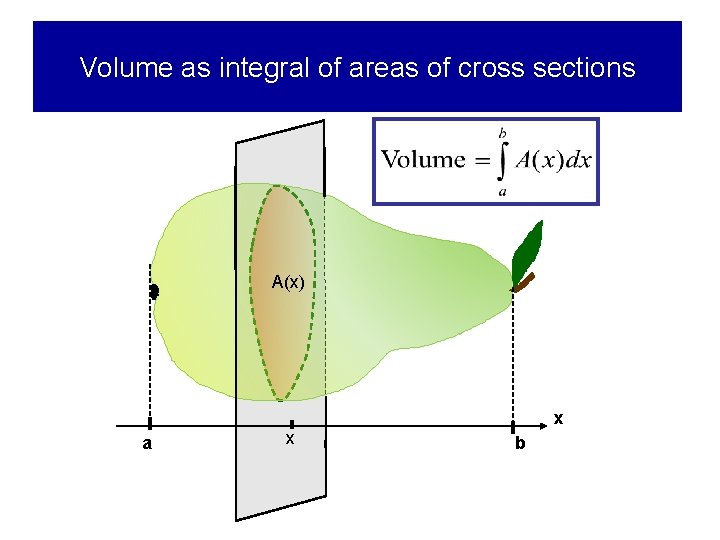
Volume as integral of areas of cross sections A(x) x a x b

Solids of revolution

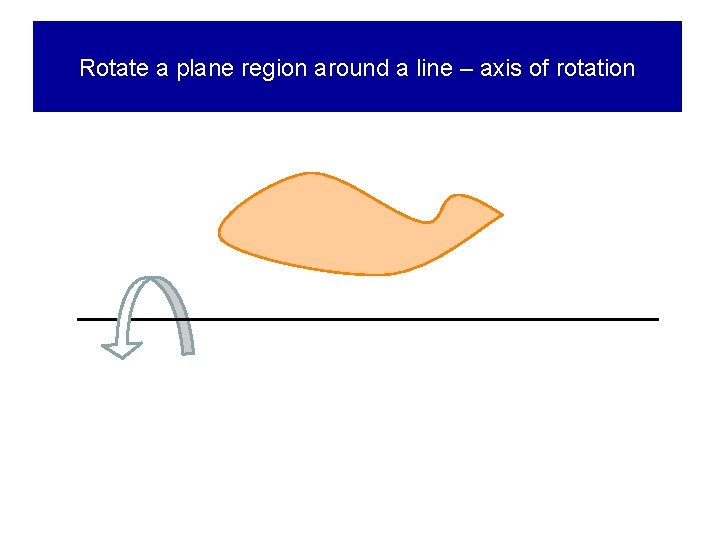
Rotate a plane region around a line – axis of rotation

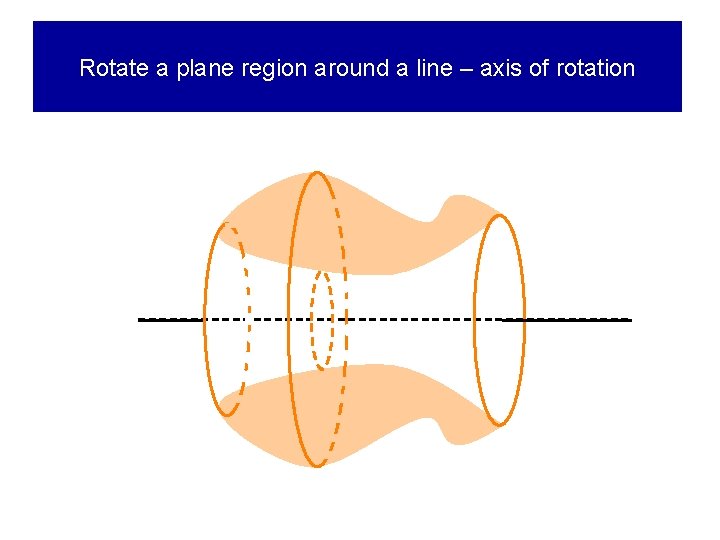
Rotate a plane region around a line – axis of rotation

Volumes of solids of revolution using “washers”

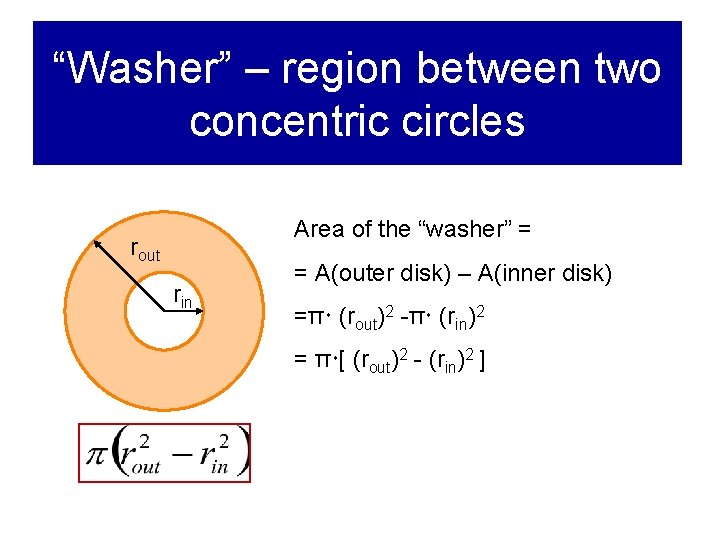
“Washer” – region between two concentric circles Area of the “washer” = rout rin = A(outer disk) – A(inner disk) =π (rout)2 -π (rin)2 = π [ (rout)2 - (rin)2 ]

Cross sections are washers

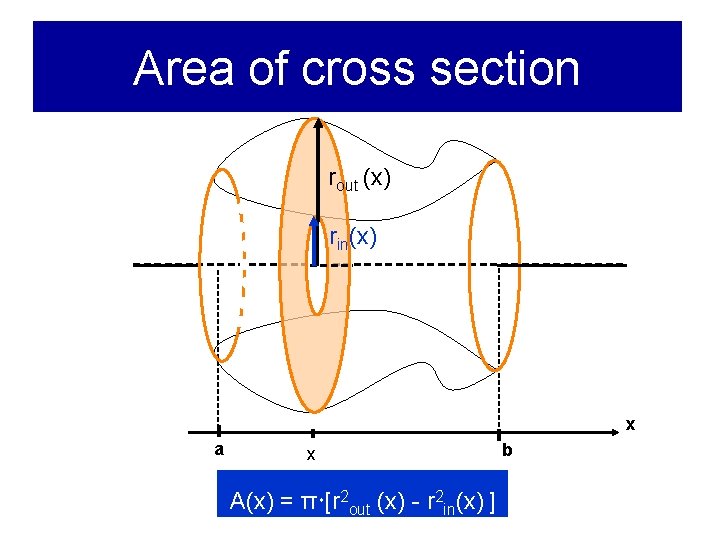
Area of cross section rout (x) rin(x) x a x A(x) = π [r 2 out (x) - r 2 in(x) ] b

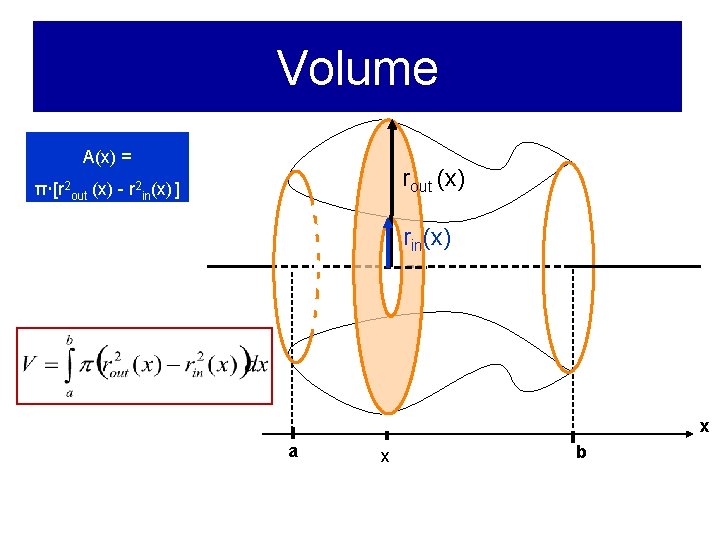
Volume A(x) = rout (x) π [r 2 out (x) - r 2 in(x) ] rin(x) x a x b