Chapter 2 Kinematics in One Dimension Ch 2

Chapter 2 Kinematics in One Dimension Ch 2 Giancoli, PHYSICS, 6/E © 2004. Electronically reproduced by permission of Pearson Education, Inc. , Upper Saddle River, New Jersey 1

Module 2 Displacement, Velocity and Acceleration Giancoli, Sec 2 -1, 2, 3, 4, 8 The following is an excellent lecture on this material. AP Physics C Lesson 1 Ch 2 Giancoli, PHYSICS, 6/E © 2004. Electronically reproduced by permission of Pearson Education, Inc. , Upper Saddle River, New Jersey 2

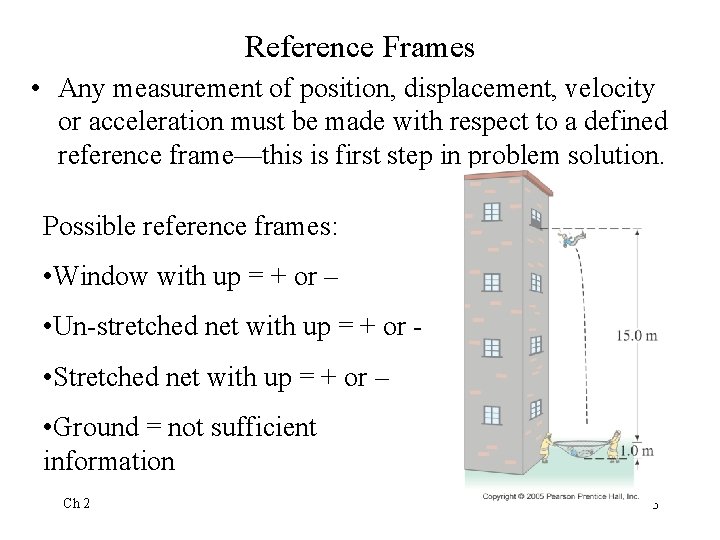
Reference Frames • Any measurement of position, displacement, velocity or acceleration must be made with respect to a defined reference frame—this is first step in problem solution. Possible reference frames: • Window with up = + or – • Un-stretched net with up = + or • Stretched net with up = + or – • Ground = not sufficient information Ch 2 3

Coordinate Axis • We will use a set of coordinate axis where x is horizontal and y is vertical +y -x x 1 x 2 +x -y • Many problems will be motion in one dimension so we will plot x vs. time. Ch 2 4

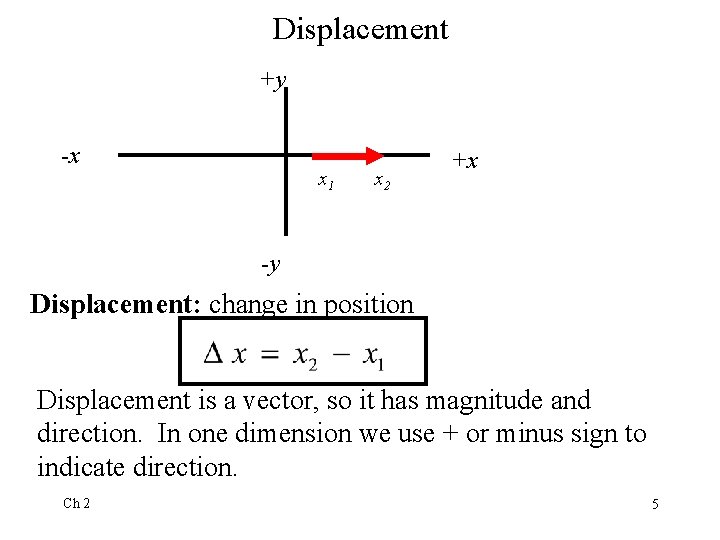
Displacement +y -x x 1 x 2 +x -y Displacement: change in position Displacement is a vector, so it has magnitude and direction. In one dimension we use + or minus sign to indicate direction. Ch 2 5

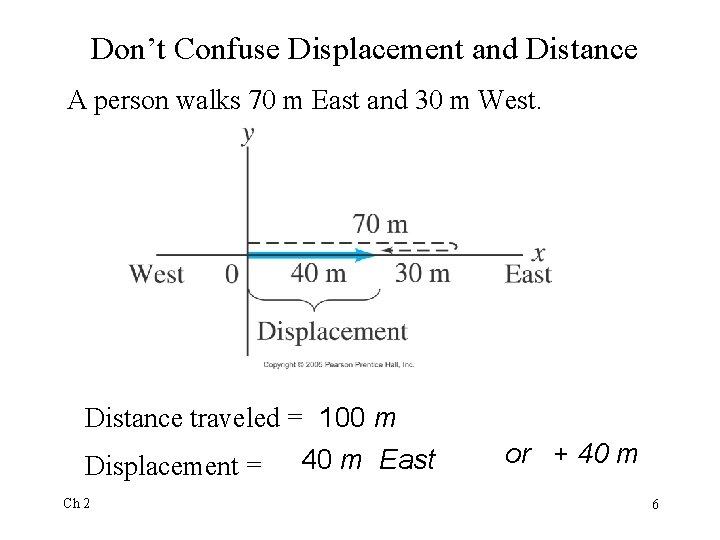
Don’t Confuse Displacement and Distance A person walks 70 m East and 30 m West. Distance traveled = 100 m Displacement = 40 m East Ch 2 or + 40 m 6

Negative Displacement In the figure below the displacement is negative. A negative displacement may indicate motion toward the West or something else depending on the situation and the coordinate system chosen. Ch 2 7

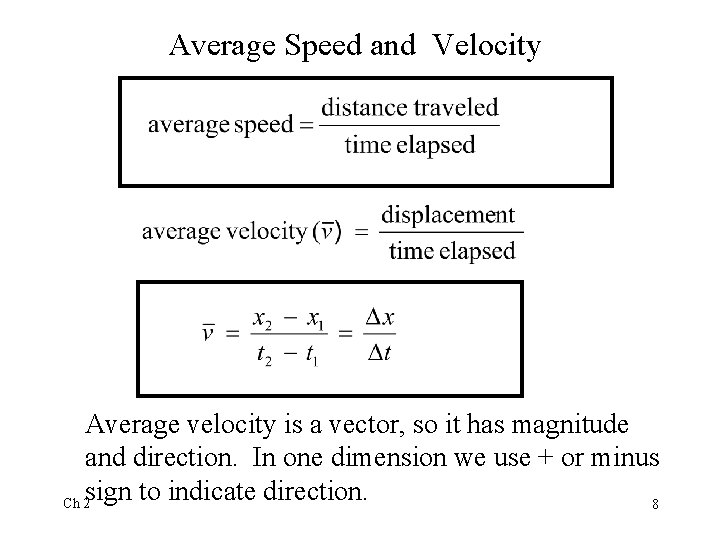
Average Speed and Velocity Average velocity is a vector, so it has magnitude and direction. In one dimension we use + or minus sign to indicate direction. Ch 2 8

Example 1. An airplane travels 3100 km at a speed of 790 km/h, and then encounters a tailwind that boosts its speed to 990 km/h for the next 2800 km. What was the total time for the trip? (Assume three significant figures) Ch 2 9

Example 1 (continued) An airplane travels 3100 km at a speed of 790 km/h, and then encounters a tailwind that boosts its speed to 990 km/h for the next 2800 km. What was the total time for the trip? (Assume three significant figures) What was the average speed of the plane for this trip? Note: A simple average of v 1 and v 2 gives 890 km/h and is not correct Ch 2 10

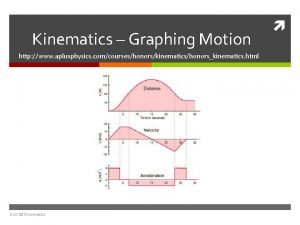
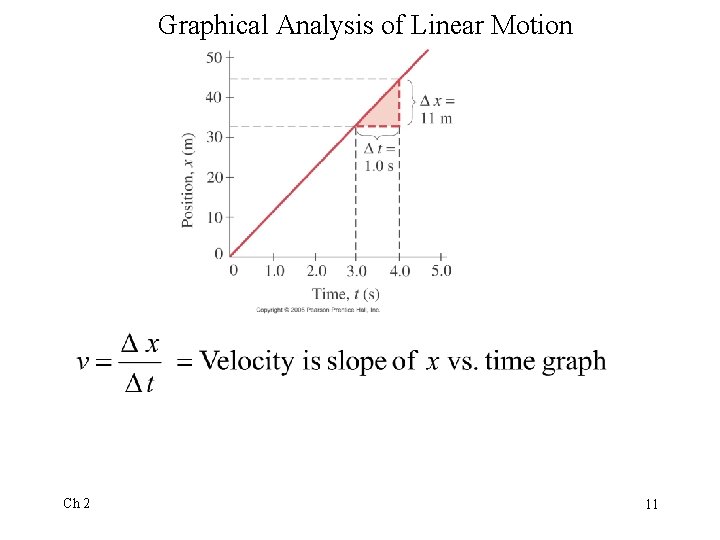
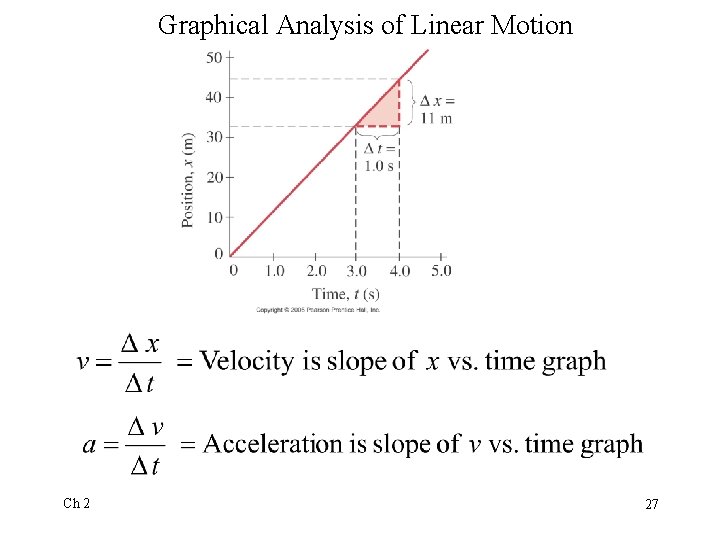
Graphical Analysis of Linear Motion Ch 2 11

Acceleration Average Acceleration: change in velocity divided by the time taken to make this change. Ch 2 12

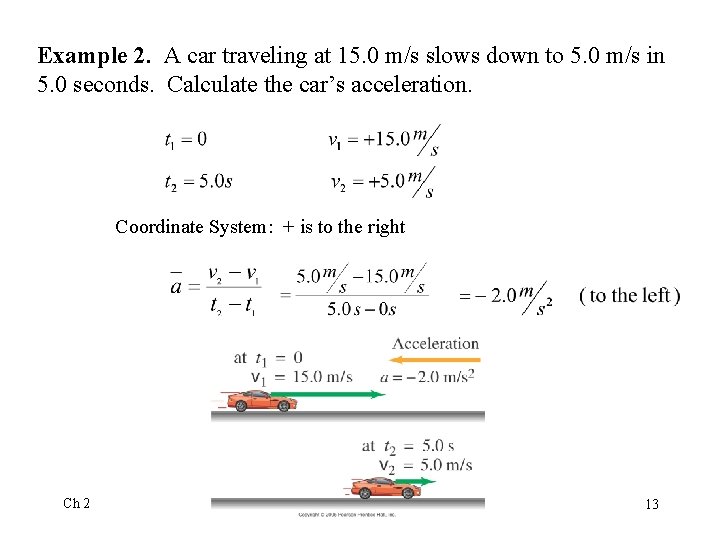
Example 2. A car traveling at 15. 0 m/s slows down to 5. 0 m/s in 5. 0 seconds. Calculate the car’s acceleration. Coordinate System: + is to the right Ch 2 13

Acceleration Instantaneous Acceleration: same definition as before but over a very short t. Ch 2 14

Instantaneous Velocity instantaneous velocity is defined as the average velocity over an infinitesimally short time interval. Ch 2 15

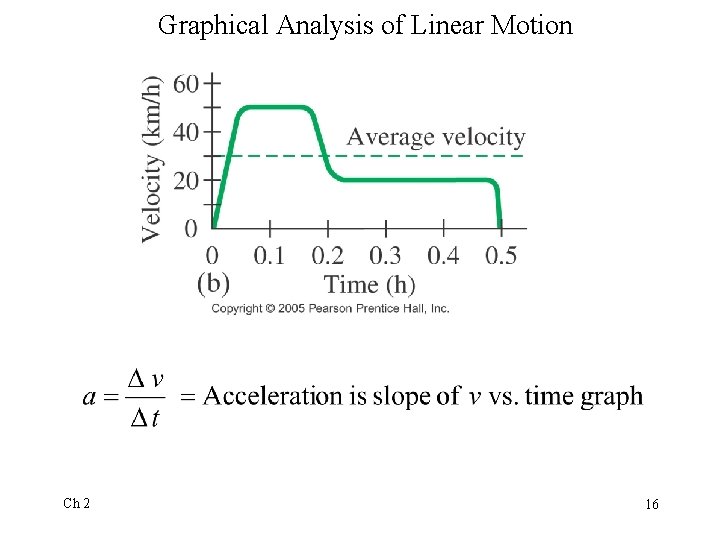
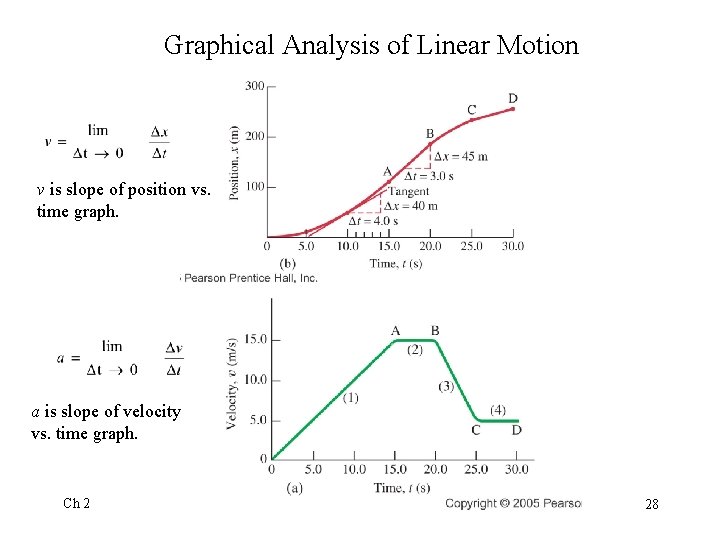
Graphical Analysis of Linear Motion Ch 2 16

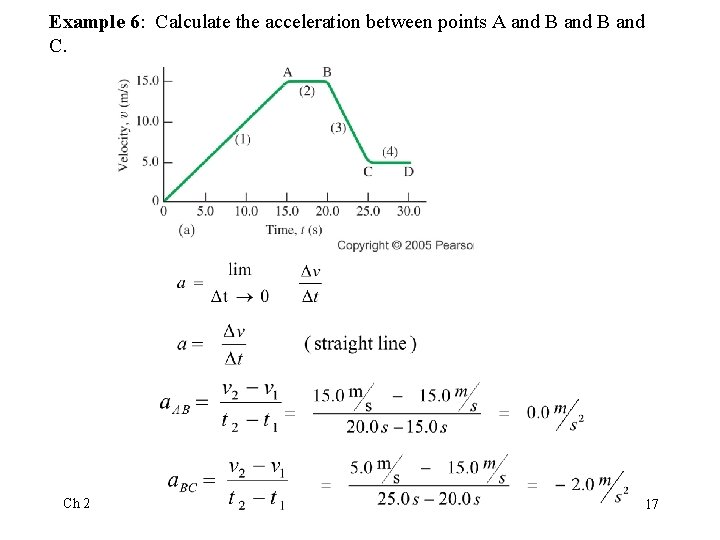
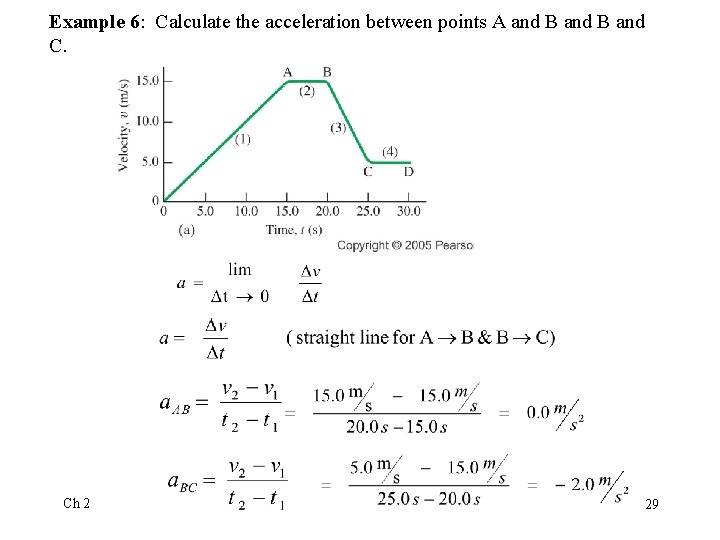
Example 6: Calculate the acceleration between points A and B and C. Ch 2 17

Module 3 Motion with Constant Acceleration Giancoli, Sec 2 -1, 2, 3, 4, 8 Ch 2 Giancoli, PHYSICS, 6/E © 2004. Electronically reproduced by permission of Pearson Education, Inc. , Upper Saddle River, New Jersey 18

Motion with Constant Acceleration Consider the case of a car that accelerates from rest with a constant acceleration of 15 m / s 2. We can make a table Ch 2 t (s) v ( m/s) a ( m/ s 2 ) 0 0 15 15 2 30 15 3 45 15 4 60 15 5 75 15 19

Derivations • In the next 4 slides we will combine several known equations under the assumption that the acceleration is constant. • This process is called a derivation. • In general you will need to know the initial assumptions, the resultant equations and how to apply them. • You do not need to memorize derivations • But, I could ask you to derive an equation for a specific problem. This is very similar to an ordinary problem without a numeric answer. Ch 2 20

Motion at Constant Acceleration - Derivation • Consider the special case acceleration equals a constant: a = constant • Use the subscript “ 0” to refer to the initial conditions • Thus t 0 refers to the initial time and we will set t 0 = 0. • At this time v 0 is the initial velocity and x 0 is the initial displacement. • At a later time t, v is the velocity and x is the displacement • In the equations t 1 t 0 and t 2 t Ch 2 21

Motion at Constant Acceleration - Derivation The average velocity during this time is: The acceleration is assumed to be constant From this we can write Ch 2 22

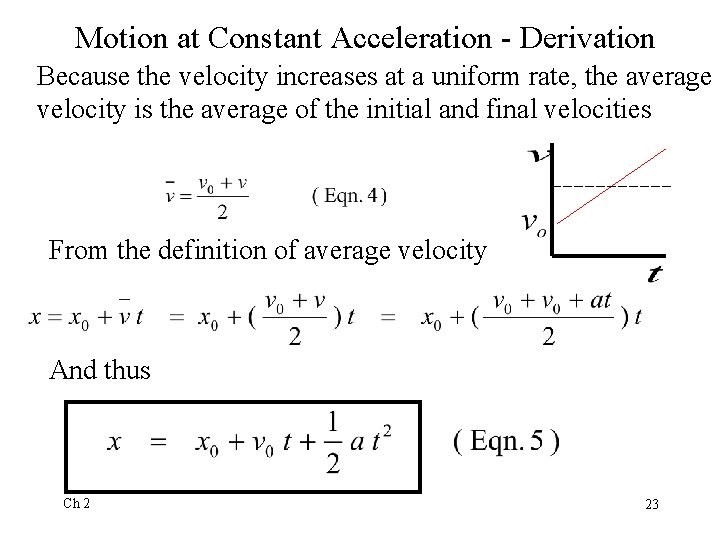
Motion at Constant Acceleration - Derivation Because the velocity increases at a uniform rate, the average velocity is the average of the initial and final velocities From the definition of average velocity And thus Ch 2 23

Motion at Constant Acceleration • The book derives one more equation by eliminating time • The 4 equations listed below only apply when = constant Ch 2 a 24

Example 3. A world-class sprinter can burst out of the blocks to essentially top speed (of about 11. 5 m/s) in the first 15. 0 m of the race. What is the average acceleration of this sprinter, and how long does it take her to reach that speed? (Note: we have to assume a=constant) Ch 2 25

Example 4. A truck going at a constant speed of 25 m/s passes a car at rest. The instant the truck passes the car, the car begins to accelerate at a constant 1. 00 m / s 2. How long does it take for the car to catch up with the truck. When the car catches the truck: How far has the car traveled when it catches the truck? Ch 2 26

Graphical Analysis of Linear Motion Ch 2 27

Graphical Analysis of Linear Motion v is slope of position vs. time graph. a is slope of velocity vs. time graph. Ch 2 28

Example 6: Calculate the acceleration between points A and B and C. Ch 2 29

Module 4 Falling Objects Giancoli, Sec 2 -1, 2, 3, 4, 8 Ch 2 Giancoli, PHYSICS, 6/E © 2004. Electronically reproduced by permission of Pearson Education, Inc. , Upper Saddle River, New Jersey 30

Falling Objects • Galileo showed that for object falling from rest with no air resistance y t 2 • Note that this is true when acceleration is constant Ch 2 31

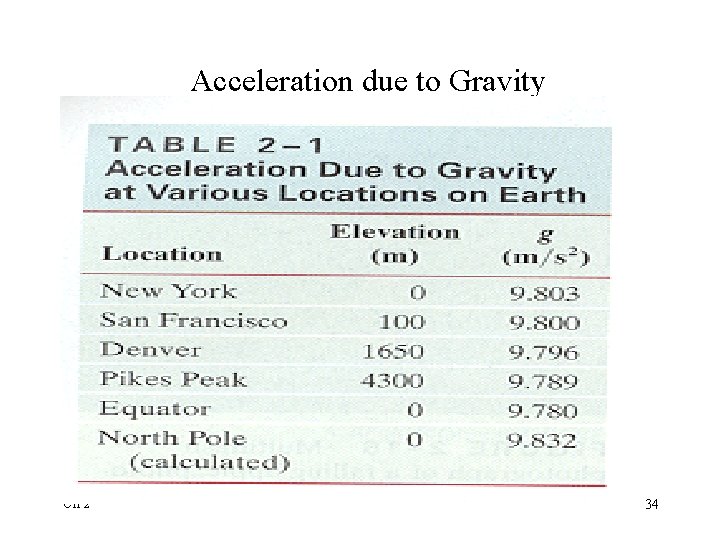
Falling Objects Galilei showed that • near the surface of the earth • at the same location • in the absence of air resistance all objects fall with the same constant acceleration g, the acceleration due to gravity g = 9. 8 m/s 2 Note: g is a positive number. When you define your coordinate system, you can decide whether up or down is positive. Ch 2 32

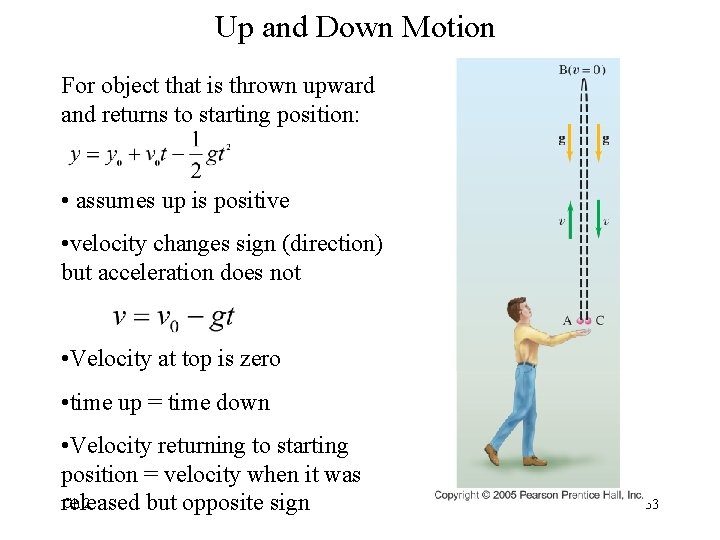
Up and Down Motion For object that is thrown upward and returns to starting position: • assumes up is positive • velocity changes sign (direction) but acceleration does not • Velocity at top is zero • time up = time down • Velocity returning to starting position = velocity when it was Ch 2 released but opposite sign 33

Acceleration due to Gravity Ch 2 34

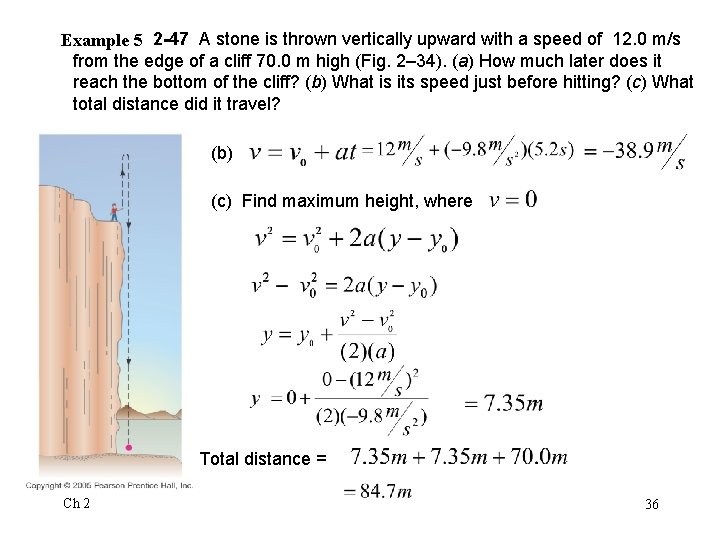
Example 5 (2 -47) A stone is thrown vertically upward with a speed of 12. 0 m/s from the edge of a cliff 70. 0 m high (Fig. 2– 34). (a) How much later does it reach the bottom of the cliff? (b) What is its speed just before hitting? (c) What total distance did it travel? (a) UP = POSITIVE Use quadratic equation: Answer = 5. 20 s Ch 2 35

Example 5 2 -47 A stone is thrown vertically upward with a speed of 12. 0 m/s from the edge of a cliff 70. 0 m high (Fig. 2– 34). (a) How much later does it reach the bottom of the cliff? (b) What is its speed just before hitting? (c) What total distance did it travel? (b) (c) Find maximum height, where Total distance = Ch 2 36

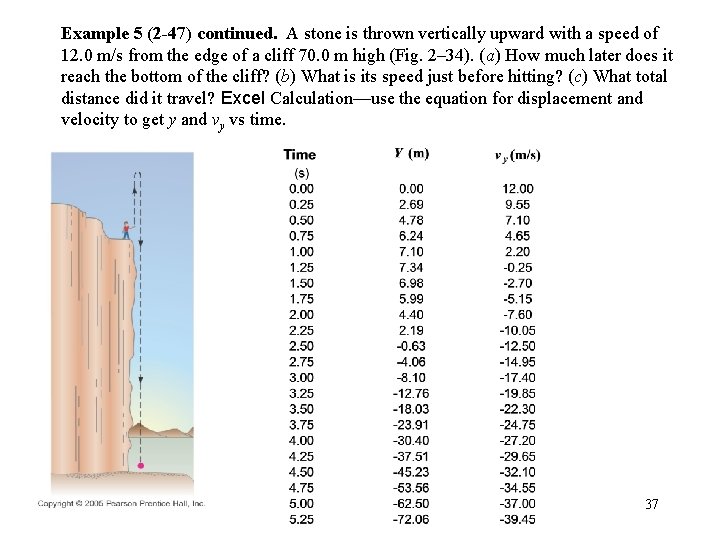
Example 5 (2 -47) continued. A stone is thrown vertically upward with a speed of 12. 0 m/s from the edge of a cliff 70. 0 m high (Fig. 2– 34). (a) How much later does it reach the bottom of the cliff? (b) What is its speed just before hitting? (c) What total distance did it travel? Excel Calculation—use the equation for displacement and velocity to get y and vy vs time. Ch 2 37

Problem Solving Tips 1. Read the whole problem and make sure you understand it. Then read it again. 2. Decide on the objects under study and what the time interval is. 3. Draw a diagram and choose coordinate axes. 4. Write down the known (given) quantities, and then the unknown ones that you need to find. 5. What physics applies here? Plan an approach to a solution. Ch 2 38

Problem Solving Tips 6. Which equations relate the known and unknown quantities? Are they valid in this situation? Solve algebraically for the unknown quantities, and check that your result is sensible (correct dimensions). 7. Calculate the solution and round it to the appropriate number of significant figures. 8. Look at the result – is it reasonable? Does it agree with a rough estimate? 9. Check the units again. Ch 2 39