CHAP 0 MATHEMATICAL PRELIMINARY FINITE ELEMENT ANALYSIS AND

CHAP 0 MATHEMATICAL PRELIMINARY FINITE ELEMENT ANALYSIS AND DESIGN Nam-Ho Kim 1

MATHEMATICAL PRELIMINARY • Vector – a collection of scalars, defined using a bold typeface with braces • Matrix – a collection of vectors, defined using a bold typeface with brackets – dimension = N×K. When N = K, it is called a square matrix 2

MATRIX – Transpose of a matrix: Change of row and column – Symmetric and Skew-symmetric matrices – Identity matrix 3

VECTOR-MATRIX CALCULUS • Addition • Scalar product between two vectors (must be the same dim) • Norm (Magnitude of a vector) 4

DETERMINANT • • • Similar to the norm of a vector Only defined for a square matrix If a determinant is zero, the matrix is not invertible A matrix is singular when its determinant is zero For a 2 x 2 matrix: • For a 3 x 3 matrix 5

VECTOR-MATRIX CALCULUS cont. • Vector product – Scalar product result = scalar – Vector product result = vector 6

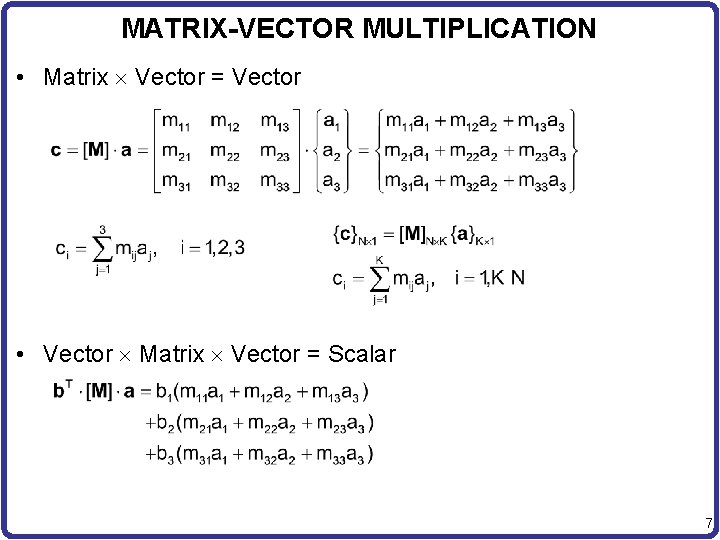
MATRIX-VECTOR MULTIPLICATION • Matrix Vector = Vector • Vector Matrix Vector = Scalar 7

MATRIX-MATRIX MULTIPLICATION • Matrix = Matrix • Inverse of a matrix: – A square matrix [A] is invertible, then – If a matrix is singular (|A| = 0), then the inverse does not exist 8

RULES OF MATRIX MULTIPLICATION • Associative rule: • Distributive rule: • Non-commutative: • Transpose of product: • Inverse of product: 9

MATRIX EQUATION – N unknowns (x 1, x 2, …, x. N) and N equations – unique solution if all equations are independent – Matrix form: – Solution: [A]– 1 exists or [A] is not singular 10

EIGEN VALUE AND EIGEN VECTOR • Eigen value problem : Eigen value : Eigen vector • How to solve? – {x} = {0} is a solution (trivial solution) – In order to have non-trivial solution, the determinant must be zero. – Calculate problem from this equation and calculate from the eigen value 11

EIGEN VALUE AND EIGEN VECTOR • Characteristic equation – The textbook has a solution for [A]3 x 3 case • Eigen vectors – After solving for eigen values, substitute each of them to eigen problem – Since is singular, no unique solution exists – Practice example in the textbook 12

QUADRATIC FORM • Quadratic form: quadratic function of all components • Matrix notation • Symmetric part is enough ([B] is not sym) 13

POSITIVE DEFINITE MATRIX • Positive definite • Positive semi-definite • Positive definiteness = each column of the matrix is linearly independent = the matrix is invertible = the matrix is not singular = the matrix equation has a unique solution. 14

MAXIMA & MINIMA OF FUNCTIONS • Single Variable f(x) – Taylor series expansion – In order for f to be extremum, – Condition for minima: – Condition for maxima: 15

MAXIMA & MINIMA OF FUNCTIONS cont. • Multi-Variable f(x) – Taylor series expansion – In order for f to be extremum, Hessian matrix Hij – Condition for minima: [H] is positive definite – Condition for maxima: [H] is negative definite 16

MINIMUM PRINCIPLE • Function in quadratic form – [A]: stiffness of the structure, {x}: displacement, {b}: applied force – Potential energy – structure is in equilibrium when F has a minimum value • Matrix equation – Solution of the matrix equation minimizes the quadratic form F. 17

Homework #1 5. For the two matrices [A] and [B] in Problem 2, answer the following questions. (a) Evaluate the matrix–matrix multiplication [C] = [A][B]. (b) Evaluate the matrix–matrix multiplication [D] = [B][A]. 7. Calculate the inverse of the matrix 9. Solve the following simultaneous system of equations using the matrix method: 18

Homework #1 11. Find the eigen values and eigen vectors 14. A function f(x 1, x 2) of two variables x 1 and x 2 is given by (a) Multiply the matrices and express f as a polynomial in x 1 and x 2. (b) Determine the extreme (maximum or minimum) value of the function and corresponding x 1 and x 2. (c) Is this a maxima or minima? 19