BEST RESPONSE MECHANISMS Noam Nisan Michael Schapira Gregory

BEST RESPONSE MECHANISMS Noam Nisan, Michael Schapira, Gregory Valiant, and Aviv Zohar

Motivation � Equilibrium is the basic object of study in game theory. � Question: How is an equilibrium reached? � In a truly satisfactory answer each player’s rule of behavior is simple and “locally rational” �repeated best-response �repeated better-response �regret-minimization

Motivation � Repeated best-response is often employed in practice �e. g. , Internet routing � We ask: “When is such locally-rational behavior really rational? ”

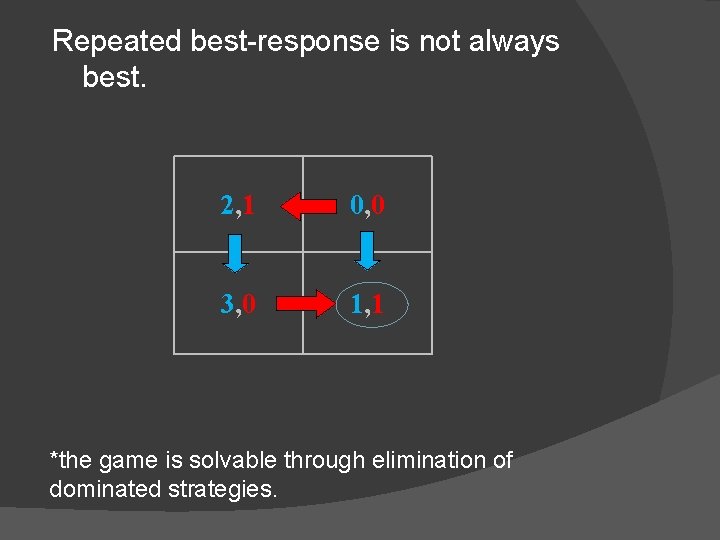
Repeated best-response is not always best. 2, 1 0, 0 3, 0 1, 1 *the game is solvable through elimination of dominated strategies.

Overview of Results We identify a small class of games for which: 1. Repeated best-response converges (quickly) from any initial point. 2. It is a rational choice in the long run (an equilibrium). While small, this class covers several important examples: Internet Routing, Cost Sharing, Stable Roommates, Congestion Control.

The Setting �

The repeated best-response strategy: When a player’s turn arrives, it announces the best response to the latest announcements of others.

Tie Breaking Rules �

Never Best Response (NBR) Strategies � 2 -20 0 -15 3 -3 3 -1 1 2 1

NBR-Solvability Def: A game G is NBR-solvable (under some tiebreaking rule) if there exists a sequence of eliminations of NBR strategies from the game that leaves each player with only a single strategy. There must be such a sequence for every type configuration of the players.

Clear Outcomes �

Example: Congestion Control � A crude model of TCP congestion control. [Godfrey, Schapira, Zohar, Shenker – SIGMETRICS 2010] � A protocol responsible for scaling back transmission rate in cases of congestion. � The network is represented by a graph with capacities on the edges. 3 3 2 4 1 2 1

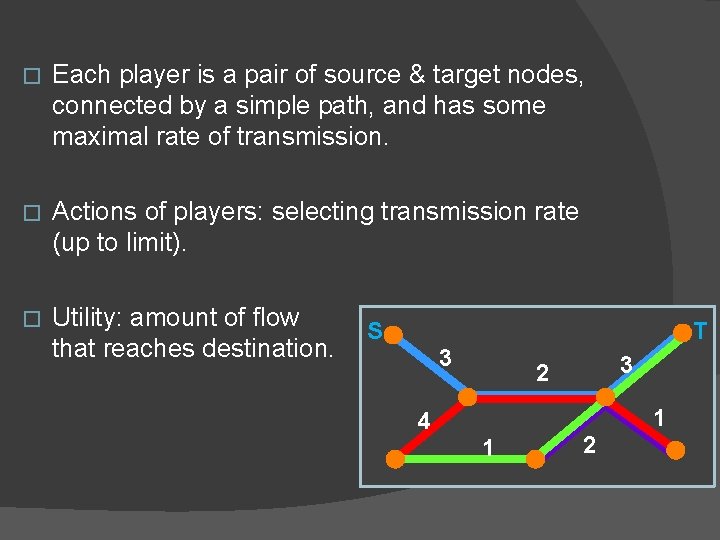
� Each player is a pair of source & target nodes, connected by a simple path, and has some maximal rate of transmission. � Actions of players: selecting transmission rate (up to limit). � Utility: amount of flow that reaches destination. S T 3 3 2 4 1 2 1

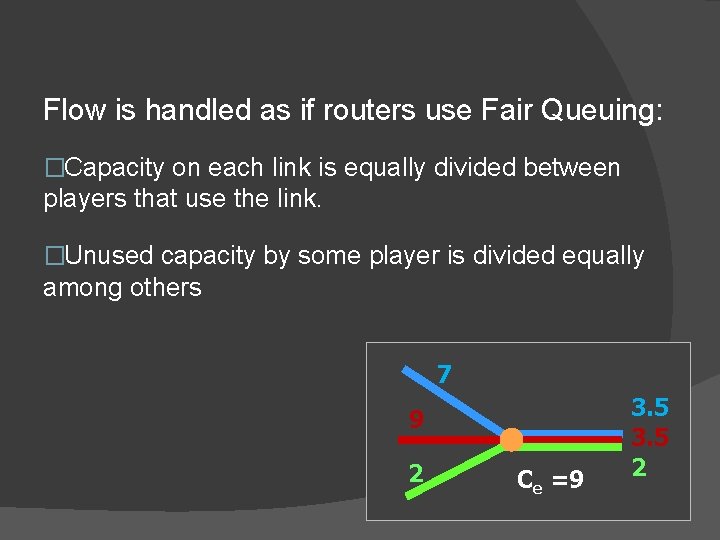
Flow is handled as if routers use Fair Queuing: �Capacity on each link is equally divided between players that use the link. �Unused capacity by some player is divided equally among others 7 9 2 Ce =9 3. 5 2

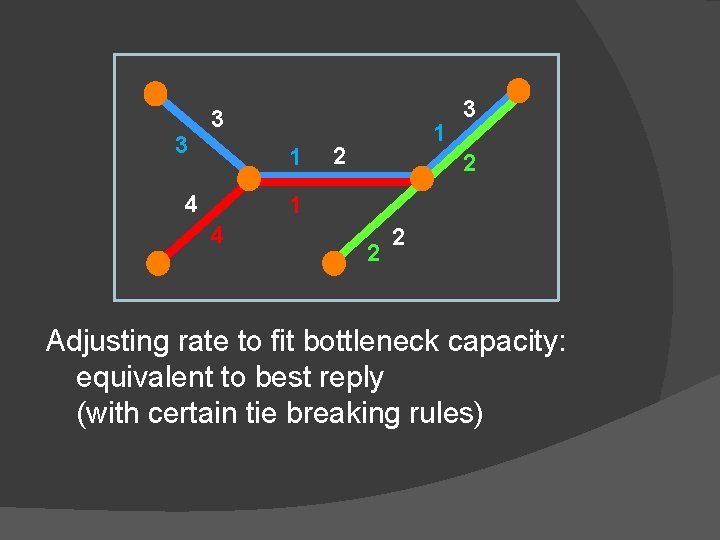
3 3 1 4 1 2 3 2 1 4 2 2 Adjusting rate to fit bottleneck capacity: equivalent to best reply (with certain tie breaking rules)

Results for Congestion Control Thm: The Congestion Control Game with routers that follow Fair-Queueing is NBRSolvable with a clear outcome.

� Eliminate all transmission rates below e* for them. � If they all transmit at least e*, none will manage to get more through. Eliminate all rates above e*. � Repeat with the residual graph and remaining players. Ce

Results for Congestion Control Thm: The Congestion Control Game with routers that follow Fair-Queueing is NBR-Solvable with a clear outcome. Corollaries: � Best-response is incentive compatible � Converges fast regardless of topology TCP’s actual behavior in this setting can be seen as probing for the best-response.

Other Games � Matching �Uncorrelated markets, interns and hospitals � Cost-sharing games � BGP – interdomain routing in the internet. 1 2 See the paper for more details and references! 3 4 d

Open Questions: � Explore other dynamics (e. g. , regret minimization) and other equilibria (e. g. , mixed Nash, correlated). � Find an exact characterization of games where repeated best-response is rational.

Thank You!