autmatos finitos com transies e p e q

autômatos finitos com transições e p e q o autômato vai do estado p para o estado q sem ler um símbolo de entrada.

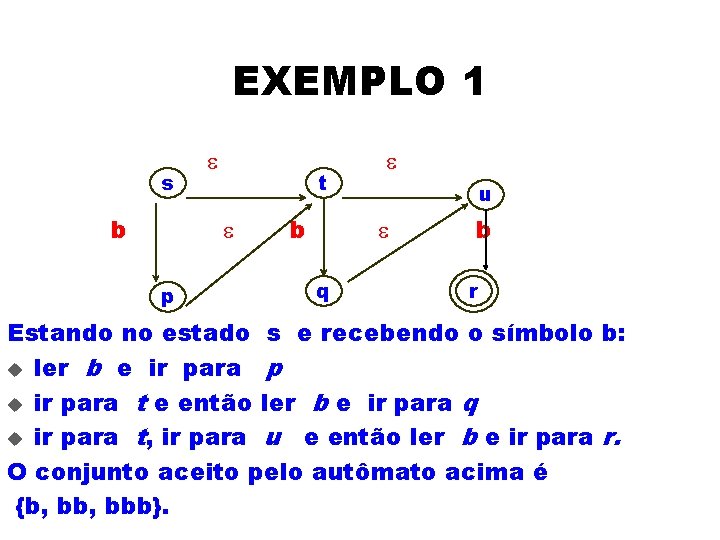
EXEMPLO 1 s b e t e p b e u e q b r Estando no estado s e recebendo o símbolo b: u ler b e ir para p u ir para t e então ler b e ir para q u ir para t, ir para u e então ler b e ir para r. O conjunto aceito pelo autômato acima é {b, bbb}.

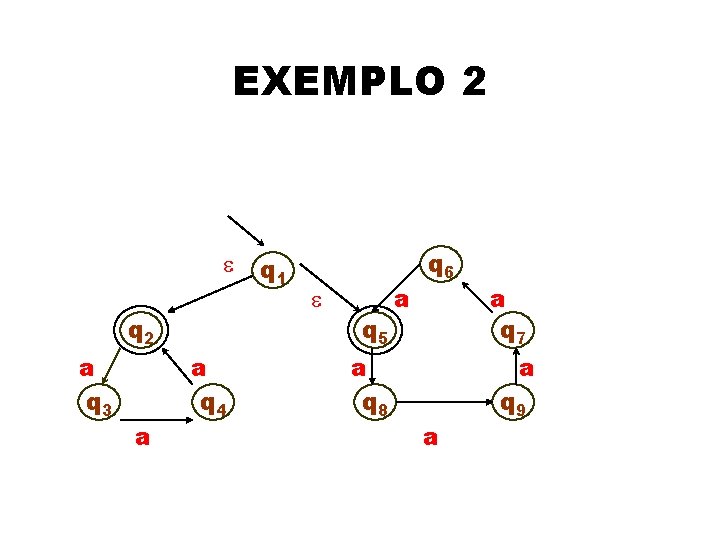
EXEMPLO 2 e q 2 a q 3 a a q 4 q 1 e q 5 a q 8 a q 6 a q 7 a a q 9

O conjunto aceito pelo autômato acima é { x Î {a*} | |x| é divisível por 3 ou 5}. A maior vantagem de transições é a conveniência. Autômato com transições tem o mesmo poder computacional que afds e afnds

Propriedades de Linguagens Regulares Concatenação de dois conjuntos A e B A • B = AB = { xy | x Î A e y Î B} EXEMPLO. {a, ab} • {b, ba} = {ab, aba, abba} Se A e B são conjuntos regulares, AB também é.

Prova Intuitiva Seja M o autômato para A e N para B. u Construir um novo autômato P cujo os estados são a união dos de M e N. u Todas as transições de M e N serão transições de P. u O estado inicial de M será o de P. u Os estados finais de N serão os de P. u Finalmente, ligue os estados finais de M ao estado inicial de N com uma transição e.

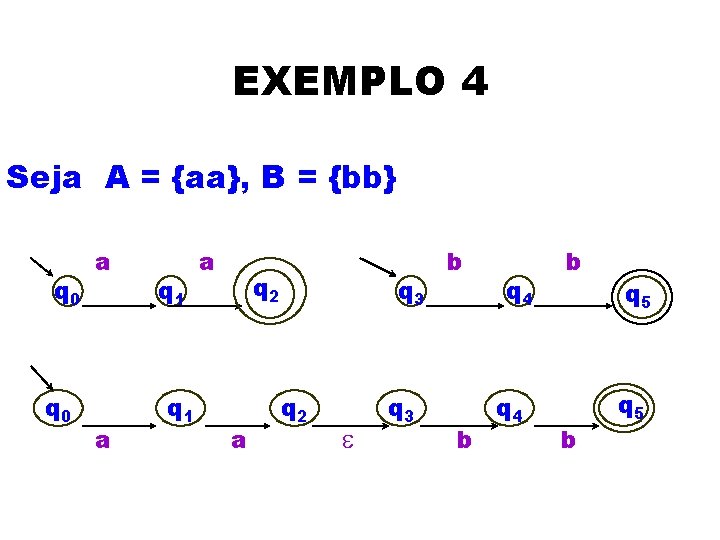
EXEMPLO 4 Seja A = {aa}, B = {bb} q 0 a a q 1 a q 2 a q 3 q 2 e q 3 b b q 4 b b q 5

Fecho de Kleene Se A é regular então A* também é. A* = { e} A A 2 A 3 … = { x 1 x 2…xn | n ³ 0 e xiÎA , 1 ói ó n}

Prova Intuitiva Seja M o autômato para A então P para A* é como segue: u Comece com todos os estados e transições de M. u Adicione um novo estado q e uma transição e de q para o estado inicial de M. Faça q o estado inicial de P. u Faça q o único estado final de P. transições e dos estados finais de M para o estado q. u Adicione

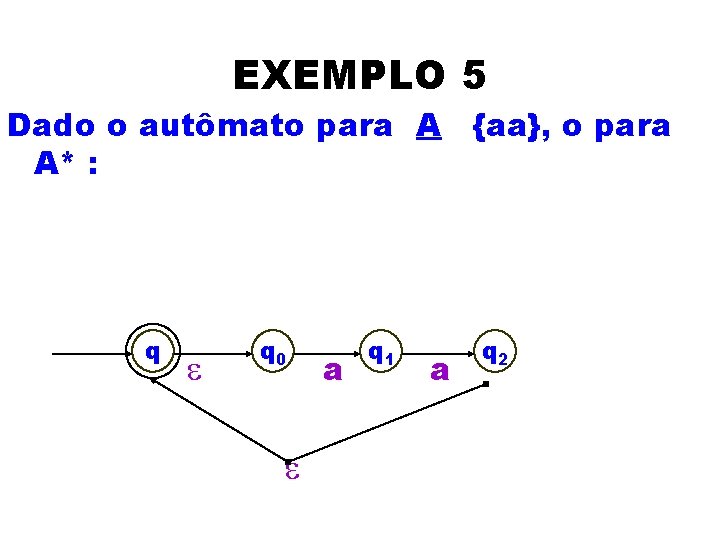
EXEMPLO 5 Dado o autômato para A {aa}, o para A* : q e q 0 e a q 1 a q 2

Casamento de Padrões e Expressões Regulares O que acontece quando digitamos ‘rm *’ no Unix? E ‘rm *. dvi’? Casamento de padrões é uma aplicação importante da teoria dos afds. Seja å um alfabeto finito. Um padrão é uma cadeia de símbolos de um certo formato representando um conjunto (possivelmente infinito) de cadeias sobre å*.

Casamento de Padrões: Básicos Compostos Notação: letras gregas , b , g , … Associado a definição de padrões, temos quais cadeias x Î å* casam com os padrões definidos. Notação: L( ) é o conjunto de cadeias em å* que casam um dado padrão . L(X) = {x Î å* | X casa com }

ua u Padrões Básicos para cada símbolo a Î å, L(a) = {a} casa com a palava vazia e, L( ) = { e } u f casa com nada, L(f) = f, o cjto. vazio u # casa com qualquer símbolo em å, L(#) = å u @ casa qualquer cadeia em å*, L(@)=å*.

Padrões compostos u São formados indutivamente usando os operadores: +, Ç, * , ~ , • u Suponha que definimos os conjuntos de cadeias L(a) e L(b) casando a e b respectivamente. Então dizemos: u x casa com a + b , se x casa ou com b L(a + b ) = L(a ) L(b)

u. X casa com a Ç b se X casa com ambos a e b L(a Ç b ) = L(a) Ç L(b) u X casa com ab se existem cadeias y e z tal que y casa com a, z casa com b e x = yz. L(ab) = L(a) • L(b) u X casa ~a se X não casa com a. L(~a) = ~ L(a ) = å* L(a) Esta definição depende de å.

u. X casa a* se x pode ser dividido na concatenação de várias (talvez nenhuma) cadeias finitas, x=x 1 x 2 x 3…xn, n ³ 0 tal que cada xi casa com a. L(a*) = {x 1 x 2…x n| n³ 0 e xiÎL(a), 1 £ i £ n} = L(a)0 L(a)1 L(a)2 …= L(a)* u Note que Padrões são cadeias de símbolos sobre o alfabeto: { a | a Î å } { , f , #, @, +, Ç, ~, *, (, )}

EXEMPLOS = L(@) = L(#*) u Conjuntos com um único símbolo: se x Î å* , então, x por se só é um padrão e casa somente com a cadeia x, i. e , {x} = L(x) u Conjuntos finitos: se x 1 , … , xm Î å* , então {x 1, x 2 , …, xm } = L(x 1 + x 2 + … + xm ) u å*

u cadeias contendo pelo menos 3 ocorrências de a: @a@a@a@ u cadeias contendo um a seguido mais tarde por um b, isto é cadeias da forma xaybz para algum x, y, z @a@b@ uå { a } # Ç (~a) u cadeias sem a ocorrência da letra a (# Ç (~a) ) *

Algumas Questões Importantes u Quão difícil é determinar se uma dada cadeia casa um determinado padrão? (Existem algoritmos muitos eficientes, veremos alguns deles. Esta é uma questão prática. u Todos os conjuntos são representados por algum padrão? (Não! Veremos, por exemplo, que o conjunto {an bn | n ³ 0} não é representado por nenhum padrão. )

u Quais operadores são redundantes? pois é equivalente a ~(#@) e a f* @ pois é equivalente a #* # se å = a 1 , a 2 , … , an então # é equivalente a a 1 + a 2 + … + an. Ç a Ç b é equivalente a ~(~a + ~ b)

u Todos os padrões são equivalentes a um padrão usando somente o padrão básico a para a Î å , f e os operadores ~, + , * e • . Padrões usando somente estes símbolos são chamados expressões regulares.

Evitando Parentesis + e. São associativas, i. e. L(a+(b+g)) = L((a+b)+g) L(a(bg)) = L((ab)g) , e podemos escrever a+b+g abg Precedência: * • Menor +

Equivalência de Padrões, Expressões Regulares e Autômatos Finitos Teorema: Seja A Í å*. As três afirmações abaixo são equivalentes: (i) A é regular; i. e. , A = L(M) para algum autômato finito M. (ii) A = L(a ) para algum padrão a (iii) A = L(a ) para alguma expressão regular a.

Prova: (iii) ® (ii) u A implicação (iii) ® (ii) é trivial, uma vez que toda expressão regular é um padrão por definição.

(ii) ® (i) O coração desta prova envolve mostrar que outros conjuntos básicos (correspondendo aos padrões básicos) são regulares, e que conjuntos são fechados sobre operações de fechamento correspondendo aos operadores usados para construir padrões.

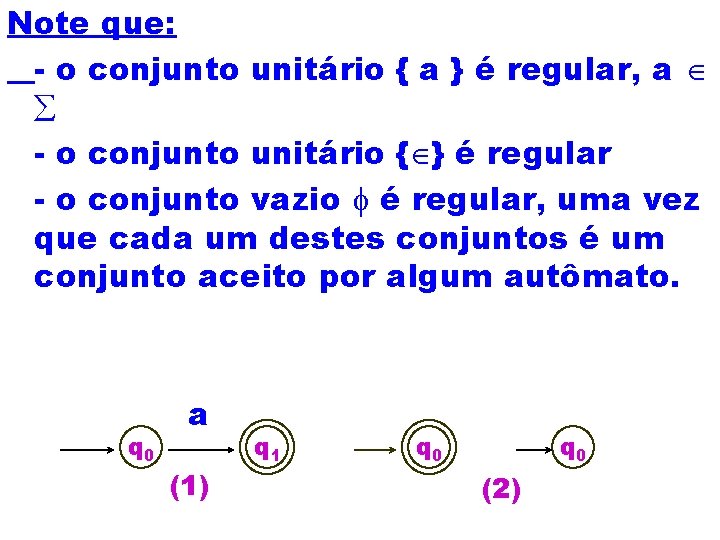
Note que: - o conjunto unitário { a } é regular, a Î å - o conjunto unitário {Î} é regular - o conjunto vazio f é regular, uma vez que cada um destes conjuntos é um conjunto aceito por algum autômato. q 0 a (1) q 1 q 0 (2)

Mostramos previamente que os conjuntos regulares são fechados sobre o conjunto de operações , Ç, ~ , *, e, ·, i. e. , se A e B são conjuntos regulares então A B, A Ç B, ~A = å* A, AB e A* são regulares. Seja a um dado padrão. Queremos mostrar que L(a) é um conjunto regular. Procedemos por indução na estrutura de a.

O padrão é de uma das seguintes formas: (i) a, para algum a Î å (ii) Î (iii) f (iv) # (v) @ (vi) b+g (vii) bÇg (viii) bg (ix) ~b (x) b*

São cinco casos base (i) - (v) correspondendo aos padrões atômicos e cinco casos de indução correspon-dendo aos padrões compostos. u. Para (i) - (iii) temos L(a) = {a} para a Î å, L(Î) = {Î} e L(f) = f estes são conjuntos regulares. u. Para (iv) e (v), argumentamos antes que os operadores # e @ são dundantes logo podemos desconsiderar estes casos.

u Para (vi), lembre que L(b+g) = L(b) L(g) pela definição do operador +. Pela hipótese da indução, L(b) e L(g) são regulares. Como conjuntos regulares são fechados sobre a união, L(b+g) = L(b) L(g) é regular. u Para os casos (vii) - (x) use argumentos similares aos usados em (vii).

convertendo autômatos em expressões regulares (I) ® (iii) Dado um subconjunto de estados T de um AFND M e estados u e v, construamos a expressão regular: Tuv representando o conjunto de todas as cadeias x tal que existe um caminho de u para v em M rotulado x (isto é , d*(u, x) = v) e todos os estados no caminho, com a possível exceção de u e v estarem em T.

As expressões são construídas por indução no tamanho de T. Base T = f Seja a 1, … , ak todos os símbolos em å tal que d (u, ai) = v. afuv = a 1 + … + ak se u ¹ v a 1 + … + ak + Î se u = v

Indução T¹f Escolha um elemento qualquer q Î T a. Tuv = auv. T-{q} + auq. T-{q} (aqq. T-{q} )* aqv. T-{q}

Note qualquer caminho de u para v com todos os estados intermediários em T ou : (i) nunca visita q : auv. T-{q} ou (ii) visita q uma primeira vez: auq. T-{q} Seguido por um número finito (≥ zero) de laços de q para q sem visitar q no meio tempo e ficando em q : (aqq. T-{q} )* Seguido por um caminho de q para v deixando q pela última vez aqv. T-{q}

A expressão: a. Qsf 1 + a. Qsf 2 + … + a. Qsfk representa o conjunto de cadeias aceitas por M, onde Q é o conjto de todos os estados de M, s é o estado inicial e { f 1 , … , fk } é o conjunto de estados finais.

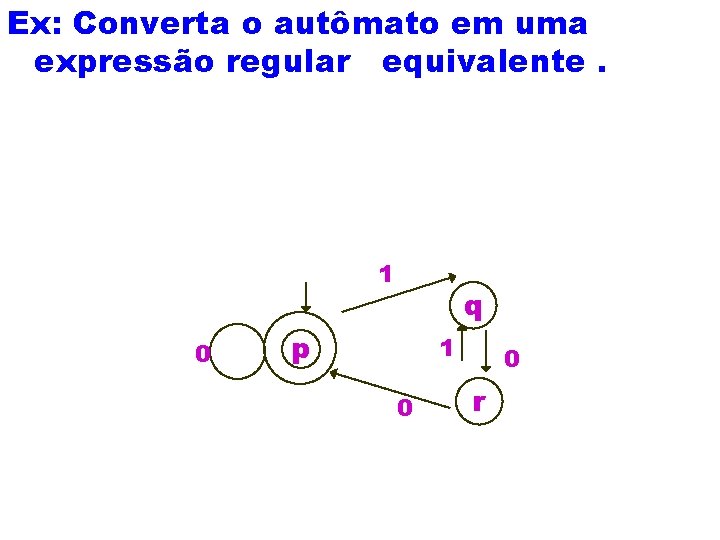
Ex: Converta o autômato em uma expressão regular equivalente. 1 0 q p 1 0 0 r

T={p, q, r} pp{p, q, r} Remova q {p, q, r} = pp pp{p, r} T- {q} pp{p, r} + pq {p, r}( qq{p, r})* qp{p, r} = 0* pq{p, r} = 0*1 qq{p, r} = + 01 + 000*1 qp{p, r} = 000* pp{p, q, r} = 0* + 0*1 ( + 01 + 000*1 )*000*