Mtodo dos Elementos Finitos Teoria Eletromagntica IIC Prof

Método dos Elementos Finitos Teoria Eletromagnética IIC Prof. Antonio Lopes de Souza, Ph. D. (Modelo estrutural em elementos finitos do Cubo d’Água de Pequim)

Soluções Para Problemas do Eletromagnetismo Solução Analítica: solução na forma de uma equação algébrica explícita, na qual todos os valores dos parâmetros do problema podem ser substituídos. Ex. : campo elétrico da carga pontual Vantagens das soluções analíticas: são exatas e tornam mais fácil observar o comportamento da solução em função da variação dos parâmetros do problema. Figura 2 - Linhas de força do campo elétrico de um sistema de duas cargas pontuais Desvantagem: somente são possíveis para problemas com configurações simples e elevado grau de simetria.

Soluções Para Problemas do Eletromagnetismo Solução não Analítica: é usada quando a complexidade do problema torna difícil a obtenção de uma solução analítica por métodos matemáticos tradicionais. Os procedimentos não-analíticos incluem v. Métodos gráficos v. Métodos experimentais v. Métodos numéricos Os métodos gráficos e experimentais são aplicados a um número reduzido de problemas e têm utilidade limitada. Os métodos numéricos mais usados são: v. Método das Diferenças Finitas (FDM - Finite Diference Method) v. Método dos Momentos (MOM - Method of Moments) v. Método dos Elementos Finitos (FEM – Finite Diference Method)

Soluções Para Problemas do Eletromagnetismo Solução Não-analítica: exemplo Figura 3 - Visualização da deformação de um carro em um choque assimétrico usando o método dos elementos finitos (imagem: Wikimedia Commons)

Método dos Elementos Finitos O Método dos Elementos Finitos (FEM – Finite Element Method) é uma técnica numérica usada para encontrar a solução de Equações Diferenciais Parciais (PDE). Ele surgiu na década de 40 do século passado e era usado para resolver problemas estruturais nas engenharias civil e aeronáutica. Os primeiros trabalhos sobre o método foram publicados por Alexander Hrennikoff (1) (1941) e Richard Courant (2) (1942). O uso do método para a soluções de problemas de eletromagnetismo data de 1968 (3). Figura 5: Solução bidimensional de um problema de magetostática mostrando a direção (as linhas) e a intensidade (cores) da densidade de fluxo magnético. (imagem: Wikimedia Commons). Esquerda: Malha do problema Direita: Solução gráfica do problema (1) A. Hrennikoff; “Solution of Problems of Elasticity by the Frame-Work Method” (1941); ASME J. Appl. Mech. 8; A 619–A 715. (2) Courant, R. L; “Variational Methods for the Solution of Problems of Equilibrium and Vibration”; Bulletin of the American Mathematical Society 49: 1 -23 (1943). (3) P. P. silvester e R. L. Ferrari; Finite Elements for Electrical Enginiers, Cambridge, England, Cambridge University Press, (1983).

Método dos Elementos Finitos Etapas na modelagem de um problema através do Método dos Elementos Finitos: v Descrição geométrica da região; v. Geração de uma malha de elementos interconectados por nós; v. Definição das equações diferenciais parciais e respectivas de contorno do problema; v. Solução numérica do sistema algébrico resultante; v. Pós-processamento de resultados e visualização condições

Método dos Elementos Finitos Sequência na apresentação do método: 1. Discretização do domínio em um número finito sub-regiões ou elementos. 2. Obtenção das equações que regem um elemento típico. 3. Conexão de todos os elementos no domínio. 4. Resolução do sistema de equações obtido.

Método dos Elementos Finitos 1 - Discretização A representação do domínio: o domínio é dividido em regiões (elementos) que não se sobrepõem. Buscamos uma aproximação para o potencial Ve dentro de um elemento. Inter-relacionamos as distribuições de potencial em vários elementos de tal modo que ela seja contínua através dos contornos entre os elementos relacionados. A solução aproximada do potencial para o domínio em estudo é do tipo: Onde N é o número de elementos triangulares nos quais o domínio foi dividido Figura 6 – elemento triangular com a indicação dos nós e tensões de nós. A orientação dos nós segue o sentido anti-horário.

Método dos Elementos Finitos 1 - Discretização Representação do potencial no interior do elemento: quando o elemento tem a forma triangular a forma mais comumente usada para representar o potencial Ve no seu interior é a aproximação polinomial Quando o elemento for quadrangular a aproximação para representar Ve é dada por: De um modo geral usamos elementos triangulares para problemas bidimensionais porque esses permitem representar fronteiras irregulares com maior precisão. Supomos que o potencial varia linearmente dentro do elemento. Isso implica em considerar o campo elétrico é uniforme dentro de um mesmo elemento. Como os potenciais respeitam a equação de Laplace a distribuição de energia do campo elétrico é mínima na região.

Método dos Elementos Finitos 2 - Equações que regem os elementos O elemento usado tem a forma triangular abaixo mostrada: O potencial no seu interior é representado por: Aplicando a equação aos três vértices do elemento temos:

Método dos Elementos Finitos 2 - Equações que regem os elementos Representando o sistema de equações anterior na forma matricial temos: Onde a matriz É denominada “matriz dos coeficientes”

Método dos Elementos Finitos 2 - Equações que regem os elementos Os coeficientes a, b, c podem ser calculados a partir da equação anterior como: E usando a regra de CRAMER Onde D é o determinante da matriz dos coeficientes dado por

Método dos Elementos Finitos 2 - Equações que regem os elementos É possível mostrar que a área A do triangulo que representa o elemento é dada por: (Os nós devem ser numerados no sentido anti-horário para evitar que a área do elemento, acima calculada em função das coordenadas dos vértices, produza um valor negativo) Ou seja:

Método dos Elementos Finitos 2 - Equações que regem os elementos Substituindo o valor D=2 A em a, b, e c e resolvendo os determinantes temos:

Método dos Elementos Finitos 2 - Equações que regem os elementos As equações anteriores podem ainda ser colocadas na forma matricial como: Lembrando a forma matricial da equação que descreve as distribuições de potencial,

Método dos Elementos Finitos 2 - Equações que regem os elementos Substituindo as expressões matriciais para a, b e c na equação matricial que descreve as distribuições de potenciais no elemento temos: Expandindo a equação acima temos: Ou seja:

Método dos Elementos Finitos 2 - Equações que regem os elementos e a 1, a 2 e a 3 são funções lineares de interpolação que permitem a obtenção dos potenciais Ve(x, y) dentro do elemento finito em termos dos potenciais nos nós do mesmo elemento. Elas são denominadas “Funções de Forma dos Elementos”. Desse modo a função nos dá o potencial em qualquer ponto (x, y) dentro do elemento finito, desde que os potenciais nos vértices sejam conhecidos.

Método dos Elementos Finitos 2 - Equações que regem os elementos As funções de propriedades: forma do elemento satisfazem as seguintes Cada uma das três funções de forma se anula em todos os vértices com exceção de um no qual assume o valor unitário. Cálculo da Energia Armazenada no Elemento Quando a quantidade analisada é o potencial eletrostático a energia do campo elétrico é o funcional a ser utilizado porque o potencial eletrostático minimiza esta energia. A energia do campo elétrico por unidade de comprimento normal às duas dimensões (ou seja, na direção z) pode ser obtida por:

Método dos Elementos Finitos 2 - Equações que regem os elementos A função de energia pode ser expandida como abaixo: Onde O produto escalar produzirá termos cruzados (ver o detalhamento no texto disponível na pasta do curso – pasta 187 ) e isso permitirá colocar a função de energia na forma abaixo: Denominando (O termo Cij(e) pode ser considerado como o acoplamento entre os nós i e j)

Método dos Elementos Finitos 2 - Equações que regem os elementos A equação da energia armazenada no campo elétrico onde é o acoplamento entre os nós i e j pode ser escrita na forma matricial como: onde A matriz C(e) é denominada “Matriz dos Coeficientes do Elemento”

Método dos Elementos Finitos 2 - Equações que regem os elementos Cálculo dos Termos da Matriz dos Coeficientes do Elemento Cálculo de C 12(e) Precisamos calcular E resolvendo a integral temos que

Método dos Elementos Finitos 2 - Equações que regem os elementos Logo: Os outros coeficientes podem ser calculados de modo semelhante Usando a notação: Podemos escrever

Método dos Elementos Finitos 2 - Equações que regem os elementos Em resumo: para a obtenção da função potencial no elemento é necessário conhecer as funções de forma a 1, a 2 e a 3 cujo cálculo depende do valor das coordenadas dos vértices do elemento triangular. O cálculo da energia do elemento pode ser feito Onde Como todos os elementos são escritos em função das diferenças entre as coordenadas podemos definir novas variáveis P e Q como abaixo As novas variáveis satisfazem as seguintes propriedades:

Método dos Elementos Finitos 3 - Conexão de todos os elementos Após a análise de um elemento típico o próximo passo é a conexão de todos os elementos. A energia associada à conexão de todos os elementos da malha é o somatório das energia armazenadas nos elementos: onde Nas equações acima “N” é o número de elementos e “n” é o número de nós. A matriz [C ] é denominada Matriz de Rigidez Global e representa a conexão das matrizes dos coeficientes dos elementos individuais. Não confundir [C] com [C(e)]. Os coeficientes Cij são obtidos observando-se o fato de que os potenciais devem ser contínuos através dos contornos dos elementos

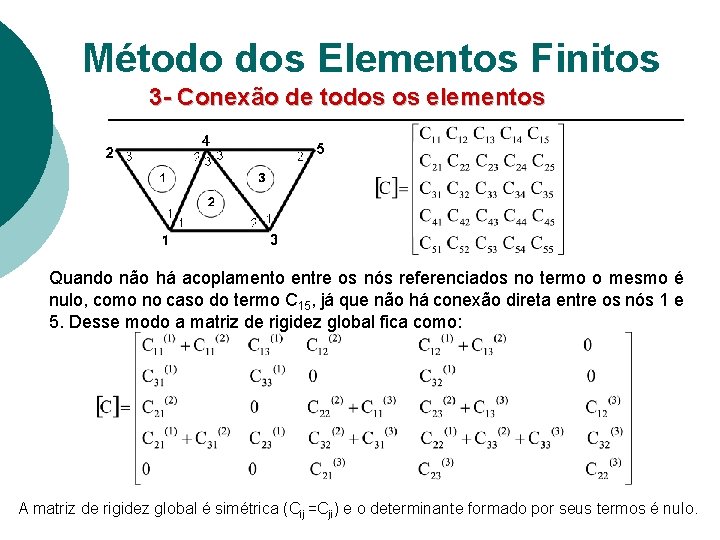
Método dos Elementos Finitos 3 - Conexão de todos os elementos Considere a malha de três elementos abaixo: Numeração global: 1, 2, 3, 4, 5 (nós da malha, qualquer ordem) Numeração local: 1, 2, 3 (vértices do elemento, sempre no sentido antihorário para evitar que a área fique negativa) Para o elemento 3 a numeração global 3, 4, 5 corresponde à numeração local 1, 2, 3 respectivamente.

Método dos Elementos Finitos 3 - Conexão de todos os elementos Como a malha tem cinco nós globais a matriz de rigidez global é do tipo 5 x 5. Note que a matriz de rigidez global é a superposição de todas a matrizes dos elementos. Como muitos potenciais são iguais, vários termos da matriz se superpõem de modo que a mesma fica reduzida a uma matriz de estrutura nxn, onde n é o número de nós globais. Para obter o termo C 11 notamos que o nó global 1 pertence aos elementos 1 e 2. Notamos, também que os nós locais que fazem parte do nó global 1 são os nós locais 1 de ambos os elementos, logo: Já o coeficiente C 14 é calculado lembrando que a fronteira global 1 -4 contem as fronteiras 1 -2 do elemento 1 e 1 -3 do elemento 2, então:

Método dos Elementos Finitos 3 - Conexão de todos os elementos Quando não há acoplamento entre os nós referenciados no termo o mesmo é nulo, como no caso do termo C 15, já que não há conexão direta entre os nós 1 e 5. Desse modo a matriz de rigidez global fica como: A matriz de rigidez global é simétrica (Cij =Cji) e o determinante formado por seus termos é nulo.

Método dos Elementos Finitos 4 - Resolução das equações resultantes Do cálculo variacional temos que a equação de Laplace é satisfeita no domínio quando a energia total no mesmo é mínima. Portanto é necessário que as derivadas de W em relação ao potencial de cada nó sejam zero. Isso permite estabelecer um sistema de equações que nos levará ao cálculo dos potenciais dos nós globais V 1, V 2, V 3. . . Vn, onde n é o número de nós globais.

Método dos Elementos Finitos 4 - Resolução das equações resultantes Temos que a energia elétrica armazenada em todo o domínio é dada por: Onde a matriz dos potenciais dos nós globais é dada por Desmembrando a equação da energia temos, para o exemplo tomado com três elementos e cinco nós globais:

Método dos Elementos Finitos 4 - Resolução das equações resultantes O produto das matrizes [C] e [V] gera uma matriz coluna como abaixo mostrada:

Método dos Elementos Finitos 4 - Resolução das equações resultantes mas como C 12=C 21 temos como Ou no geral: Dese modo obtemos um conjunto de equações que pode ser resolvido para obter V 1, V 2, V 3, V 4, V 5

Método dos Elementos Finitos 4 - Resolução das equações resultantes FIM