Informtica Terica Cincia da Computao Autmatos Finitos Operaes

Informática Teórica Ciência da Computação

Autômatos Finitos Operações Regulares n n n Em aritmética, os objetos básicos são números e as ferramentas são operações para manipulá-los, tais como + e . Na teoria da computação os objetos são linguagens e as ferramentas incluem operações especificamente projetadas para manipulá-las. Definimos três operações sobre linguagens, chamadas operações regulares, e as usamos para estudar propriedades de linguagens regulares.

Definição Operações Regulares n Sejam A e B linguagens. Definimos as operações regulares união, concatenação, e estrela da seguinte forma. União: A B = {x | x A ou x B}. n Concatenação: A B = {xy | x A e y B}. n Estrela: A* = {x 1 x 2. . . xk | k≥ 0 e cada xi A}. n

Operações regulares Exemplo n n Suponha que o alfabeto seja o alfabeto padrão de 26 letras {a, b, . . . , z}. Se A = {legal, feliz} e B = {garoto; garota}, então A B = {legal, feliz, garoto, garota}, A B = {legalgaroto, legalgarota, felizgaroto, felizgarota}, e A* = { , legal, feliz, legal, legalfeliz, felizlegal, feliz, legallegal; legalfeliz, legalfelizlegal, legalfeliz, . . . }.

Definição Operações Regulares n Como linguagens são conjuntos, então todas as operações sobre conjuntos que estudamos em matemática discreta também são válidas para linguagens. n A novidade aqui foi a operação estrela e a concatenação de conjuntos n Vamos estudar a operação estrela com mais detalhes.

Definição Potências de um conjunto n As potências An de um conjunto são definidas indutivamente como a seguir: A 0 = { } n An+1 = AAn n Em outras palavras, o conjunto An é formado pela concatenção de n cópias de A. n Temos também a seguinte propriedade Am+n= Am. An n

Definição Potências de um conjunto. Exemplos. n {ab, cd}0 = § { } n {ab, cd}1 = § {ab, cd} n {ab, cd}2 = § {abcd, abab, cdcd} n {ab, cd}3 = § {ababab, ababcd, abcdab, cdabab, cdcdab, c dcdcd, cdabcd, abcdcd}

Definição Operação Estrela n A* é a união de todas as potências finitas de A: n A* = An , n 0 n A* = A 0 A 1 A 2 A 3 … n Definimos também A+ = AAn = An , n>0

Propriedades Operação Concatenação n { }A = A{ } = A n A = A = n Associatividade: – (AB)C = A(BC)

Propriedades Operação Concatenação n Distributiva em relação à união: – A(B C) = AB AC – (A B)C = AC BC n Você acha que a concatenação é distributiva em relação à interseção? Tente construir um exemplo. n Seja A={a, ab}, B={b} e C={ } n Compute A(B C) e AB AC

Propriedades Operação Estrela n A*A* = A* n A* = { } AA* = { } A*A n * = { }

Operações Regulares Teorema: A classe de linguagens regulares é fechada sob a operação de união. n Em outras palavras, se A 1 e A 2 são linguagens regulares, o mesmo acontece com A 1 A 2. n Idéia da Prova: Se A 1 e A 2 são linguagens regulares, então existem AFs M 1 e M 2 que as reconhecem, respectivamente. n Vamos fazer uma prova construtiva, ou seja, vamos construir um AF M, que reconheça A 1 A 2, a partir de M 1 e M 2. n

Operações Regulares n n n Como vamos construir um AF M, que reconheça A 1 A 2, a partir de M 1 e M 2? Simulando M 1 e M 2 simultaneamente. Para controlar ambas as simulações é preciso guardar o estado em que cada máquina estaria se ela tivesse lido até um ponto na entrada. Consequentemente, você precisa guardar um par de estados. Quantos pares de estados existem?

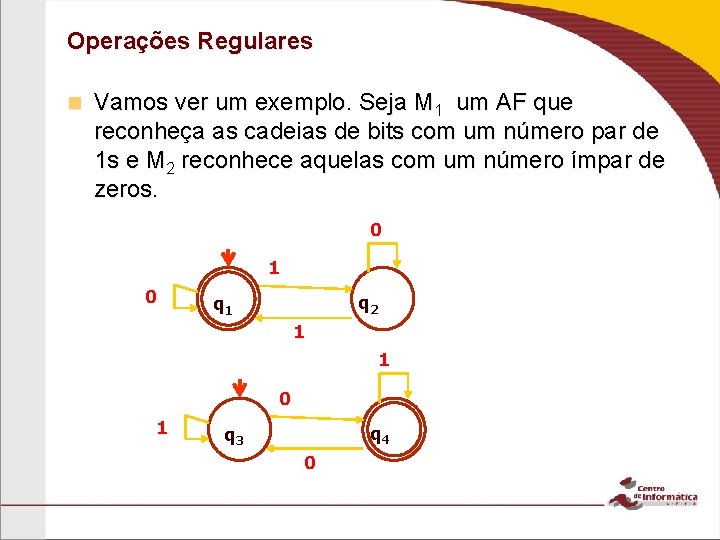
Operações Regulares n Vamos ver um exemplo. Seja M 1 um AF que reconheça as cadeias de bits com um número par de 1 s e M 2 reconhece aquelas com um número ímpar de zeros. 0 1 0 q 2 q 1 1 1 0 1 q 4 q 3 0

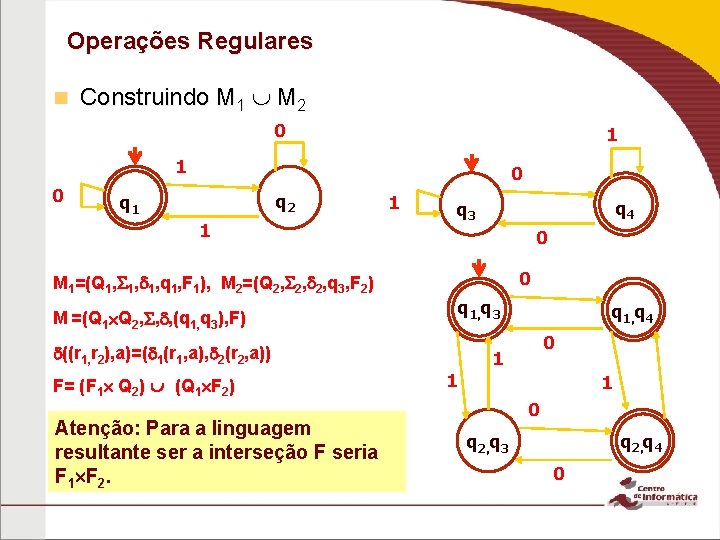
Operações Regulares n Construindo M 1 M 2 0 1 1 0 0 q 2 q 1 1 1 q 4 q 3 0 0 M 1=(Q 1, 1, 1, q 1, F 1), M 2=(Q 2, 2, 2, q 3, F 2) q 1, q 3 M =(Q 1 Q 2, , , (q 1, q 3), F) ((r 1, r 2), a)=( 1(r 1, a), 2(r 2, a)) F= (F 1 Q 2) (Q 1 F 2) Atenção: Para a linguagem resultante ser a interseção F seria F 1 F 2. q 1, q 4 0 1 1 1 0 q 2, q 4 q 2, q 3 0

Operações Regulares n n n Teorema: A classe de linguagens regulares é fechada sob a operação de concatenação. Em outras palavras, se A 1 e A 2 são linguagens regulares, o mesmo acontece com A 1 A 2. De modo análogo à prova do teorema anterior, vamos construir um autômato M para reconhecer A 1 A 2 a partir de M 1 e M 2. M aceita sua entrada se ela puder ser quebrada em duas partes, onde M 1 aceita a primeira parte e M 2 aceita a segunda parte. O problema é que M não sabe onde quebrar sua entrada. Para resolver esse problema introduzimos uma nova técnica chamada não-determinismo.