Informtica Terica Cincia da Computao Autmatos Finitos um

Informática Teórica Ciência da Computação

Autômatos Finitos É um dos modelos computacionais que estudaremos. n Porém com uma quantidade extremamente limitada de memória. n O que um computador pode fazer com uma memória tão pequena? n Na verdade, interagimos com tais computadores o tempo todo, pois eles residem no coração de vários dispositivos eletromecânicos. n

Autômatos Finitos O controlador para uma porta automática é um exemplo de tal dispositivo. n As lavadoras de louça/roupa, termômetros eletrônicos, relógios digitais, calculadoras e máquinas de venda automática. . n Os autômatos também são chamados de máquinas de estados finitos. n

Autômatos Finitos: exemplo Controlador para uma porta automática de entrada Sinal de entrada Estado Nenhum Frente Atrás Ambos Fechado Aberto Fechado Aberto Esse controlador é um computador com apenas 1 bit de memória, capaz de registrar em quais dois estados o controlador está.

Autômatos Finitos n Ao começar a descrever a teoria matemática de autômatos finitos, fazemos isso no nível abstrato, sem refer� ência a qualquer aplicação específica. n A seguir vamos ver alguns exemplos usando um diagrama de estados e identificar os conceitos de: estado inicial, estado de aceitação ou final, transição.

Autômatos Finitos n Uma máquina M 1 que recebe cadeias de bits como entrada e aceita somente aquelas que começam com um ou mais zeros seguidos de um ou mais 1’s apenas.

Autômatos Finitos O autômato recebe os símbolos da cadeia de entrada um por um da esquerda para a direita. n Após ler cada símbolo, M 1 move de um estado para outro ao longo da transição que tem aquele símbolo como seu rótulo. n Quando ele lê o último símbolo, M 1 produz sua saída. n A saída é aceite se M 1 está agora no estado de aceitação e rejeite se ele não está. n

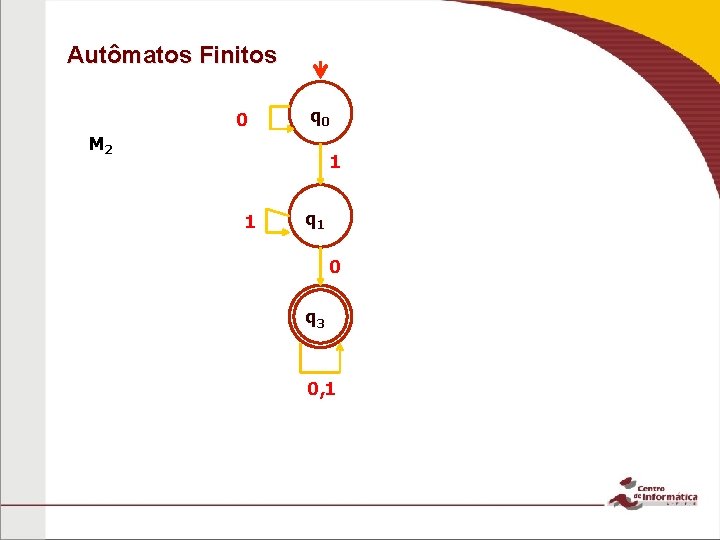
Autômatos Finitos n Um AF M 2 que recebe cadeias de bits e aceita aquelas que possuem 10 como subcadeia

Autômatos Finitos 0 q 0 M 2 1 1 q 1 0 q 3 0, 1

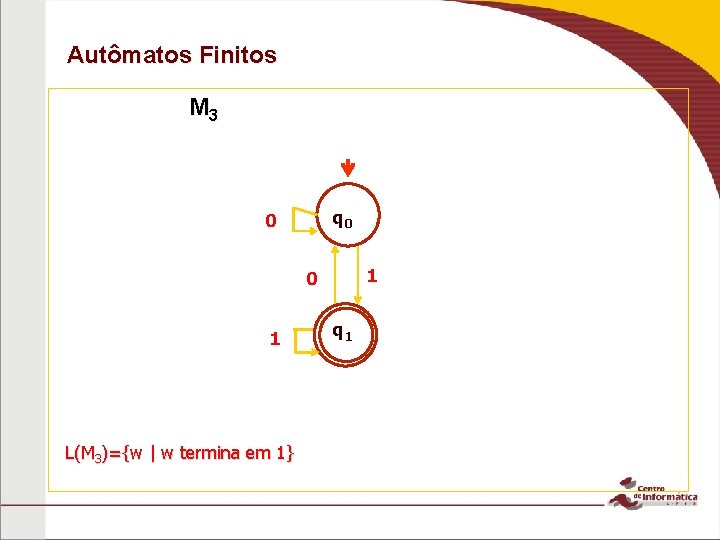
Autômatos Finitos M 3 q 0 0 1 L(M 3)={w | w termina em 1} q 1

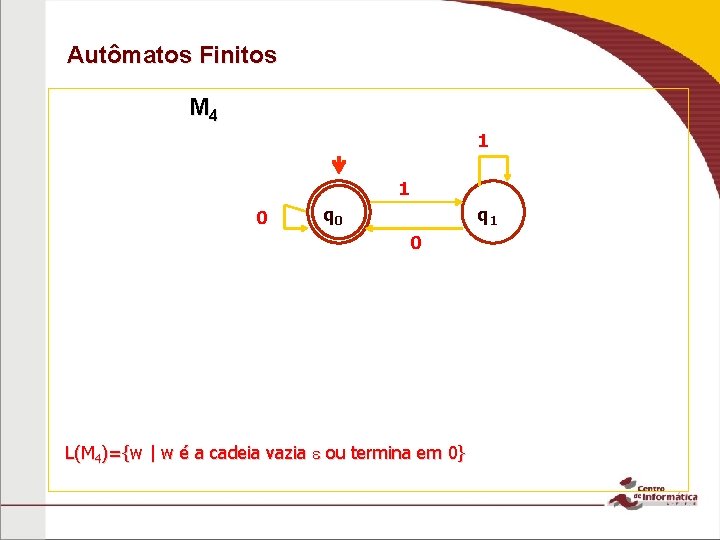
Autômatos Finitos M 4 1 1 0 q 1 0 L(M 4)={w | w é a cadeia vazia ou termina em 0}

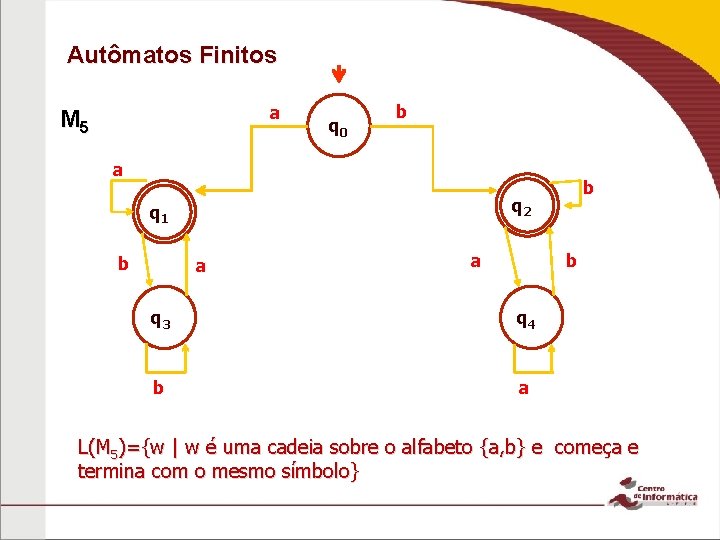
Autômatos Finitos a M 5 q 0 b a q 2 q 1 b b a a b q 3 q 4 b a L(M 5)={w | w é uma cadeia sobre o alfabeto {a, b} e começa e termina com o mesmo símbolo}

Autômatos Finitos a q 0 b q 1 a b q 2 a q 3 b a, b Os estados q 1 e q 2 servem para “memorizar’’ o símbolo anterior. Esse AF aceita as cadeias sobre o alfabeto {a, b} que possuem aa ou bb como subcadeias.

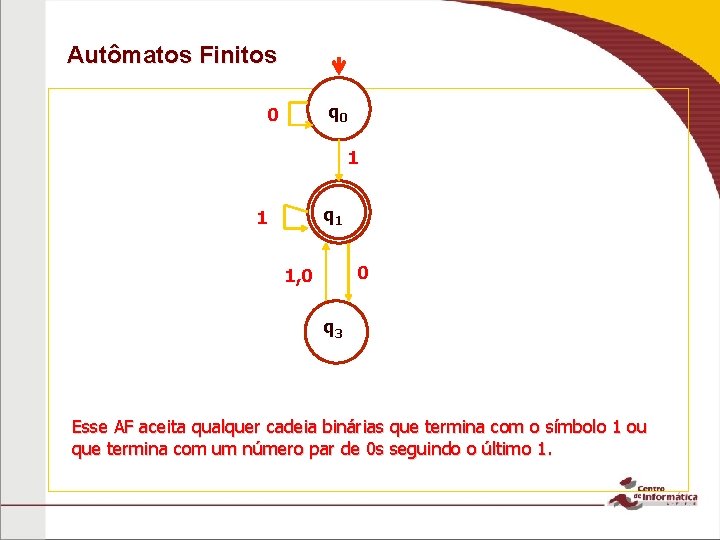
Autômatos Finitos q 0 0 1 q 1 1 0 1, 0 q 3 Esse AF aceita qualquer cadeia binárias que termina com o símbolo 1 ou que termina com um número par de 0 s seguindo o último 1.

Autômatos Finitos Descrição Formal n n n n A definição formal define precisamente as partes de um autômato finito: conjunto de estados, alfabeto de entrada, regras para movimentação, estado inicial e estados de aceitação�. Em linguagem matemática, uma lista de cinco elementos é frequentemente chamada 5 -upla.

Definição Formal n Um autômato finito é uma 5 -upla (Q, , , q 0, F), onde 1. Q é um conjunto finito denominado os estados, 2. é um conjunto finito denominado alfabeto, 3. : Q Q é a função de transição, 4. q 0 Q é o estado inicial, e 5. F Q é o conjunto de estados de aceitação (ou finais).

Autômatos Finitos Definição formal n Se A é o conjunto de todas as cadeias que a máquina M aceita, dizemos que A é a linguagem da máquina M e escrevemos L(M) = A. n Dizemos que M reconhece A ou que M aceita as cadeias de A. n Agora, vamos definir formalmente os AFs dos exemplos anteriores.

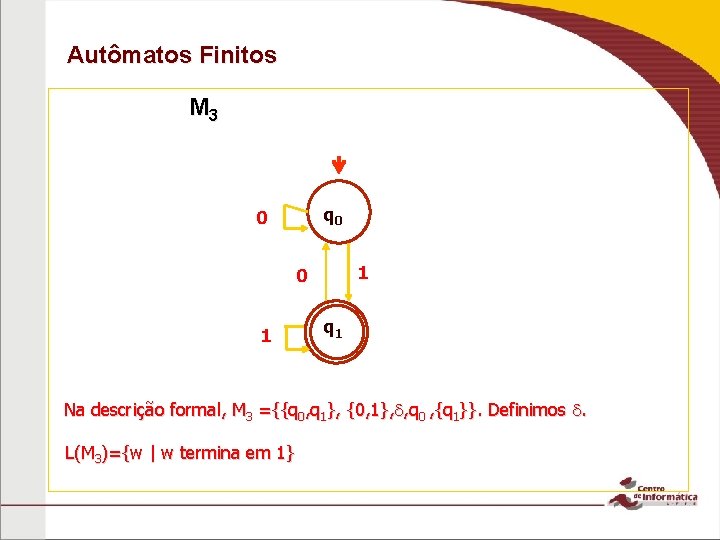
Autômatos Finitos M 3 q 0 0 1 q 1 Na descrição formal, M 3 ={{q 0, q 1}, {0, 1}, , q 0 , {q 1}}. Definimos . L(M 3)={w | w termina em 1}

Autômatos Finitos M 4 1 1 0 q 1 0 Note que, em razão do estado inicial também ser um estado de aceitação, M 4 aceita a cadeia vazia . L(M 4)={w | w é a cadeia vazia ou termina em 0}

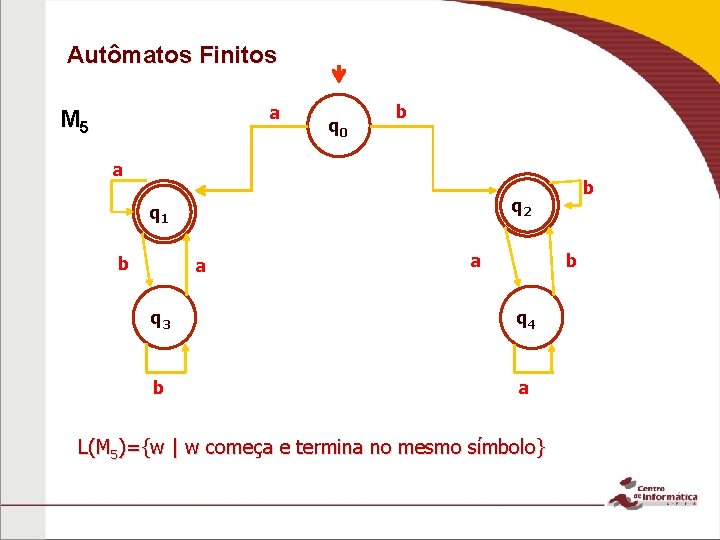
Autômatos Finitos a M 5 q 0 b a q 2 q 1 b b a a b q 3 q 4 b a L(M 5)={w | w começa e termina no mesmo símbolo}

Definição Formal de computação n n 1. 2. 3. Seja M= (Q, , , q 0, F) um autômato finito e suponha que w = w 1 w 2. . . wn seja uma cadeia onde cada wi é um membro do alfabeto. M aceita w se uma sequência de estados r 0, r 1. . . rn em Q existe com três condições: r 0 = q 0 , (ri, wi+1) = ri+1, para i = 0, . . . , n-1; e rn F. Dizemos que M reconhece a linguagem A se A = {w | M aceita w}.

Definição Linguagem Regular n Uma linguagem é chamada de uma linguagem regular se algum autômato finito a reconhece.

Projetando Autômatos Finitos Suponha que lhe é dada alguma linguagem e você deseja projetar um AF que a reconheça. n Faça de conta que você é o autômato. Você recebe uma cadeia de entrada e tem que determinar se ela é um membro da linguagem que o AF é suposto reconhecer. n Você vai vendo os símbolos na cadeia um por um. Depois de cada símbolo você tem que decidir se a cadeia vista até então está na linguagem. A razão é que você, como a máquina, não sabe quando o final da cadeia está vindo, portanto você tem que estar sempre pronto com a resposta. n

Projetando Autômatos Finitos: Exemplo Suponha que alfabeto seja {0, 1} e que a linguagem consista de todas as cadeias com um número ímpar de 1 s. n Faça de conta que você é o autômato M, que reconhece essa linguagem. Você recebe uma cadeia de entrada de 0 s e 1 s. n Você precisa lembrar a cadeia inteira vista até então para determinar se o número de 1 s é ímpar? n

Projetando Autômatos Finitos: Exemplo n n 1. 2. Basta lembrar se o número de 1 s visto até então é par ou ímpar e manter essa informação à medida que lê novos símbolos. Você representa essa informação como uma lista finita de possibilidades: par até agora, e ímpar até agora.

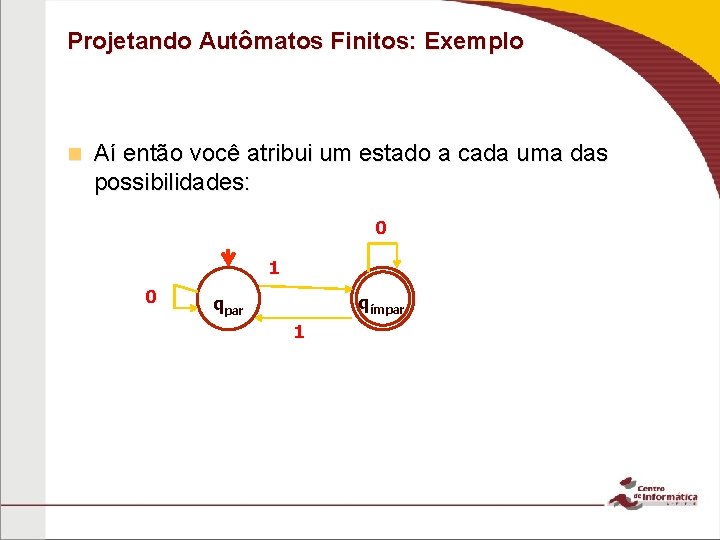
Projetando Autômatos Finitos: Exemplo n Aí então você atribui um estado a cada uma das possibilidades: 0 1 0 qímpar qpar 1

Projetando Autômatos Finitos: Outro exemplo n n n Para reconhecer a linguagem de todas as cadeias binárias que contem 001 como uma subcadeia. Você inicialmente saltaria sobre todos os 1 s. Se você chegar num 0, então você pode ter acabado de ver o primeiro dos três símbolos no padrão 001 Se nesse ponto você vê um 1, houve muito poucos 0 s, portanto você volta a saltar sobre 1 s. Mas, se você vê um 0 nesse ponto, você deve lembrar que você acabou de ver dois símbolos do padrão. Agora você precisa encontrar um 1. Se você o encontrar, logo você conseguiu achar o padrão. Continue lendo a cadeia de entrada até que o final.

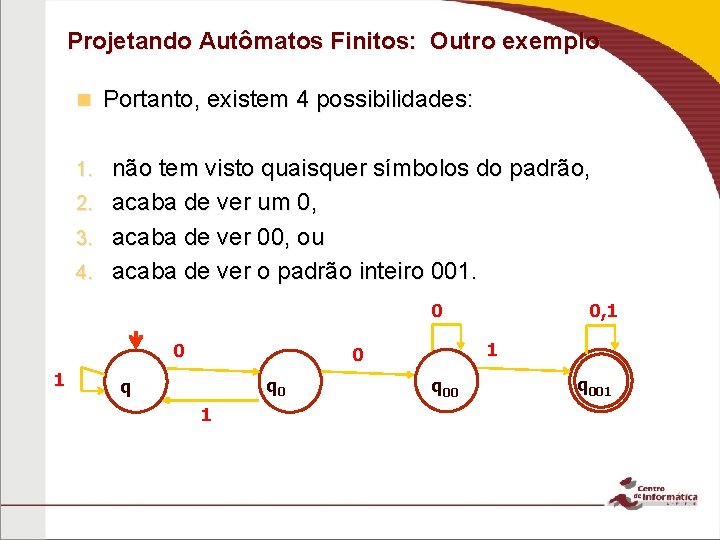
Projetando Autômatos Finitos: Outro exemplo n 1. 2. 3. 4. Portanto, existem 4 possibilidades: não tem visto quaisquer símbolos do padrão, acaba de ver um 0, acaba de ver 00, ou acaba de ver o padrão inteiro 001. 0 0 1 1 0 q 1 0, 1 q 001

PARA FIXAR n Fazer o exercício 1. 6