Arquitetura de Computadores Representao de dados 1 Arquitetura

Arquitetura de Computadores Representação de dados 1

Arquitetura de Computadores l Representação de dados: – Símbolo: marca visual ou gráfica que representa um objeto que desejamos identificar (ex: A, 1, % , . . . ) – Numeral: símbolo designado para representar um número (ex: 1, 7, 5+2, 90%, …) – Número: idéia que os símbolos representam. Um número pode ser representado por diversos numerais (ex: 5 = 7 – 2 = 4 + 1 = 10 / 2) 2 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Sistema de Numeração Posicional: – Cada algarismo componente do número têm um valor relativo conforme sua posição no número. Seu valor absoluto é modificado por um fator (peso), o qual varia conforme a posição do algarismo, sendo crescente da direita para a esquerda – Ex: Sistema de numeração decimal l 3 100, 00 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l l 4 Algarismos e Números: – Em vez de criar infinitos símbolos (algarismos) para representar cada número desejado, pode-se agrupar valores e simplificar sua representação – Ex: No base 10, até o valor 9, os números são escritos com algarismos diferentes, mas o valor seguinte, 10, é representado por 2 algarismos (1 e 0), pois não temos o algarismo “ 10” l 10 = 1 (grupo de 10 unidades) + 0 (unidades) O que fazemos para representar o valor 10 ? – Esgotadas as possibilidades com os algarismos individuais, utilizamos os 2 “menores” dígitos ou algarismos da base para representar o valor 10 – Recombinação dos algarismos da base – Pode-se usar esta recombinação para representar qualquer valor, aumentando-se apenas a quantidade de dígitos utilizados na representação – Ex: 11, 12, 13, …, 19, 20, 21, …, 29, 30, …, 99, 100, 101, …, 999, 1000, … Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores BASE: quantidade de símbolos ou dígitos ou algarismos diferentes que o referido sistema emprega para representar os números Toda a estrutura de formação dos números e realização de operações aritméticas em um sistema posicional está relacionada com o valor da BASE do referido sistema Sistema Decimal: 10 símbolos (base 10) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Sistema Binário: 2 símbolos (base 2) 0, 1 Sistema Hexadecimal: 16 símbolos (base 16) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 5 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Ex: Sistema decimal l 2622 = 2000 + 600 + 2 l 2000 600 20 2 = 2 x 1000 = 2 x 103 = 6 x 100 = 6 x 102 = 2 x 101 = 2 x 100 l l l 6 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores 7 l Neste exemplo o fator (peso) que modifica o valor do algarismo conforme sua posição, é, em cada parcela, uma potência de 10 (1000, 10 e 1) a partir da potência 0 (algarismo mais à direita do número, ou menos significativo), sendo crescente para a esquerda (potência 1, potência 2, …) até o último algarismo (mais significativo) l É um potência de 10 porque o sistema usado como exemplo é o sistema DECIMAL. Isso conduz a um conceito fundamental dos sistemas posicionais: o de BASE Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Algarismos e Números: – Qualquer número pode ser interpretado como tendo um VALOR dado pela seguinte expressão: – – – 8 onde: k = base do sistema bi = um algarismo da base n = quantidade de algarismos inteiros no número m = quantidade de algarismos fracionários número Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Ex: 541. 2510 = 5 102 + 4 101 + 1 100 + 2 10 -1 + 5 10 -2 = (500)10 + (40)10 + (1)10 + (2/10)10 + (5/100)10 = (541. 25)10 l 9 Onde temos: – k = base do sistema = 10 – bi(s) = algarismos = 5, 4, 1, 2, 5 – n = qtd algarismos inteiros = 3 – m = qtd algarismos fracionários = 2 Professor: Arlindo Tadayuki Noji (5, 4, 1) (2, 5) Instituto de Ensino Superior

Arquitetura de Computadores l 10 Representação numérica para computador: – Toda informação humana pode ser bem representada com zeros e uns. – Existem vários tipos de representações que de uma mesma informação. Ex: 10 d = 1010 b = 0 Ah = 12 o =. . . – Os seres humanos tem facilidades para entender o formato decimal – As máquinas tem facilidades para entender o formato Numérico Binário Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l 11 Limites computacionais – A arquitetura de um computador define o número de bits que o um processador pode usar para calcular valores. Este número de bits pode limitar a quantidade de dados que poderão ser processados, se as informações forem muito grandes. – Uma outra situação comum é que os operando podem não exceder os limites, mas os resultados podem, gerando um overflow. – Ex: em 8 bits é facil somar 100 + 100 = 200 d, mas 100 x 100 = 10000 (Overflow) Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l 12 Números de Ponto Fixo – Os números de ponto fixo, são representados sempre com número de dígitos fixo, com uma virgula em posição fixa em relação ao número. Ex: 0, 23 5, 34 9, 11 – Podemos representar também como números binários: Ex: 11, 00 01, 11 11, 11 – A virgula não existe nos computadores, apenas na cabeça dos programadores. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Intervalo de Representação e Precisão numérica de ponto fixo – – – 13 Uma representação de ponto fixo pode ser caracterizada pelo intervalo de representação de números que podem ser expressos. (a distância entre maior e o menor número) A precisão é dada pela distância entre dois números adjacentes. Exemplo de Intervalo: 0, 00 pode ir até 9, 99, logo é denotado como [0, 00 , 9, 99] Exemplo de Precisão: 9, 98 e 9, 99, a diferença é 0, 01, logo a precisão é de 0, 01 Exemplo de Erro: o erro é a precisão/2, logo é 0, 005. Professor: Arlindo Tadayuki Noji Figura retirada do livro Introdução a Arquitetura de Computadores, Miles J. Murdocca Instituto de Ensino Superior

Arquitetura de Computadores l Outras formas de representações – – l l 14 [0, 00 , 9, 99] , [00, 0 , 99, 9] , [000, 999] ou [-49, 50] , [ -99, 0] Representações e precisão pontos importantes em arquitetura de computadores porque ambos são finitos ma implementação da arquitetura. Problema: No mundo real, os números são infinitos. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Lei associativa da álgebra nem sempre funciona em computadores – A + (B + C) = (A + B) + C – Se o intervalo numérica for de [-9 , 9 ] e sendo a = 7, b = 4 e c = -3, então: l l 15 A + (B + C) = 7 + (4 – 3) = 8 (A + B) + C = (7 + 4) – 3) = - 2 ( Overflow) Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

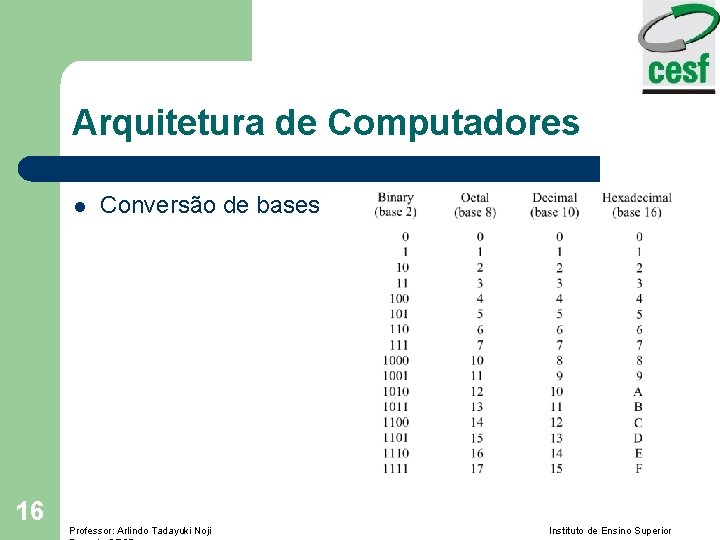
Arquitetura de Computadores l 16 Conversão de bases Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores • Convertendo números de pontos fixos: l Exemplo: Convertendo 23, 37510 para base binária – 17 A conversão é feita em 2 etapas: l Parte INTEIRA + parte FRACIONÁRIA (se houver) l PARTE INTEIRA: Continuação – Em cada divisão, o resto encontrado é um algarismo significativo do número na nova base – O primeiro resto encontrado é o valor do algarismo menos significativo (mais à direita) e o último será o algarismo mais significativo (mais à esquerda) – Toda a aritmética envolvida no cálculo é da base de origem (neste caso, base 10) – Utilizar uma tabela de equivalência dos algarismos das bases K e 10, para saber como representar os algarismos encontrados (resto), se necessário, na base K Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l 18 Parte Inteira Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l 19 Parte Fracionária Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Portanto, para representar um número na base 10 em uma base qualquer K, converte-se primeiro a parte inteira, depois a parte fracionária, e utiliza-se ambas na notação “Inteiro , Fração” – Logo: – – 20 Professor: Arlindo Tadayuki Noji 23, 375 = ( )2 23 = 10111 0, 375 = 0, 011 23, 375 = 10111, 011 Instituto de Ensino Superior

Arquitetura de Computadores l Base 10 para Base K: PARTE FRACIONÁRIA: Método de Multiplicações Sucessivas • Ex 2: Nem sempre pode-se converter uma fração finita em outra base 21 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Base K para Base 10: – Ex 1: 100011, 012 = 20 + 35, 2510 – Ex 2: 6738 = 22 Professor: Arlindo Tadayuki Noji 100011, 012 = ( ) 10 1 25 + 0 24 + 0 23 + 0 22 + 1 21 + 1 0 2 -1 + 1 2 -2 = 32 + 1 + 0, 25 = 6738 = ( ) 10 6 82 + 7 81 + 3 80 = 384 + 56 + 3 = 44310 Instituto de Ensino Superior

Arquitetura de Computadores l 23 Soma Binária Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

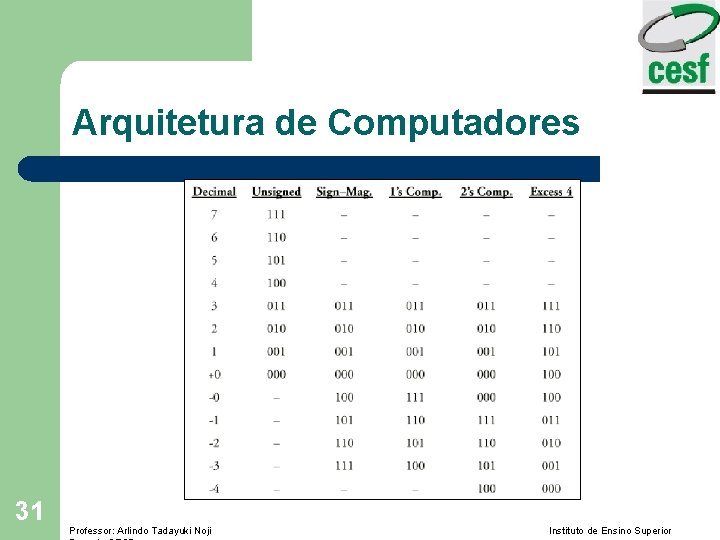
Arquitetura de Computadores l Representação numérica sinalizado – – – Para um número binário de 8 bits, temos 256 possibilidades. Se temos que representar os números negativos também, devemos separar uma parte destas possibilidades para representar estes números. Temos 4 principais formas de sinalizar um número negativo: l l 24 Sinal de Magnetude Complemento de um Complemento de dois Excesso de 4. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Magnetude de sinal – – Basta colocar o bit mais significativo com o sinal 1, para representar um número negativo Exemplo: +2510 = 000110012 -2510 = 10012 25 – Duas representações de Zeros. Ex: 0000 e 10000000 – Intervalos de números de +127 e – 127 em decimal Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Complemento de um Os bits são trocados, os Zeros se tornam Um e os Uns se tornam Zeros. – Exemplo: +2510 = 000110012 – -2510 = 111001102 26 – Possui duas representação de zeros: +0 = 00002, -0 = 11112. – Faixa de valores: +12710, e o menor número -12710, usando 8 bits de representação Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Complemento de dois – – Neste modo de representação, é executado o complemento de um, mais a somatória de 1. Exemplo: +2510 = 000110012 -2510 = 111001112 Apenas uma representação numérica do Zero: +0 = 00002, -0 = 00002. Faixa de valores: +12710, e o menor número é -12810, para 8 bits. 27 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Representação de Excesso – – O número é tratado sem sinal, então o valor é deslocado (shifted) do mesmo. Exemplo: (para criar um numero de excesso, basta somar 128 ao número em um padrão de 8 bits) +1210 = 100011002 -1210 = 011101002 28 – Ünica representação do Zero – Maior número é +12710, enquanto que o menor número é -12810, usando 8 -bit de representação Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Representação de Decimal em Binário – – – 29 Números podem ser representados em base 10, mesmo usando codificação binária. Cada dígito na base 10 ocupa quatro bits, o que é conhecido como decimal codificado em binário (BCD). Então, cada dígito utiliza os primeiros 10 padrões de binários de 4 dígitos. Ex: 123 -> 0001 0010 0011 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l 30 Complemento de 9 e 10 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores 31 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Número de Pontos Flutuantes – – Permite que grandes números e pequenos números possam ser representados usando somente poucos dígitos, de acordo com a precisão especificada. A precisão é determinada pela quantidade de dígitos da fração (inclui a parte inteira e fracionária) e o dimensão do número é determinado pelo número de dígitos do campo expoente. • Examplo (+6. 023 1023): 32 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Normalização – – 33 Um número na base 10, digamos 254 pode ser representada em ponto flutuante na forma de 254 x 100 , ou equivalentemente: l 25. 4 x 101, ou l 2. 54 x 102, ou l . 254 x 103, ou l . 0254 x 104, ou l Ou de outras formas infinitas, que podem gerar problemas na hora de comparar dois números. Devido a este problema, os números de ponto flutuante são normalizados. Normalmente, mas nem sempre os números são deslocados para a esquerda logo após a virgula. Ex: . 254 103. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Exemplo de ponto flutuante – – Vamos representar o número. 254 x 10 3 numa base normalizada de base 8, com bit de sinal e 3 bits de excesso de 4 para o expoente. Passo 1, converter a base l . 254 103 = 25410. Usando o método já conhecido, temos 25410 = 376 80: 254/8 = 31 R 6 31/8 = 3 R 7 3/8 = 0 R 3 – – Passo 2, normalizar: 376 80 =. 376 83. Passo 3: Preencher os campos de bits, com o sinal, expoente de 3+4 = 7 (excesso ed 4) e 4 dígitos para fração =. 3760: 0 111. 011 110 000 34 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l No exemplo anterior temos – – – l Com estes parametros é possivel calcular os seguintes valores: – – – 35 base = 8; S = 4; M=3; M = -4 Representação do Zero = 0 000 000 000; Maior número representável Menor número representável O maior GAP entre dois números O menor GAP entre dois números O total de bits que são necessários para representar o número Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l 36 Erros, faixas e precisões: – Maior número representável: b. M (1 - b-s) = 83 (1 - 8 -4) – Menor número representável: bm b-1 = 8 -4 - 1 = 8 -5 – Maior Gap: b. M b-s = 83 - 4 = 8 -1 – Menor Gap: bm b-s = 8 -4 - 4= 8 -8 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Erros, faixas e precisões: – Cálculo de números de representação l Há 5 componentes: – – – l 37 (A) O sinal de bits: 2 x (B) expoente: (M-m) + 1 (C) Valor do primeiro dígito: b – 1 (Não pode ser Zero para primeiro dígito normalizado) (D) Valor de cada um dos s-1 digitos restantes: Bs-1 (E) representação especial para Zero: + 1 Para este exemplo, temos: 2 ((3 - 4) + 1) (8 - 1) 84 -1 + 1 = número que podem ser representados (quantidade de padrões). Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Exemplo de Ponto Flutuante: – – – 38 Menor número: 1/8 Maior número: 7/4 Menor gap: 1/32 Maior gap: ¼ Quantidades de números representáveis: 33 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l l 39 O erro relativo é aproximadamente o mesmo para todos os número Se pegarmos a razão entre o maior gap com o maior número e comparar com a razão do menor gap com o menor número, teremos o mesmo valor. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Conversão de números – – – : – – Converter (9. 375 10 -2)10 na base 2 da notação científica Tirar a notação científica: . 09275 Converter em notação binária. 09375. 1875 2 2 = = 0. 1875 0. 375 2 = 0. 75 2 = 1. 0 Portanto: (. 09375)10 = (. 00011)2. Finalmente converter para a base 2 normalizada: . 00011 =. 00011 20 = 1. 1 2 -4 40 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

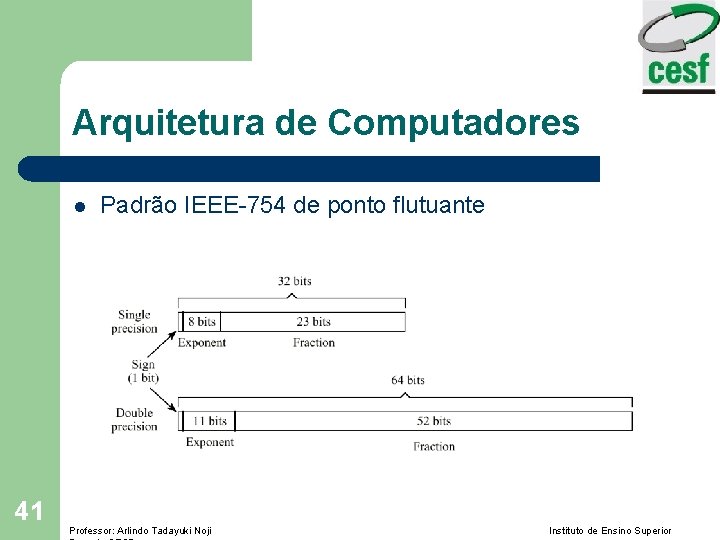
Arquitetura de Computadores l 41 Padrão IEEE-754 de ponto flutuante Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

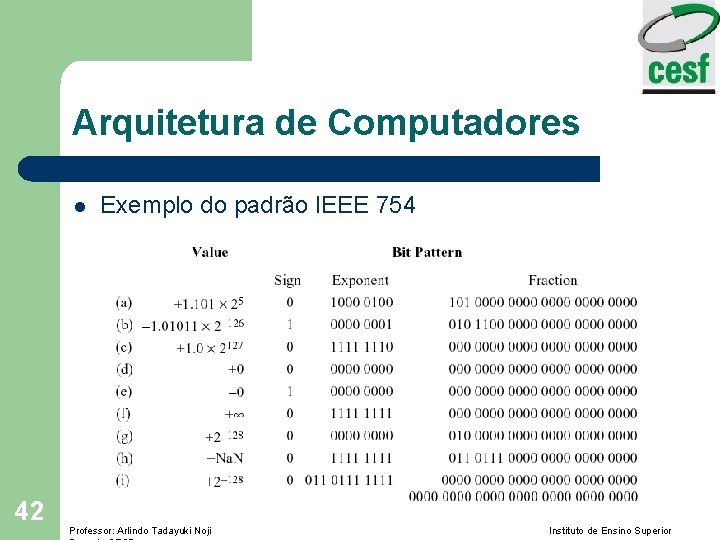
Arquitetura de Computadores l 42 Exemplo do padrão IEEE 754 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Exemplo de uso do padrão IEEE 754 – Representar -12. 625 na precisão simples do formato IEEE-754: l Passo 1: Converter para a base 2: -12. 62510 = -1100. 1012 l Passo 2: Normalizar: -1100. 1012 = -1. 1001012 23 l Passo 3: Preencher os campos de bits: Sinal negativo, usar 1 – Expoente em excesso de 127 (não usar 128). O expoente é representado por um inteiro náo sinalizado: 3 + 127 = 130. – O bit 1 mais significativo é escondido. – 1 1000 0010. 1001 0100 0000 000 43 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

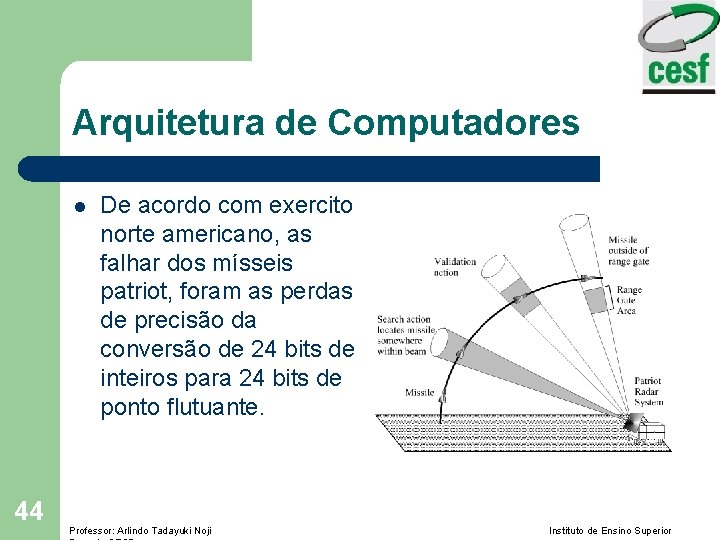
Arquitetura de Computadores l 44 De acordo com exercito norte americano, as falhar dos mísseis patriot, foram as perdas de precisão da conversão de 24 bits de inteiros para 24 bits de ponto flutuante. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

Arquitetura de Computadores l Tabela ASCII – – 45 A possui o valor de 41 h. Para converter em maiuscula, basta somar 20 h O caracter 5 tem o valor de 35 h, para converter para numero, basta subtrair de 30 h. Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

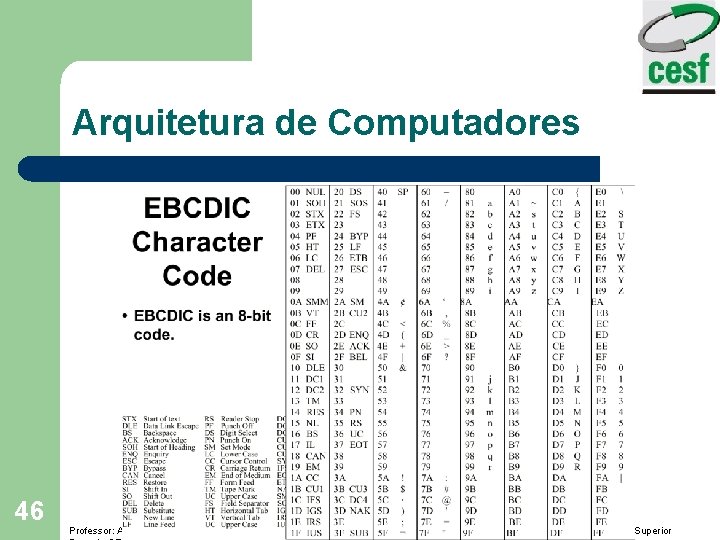
Arquitetura de Computadores 46 Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior

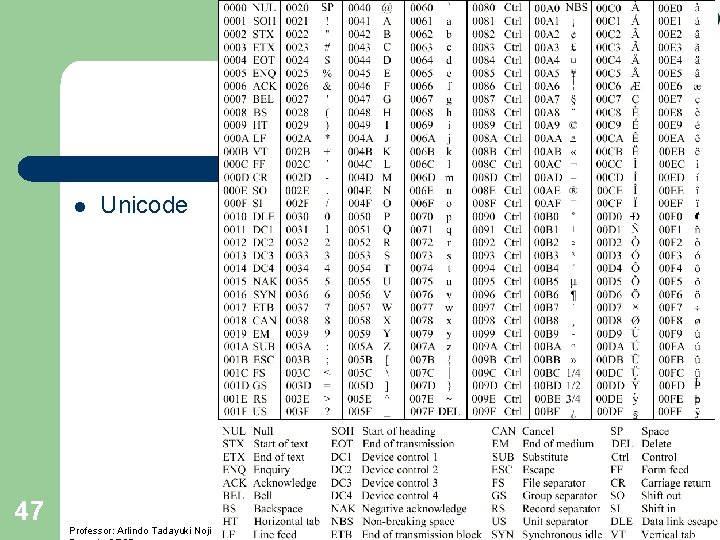
l 47 Unicode Professor: Arlindo Tadayuki Noji Instituto de Ensino Superior