Aritmetizacin de las reas LA FRMULA DE HERN

Aritmetización de las áreas LA FÓRMULA DE HERÓN

O como convertirte en un(a) agrimensor(a)

Conceptos… El área es una medida de la extensión de una superficie, expresada en unidades de medida denominadas Unidades de Superficie. Para superficies planas el concepto es más intuitivo. Cualquier superficie plana de lados rectos (polígonos) se puede triangular y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie como variedad bidimensional) y la magnitud métrica (área) asociada al concepto geométrico. Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial. Para poder definir el área de una superficie en general –que es un concepto métrico–, se tiene que haber definido un tensor métrico sobre la superficie en cuestión: cuando la superficie está dentro de un espacio euclídeo, la superficie hereda una estructura métrica natural inducida por la métrica euclídea.

… y disquisiciones. Conviene diferenciar entre: SUPERFICIE es una variedad bidimensional del espacio n-dimensional. De forma más llana: aquello que sólo tiene longitud y anchura. EXTENSIÓN es una propiedad de las superficies cerradas que permite compararlas unas con otras. Es, pues, medible. ÁREA es la medida de la extensión de una superficie cerrada, y su valor depende de la unidad de medida elegida. MEDIR es comparar la cantidad desconocida queremos determinar y una cantidad conocida de la misma magnitud, que elegimos como unidad, para determinar cuántas veces la contiene. Al resultado de medir se le denomina MEDIDA. Dos figuras son EQUIVALENTES si tienen la misma área.

Historia de un LOGRO La idea de que el área es la medida que proporciona el tamaño de la región encerrada en una figura geométrica proviene de la antigüedad. En el Antiguo Egipto, tras la crecida anual de río Nilo inundando los campos, surge la necesidad de calcular el área de cada parcela agrícola para restablecer sus límites; para solventar eso, los egipcios inventaron la geometría, según Heródoto. El manera de calcular el área de un polígono como la suma de las áreas de los triángulos, es un método que fue propuesto por primera vez por el sabio griego Antifón hacia el año 430 a. C. Hallar el área de una figura curva entraña más dificultad. El método de agotamiento consiste en inscribir y circunscribir polígonos en la figura geométrica, aumentar el número de lados de dichos polígonos y hallar el área buscada. Con este sistema que se conoce como método exhaustivo de Eudoxo, se consiguió obtener una aproximación para calcular el área de un círculo. Dicho sistema fue empleado tiempo después por Arquímedes para resolver otros problemas similares, así como el cálculo aproximado del número π.

Unidad de Medida de Superficies Para ESTABLECER una unidad de medida hay que determinar su: FORMA: tiene que teselar (llenar sin huecos) la superficie, en este caso (para simplificar) plana. Entre las muchas formas que llenan el plano escogemos la cuadrada porque queremos. TAMAÑO: nuestro Sistema de Medida es Métrico y Decimal. Es decir, se basa en el metro, por eso es natural tomar la unidad de superficie de un metro de lado. 1 m NOMBRE: cuadrada y de un metro de lado, pues Metro Cuadrado, cuyo símbolo es m 2.

El proceso de la MEDIDA… Medir el área de una fígura es contar cuántas unidades de superficie contiene. Pero este proceso resulta muy complicado en casi todas las ocasiones, así que vamos a deducir FÓRMULAS que nos permitan CALCULAR el área de una figura a partir de sus ‘dimensiones’

…de Figuras Planas Cerradas. En el plano se puede distinguir entre una infinidad de figuras que tienen formas, tamaños y posiciones particulares sobre un plano. Podemos diferenciar entre las figuras de una sola dimensión llamadas curvas y las de dos dimensiones. El término curva no se define y se usa para describir figuras en el plano. En las curvas podemos distinguir entre las curvas abiertas, las curvas cerradas simples y las curvas cerradas no simples. Una curva es abierta si se traza de forma continua y su punto inicial es distinto de su punto final. Las curvas cerradas son aquellas que se trazan de forma continua y su punto inicial es igual a su punto final. Una curva simple abierta es aquella que su trazado es continuo, no tiene puntos de intersección y sus puntos inicial y final son diferentes. Si una curva tiene al menos un punto de intersección decimos que es una curva no simple. Un polígono es una curva simple cerrada compuesta por segmentos consecutivos de líneas rectas. Los segmentos de línea se llaman lados y los puntos de intersección de los segmentos se llaman vértices. Los nombres de los polígonos se asignan de acuerdo al número de lados de la figura. Un polígono de n lados se llama n-ágono.

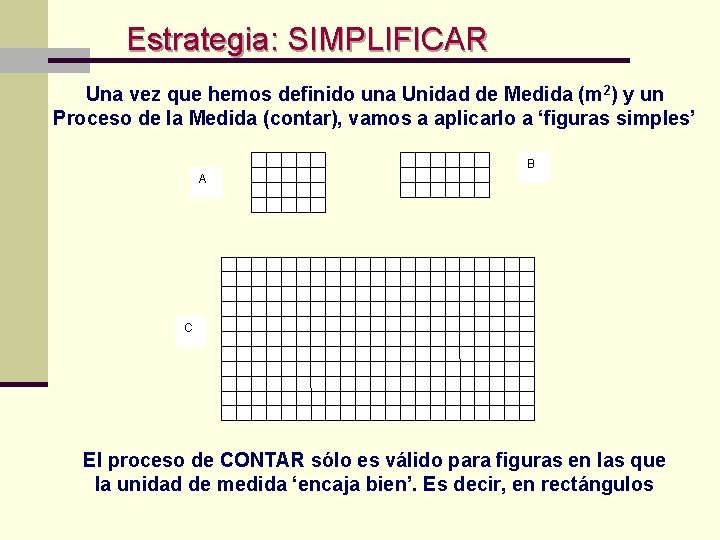
Estrategia: SIMPLIFICAR Una vez que hemos definido una Unidad de Medida (m 2) y un Proceso de la Medida (contar), vamos a aplicarlo a ‘figuras simples’ B A C El proceso de CONTAR sólo es válido para figuras en las que la unidad de medida ‘encaja bien’. Es decir, en rectángulos

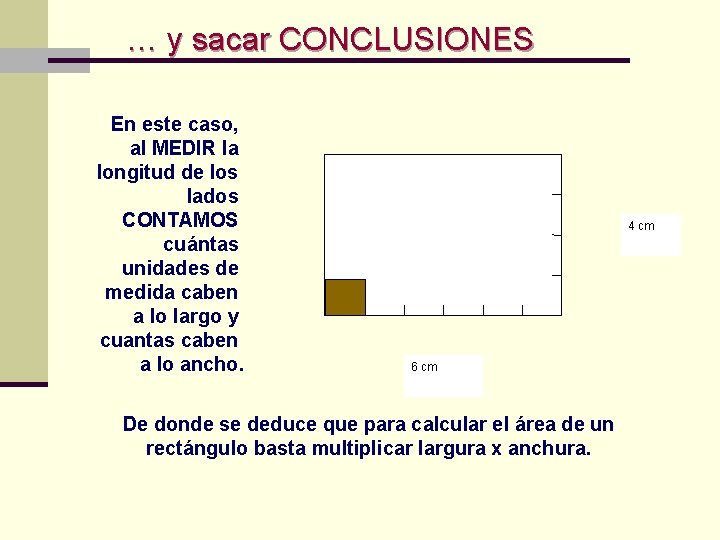
… y sacar CONCLUSIONES En este caso, al MEDIR la longitud de los lados CONTAMOS cuántas unidades de medida caben a lo largo y cuantas caben a lo ancho. 4 cm 6 cm De donde se deduce que para calcular el área de un rectángulo basta multiplicar largura x anchura.

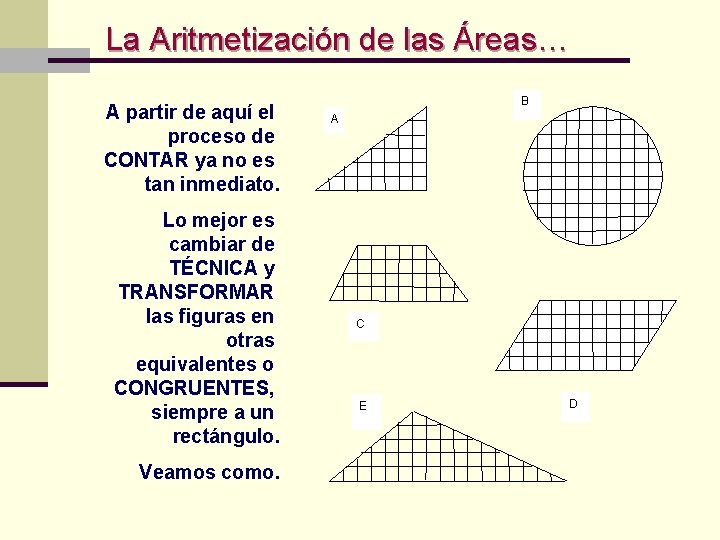
La Aritmetización de las Áreas… A partir de aquí el proceso de CONTAR ya no es tan inmediato. Lo mejor es cambiar de TÉCNICA y TRANSFORMAR las figuras en otras equivalentes o CONGRUENTES, siempre a un rectángulo. Veamos como. B A C E D

… consiste en deducir FÓRMULAS Paralelogramo h b Triángulo h b

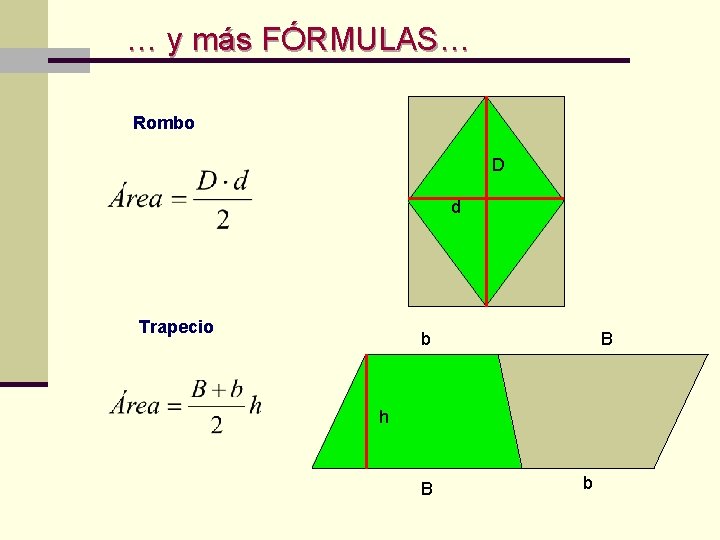
… y más FÓRMULAS… Rombo D d Trapecio b B h B b

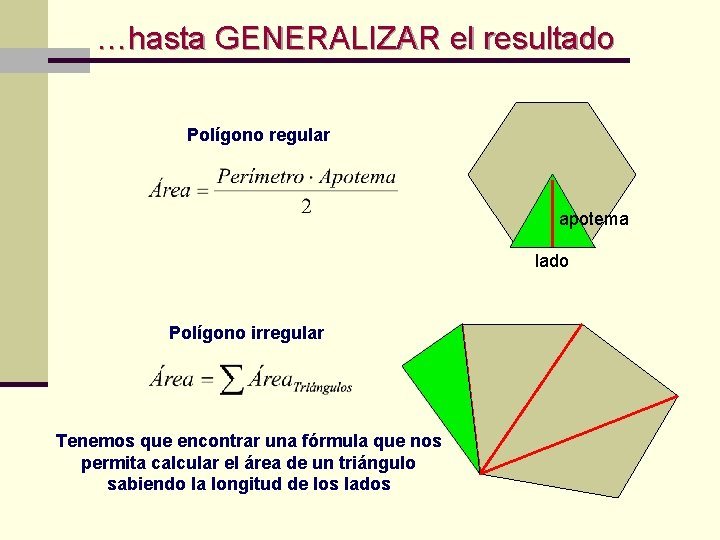
…hasta GENERALIZAR el resultado Polígono regular apotema lado Polígono irregular Tenemos que encontrar una fórmula que nos permita calcular el área de un triángulo sabiendo la longitud de los lados

La Fórmula de Herón… En geometría, la fórmula de Herón relaciona el área de un triángulo en términos de las longitudes de sus lados a, b y c: donde s es el semiperímetro del triángulo: La fórmula también puede escribirse de las siguientes formas: La fórmula de Herón se distingue de otras fórmulas para hallar el área de un triángulo, como la de la mitad de la base por la altura o la de la mitad del módulo de un producto cruz de dos lados, al no requerir ninguna elección arbitraria de un lado como base o un vértice como origen.

… tiene una Historia. La fórmula se le atribuye a Herón de Alejandría, y se puede encontrar una prueba en su libro, Métrica, escrito en el 60 d. C. Se ha propuesto que Arquímedes ya sabía la fórmula dos siglos antes, y puesto que Métrica es una colección de los conocimientos matemáticos disponibles en el mundo antiguo, es posible que la fórmula preceda a la referencia que figura en dicho trabajo. A saber, una fórmula equivalente a la de Herón: , donde fue descubierta por los chinos, independientemente de los griegos. Fue publicada en Shushu Jiuzhang ("Tratado matemático en nueve secciones"), escrito por Qin Jiushao y publicado en el año 1247.

La DEMOSTRACIÓN de la Fórmula… b h a c 2 h 2 a Dado un triángulo cualquiera de lados a, b y c, tomemos la altura h sobre a. Esto nos permite montar la siguiente figura.

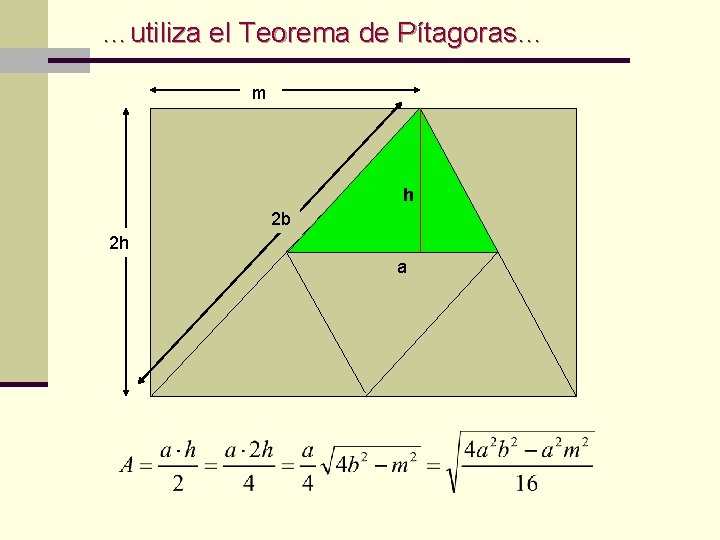
…utiliza el Teorema de Pítagoras… m h 2 b 2 h a

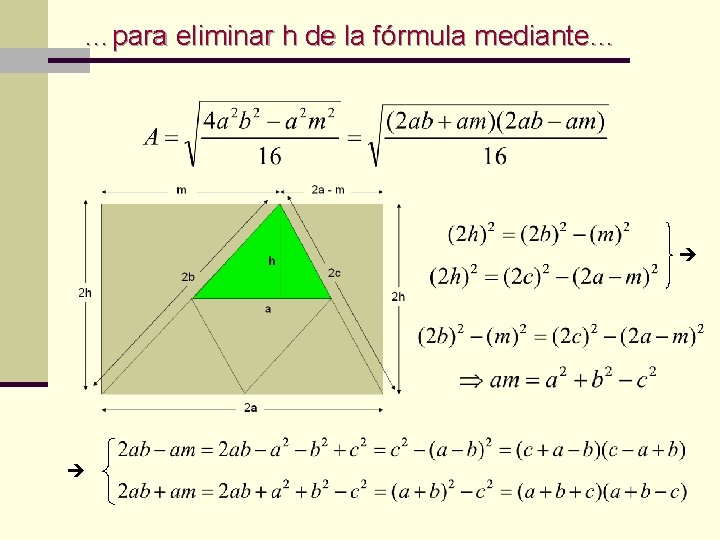
…para eliminar h de la fórmula mediante…

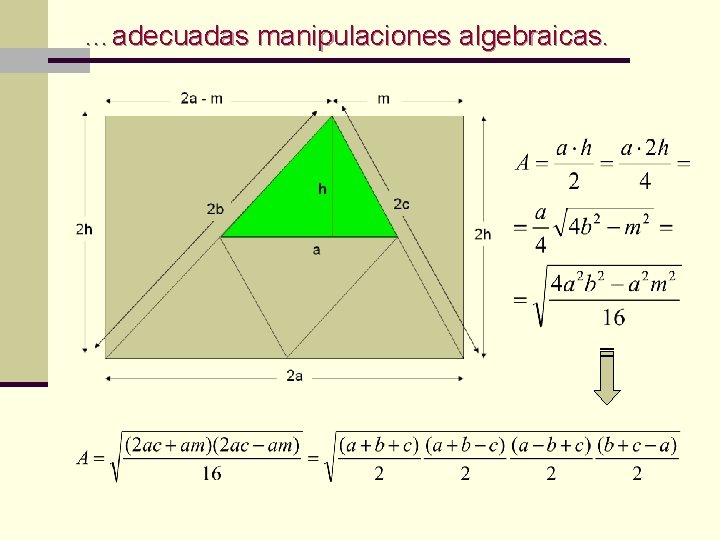
…adecuadas manipulaciones algebraicas.

Obteniendo, así, la ansiada fórmula … donde es el semiperímetro Cuya importancia radica en que es una fórmula que sólo depende de la longitud de los lados, fáciles de medir en todas las ocasiones.

…que es un CASO PARTICULAR. La fórmula de Herón es un caso particular de la fórmula de Brahmagupta para el cálculo del área de cuadriláteros inscritos en una circunferencia; y ambas son casos particulares de la fórmula de Bretschneider para calcular área de un cuadrilátero. Expresando parte de la fórmula de Herón (sólo los términos internos a la raíz) de forma matricial dentro de un determinante (determinante de Cayley-Menger) en términos de cuadrados de distancias de los tres vértices dados (más precisamente, el valor absoluto del determinante), obtenemos: Donde a, b y c son las longitudes de los lados del triángulo y A será el área del mismo.

Figuras planas cerradas no poligonales Un círculo, en geometría euclídea, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida. En castellano, la palabra círculo tiene varias acepciones, y se utiliza indistintamente círculo por circunferencia, que es la curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud (es decir, el perímetro del círculo) Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie).

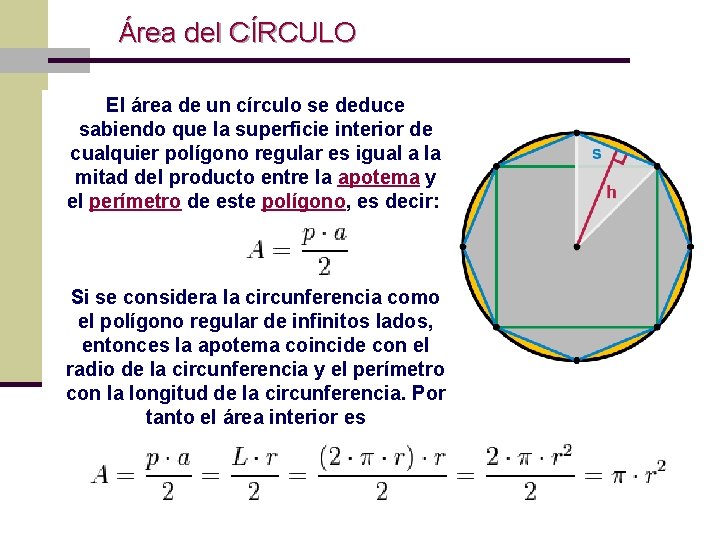
Área del CÍRCULO El área de un círculo se deduce sabiendo que la superficie interior de cualquier polígono regular es igual a la mitad del producto entre la apotema y el perímetro de este polígono, es decir: Si se considera la circunferencia como el polígono regular de infinitos lados, entonces la apotema coincide con el radio de la circunferencia y el perímetro con la longitud de la circunferencia. Por tanto el área interior es

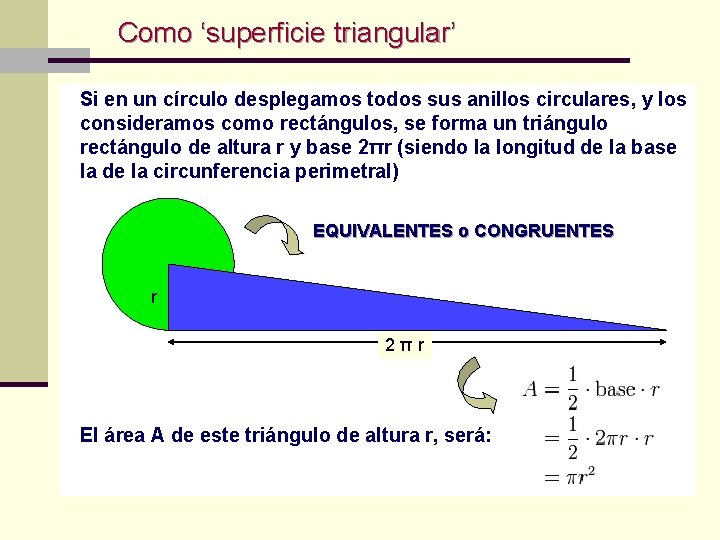
Como ‘superficie triangular’ Si en un círculo desplegamos todos sus anillos circulares, y los consideramos como rectángulos, se forma un triángulo rectángulo de altura r y base 2πr (siendo la longitud de la base la de la circunferencia perimetral) EQUIVALENTES o CONGRUENTES r 2πr El área A de este triángulo de altura r, será:

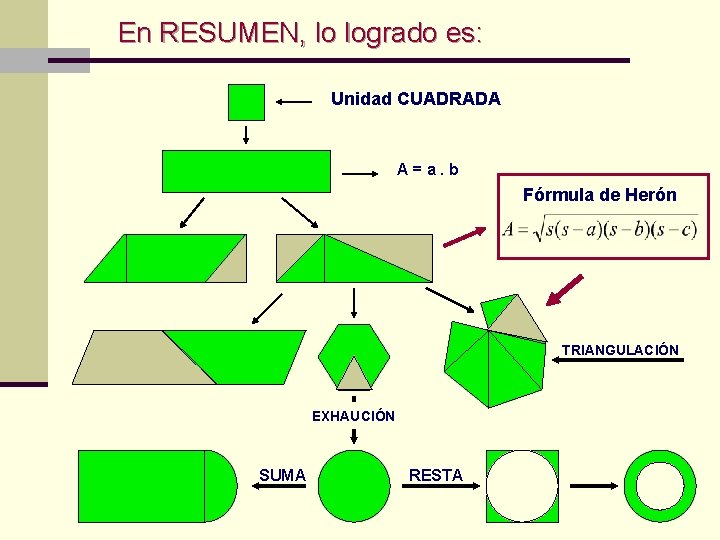
En RESUMEN, lo logrado es: Unidad CUADRADA A = a. b Fórmula de Herón TRIANGULACIÓN EXHAUCIÓN SUMA RESTA

Para seguir avanzando… Como hemos visto, en geometría elemental se deducen fórmulas para las área de muchas figuras planas, pero un poco de reflexión hace ver que raramente se da una definición aceptable de área. El área de una región se define a veces como el número de cuadrados de lado unidad que caben en una región, pero por ejemplo el círculo de radio unidad tiene por área el número irracional π, pero no está claro cual es el significado de π cuadrados. En general se tiene la percepción intuitiva de que una región contenida dentro de una curva cerrada posee un "área" la cual mide el número de unidades cuadradas dentro de la curva. Las propiedades básicas del área que la intuición sugiere son: 1. El área es un número (positivo, dependiente de la elección de la unidad de longitud) 2. Este número es el mismo para figuras congruentes o equivalentes. 3. Para todos los rectángulos el área es el producto de las longitudes de los lados adyacentes, es decir, de sus dimensiones. 4. Para una región descompuesta en secciones el área total es igual a la suma (o resta) de las áreas de las secciones. Una consecuencia inmediata es el hecho de que para una región A que es parte de una región B, el área de A no puede ser mayor que el área de B.

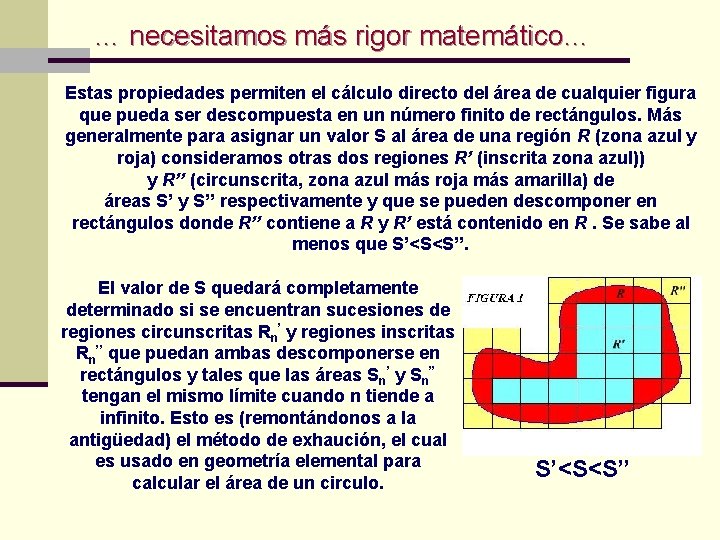
… necesitamos más rigor matemático… Estas propiedades permiten el cálculo directo del área de cualquier figura que pueda ser descompuesta en un número finito de rectángulos. Más generalmente para asignar un valor S al área de una región R (zona azul y roja) consideramos otras dos regiones R’ (inscrita zona azul)) y R’’ (circunscrita, zona azul más roja más amarilla) de áreas S’ y S’’ respectivamente y que se pueden descomponer en rectángulos donde R’’ contiene a R y R’ está contenido en R. Se sabe al menos que S’<S<S’’. El valor de S quedará completamente determinado si se encuentran sucesiones de regiones circunscritas Rn’ y regiones inscritas Rn’’ que puedan ambas descomponerse en rectángulos y tales que las áreas Sn’ y Sn’’ tengan el mismo límite cuando n tiende a infinito. Esto es (remontándonos a la antigüedad) el método de exhaución, el cual es usado en geometría elemental para calcular el área de un circulo. S’<S<S’’

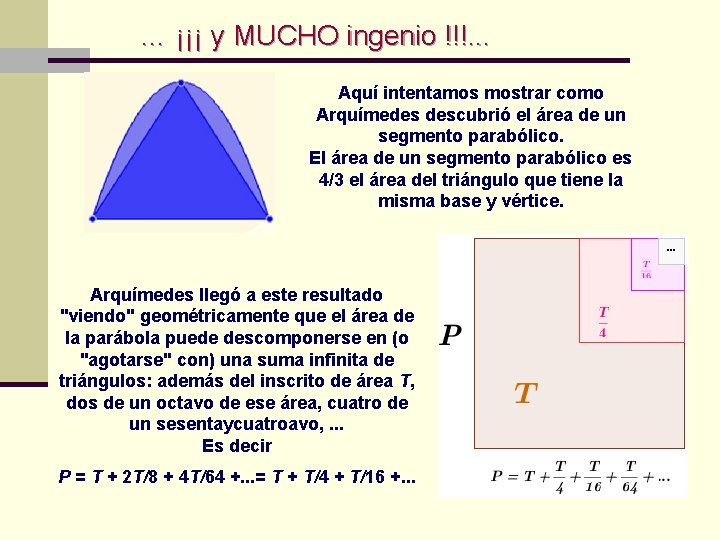
… ¡¡¡ y MUCHO ingenio !!!. . . Aquí intentamos mostrar como Arquímedes descubrió el área de un segmento parabólico. El área de un segmento parabólico es 4/3 el área del triángulo que tiene la misma base y vértice. Arquímedes llegó a este resultado "viendo" geométricamente que el área de la parábola puede descomponerse en (o "agotarse" con) una suma infinita de triángulos: además del inscrito de área T, dos de un octavo de ese área, cuatro de un sesentaycuatroavo, . . . Es decir P = T + 2 T/8 + 4 T/64 +. . . = T + T/4 + T/16 +. . .

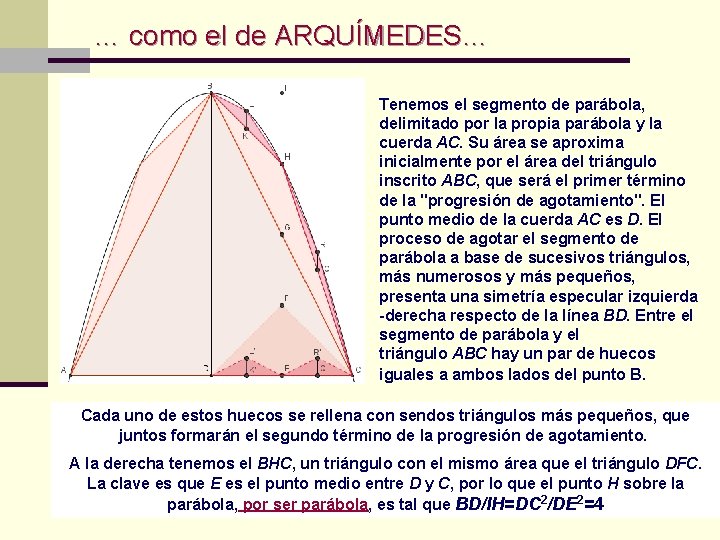
… como el de ARQUÍMEDES… Tenemos el segmento de parábola, delimitado por la propia parábola y la cuerda AC. Su área se aproxima inicialmente por el área del triángulo inscrito ABC, que será el primer término de la "progresión de agotamiento". El punto medio de la cuerda AC es D. El proceso de agotar el segmento de parábola a base de sucesivos triángulos, más numerosos y más pequeños, presenta una simetría especular izquierda -derecha respecto de la línea BD. Entre el segmento de parábola y el triángulo ABC hay un par de huecos iguales a ambos lados del punto B. Cada uno de estos huecos se rellena con sendos triángulos más pequeños, que juntos formarán el segundo término de la progresión de agotamiento. A la derecha tenemos el BHC, un triángulo con el mismo área que el triángulo DFC. La clave es que E es el punto medio entre D y C, por lo que el punto H sobre la parábola, por ser parábola, es tal que BD/IH=DC 2/DE 2=4

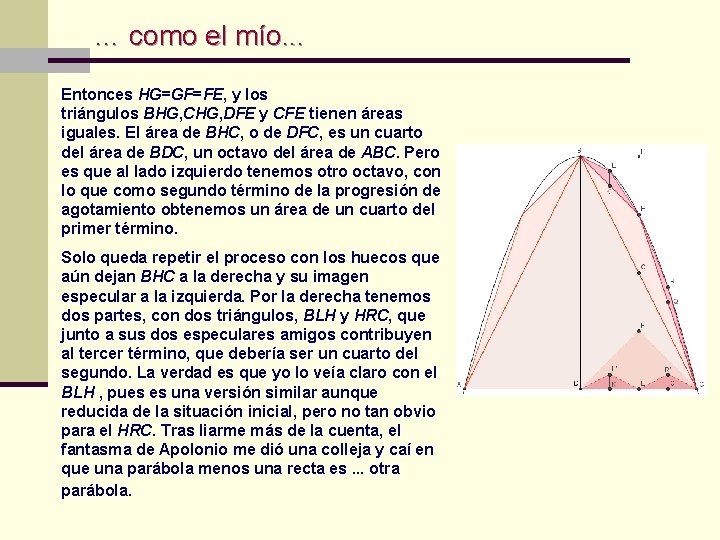
… como el mío. . . Entonces HG=GF=FE, y los triángulos BHG, CHG, DFE y CFE tienen áreas iguales. El área de BHC, o de DFC, es un cuarto del área de BDC, un octavo del área de ABC. Pero es que al lado izquierdo tenemos otro octavo, con lo que como segundo término de la progresión de agotamiento obtenemos un área de un cuarto del primer término. Solo queda repetir el proceso con los huecos que aún dejan BHC a la derecha y su imagen especular a la izquierda. Por la derecha tenemos dos partes, con dos triángulos, BLH y HRC, que junto a sus dos especulares amigos contribuyen al tercer término, que debería ser un cuarto del segundo. La verdad es que yo lo veía claro con el BLH , pues es una versión similar aunque reducida de la situación inicial, pero no tan obvio para el HRC. Tras liarme más de la cuenta, el fantasma de Apolonio me dió una colleja y caí en que una parábola menos una recta es. . . otra parábola.

… ¡¡¡ y como el TUYO !!! En esta figura restando de la parábola azul la recta AC también azul, nos queda la versión "derecha“, es decri, la parábola roja con la cuerda horizontal como base del segmento. Esto de paso sirve para comprender que el segmento parabólico y el triángulo inscrito pueden no estar derechos, como los azules, y que esa situación más general es reducible a la de segmentos de parábola derechos, como el rojo. El vértice de la parábola roja queda en la vertical del punto B de tangencia a la parábola azul de la paralela a la cuerda AC. En la parábola azul, esta cuerda AC y la cuerda infinita que parte de B y pasa por D son conjugadas, es decir, BD∞corta por el punto medio a todas las cuerdas paralelas a AC, aunque estas cuerdas no hagan en este caso lo recíproco. Siempre la cuerda conjugada infinita es paralela al eje de la parábola.