Aristotle University of Thessaloniki Department of Geodesy and

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and reception

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Monochromatic (sinusoidal) signals Monochromatic

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase at an

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase Φ=0 Φ

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t

Aristotle University of Thessaloniki – Department of Geodesy and Surveying General form of a

Aristotle University of Thessaloniki – Department of Geodesy and Surveying transmitter r A. Dermanis

Aristotle University of Thessaloniki – Department of Geodesy and Surveying transmitter r =0 Epoch

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy :

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy spectral density of

Aristotle University of Thessaloniki – Department of Geodesy and Surveying The electromagnetic spectrum visible

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power :

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of

Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem A.

Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem Representation

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Φίλτρα = χρονικά αμετάβλητα

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : A.

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : when

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth A. Dermanis Signals

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth Low Pass Filter

Aristotle University of Thessaloniki – Department of Geodesy and Surveying END A. Dermanis Signals

Slides: 134

Download presentation

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signals and Spectral Methods in Geoinformatics Lecture 5: Signals – General Characteristics A. Dermanis Signals and Spectral Methods in Geoinformatics

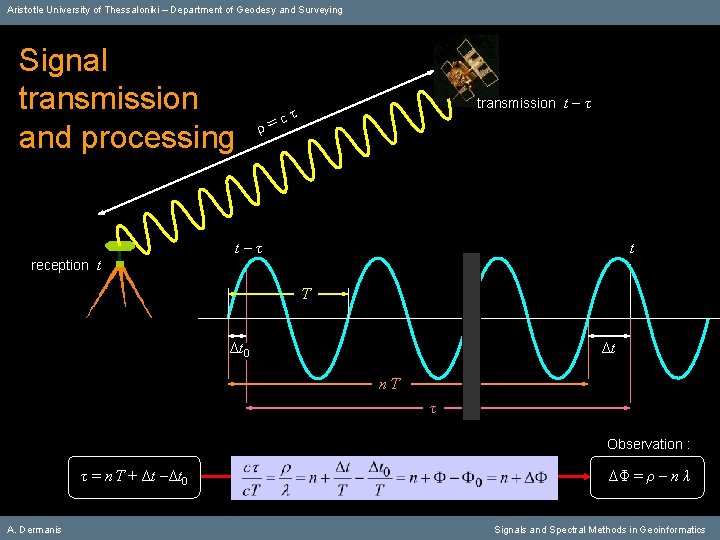
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and processing reception t ρ= transmission t τ cτ t Τ Δt 0 Δt nΤ τ Observation : τ = n Τ + Δt –Δt 0 A. Dermanis ΔΦ = ρ – n λ Signals and Spectral Methods in Geoinformatics

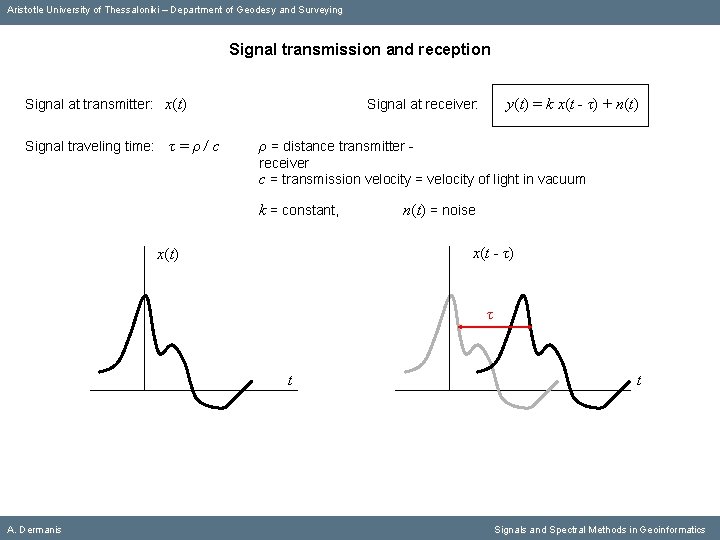
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and reception Signal at transmitter: x(t) Signal at receiver: k = constant, A. Dermanis y(t) = k x(t - τ) + n(t) = noise Signals and Spectral Methods in Geoinformatics

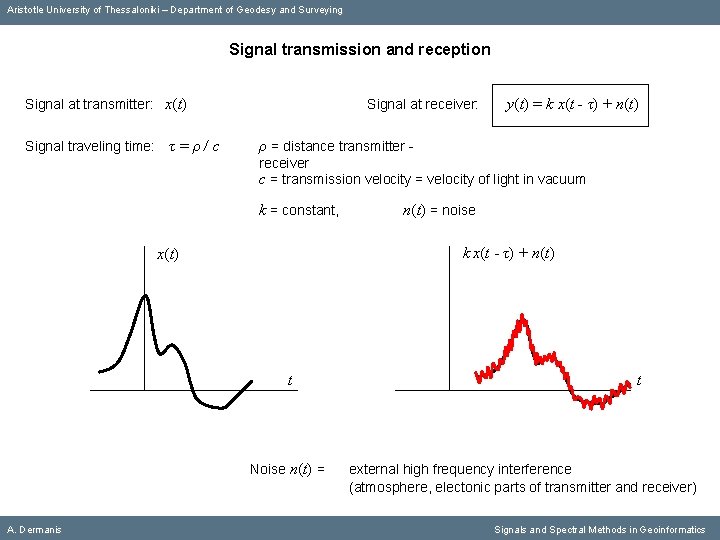
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and reception Signal at transmitter: x(t) Signal traveling time: τ=ρ/c Signal at receiver: y(t) = k x(t - τ) + n(t) ρ = distance transmitter receiver c = transmission velocity = velocity of light in vacuum k = constant, A. Dermanis n(t) = noise Signals and Spectral Methods in Geoinformatics

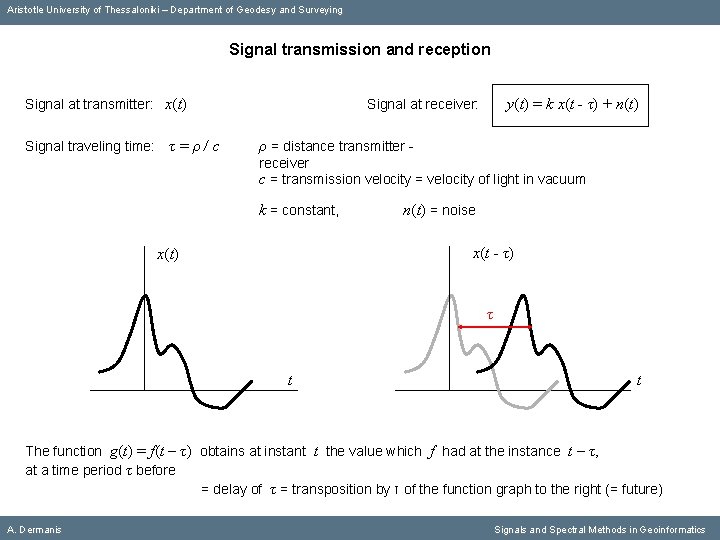
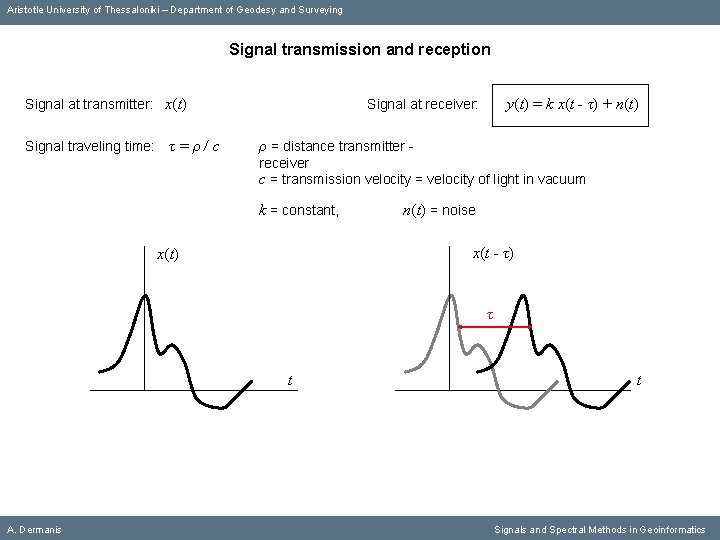
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and reception Signal at transmitter: x(t) Signal traveling time: τ=ρ/c y(t) = k x(t - τ) + n(t) Signal at receiver: ρ = distance transmitter receiver c = transmission velocity = velocity of light in vacuum k = constant, n(t) = noise x(t - τ) x(t) τ t t The function g(t) = f(t – τ) obtains at instant t the value which f had at the instance t – τ, at a time period τ before = delay of τ = transposition by τ of the function graph to the right (= future) A. Dermanis Signals and Spectral Methods in Geoinformatics

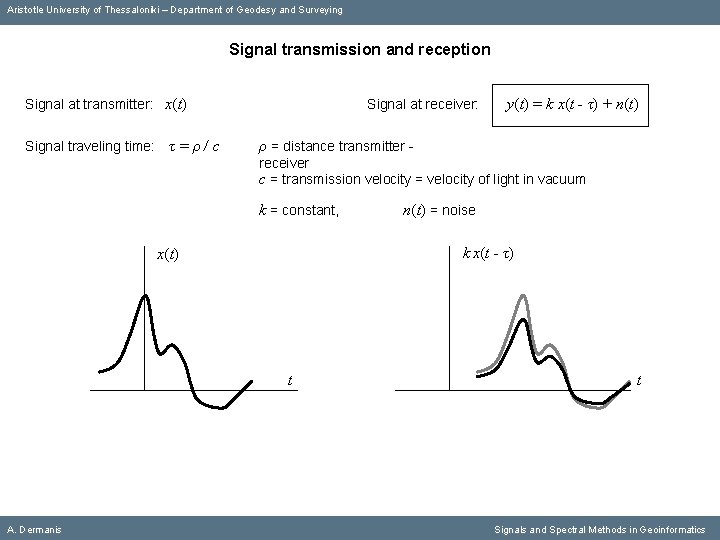
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and reception Signal at transmitter: x(t) Signal traveling time: τ=ρ/c Signal at receiver: y(t) = k x(t - τ) + n(t) ρ = distance transmitter receiver c = transmission velocity = velocity of light in vacuum k = constant, k x(t - τ) x(t) t A. Dermanis n(t) = noise t Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal transmission and reception Signal at transmitter: x(t) Signal traveling time: τ=ρ/c Signal at receiver: y(t) = k x(t - τ) + n(t) ρ = distance transmitter receiver c = transmission velocity = velocity of light in vacuum k = constant, k x(t - τ) + n(t) x(t) t Noise n(t) = A. Dermanis n(t) = noise t external high frequency interference (atmosphere, electonic parts of transmitter and receiver) Signals and Spectral Methods in Geoinformatics

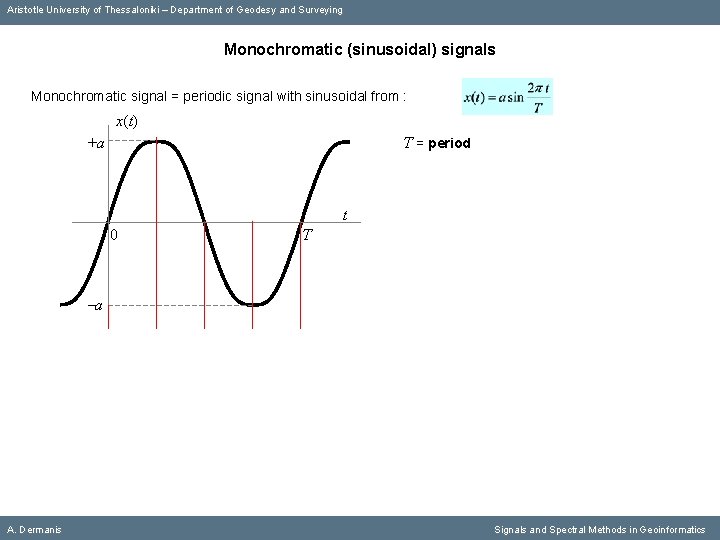
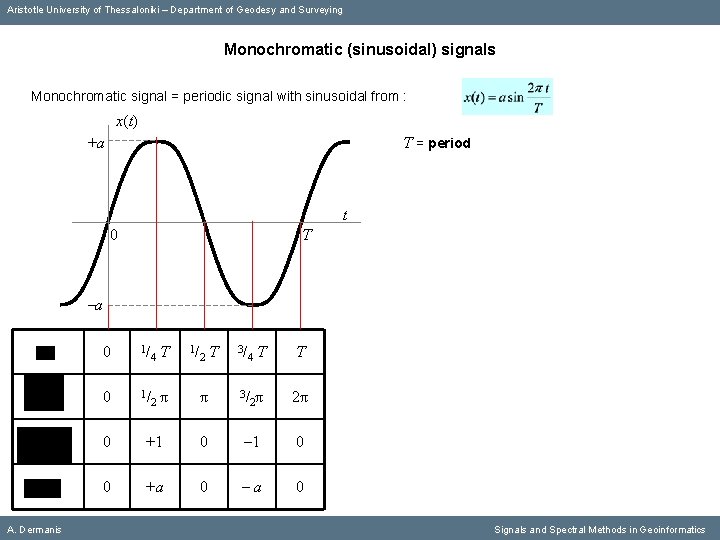
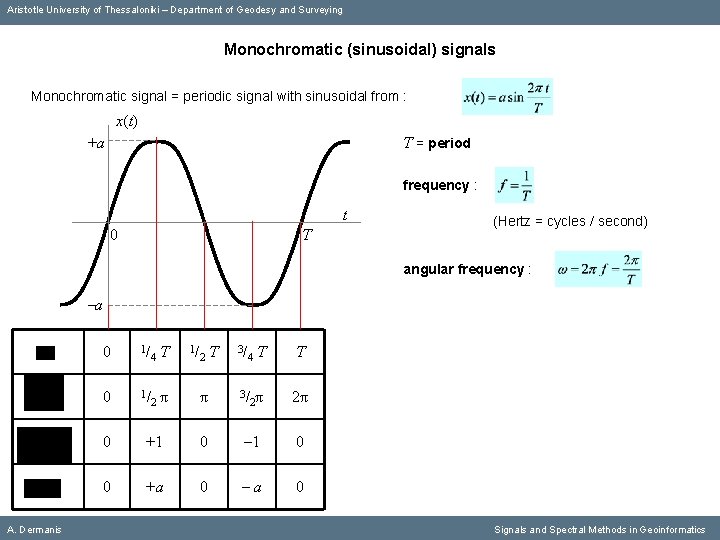
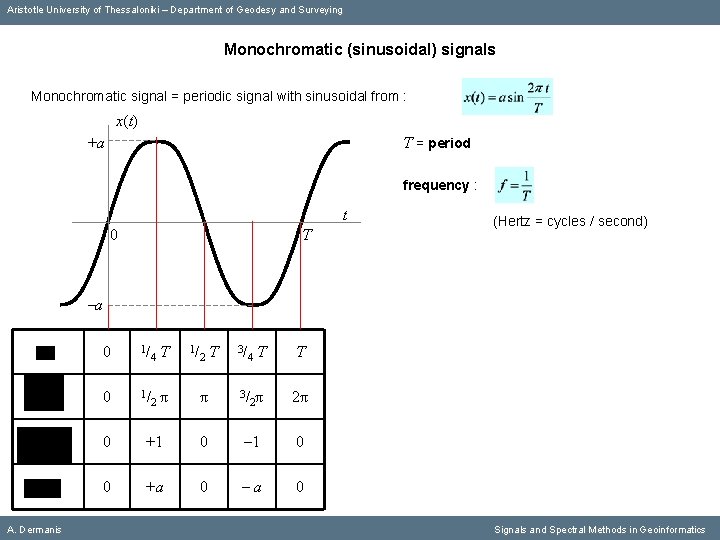
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Monochromatic (sinusoidal) signals Monochromatic signal = periodic signal with sinusoidal from : x(t) +a T = period frequency : t 0 T (Hertz = cycles / second) -a A. Dermanis 0 1/ 4 2 T π 1/ 2 T 3/ 4 π 3/ T 2π 0 +1 0 0 +a 0 Signals and Spectral Methods in Geoinformatics

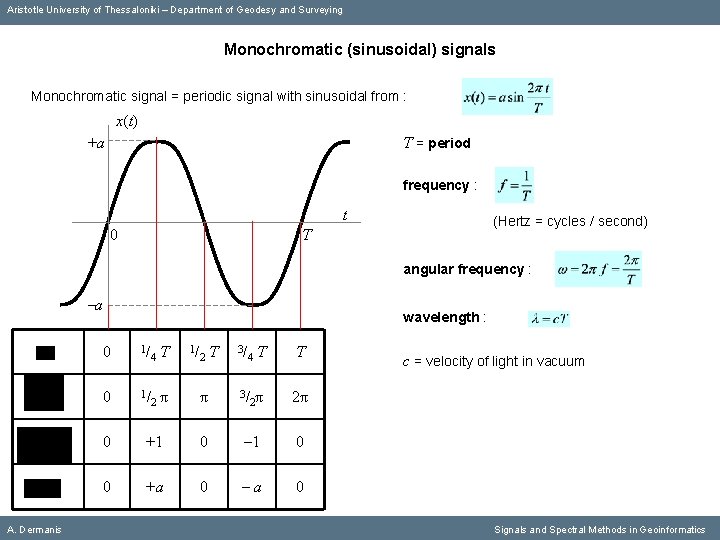
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Monochromatic (sinusoidal) signals Monochromatic signal = periodic signal with sinusoidal from : x(t) +a T = period frequency : t 0 T (Hertz = cycles / second) angular frequency : -a A. Dermanis 0 1/ 4 2 T π 1/ 2 T 3/ 4 π 3/ T 2π 0 +1 0 0 +a 0 Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Monochromatic (sinusoidal) signals Monochromatic signal = periodic signal with sinusoidal from : x(t) +a T = period frequency : t 0 (Hertz = cycles / second) T angular frequency : -a A. Dermanis wavelength : 0 1/ 4 2 T π 1/ 2 T 3/ 4 π 3/ T 2π T c = velocity of light in vacuum 2π 0 +1 0 0 +a 0 Signals and Spectral Methods in Geoinformatics

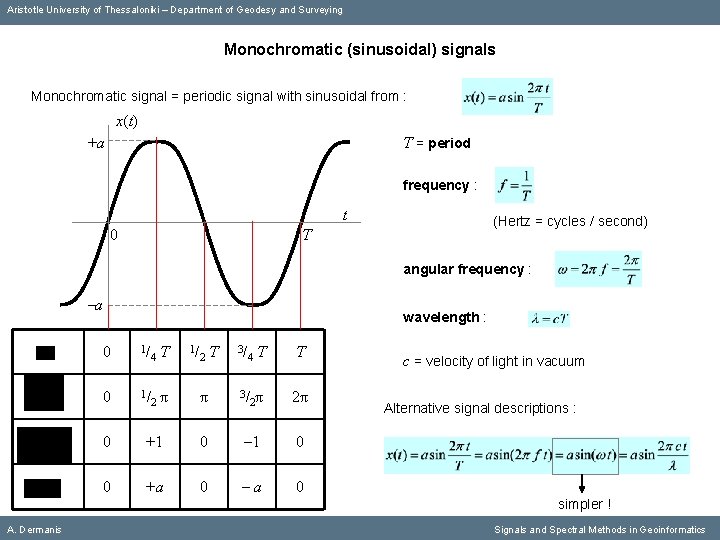
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Monochromatic (sinusoidal) signals Monochromatic signal = periodic signal with sinusoidal from : x(t) +a T = period frequency : t 0 (Hertz = cycles / second) T angular frequency : -a wavelength : 0 1/ 4 2 T π 1/ 2 T 3/ 4 π 3/ T 2π 0 +1 0 0 +a 0 c = velocity of light in vacuum Alternative signal descriptions : simpler ! A. Dermanis Signals and Spectral Methods in Geoinformatics

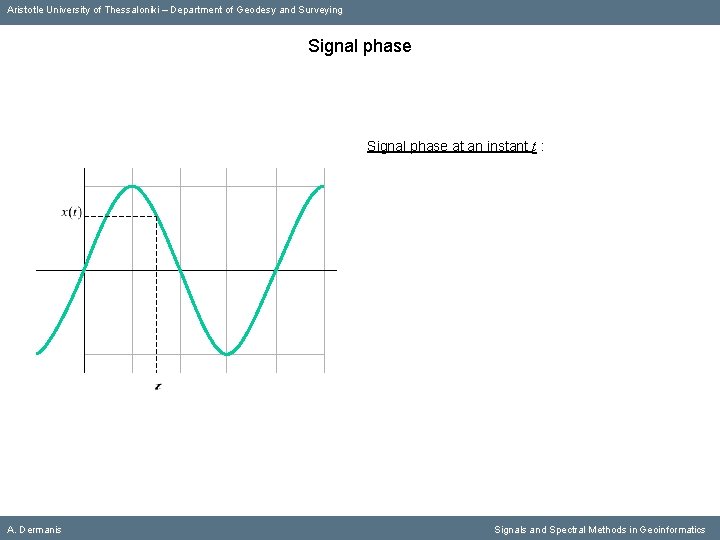
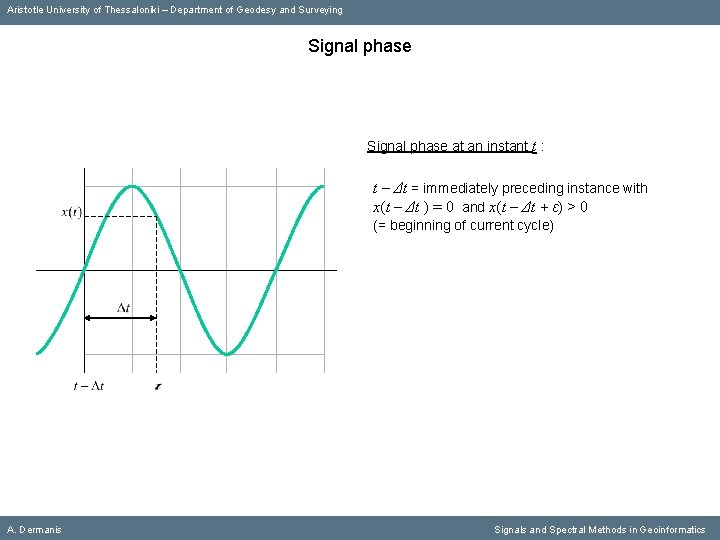
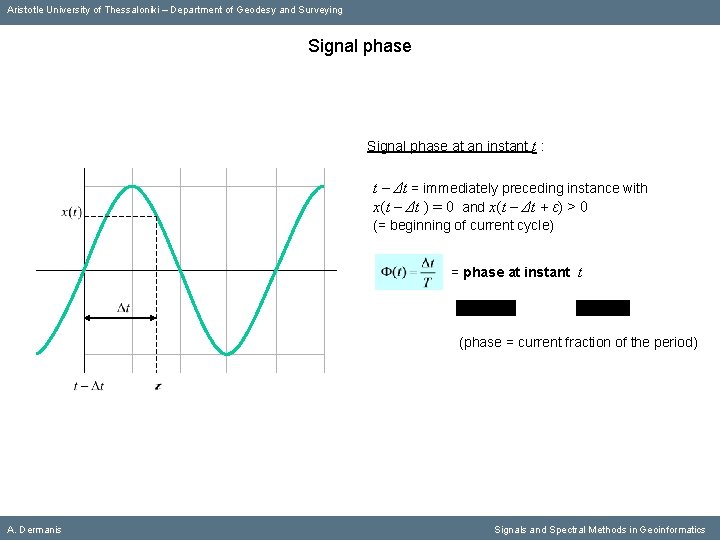
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase at an instant t : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase at an instant t : t – Δt = immediately preceding instance with x(t – Δt ) = 0 and x(t – Δt + ε) > 0 (= beginning of current cycle) A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase at an instant t : t – Δt = immediately preceding instance with x(t – Δt ) = 0 and x(t – Δt + ε) > 0 (= beginning of current cycle) = phase at instant t (phase = current fraction of the period) A. Dermanis Signals and Spectral Methods in Geoinformatics

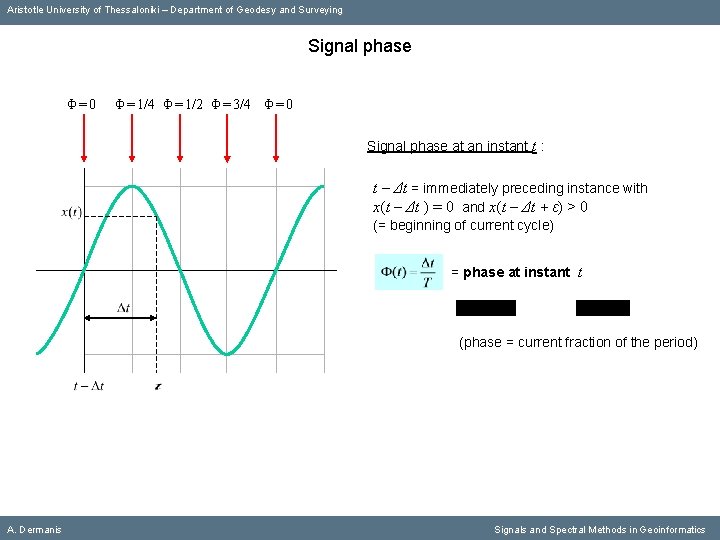
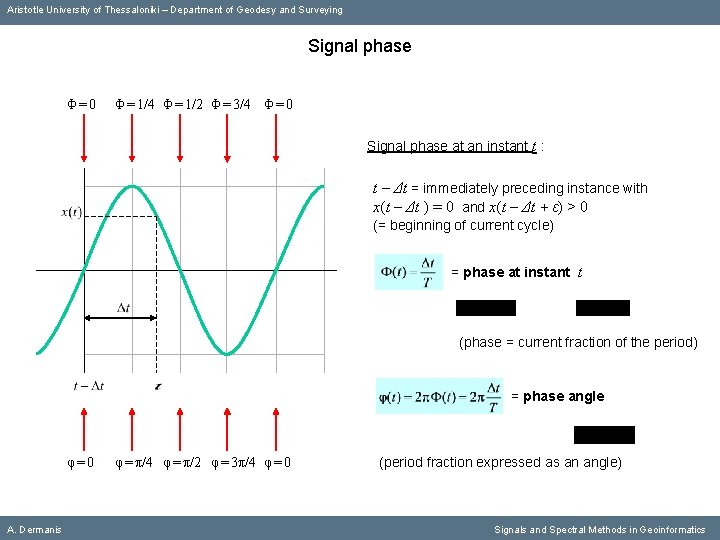
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase Φ=0 Φ = 1/4 Φ = 1/2 Φ = 3/4 Φ = 0 Signal phase at an instant t : t – Δt = immediately preceding instance with x(t – Δt ) = 0 and x(t – Δt + ε) > 0 (= beginning of current cycle) = phase at instant t (phase = current fraction of the period) A. Dermanis Signals and Spectral Methods in Geoinformatics

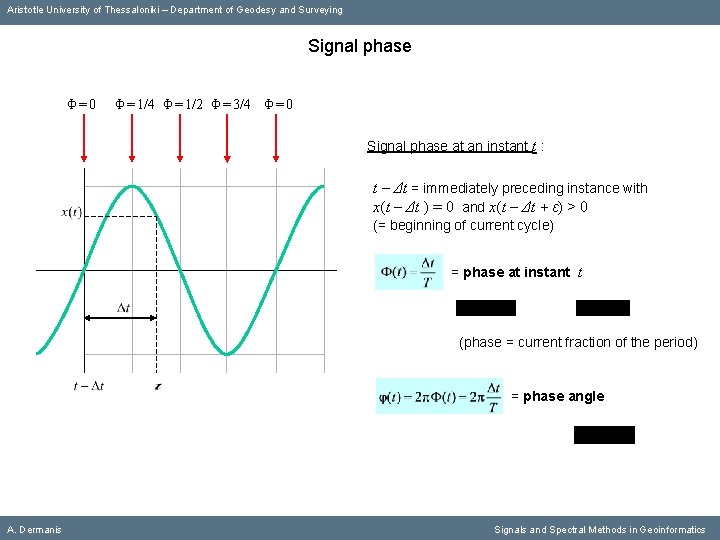
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase Φ=0 Φ = 1/4 Φ = 1/2 Φ = 3/4 Φ = 0 Signal phase at an instant t : t – Δt = immediately preceding instance with x(t – Δt ) = 0 and x(t – Δt + ε) > 0 (= beginning of current cycle) = phase at instant t (phase = current fraction of the period) = phase angle A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Signal phase Φ=0 Φ = 1/4 Φ = 1/2 Φ = 3/4 Φ = 0 Signal phase at an instant t : t – Δt = immediately preceding instance with x(t – Δt ) = 0 and x(t – Δt + ε) > 0 (= beginning of current cycle) = phase at instant t (phase = current fraction of the period) = phase angle φ=0 A. Dermanis φ = π/4 φ = π/2 φ = 3π/4 φ = 0 (period fraction expressed as an angle) Signals and Spectral Methods in Geoinformatics

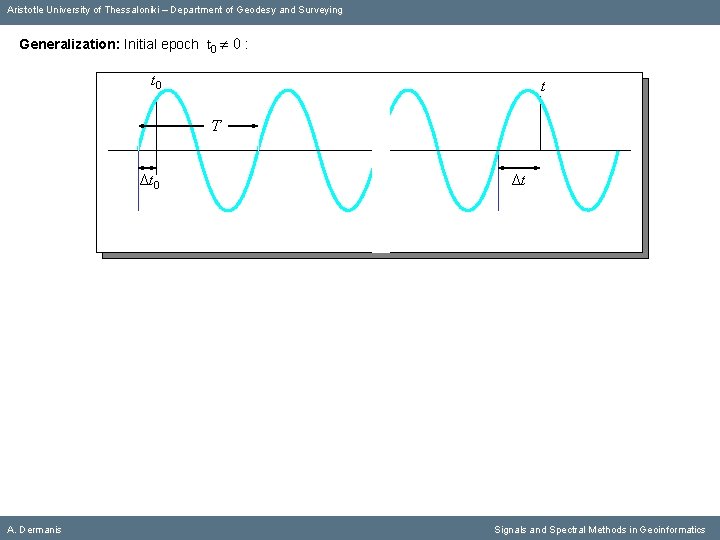
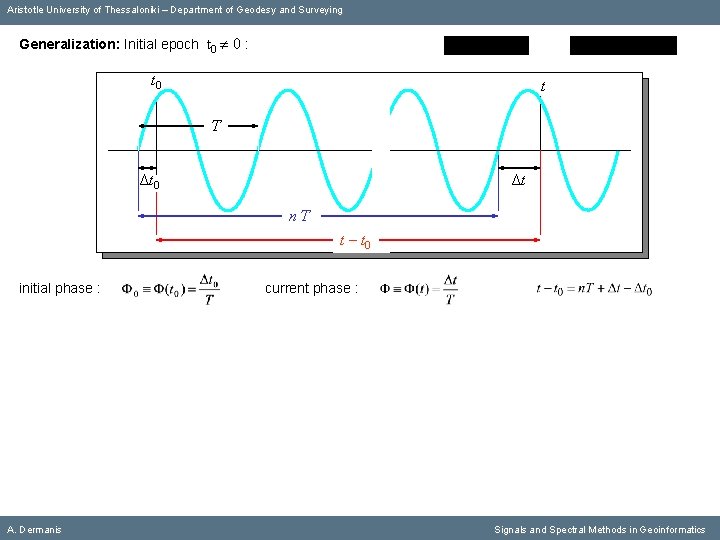
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t 0 0 : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t 0 0 : t 0 t Τ Δt 0 A. Dermanis Δt Signals and Spectral Methods in Geoinformatics

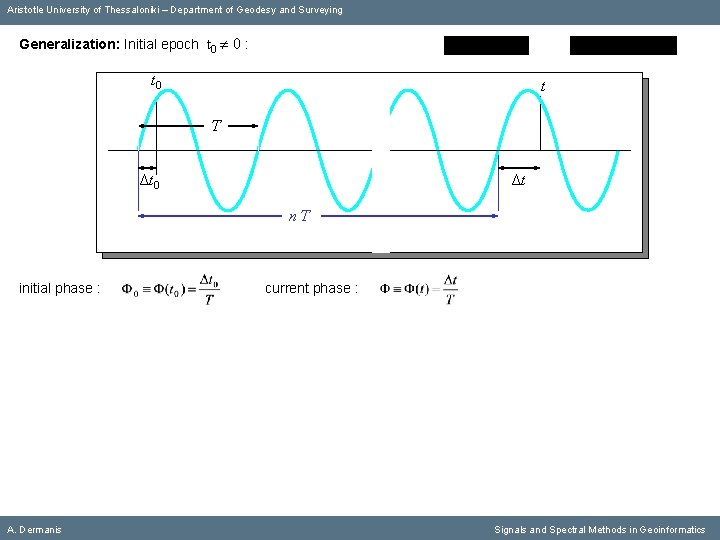
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t 0 0 : t 0 t Τ Δt 0 Δt nΤ initial phase : A. Dermanis current phase : Signals and Spectral Methods in Geoinformatics

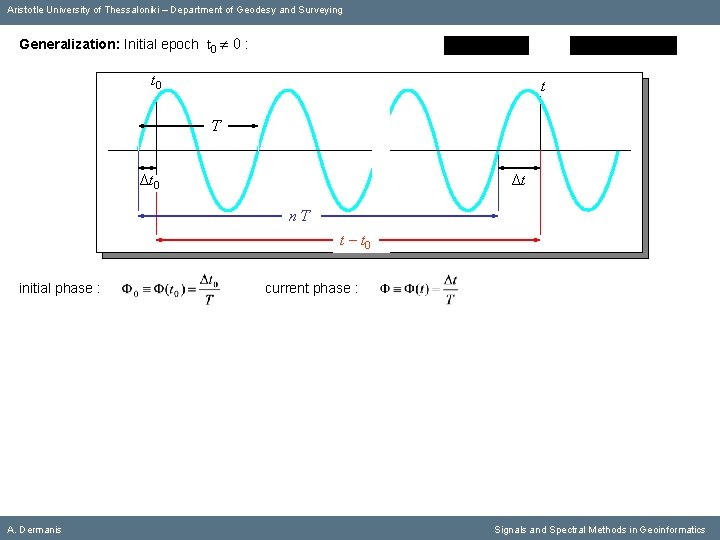
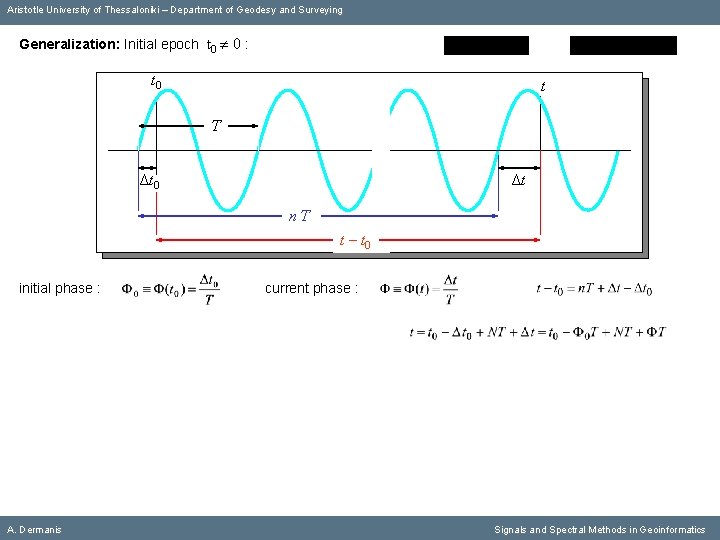
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t 0 0 : t 0 t Τ Δt 0 Δt nΤ t – t 0 initial phase : A. Dermanis current phase : Signals and Spectral Methods in Geoinformatics

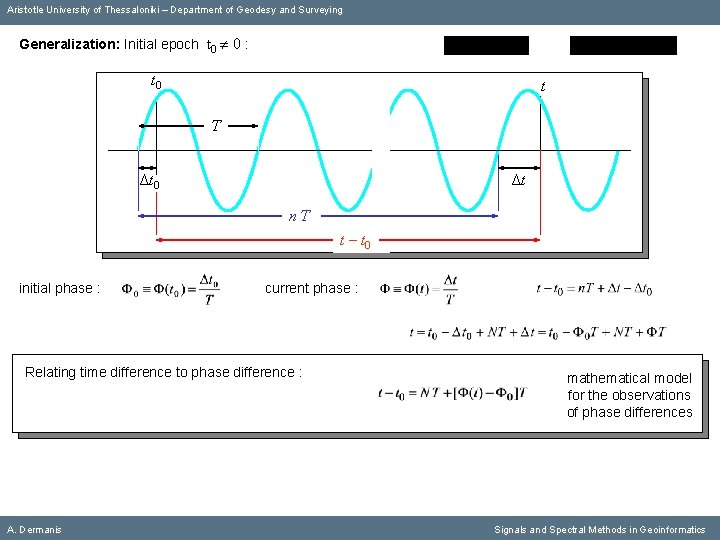
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t 0 0 : t 0 t Τ Δt 0 Δt nΤ t – t 0 initial phase : current phase : Relating time difference to phase difference : A. Dermanis mathematical model for the observations of phase differences Signals and Spectral Methods in Geoinformatics

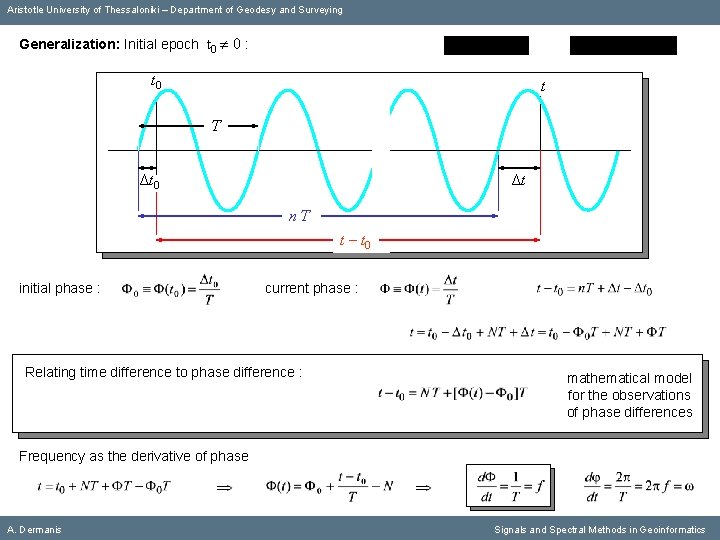
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Generalization: Initial epoch t 0 0 : t 0 t Τ Δt 0 Δt nΤ t – t 0 initial phase : current phase : Relating time difference to phase difference : mathematical model for the observations of phase differences Frequency as the derivative of phase A. Dermanis Signals and Spectral Methods in Geoinformatics

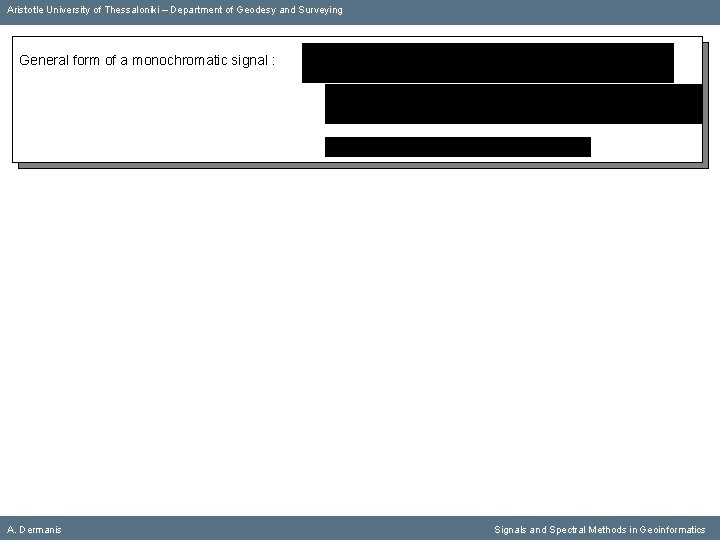
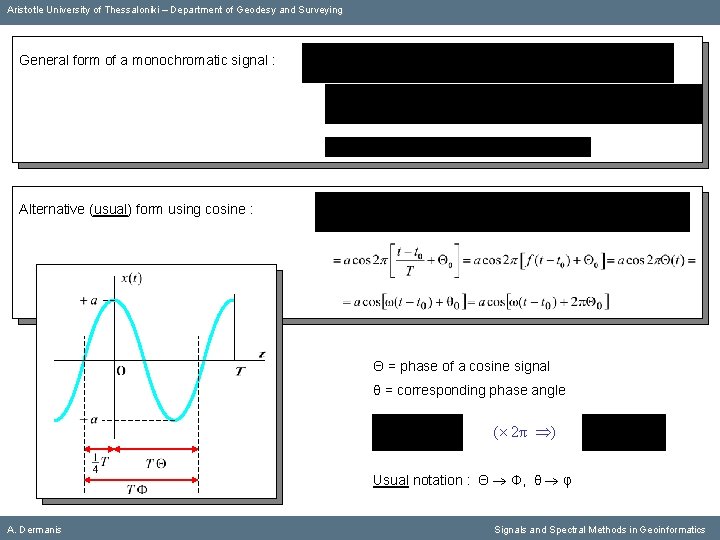
Aristotle University of Thessaloniki – Department of Geodesy and Surveying General form of a monochromatic signal : A. Dermanis Signals and Spectral Methods in Geoinformatics

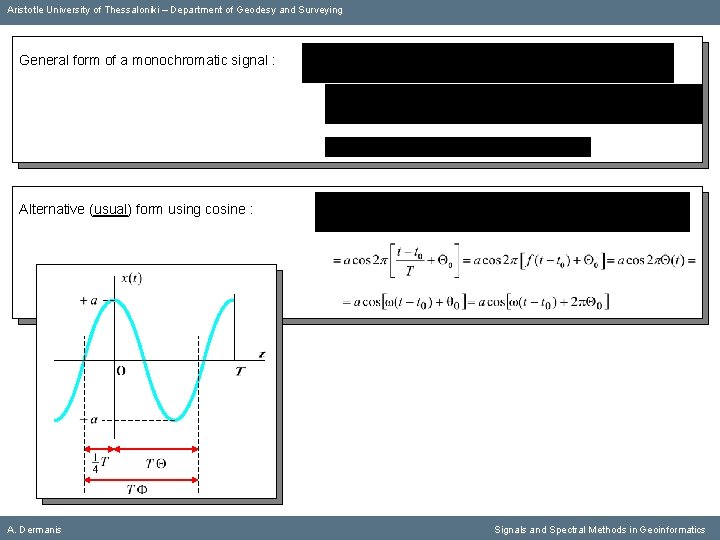
Aristotle University of Thessaloniki – Department of Geodesy and Surveying General form of a monochromatic signal : Alternative (usual) form using cosine : A. Dermanis Signals and Spectral Methods in Geoinformatics

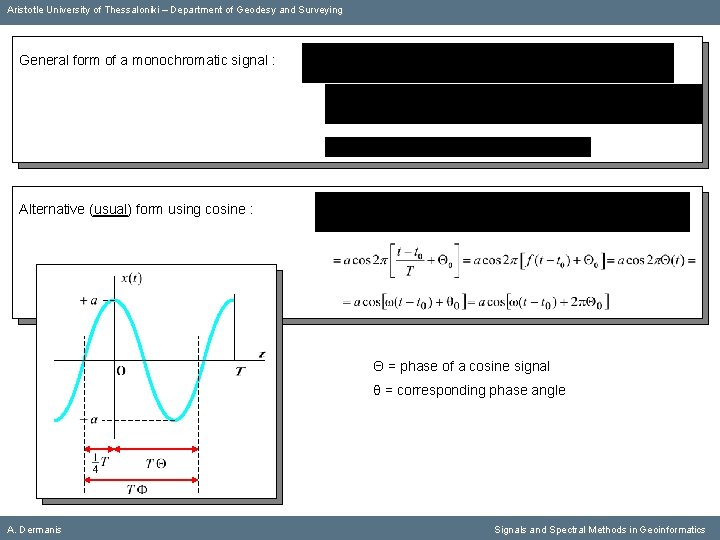
Aristotle University of Thessaloniki – Department of Geodesy and Surveying General form of a monochromatic signal : Alternative (usual) form using cosine : Θ = phase of a cosine signal θ = corresponding phase angle A. Dermanis Signals and Spectral Methods in Geoinformatics

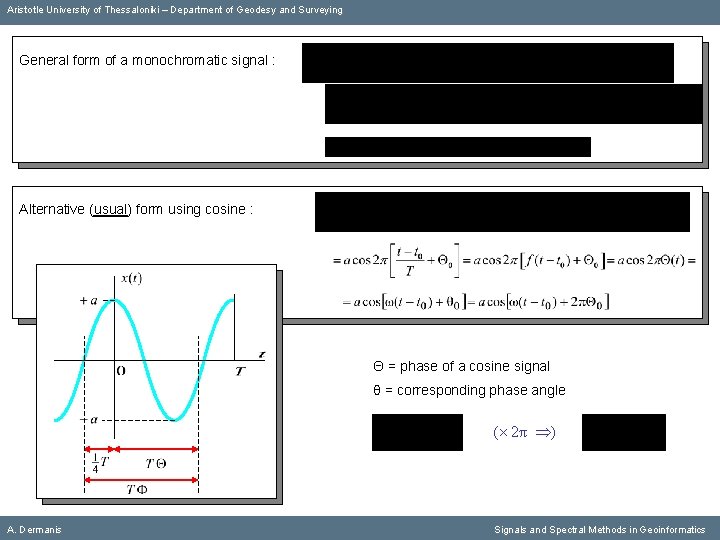
Aristotle University of Thessaloniki – Department of Geodesy and Surveying General form of a monochromatic signal : Alternative (usual) form using cosine : Θ = phase of a cosine signal θ = corresponding phase angle ( 2π ) A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying General form of a monochromatic signal : Alternative (usual) form using cosine : Θ = phase of a cosine signal θ = corresponding phase angle ( 2π ) Usual notation : Θ Φ, θ φ A. Dermanis Signals and Spectral Methods in Geoinformatics

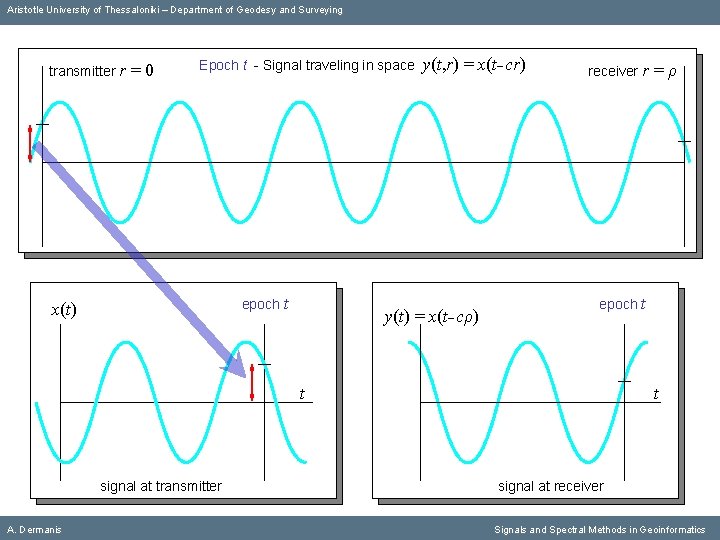
Aristotle University of Thessaloniki – Department of Geodesy and Surveying transmitter r A. Dermanis =0 Epoch t - Signal traveling in space y(t, r) = x(t cr) receiver r =ρ Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying transmitter r =0 Epoch t - Signal traveling in space y(t, r) = x(t cr) receiver r =ρ epoch t x(t) t signal at transmitter A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying transmitter r =0 Epoch t - Signal traveling in space epoch t x(t) y(t, r) = x(t cr) y(t) = x(t cρ) receiver r epoch t t signal at transmitter A. Dermanis =ρ t signal at receiver Signals and Spectral Methods in Geoinformatics

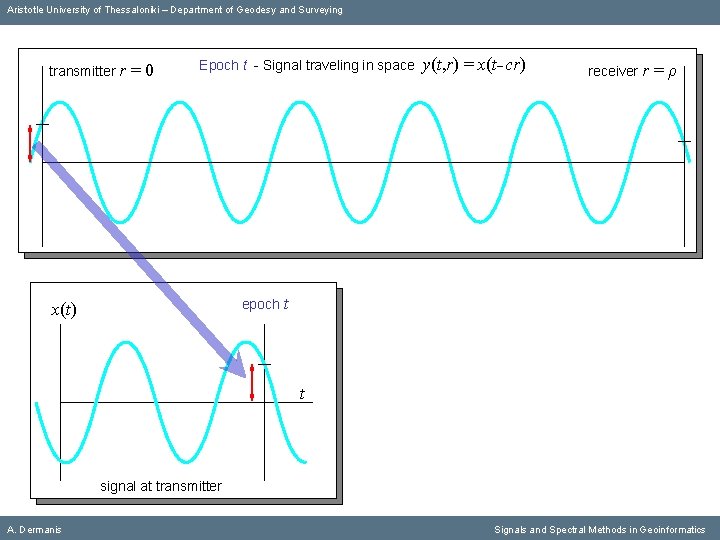
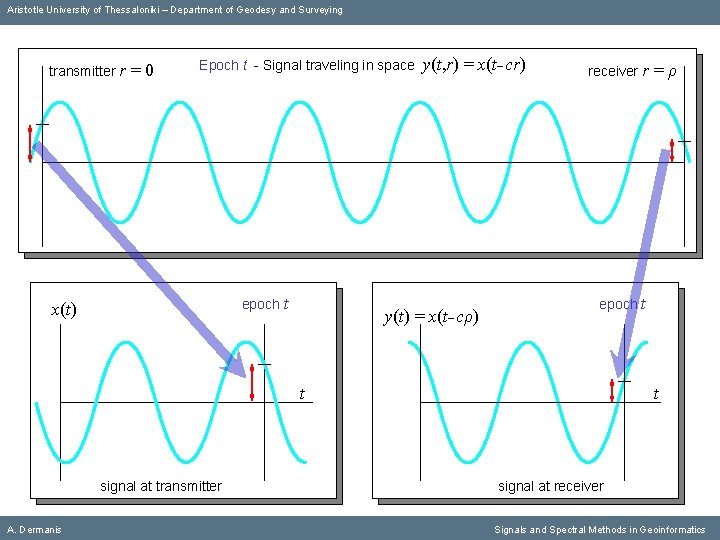
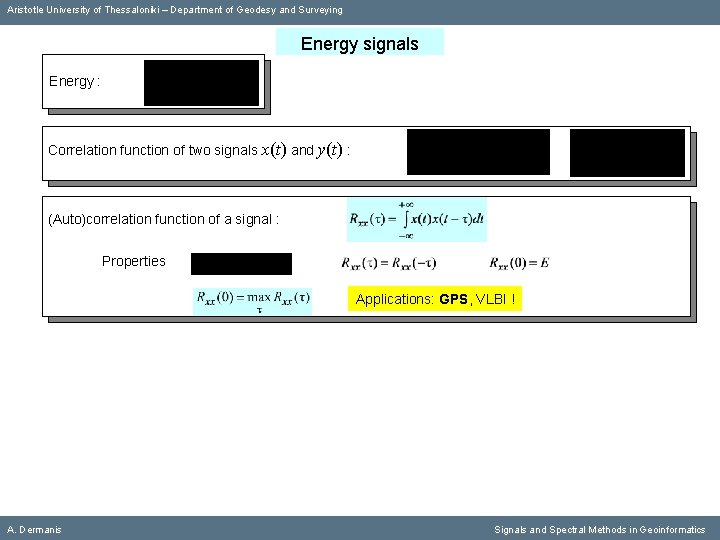
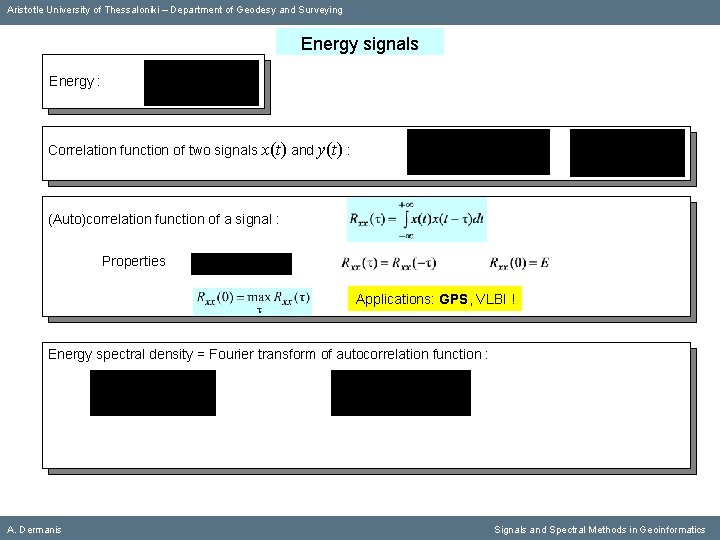
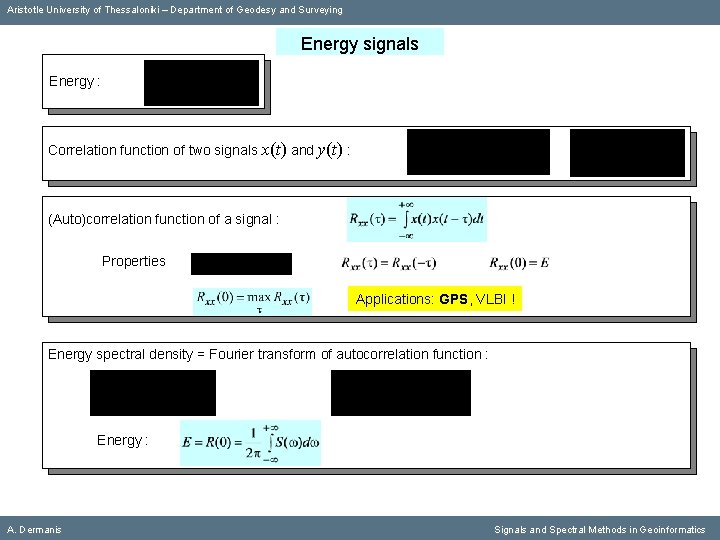
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy : Correlation function of two signals x(t) and y(t) : A. Dermanis Signals and Spectral Methods in Geoinformatics

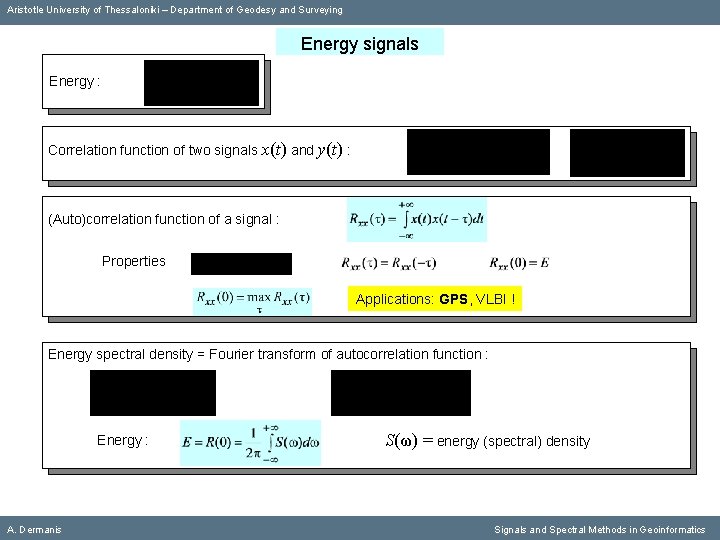
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy : Correlation function of two signals x(t) and y(t) : (Auto)correlation function of a signal : Properties Applications: GPS, VLBI ! Energy spectral density = Fourier transform of autocorrelation function : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy : Correlation function of two signals x(t) and y(t) : (Auto)correlation function of a signal : Properties Applications: GPS, VLBI ! Energy spectral density = Fourier transform of autocorrelation function : Energy : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy : Correlation function of two signals x(t) and y(t) : (Auto)correlation function of a signal : Properties Applications: GPS, VLBI ! Energy spectral density = Fourier transform of autocorrelation function : Energy : A. Dermanis S(ω) = energy (spectral) density Signals and Spectral Methods in Geoinformatics

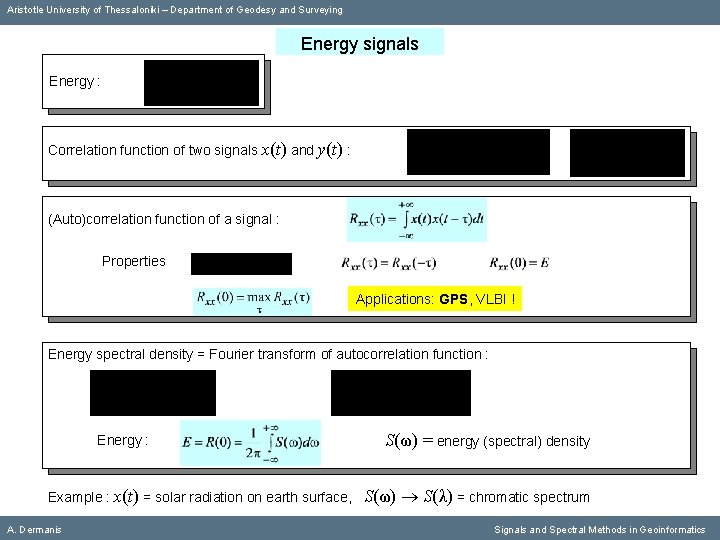
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy signals Energy : Correlation function of two signals x(t) and y(t) : (Auto)correlation function of a signal : Properties Applications: GPS, VLBI ! Energy spectral density = Fourier transform of autocorrelation function : Energy : Example : x(t) = solar radiation on earth surface, A. Dermanis S(ω) = energy (spectral) density S(ω) S(λ) = chromatic spectrum Signals and Spectral Methods in Geoinformatics

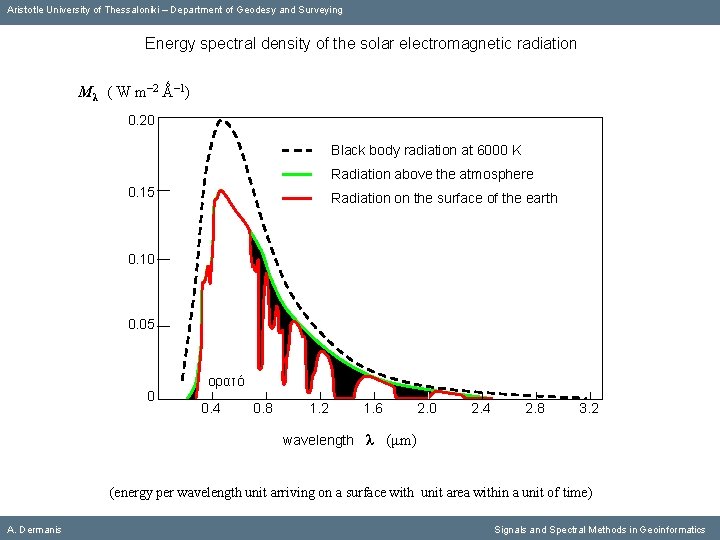
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Energy spectral density of the solar electromagnetic radiation Μλ ( W m 2 Ǻ 1) 0. 20 Black body radiation at 6000 Κ Radiation above the atmosphere 0. 15 Radiation on the surface of the earth 0. 10 0. 05 0 ορατό 0. 4 0. 8 1. 2 1. 6 2. 0 2. 4 2. 8 3. 2 wavelength λ (μm) (energy per wavelength unit arriving on a surface with unit area within a unit of time) A. Dermanis Signals and Spectral Methods in Geoinformatics

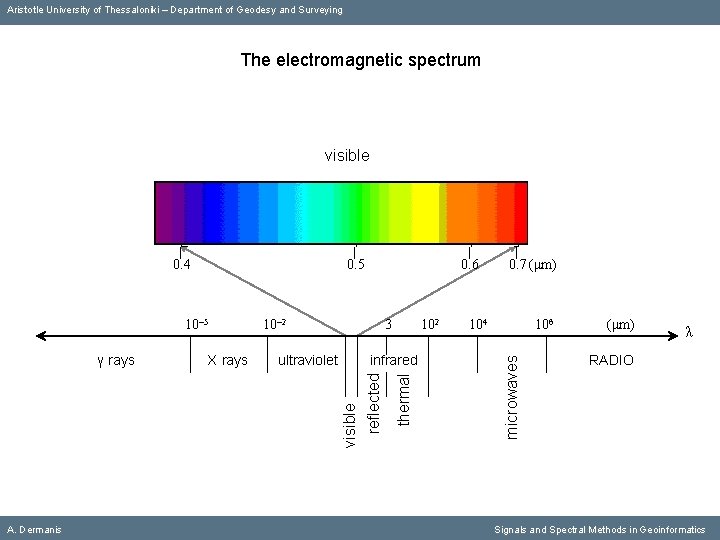
Aristotle University of Thessaloniki – Department of Geodesy and Surveying The electromagnetic spectrum visible 10 5 Χ rays 10 2 ultraviolet 3 A. Dermanis 102 infrared visible reflected γ rays 0. 6 0. 7 (μm) 104 106 microwaves 0. 5 thermal 0. 4 (μm) λ RADIO Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : A. Dermanis power for the interval [–Τ /2, Τ /2] Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : power for the interval [–Τ /2, Τ /2] power for the interval [– , + ] A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Power of a periodic signal with period Τ Power for one period Τ : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Power of a periodic signal with period Τ Power for one period Τ : Total power for the interval [– , + ] : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Power of a periodic signal with period Τ Power for one period Τ : (n 1)T Total power for the interval [– , + ] : A. Dermanis (n 1)T Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Power of a periodic signal with period Τ Power for one period Τ : (n 1)T Total power for the interval [– , + ] : (n 1)T The power P of a periodic signal is equal to the power PT for only one period P = PT A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Correlation function of two signals x(t) and y(t) : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Correlation function of two signals x(t) and y(t) : (auto)correlation function of a signal : Properties Εφαρνογές GPS, VLBI ! A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Correlation function of two signals x(t) and y(t) : (auto)correlation function of a signal : Properties Εφαρνογές GPS, VLBI ! Power spectral density = Fourier transform of the autocorrelation function : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Power signals Power : Correlation function of two signals x(t) and y(t) : (auto)correlation function of a signal : Properties Εφαρνογές GPS, VLBI ! Power spectral density = Fourier transform of the autocorrelation function : _ ισχύς : A. Dermanis S(ω) = power (spectral) density Signals and Spectral Methods in Geoinformatics

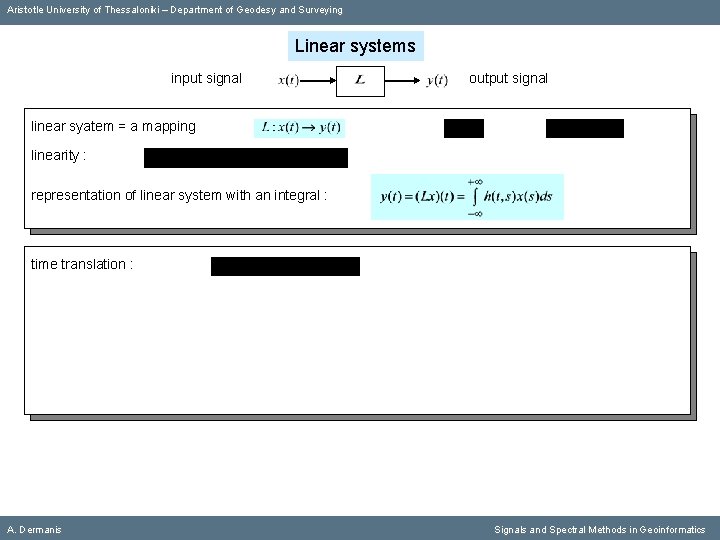
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal A. Dermanis output signal Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal output signal linear syatem = a mapping A. Dermanis Signals and Spectral Methods in Geoinformatics

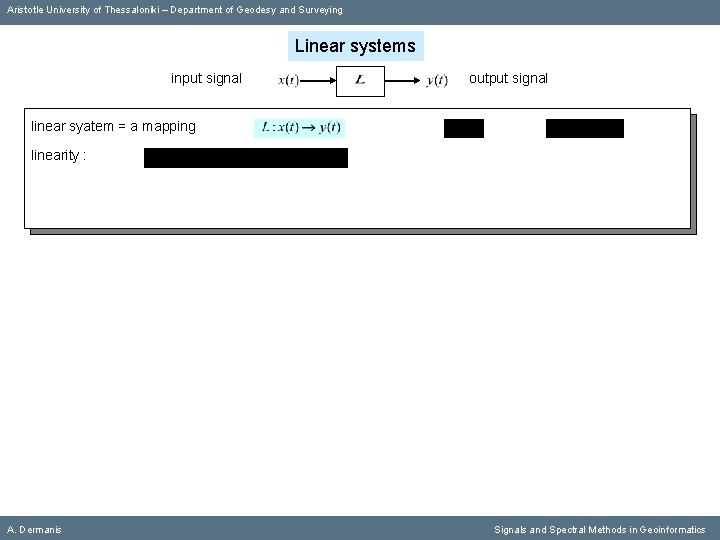
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal output signal linear syatem = a mapping linearity : A. Dermanis Signals and Spectral Methods in Geoinformatics

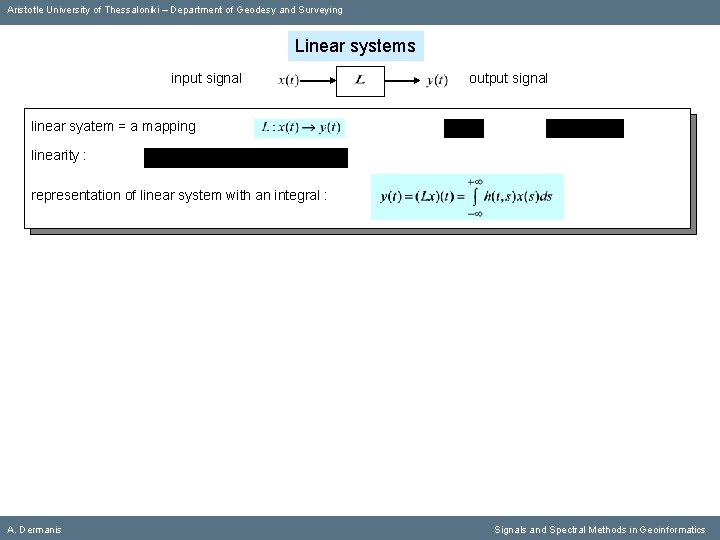
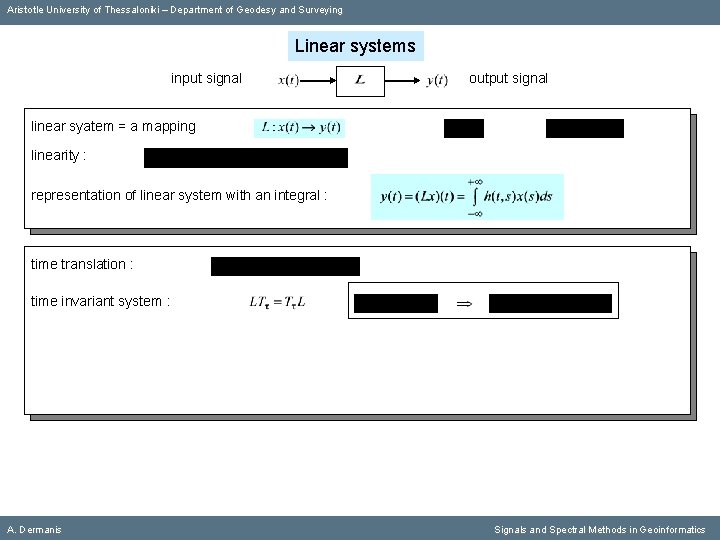
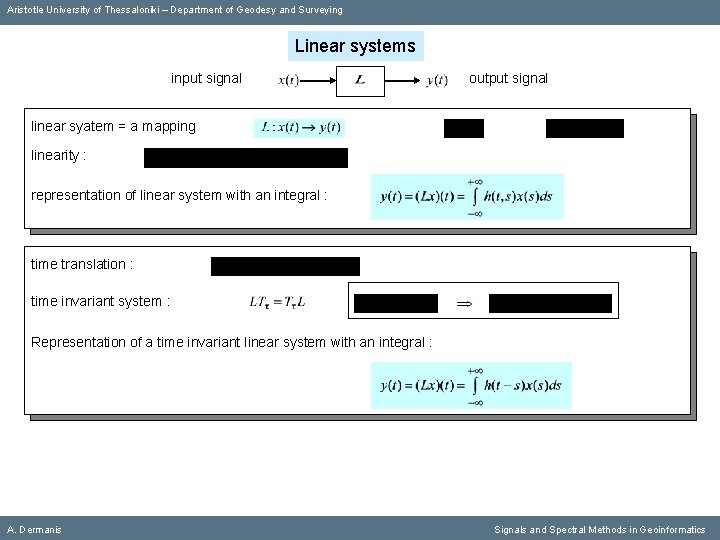
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal output signal linear syatem = a mapping linearity : representation of linear system with an integral : time translation : time invariant system : Representation of a time invariant linear system with an integral : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal output signal linear syatem = a mapping linearity : representation of linear system with an integral : time translation : time invariant system : Representation of a time invariant linear system with an integral : convolution of two functions g(t) and f(t) : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems input signal output signal linear syatem = a mapping linearity : representation of linear system with an integral : time translation : time invariant system : Representation of a time invariant linear system with an integral : convolution of two functions g(t) and f(t) : A. Dermanis time invariant linear system : Signals and Spectral Methods in Geoinformatics

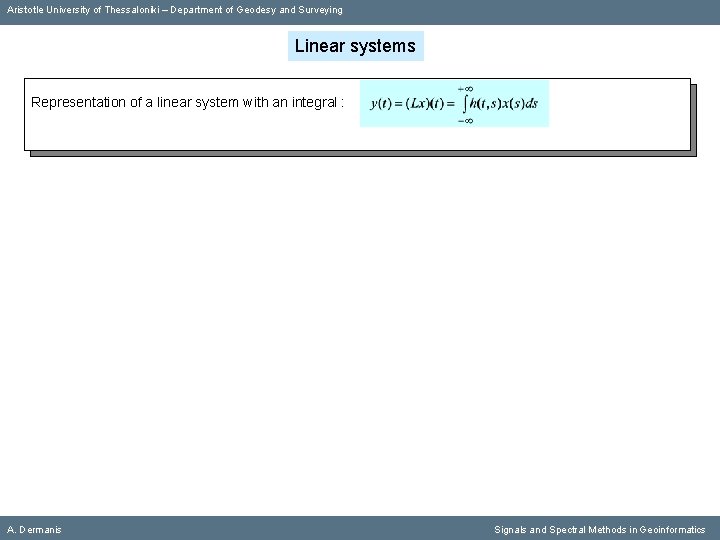
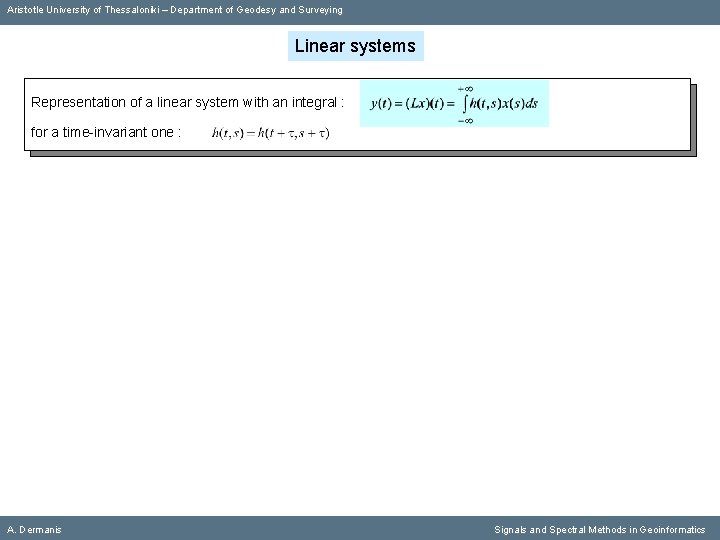
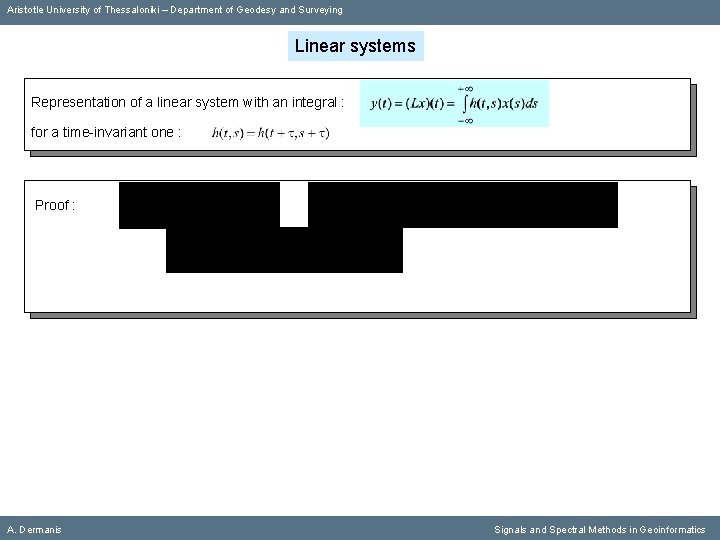
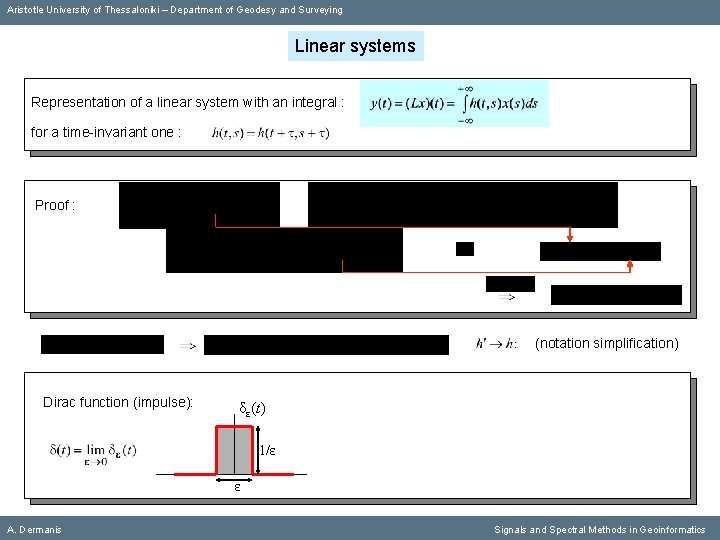
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : A. Dermanis Signals and Spectral Methods in Geoinformatics

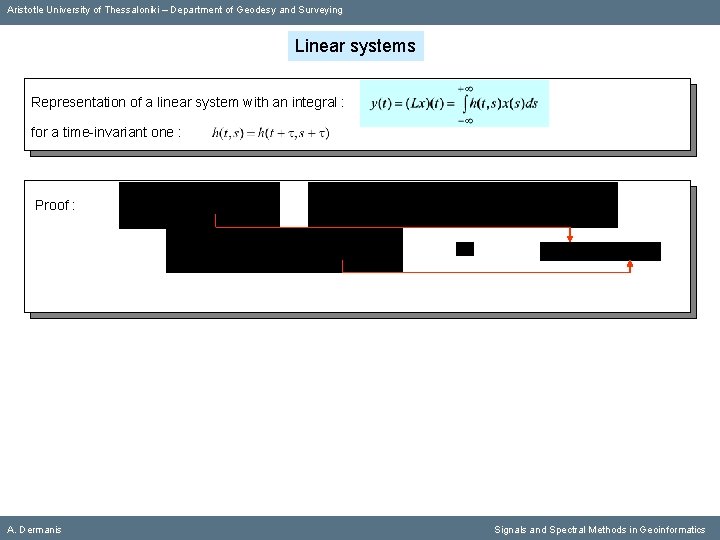
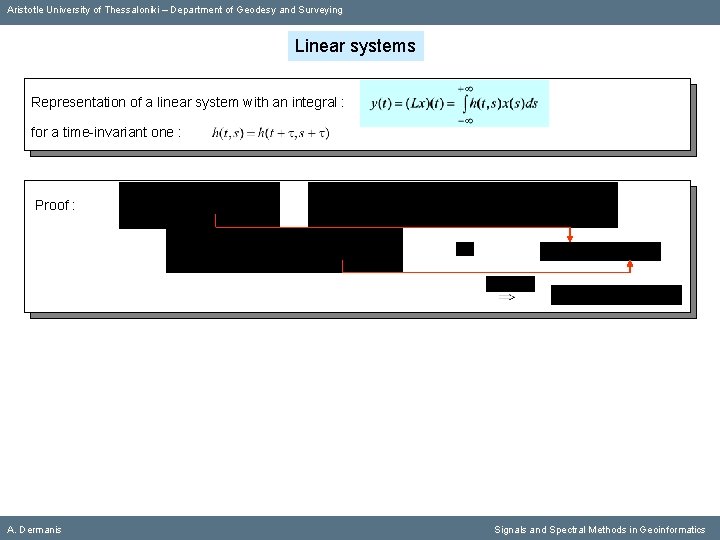
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : Proof : A. Dermanis Signals and Spectral Methods in Geoinformatics

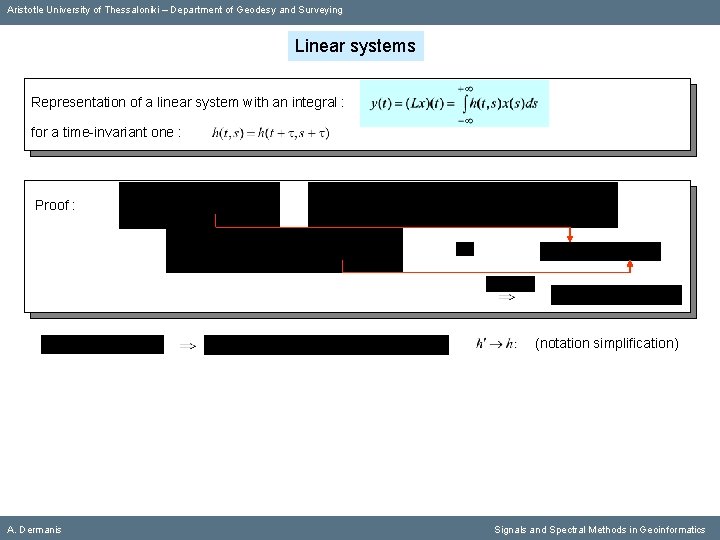
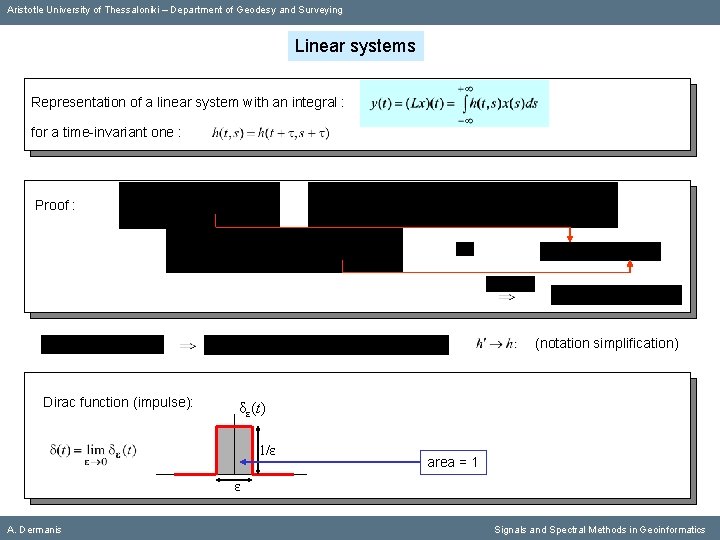
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : Proof : (notation simplification) A. Dermanis Signals and Spectral Methods in Geoinformatics

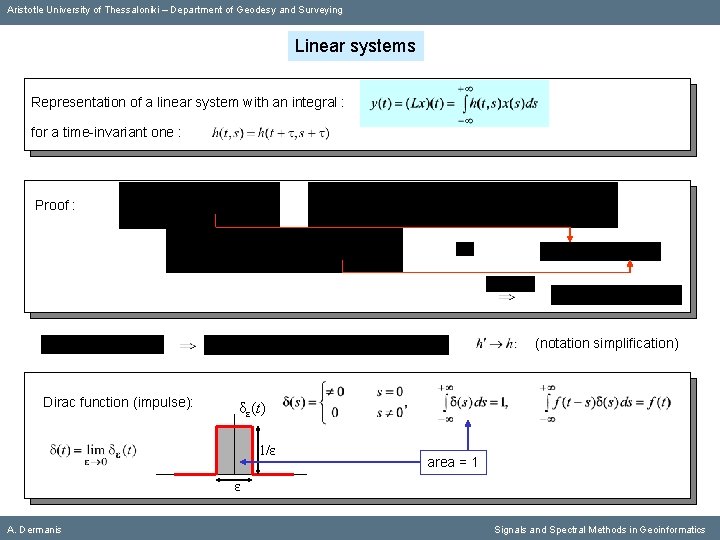
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : Proof : (notation simplification) Dirac function (impulse): δε(t) 1/ε ε A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : Proof : (notation simplification) Dirac function (impulse): δε(t) 1/ε area = 1 ε A. Dermanis Signals and Spectral Methods in Geoinformatics

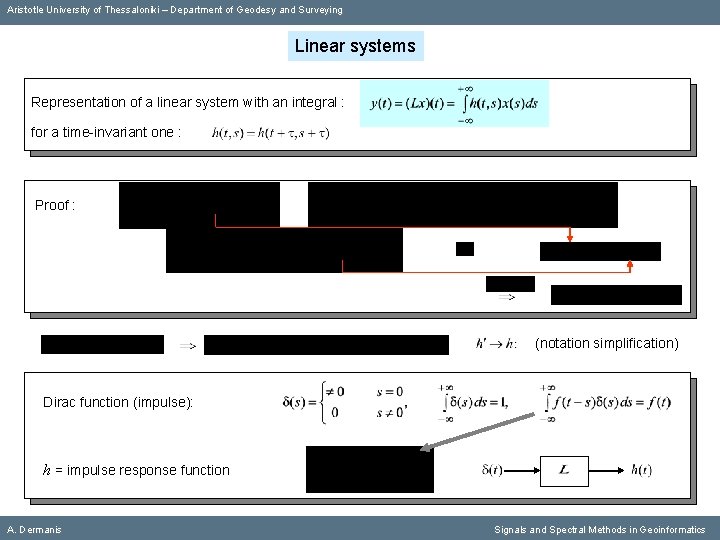
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : Proof : (notation simplification) Dirac function (impulse): A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Linear systems Representation of a linear system with an integral : for a time-invariant one : Proof : (notation simplification) Dirac function (impulse): h = impulse response function A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem A. Dermanis Signals and Spectral Methods in Geoinformatics

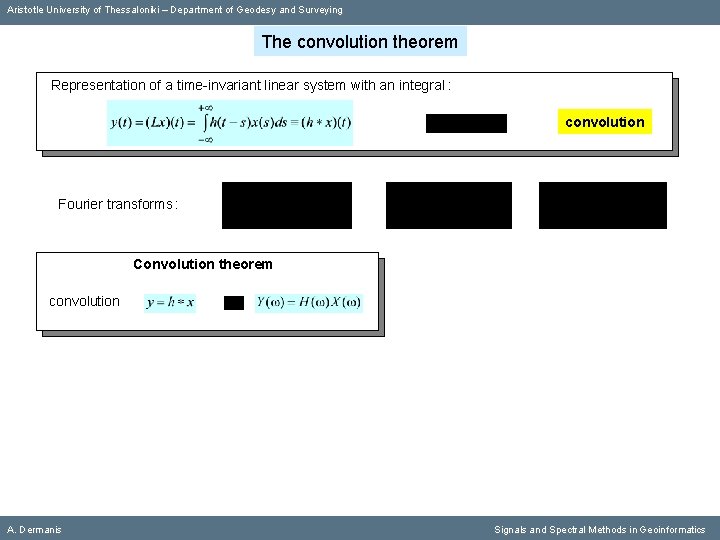
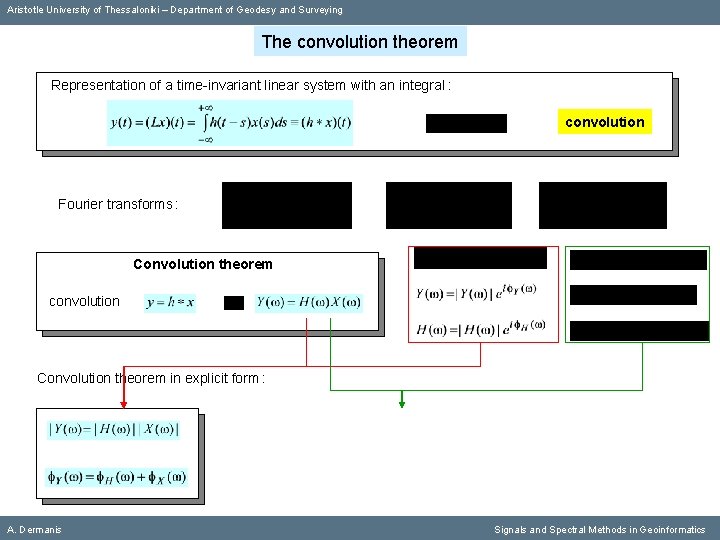
Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem Representation of a time-invariant linear system with an integral : convolution A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem Representation of a time-invariant linear system with an integral : convolution Fourier transforms : A. Dermanis Signals and Spectral Methods in Geoinformatics

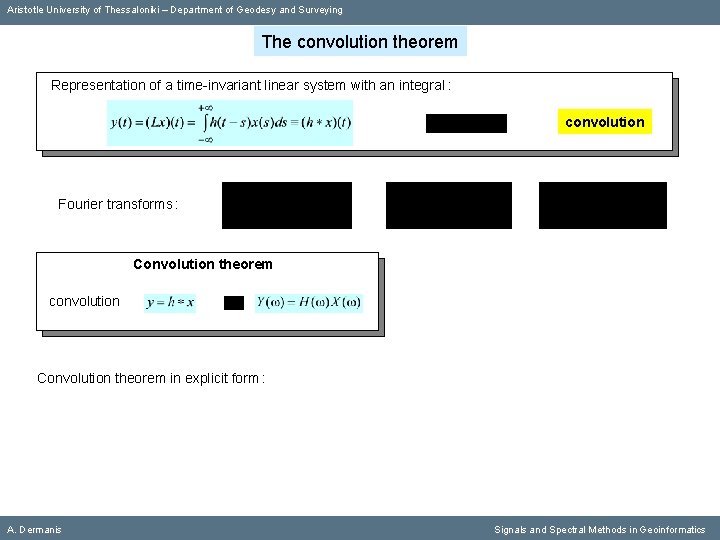
Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem Representation of a time-invariant linear system with an integral : convolution Fourier transforms : Convolution theorem convolution A. Dermanis Signals and Spectral Methods in Geoinformatics

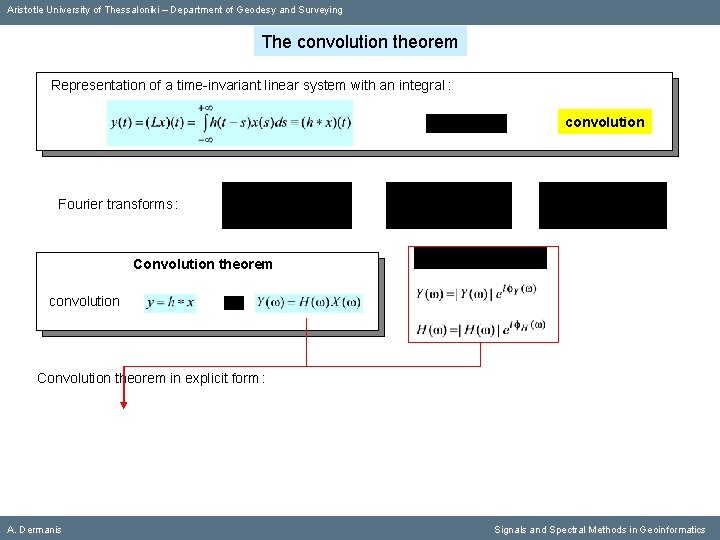
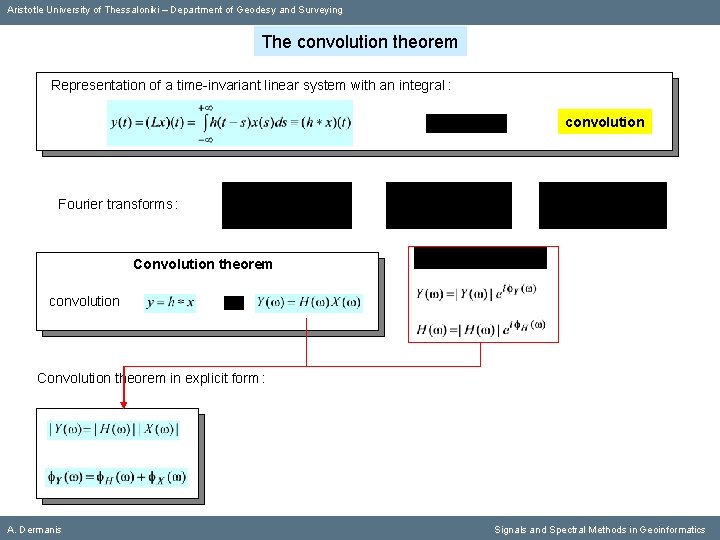
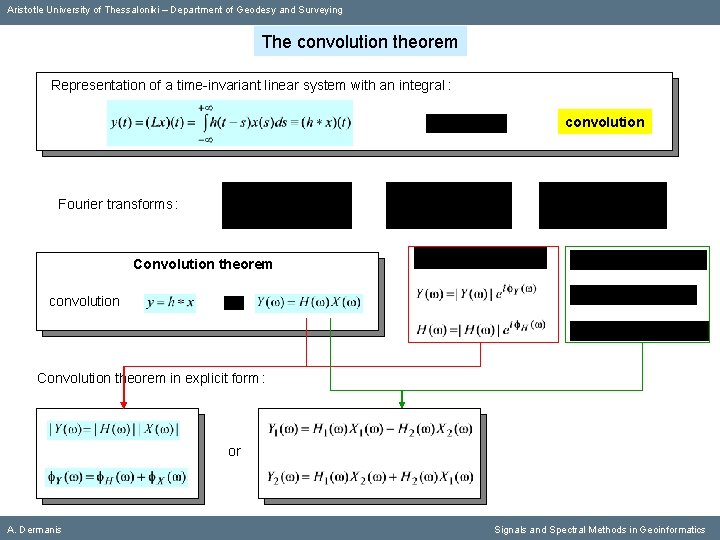
Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem Representation of a time-invariant linear system with an integral : convolution Fourier transforms : Convolution theorem convolution Convolution theorem in explicit form : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying The convolution theorem Representation of a time-invariant linear system with an integral : convolution Fourier transforms : Convolution theorem convolution Convolution theorem in explicit form : or A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Φίλτρα = χρονικά αμετάβλητα γραμμικά συστήματα L A. Dermanis με Η(ω) = 0 σε τμήματα συχνοτήτων ω (= αποκοπή ορισμένων συχνοτήτων) Signals and Spectral Methods in Geoinformatics

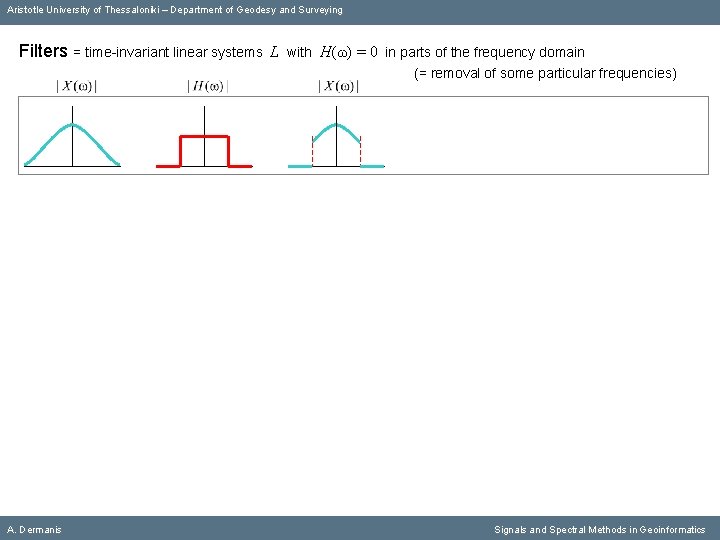
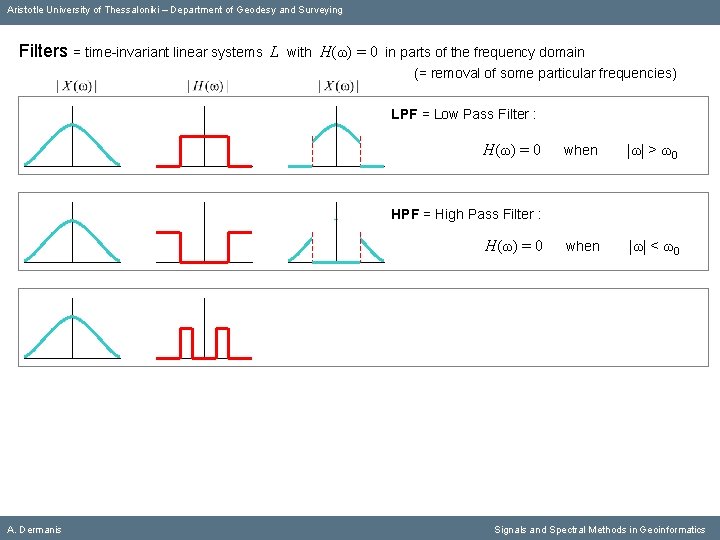
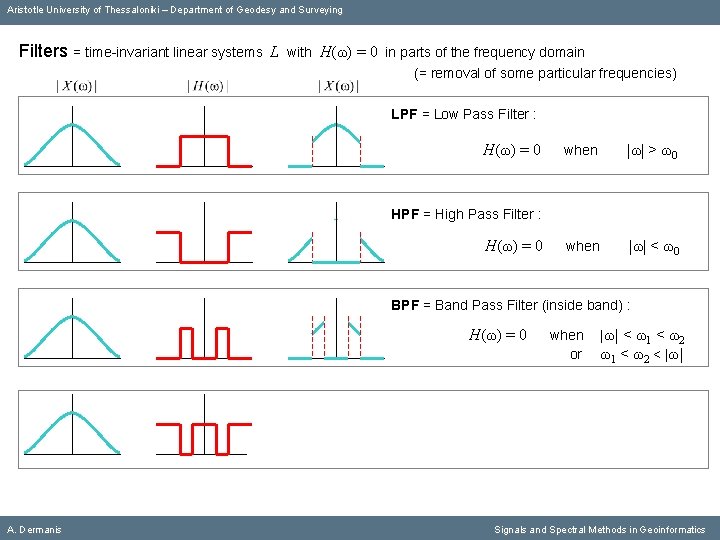
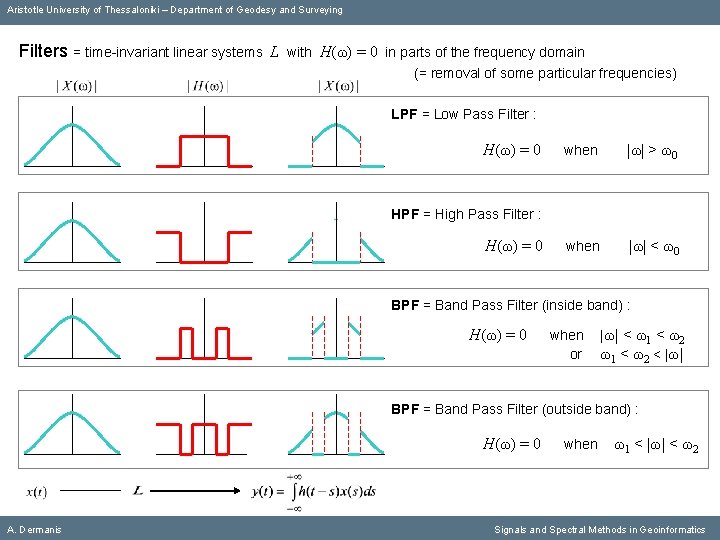
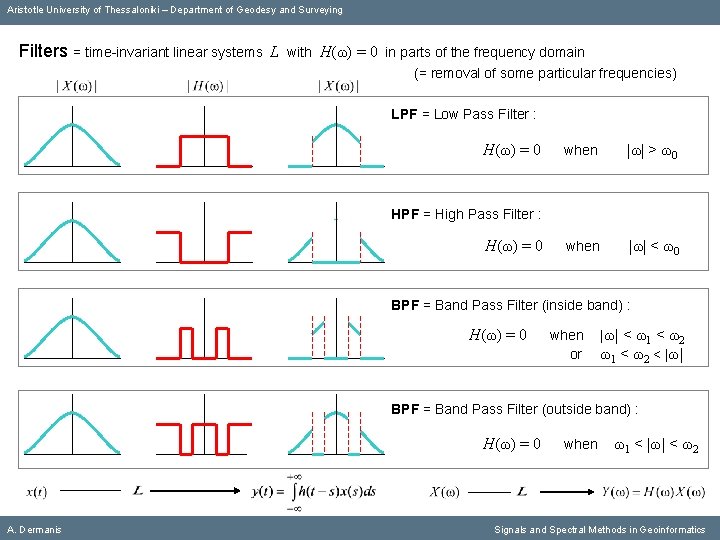
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear systems L A. Dermanis with Η(ω) = 0 in parts of the frequency domain (= removal of some particular frequencies) Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear systems L with Η(ω) = 0 in parts of the frequency domain (= removal of some particular frequencies) LPF = Low Pass Filter : Η(ω) = 0 when |ω| > ω0 when |ω| < ω0 HPF = High Pass Filter : Η(ω) = 0 A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear systems L with Η(ω) = 0 in parts of the frequency domain (= removal of some particular frequencies) LPF = Low Pass Filter : Η(ω) = 0 when |ω| > ω0 when |ω| < ω0 HPF = High Pass Filter : Η(ω) = 0 BPF = Band Pass Filter (inside band) : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear systems L with Η(ω) = 0 in parts of the frequency domain (= removal of some particular frequencies) LPF = Low Pass Filter : Η(ω) = 0 when |ω| > ω0 when |ω| < ω0 HPF = High Pass Filter : Η(ω) = 0 BPF = Band Pass Filter (inside band) : Η(ω) = 0 A. Dermanis when or |ω| < ω1 < ω2 < |ω| Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear systems L with Η(ω) = 0 in parts of the frequency domain (= removal of some particular frequencies) LPF = Low Pass Filter : Η(ω) = 0 when |ω| > ω0 when |ω| < ω0 HPF = High Pass Filter : Η(ω) = 0 BPF = Band Pass Filter (inside band) : Η(ω) = 0 when or |ω| < ω1 < ω2 < |ω| BPF = Band Pass Filter (outside band) : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Filters = time-invariant linear systems L with Η(ω) = 0 in parts of the frequency domain (= removal of some particular frequencies) LPF = Low Pass Filter : Η(ω) = 0 when |ω| > ω0 when |ω| < ω0 HPF = High Pass Filter : Η(ω) = 0 BPF = Band Pass Filter (inside band) : Η(ω) = 0 when or |ω| < ω1 < ω2 < |ω| BPF = Band Pass Filter (outside band) : Η(ω) = 0 A. Dermanis when ω1 < |ω| < ω2 Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : A. Dermanis when then Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : when then When Η(ω) = 0 : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : when then When Η(ω) = 0 : When Η(ω) 0 : A. Dermanis Signals and Spectral Methods in Geoinformatics

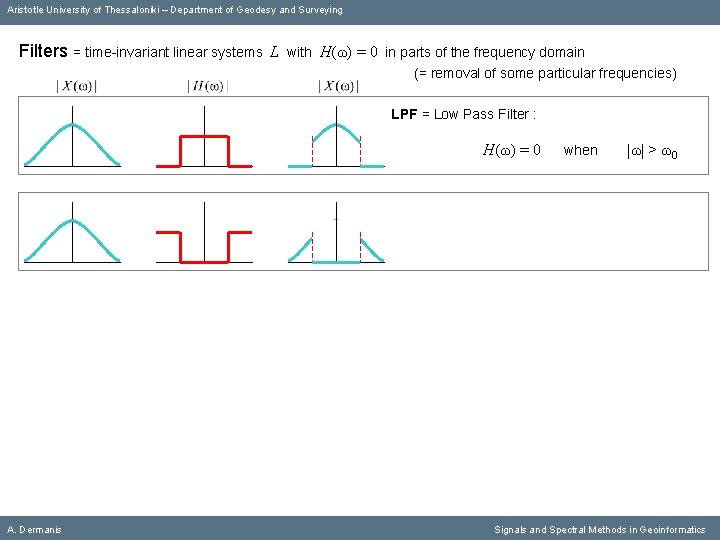
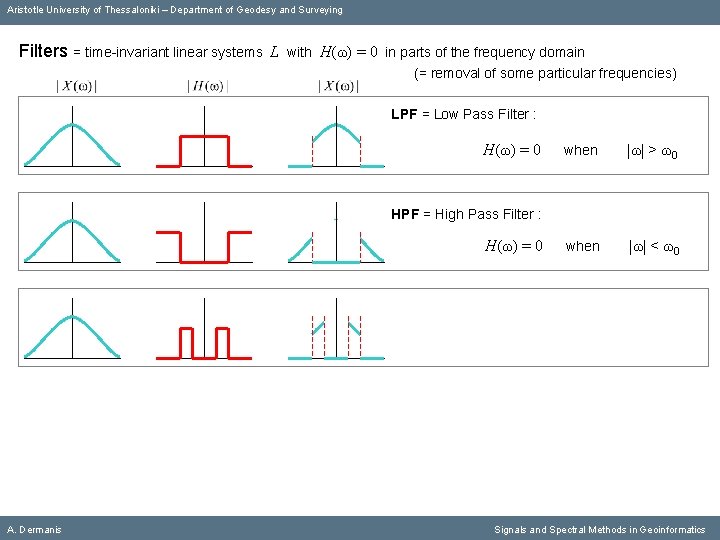
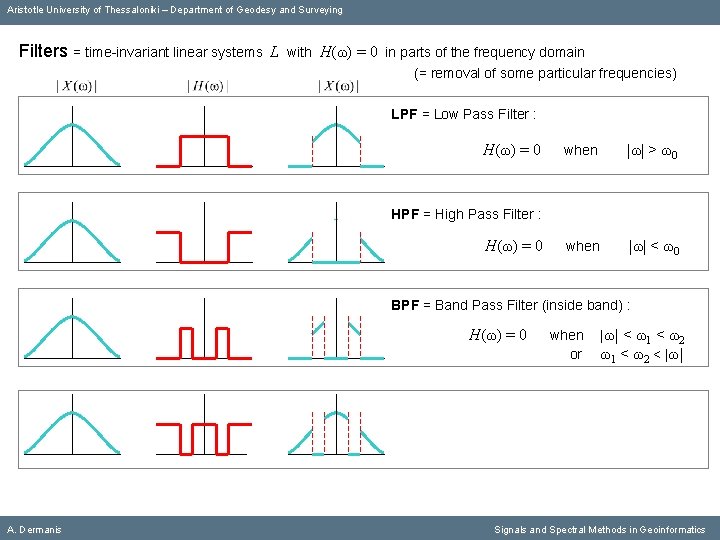
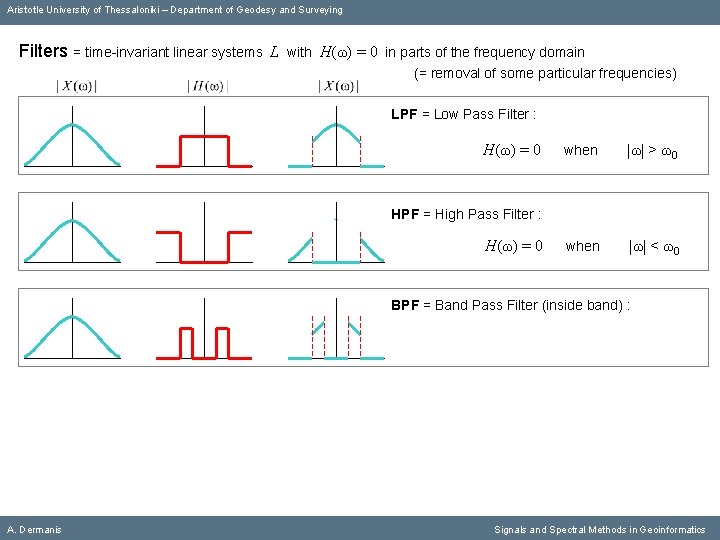
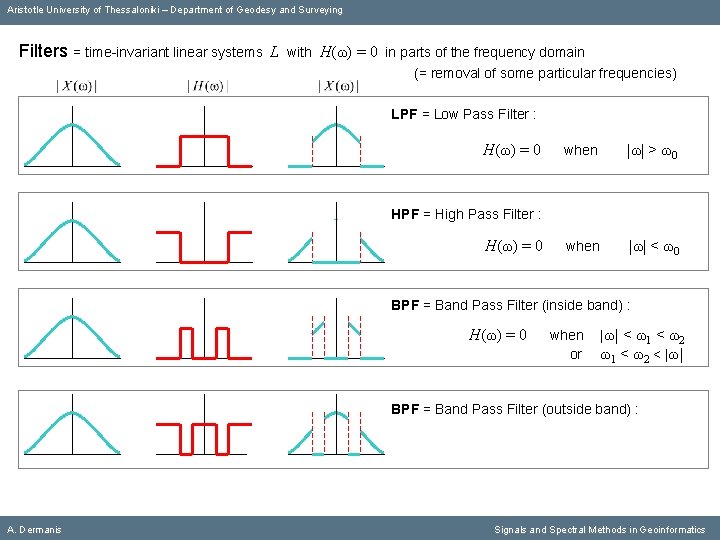
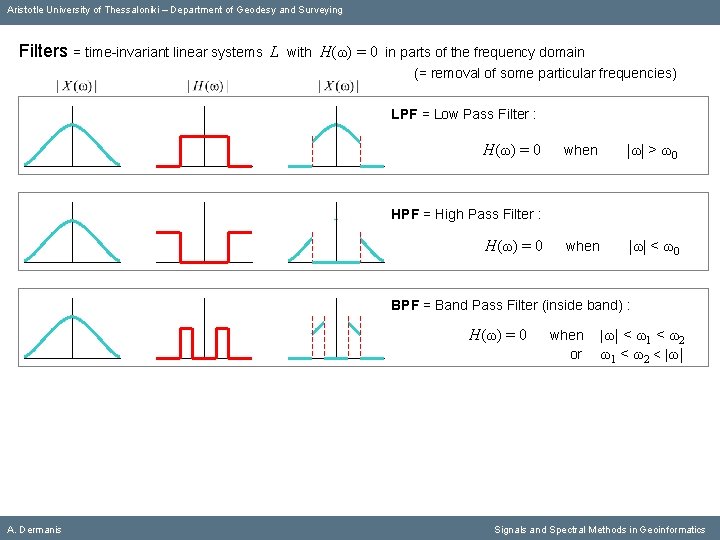
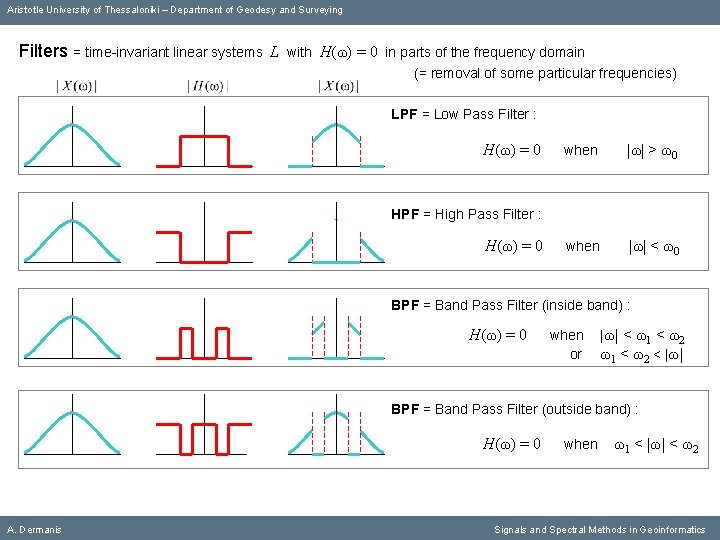
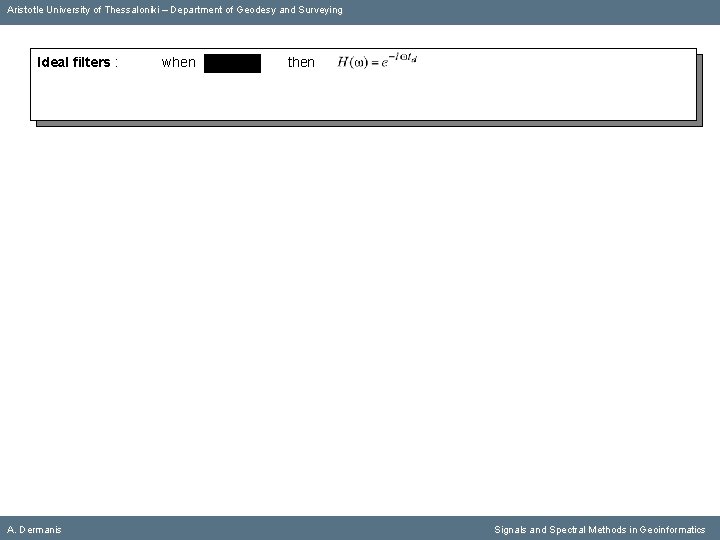
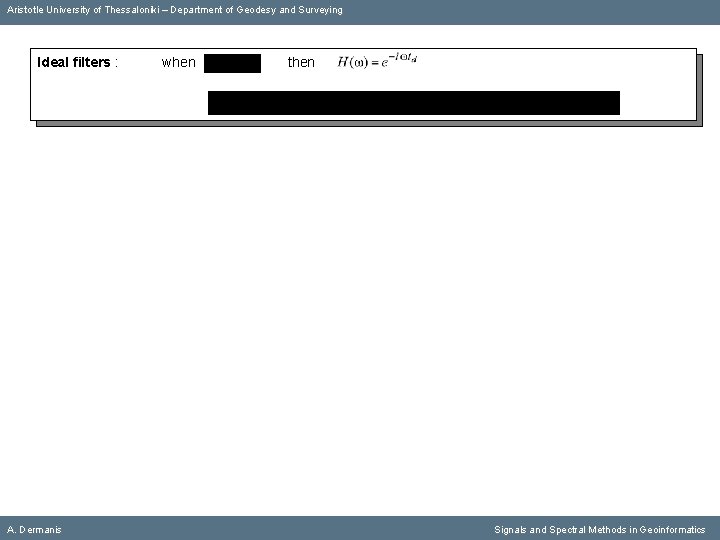
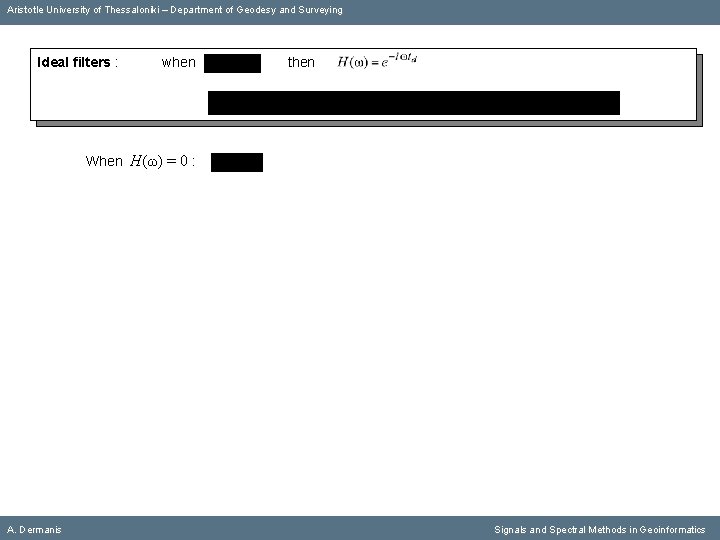
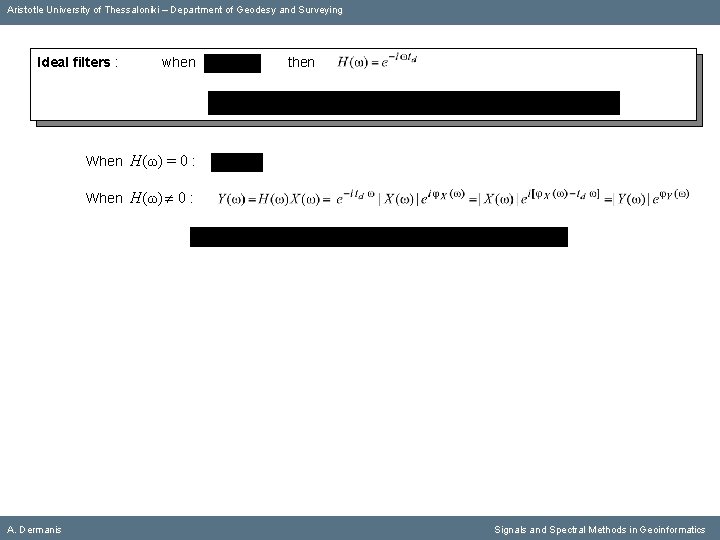
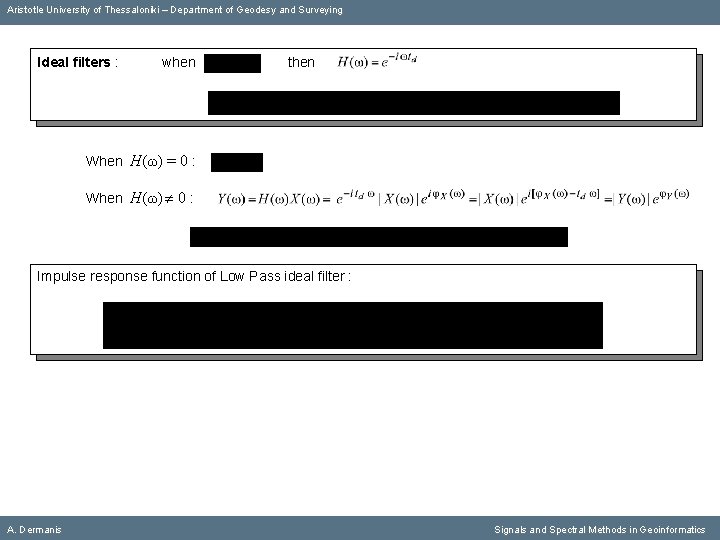
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : when then When Η(ω) = 0 : When Η(ω) 0 : Impulse response function of Low Pass ideal filter : Casual filters (t = time) (instesd of A. Dermanis ) Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Ideal filters : when then When Η(ω) = 0 : When Η(ω) 0 : Impulse response function of Low Pass ideal filter : Casual filters (t = time) (instesd of ) Output y(t) depends only on past ( s t) values s of the input x(s) and not on future values (casuality) A. Dermanis Signals and Spectral Methods in Geoinformatics

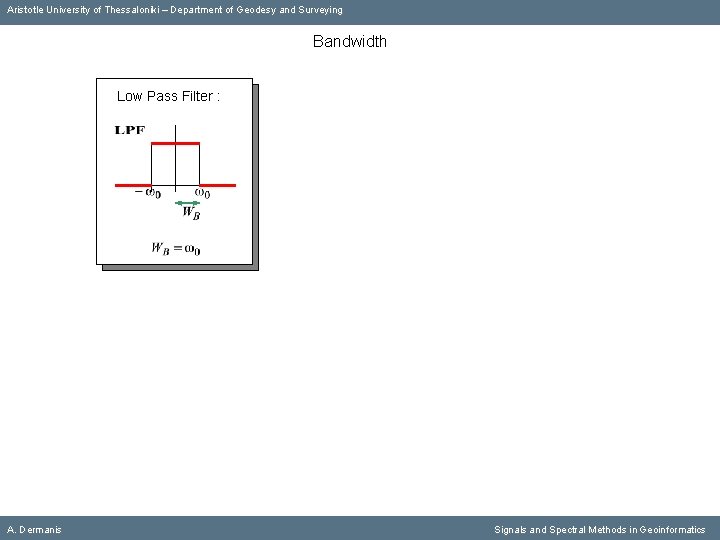
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth A. Dermanis Signals and Spectral Methods in Geoinformatics

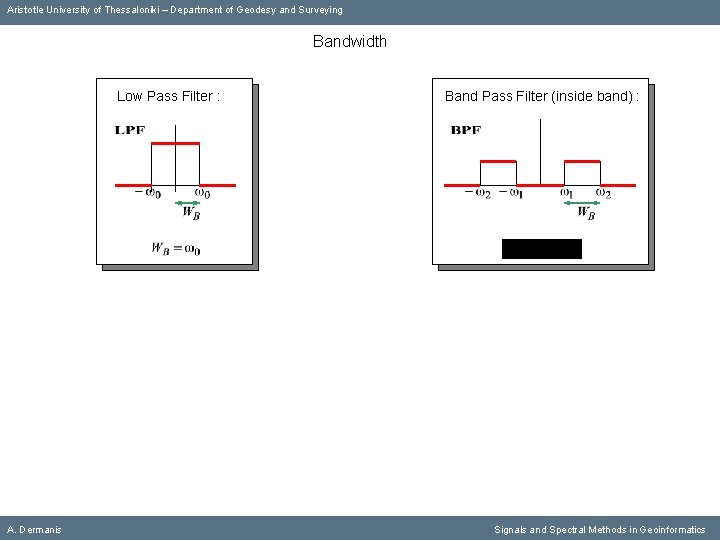
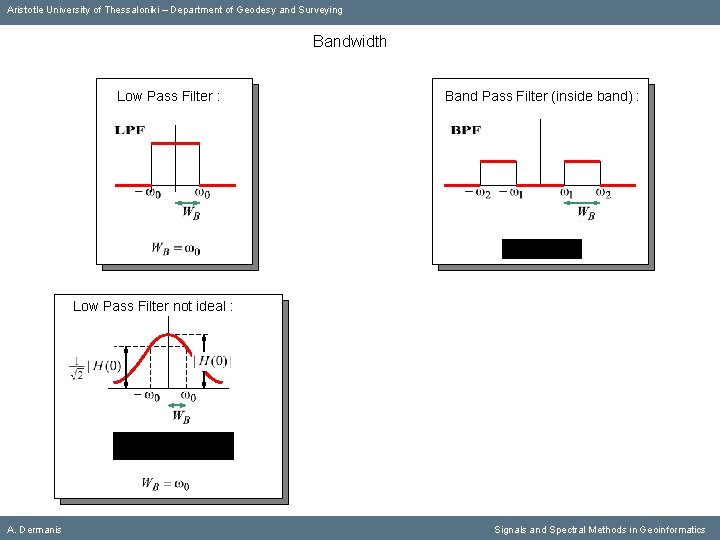
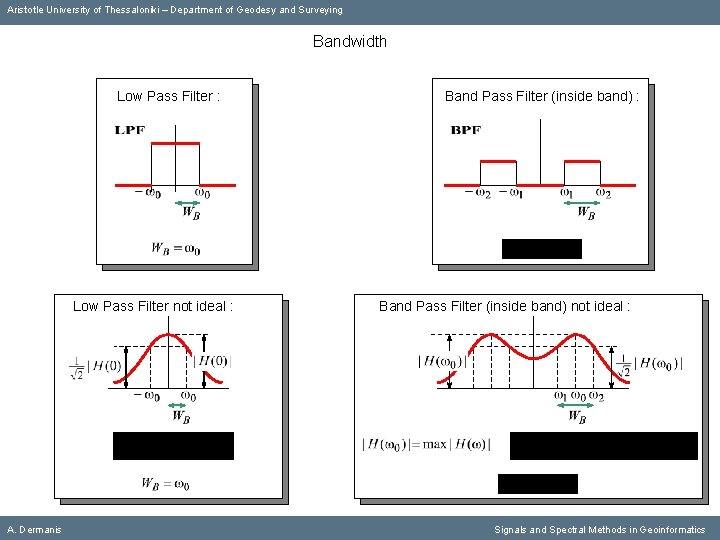
Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth Low Pass Filter : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth Low Pass Filter : A. Dermanis Band Pass Filter (inside band) : Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth Low Pass Filter : Band Pass Filter (inside band) : Low Pass Filter not ideal : A. Dermanis Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying Bandwidth Low Pass Filter : Low Pass Filter not ideal : A. Dermanis Band Pass Filter (inside band) : Band Pass Filter (inside band) not ideal : Signals and Spectral Methods in Geoinformatics

Aristotle University of Thessaloniki – Department of Geodesy and Surveying END A. Dermanis Signals and Spectral Methods in Geoinformatics