Applying Logic Synthesis for Speeding Up SAT Niklas

Applying Logic Synthesis for Speeding Up SAT Niklas Een Alan Mishchenko Niklas Sörensson

Problem Formulation • Given a (combinational) circuit, how do we best clausify it for the CNF-based SAT-solver? Assume given on And-Inverter Graph (AIG) form: Primary Outputs (POs) AIG Primary Inputs (PIs) 2 10/7/2020 . . . gives the freedom to: Contract: Clausify logic - Omit internal signals such that the (functional) (don’t give them a SAT variable) relation between PIs and - Create internal signals POs isnew established. (by circuit simplifying rewrites)

Clausification in the small (“easy”) • How to produce a small set of clauses for 1 -output, kinput subgraphs (“super-gates”) of the AIG for small k: s: – k ≤ 4: Pre-compute and tabulate exact results – 4 < k ≤ 16: Use Minato’s ISOP-algorithm Clausification in the large (hard!) • How to partition AIG into super-gates? • How to handle reconvergence? (the root of all evil) Proposal: Use FPGA-style technology mapping! 3 10/7/2020

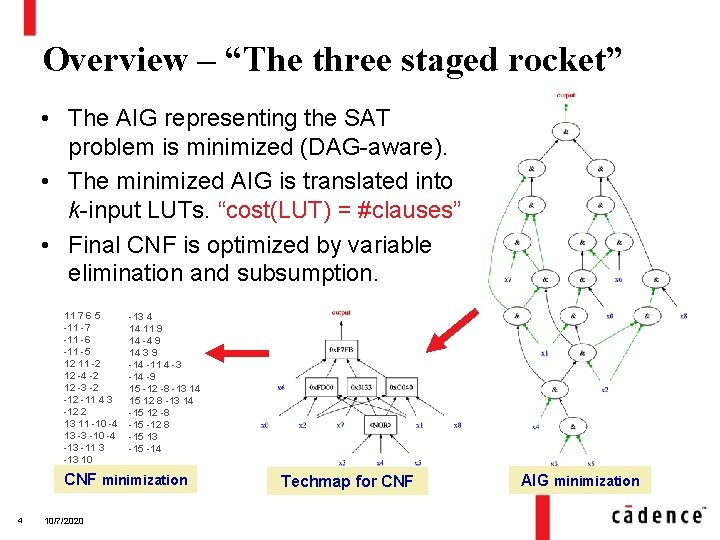
Overview – “The three staged rocket” • The AIG representing the SAT problem is minimized (DAG-aware). • The minimized AIG is translated into k-input LUTs. “cost(LUT) = #clauses” • Final CNF is optimized by variable elimination and subsumption. 11 7 6 5 -11 -7 -11 -6 -11 -5 12 11 -2 12 -4 -2 12 -3 -2 -11 4 3 -12 2 13 11 -10 -4 13 -3 -10 -4 -13 -11 3 -13 10 -13 4 14 11 9 14 -4 9 14 3 9 -14 -11 4 -3 -14 -9 15 -12 -8 -13 14 15 12 8 -13 14 -15 12 -8 -15 -12 8 -15 13 -15 -14 CNF minimization 4 10/7/2020 Techmap for CNF AIG minimization

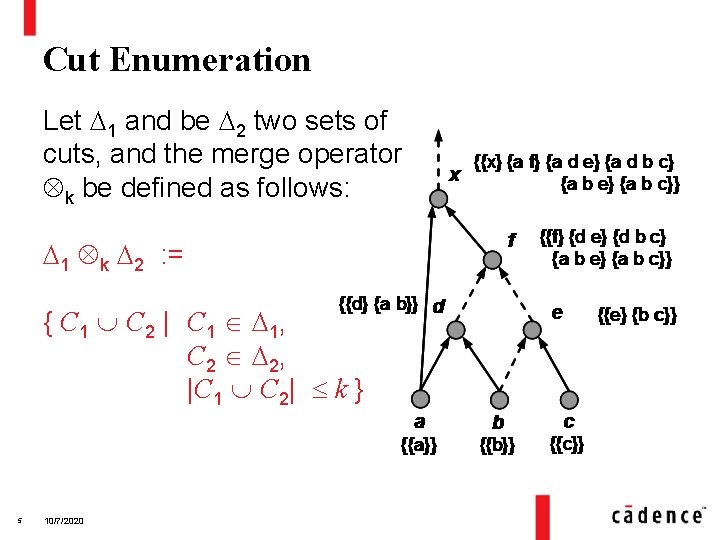
Cut Enumeration Let 1 and be 2 two sets of cuts, and the merge operator k be defined as follows: 1 k 2 : = { C 1 C 2 | C 1 1, C 2 2, |C 1 C 2| k } 5 10/7/2020

DAG-Aware Minimization • Minimizes an AIG taking sharing into account. • Compute “good” AIG representations for each 4 -input function. • Enumerate all cuts: see if cut cone can be replaced by node saving representation. • If time-budget admits: perturb and repeat. 6 10/7/2020

DAG-Aware Minimization: Example 7 10/7/2020

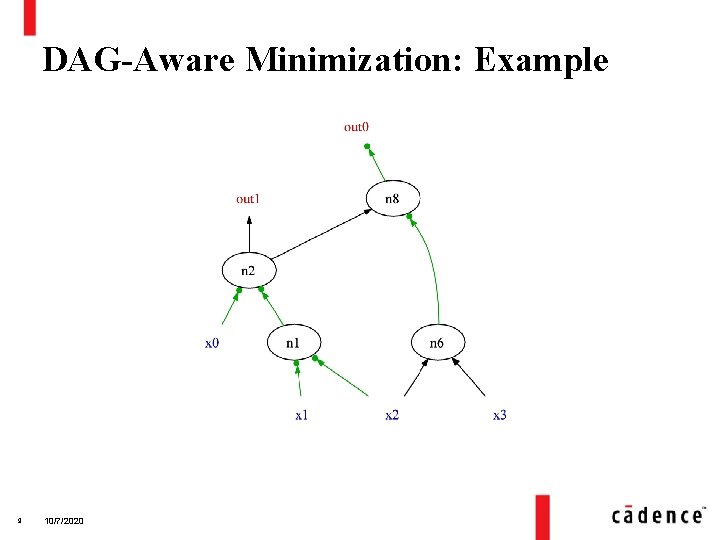
DAG-Aware Minimization: Example 8 10/7/2020

DAG-Aware Minimization: Example 9 10/7/2020

Technology Mapping • Enumerate all k-input cuts (k=4 in example). • Select a cut for each node (= potential LUT). • Outputs from logic will recursively induce a subgraph corresponding to LUT representation. • Area Flow: Estimate the area increase that would result from including a node: cost of node + cost of children estimated number of fanouts • “cost of node = 1” in example on following slides (for simplicity), but “#clauses” in real algorithm. 10 10/7/2020

Techmapping – enumerate cuts Node 17: [req. time=2, fanout est. =1. 5] { { { { 16 15 14 16 15 13 16 15 14 x 2 14 13 x 3 13 } x 2 } x 1 } x 3 x 2 } x 2 x 1 } x 3 x 1 } t t=2 t=2 AF=1. 44 AF=1. 56 AF=1. 11 AF=1. 44 AF=1. 78 AF=1. 33 AF=1. 67 CS=2 CS=3 CS=4 = Arrival Time AF = Area Flow (estimated area required for introducing node) CS = Cut Size 11 10/7/2020

Techmapping – best cut for each node 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 12 10/7/2020 { { { { { x 5 x 5 14 14 14 16 16 14 x 5 15 16 18 27 x 4 x 4 x 2 x 7 x 8 x 1 x 6 x 8 x 4 x 8 x 6 15 19 x 3 x 3 x 1 x 2 x 0 x 1 x 2 x 3 x 1 x 2 x 1 x 0 x 8 x 2 17 x 7 } } } } }

Techmapping – induced subgraph 13: 14: 15: 16: 17: 18: 19: 20: 21: 22: 23: 24: 25: 26: 27: 28: 29: 13 10/7/2020 { { { { { x 5 x 5 14 14 14 16 16 14 x 5 15 16 18 27 x 4 x 4 x 2 x 7 x 8 x 1 x 6 x 8 x 4 x 8 x 6 15 19 x 3 x 3 x 1 x 2 x 0 x 1 x 2 x 3 x 1 x 2 x 1 x 0 x 8 x 2 17 x 7 } } } } }

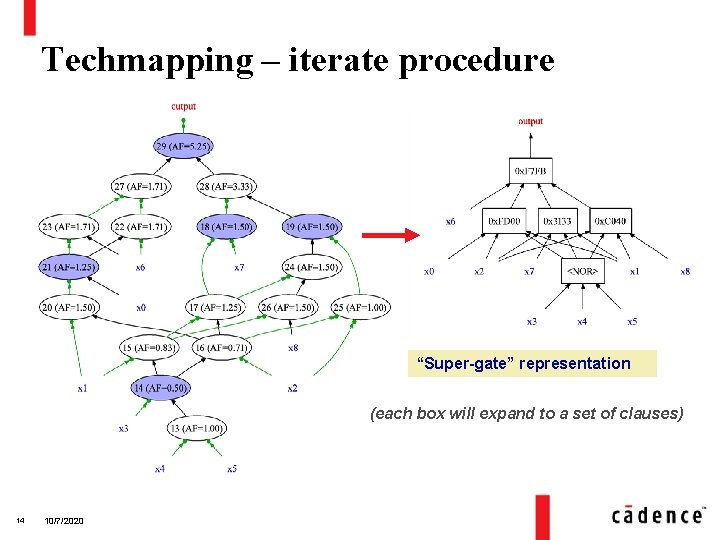
Techmapping – iterate procedure “Super-gate” representation (each box will expand to a set of clauses) 14 10/7/2020

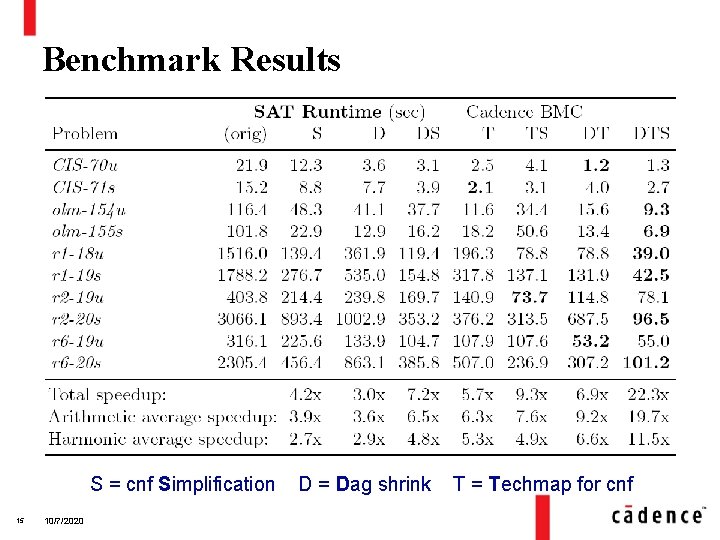
Benchmark Results S = cnf Simplification 15 10/7/2020 D = Dag shrink T = Techmap for cnf

Conclusions • Two techniques from logic synthesis was used: – DAG-aware minimization – Technology mapping (adapted for CNF generation) • Both techniques contributed to speed-ups • Orthogonal to CNF-based preprocessing • For BMC problems, the speedup was ~10 x. 16 10/7/2020