Mini Sat 1 14 Niklas Een and Niklas

Outline • • Introduction Data structure Implementation Conclusion

Introduction • SAT problem: – Given a CNF, find an assignment of variables that

Introduction • DPLL SAT solving: – – Branching Unit propagation Backtracking Learning

Data Structure • Class Vec – Like vector in C++ – In Global. h

Data Structure • Class Clause – In Solver. Types. h – Cannot be used

$Main. c int main(int argc, char** argv){ Solver S; // declare parse_DIMACS(in, S); //$

S. new. Var() (1 + 2 + 3) Watcher list 0 1 2 3

Watcher list C 1: (a’ + b + c) a a’ b b’ c

simplify. DB a a’ b b’ c c’ d d’ a= 1 C 5:

Assignment C 1: (a’ + b + c) C 2: (a + c +

Assignment C 1: (a’ + b + c) C 2: (c + a +

Assignment C 1: (a’ + b + c) C 2: (c + d +

Assignment C 1: (a’ + b + c) C 2: (d + c +

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; i j

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; ws. shrink(i

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; C 3

propagate() C 1: (a’ + b + c) C 2: (d + c +

analyze – UIP: Unique Implication Point • In a cut that there is only

analyze C 1: (a’ + b + c) trail: a’ , b’ , c’

reduce. DB • Remove half of the learnt clauses, minus the clauses locked by

Conclusion • A lot has to be done and traced • Need to learn

Slides: 46

Download presentation

Mini. Sat 1. 14 Niklas Een, and Niklas Sorensson Presenter: Cheng-Shen Han

Outline • • Introduction Data structure Implementation Conclusion

Introduction • SAT problem: – Given a CNF, find an assignment of variables that makes at least one literal true in each clause Literal Clause (disjunction) (a + ¬b)(b + ¬c + d)(¬d) ∧. . . CNF (conjunction of clauses)

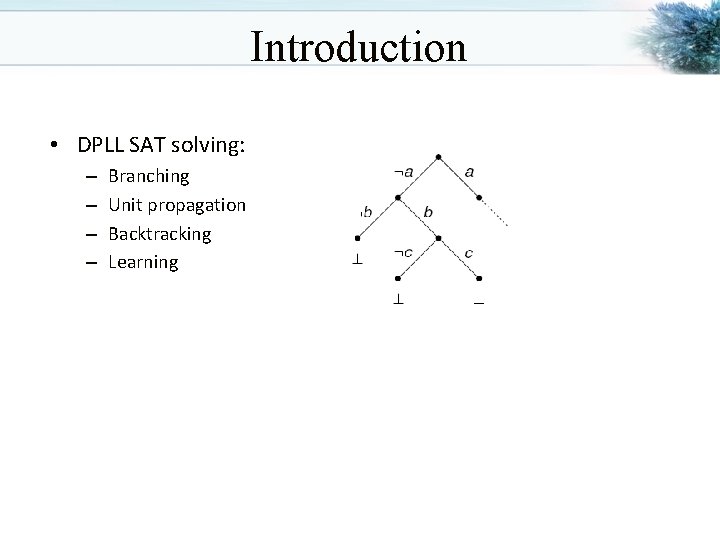
Introduction • DPLL SAT solving: – – Branching Unit propagation Backtracking Learning

Outline • • Introduction Data structure Implementation Conclusion

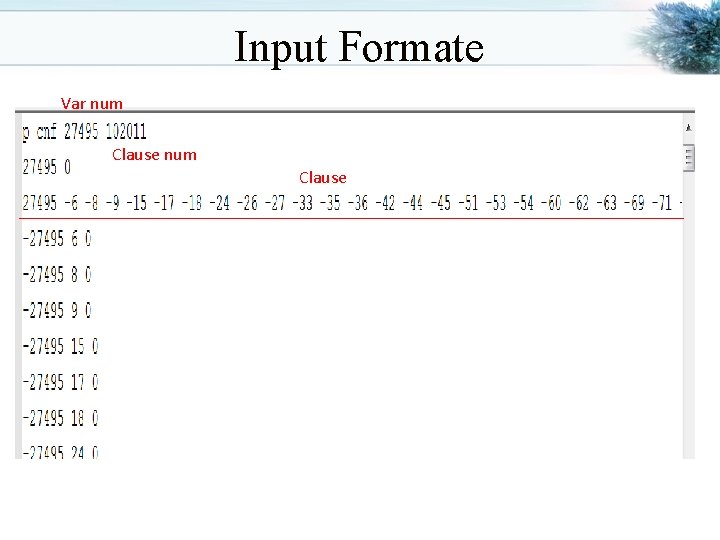
Input Formate Var num Clause

Data Structure • Class Vec – Like vector in C++ – In Global. h • Class lbool – In Global. h • Var – typedef int Var – In Solver. Types. h • Class Lit – – – In Solver. Types. h explicit Lit(Var var, bool sgn = false) : x((var+var) + (int)sgn) {} (1 + 2’) 1 - 1 => 0 => (0 +0 ) + 0 = 0 2 - 1 => (1 + 1) + 1 = 3

Data Structure • Class Clause – In Solver. Types. h – Cannot be used directly (doesn't allocate enough memory) – Clause_new() • Class GClause – In Solver. Types. h – Either a pointer to a clause or a literal.

Outline • • Introduction Data structure Implementation Conclusion

$Main. c int main(int argc, char** argv){ Solver S; // declare parse_DIMACS(in, S); //$

Main. c int main(int argc, char** argv){ Solver S; // declare parse_DIMACS(in, S); // pareser S. new. Var(); S. add. Clause(); S. solve(); // solver }

S. new. Var() (1 + 2 + 3) Watcher list 0 1 2 3 4 5 watches: 'watches[lit]' is a list of constraints watching 'lit' (will go there if literal becomes true). reason: 'reason[var]' is the clause that implied the variables current value, or 'NULL' if none. assigns: The current assignments (lbool: s stored as char: s). level: 'level[var]' is the decision level at which assignment was made. activity order analyze_seen

S. add. Clause()

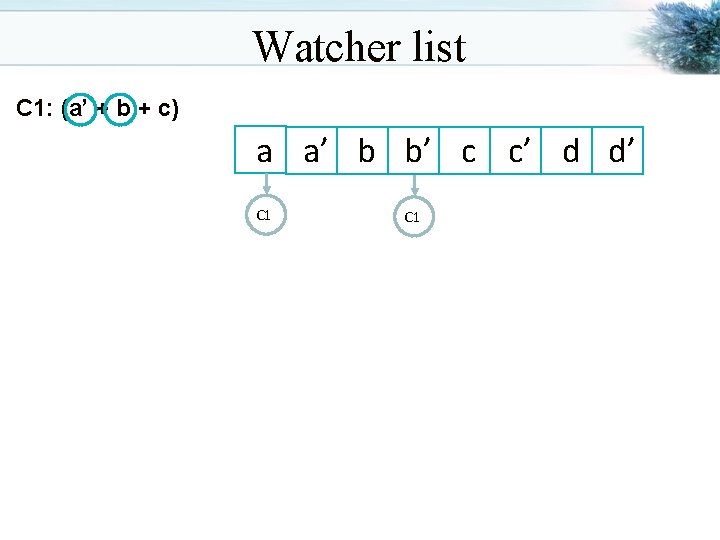
Watcher list C 1: (a’ + b + c) a a’ b b’ c c’ d d’ C 1

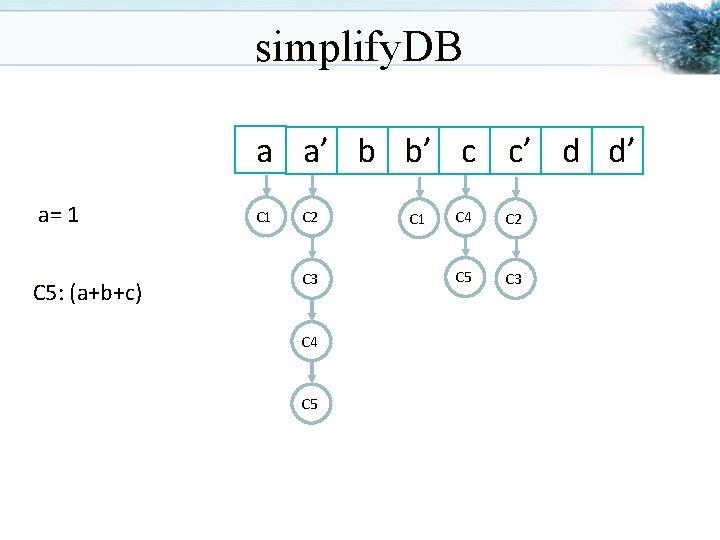
simplify. DB a a’ b b’ c c’ d d’ a= 1 C 5: (a+b+c) C 1 C 2 C 3 C 4 C 5 C 1 C 4 C 2 C 5 C 3

search()

Assignment assume enqueue propagate

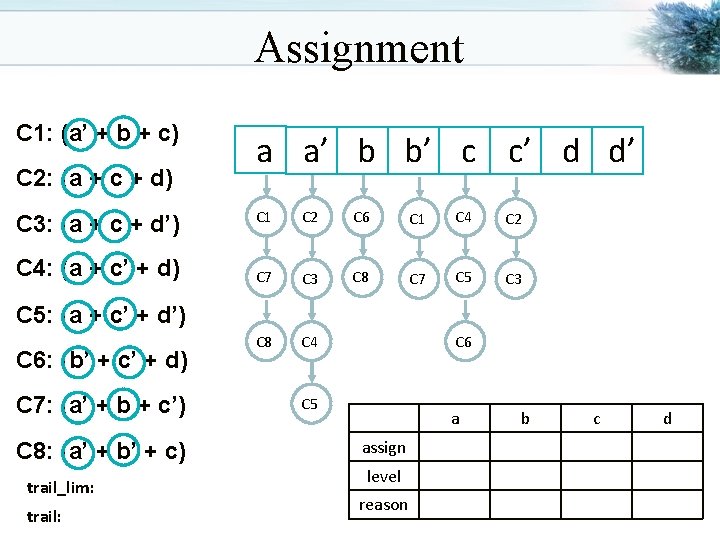
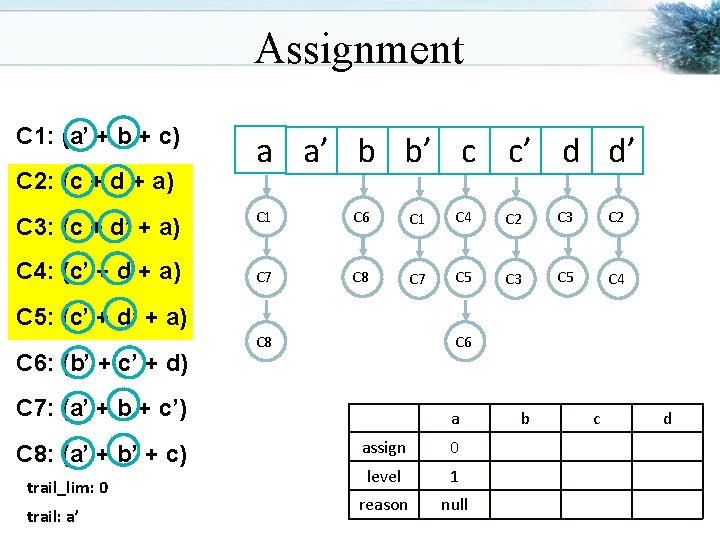
Assignment C 1: (a’ + b + c) C 2: (a + c + d) C 3: (a + c + d’) C 4: (a + c’ + d) a a’ b b’ c c’ d d’ C 1 C 2 C 6 C 1 C 4 C 2 C 7 C 3 C 8 C 7 C 5 C 3 C 8 C 4 C 5: (a + c’ + d’) C 6: (b’ + c’ + d) C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: trail: C 6 C 5 a assign level reason b c d

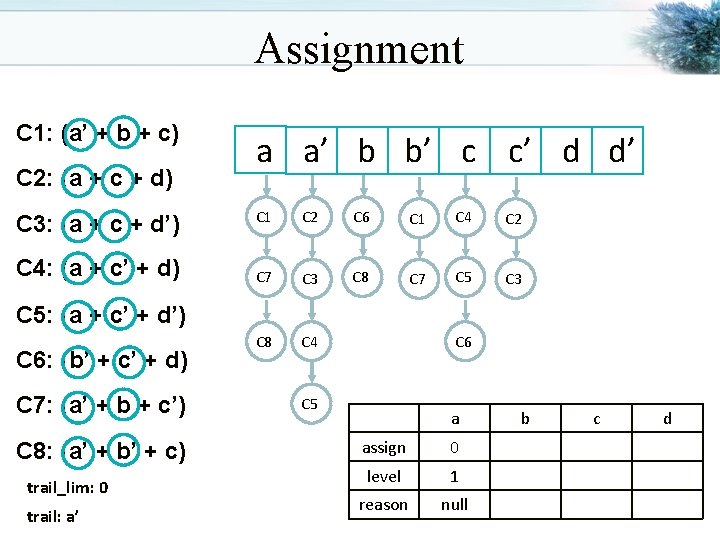
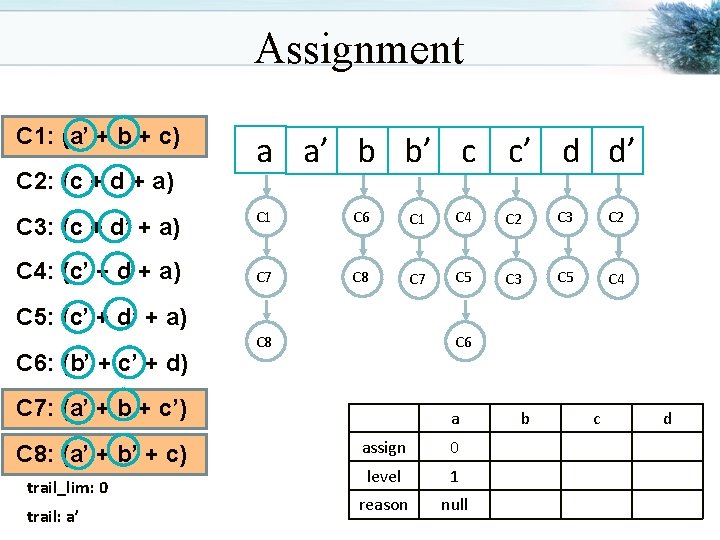
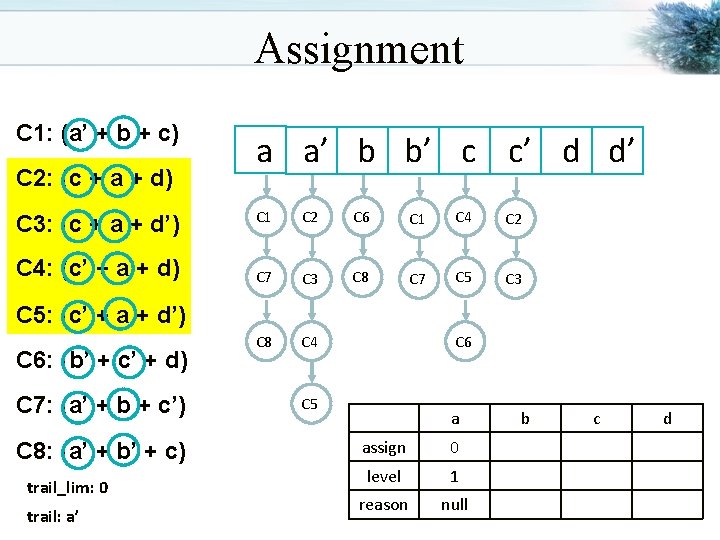
Assignment C 1: (a’ + b + c) C 2: (c + a + d) C 3: (c + a + d’) C 4: (c’ + a + d) a a’ b b’ c c’ d d’ C 1 C 2 C 6 C 1 C 4 C 2 C 7 C 3 C 8 C 7 C 5 C 3 C 8 C 4 C 5: (c’ + a + d’) C 6: (b’ + c’ + d) C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: 0 trail: a’ C 6 C 5 a assign 0 level 1 reason null b c d

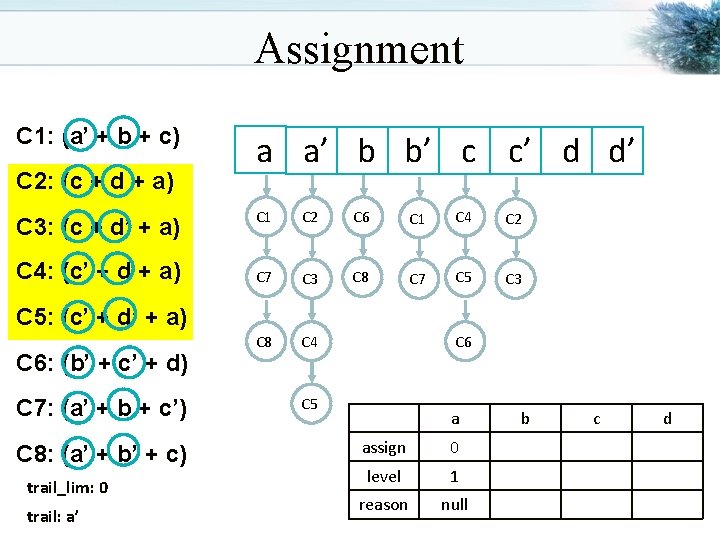
Assignment C 1: (a’ + b + c) C 2: (c + d + a) C 3: (c + d’ + a) C 4: (c’ + d + a) a a’ b b’ c c’ d d’ C 1 C 2 C 6 C 1 C 4 C 2 C 7 C 3 C 8 C 7 C 5 C 3 C 8 C 4 C 5: (c’ + d’ + a) C 6: (b’ + c’ + d) C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: 0 trail: a’ C 6 C 5 a assign 0 level 1 reason null b c d

Assignment C 1: (a’ + b + c) C 2: (c + d + a) C 3: (c + d’ + a) C 4: (c’ + d + a) a a’ b b’ c c’ d d’ C 1 C 6 C 1 C 4 C 2 C 3 C 2 C 7 C 8 C 7 C 5 C 3 C 5 C 4 C 5: (c’ + d’ + a) C 6: (b’ + c’ + d) C 8 C 6 C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: 0 trail: a’ a assign 0 level 1 reason null b c d

Assignment C 1: (a’ + b + c) C 2: (d + c + a) C 3: (d’ + c + a) C 4: (c’ + d + a) a a’ b b’ c c’ d d’ C 1 C 6 C 1 C 4 C 2 C 3 C 2 C 7 C 8 C 7 C 5 C 3 C 5 C 4 C 5: (c’ + d’ + a) C 6: (b’ + c’ + d) C 8 C 6 C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: 0 , 1 , 2 trail: a’ , b’ , c’ a b c assign 0 0 0 level 1 2 3 reason null d

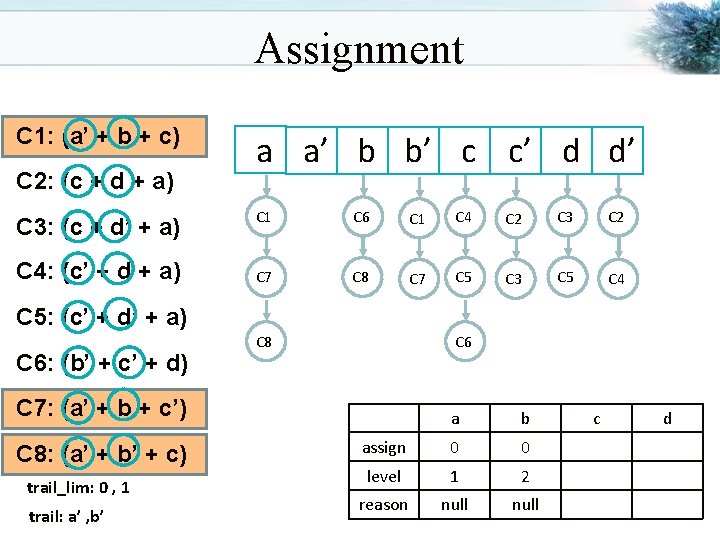
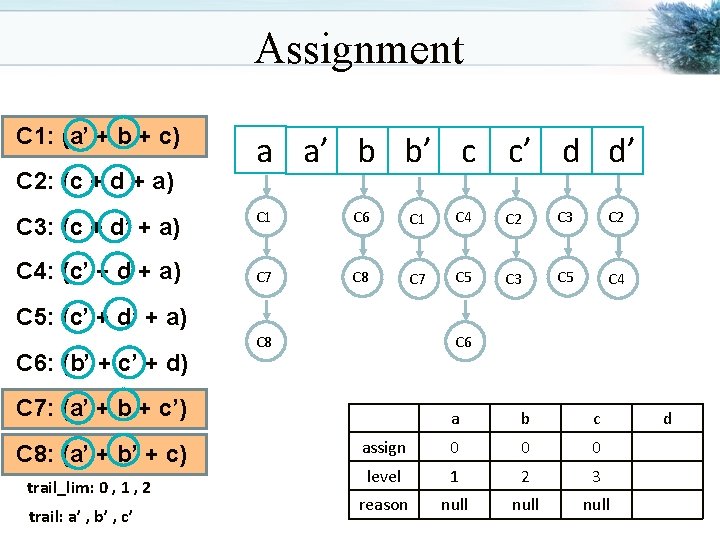
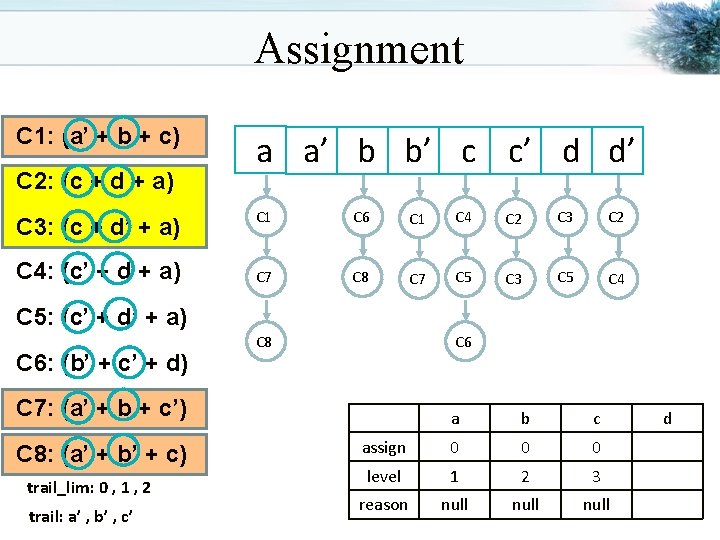
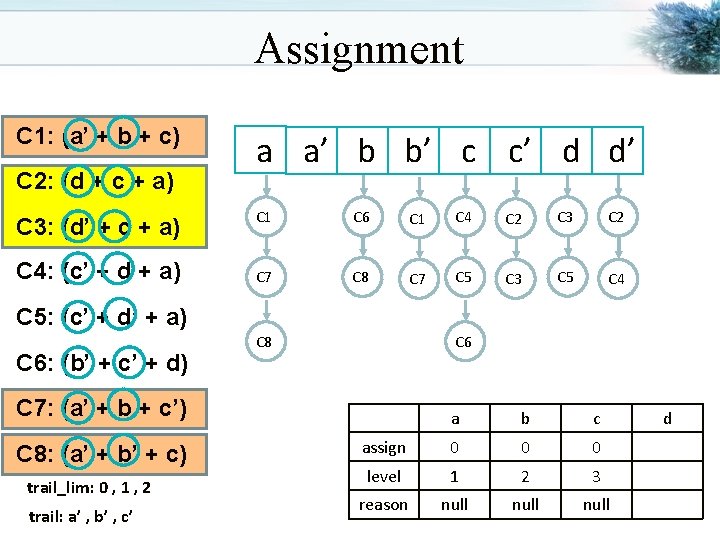
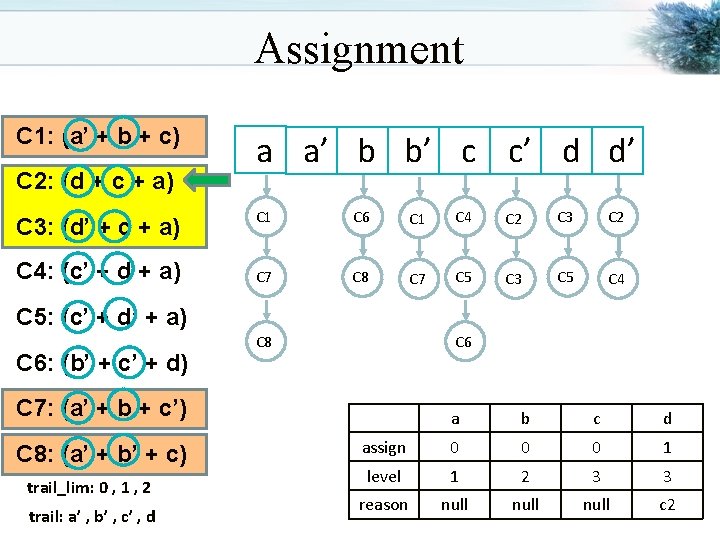
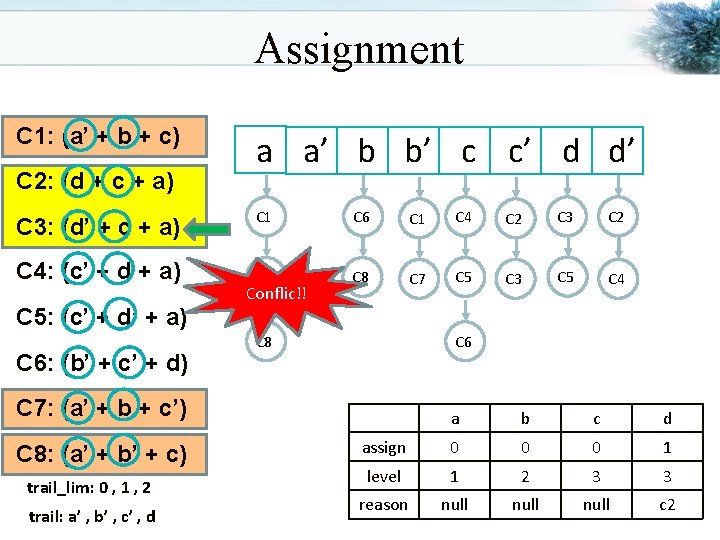
Assignment C 1: (a’ + b + c) C 2: (d + c + a) C 3: (d’ + c + a) C 4: (c’ + d + a) C 5: (c’ + d’ + a) C 6: (b’ + c’ + d) a a’ b b’ c c’ d d’ C 1 C 6 C 1 C 4 C 2 C 3 C 2 C 7 C 8 C 7 C 5 C 3 C 5 C 4 Conflic!! C 8 C 6 C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: 0 , 1 , 2 trail: a’ , b’ , c’ , d a b c d assign 0 0 0 1 level 1 2 3 3 reason null c 2

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; i j C 1 New. W C 3 SAT C 5 IMPLY

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; i j C 3 New. W C 3 SAT C 5 IMPLY

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; i j C 3 New. W C 5 SAT C 5 IMPLY

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; ws. shrink(i - j); i j C 3 New. W C 5 SAT C 5 IMPLY

propagate(): watch list vec<GClause>& ws = watches[index(p)]; GClause* i, * j, *end; C 3 C 5 ws. shrink(i - j);

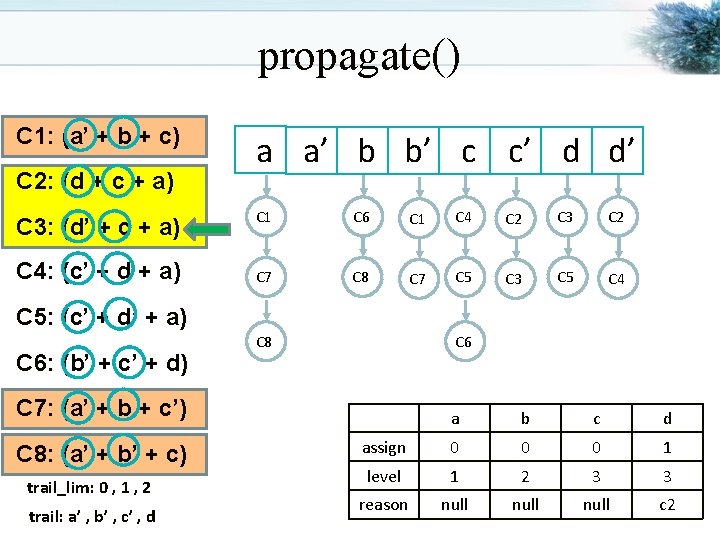
propagate() C 1: (a’ + b + c) C 2: (d + c + a) C 3: (d’ + c + a) C 4: (c’ + d + a) a a’ b b’ c c’ d d’ C 1 C 6 C 1 C 4 C 2 C 3 C 2 C 7 C 8 C 7 C 5 C 3 C 5 C 4 C 5: (c’ + d’ + a) C 6: (b’ + c’ + d) C 8 C 6 C 7: (a’ + b + c’) C 8: (a’ + b’ + c) trail_lim: 0 , 1 , 2 trail: a’ , b’ , c’ , d a b c d assign 0 0 0 1 level 1 2 3 3 reason null c 2

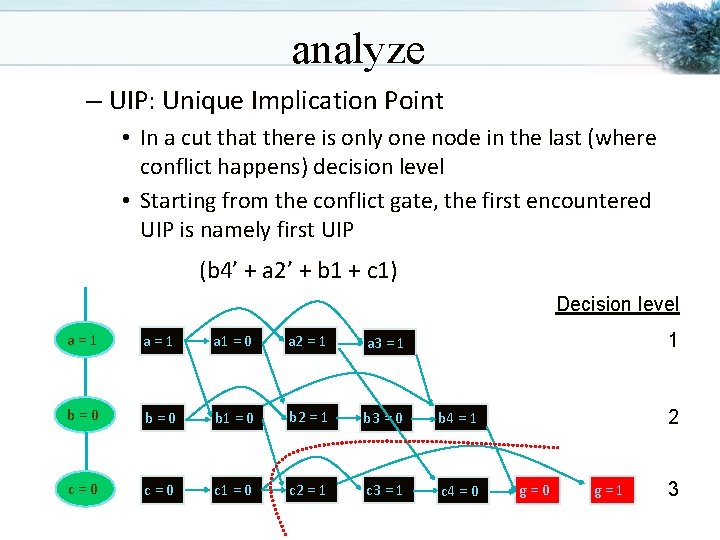
analyze – UIP: Unique Implication Point • In a cut that there is only one node in the last (where conflict happens) decision level • Starting from the conflict gate, the first encountered UIP is namely first UIP (b 4’ + a 2’ + b 1 + c 1) Decision level 1 a=1 a 1 = 0 a 2 = 1 a 3 = 1 b=0 b 1 = 0 b 2 = 1 b 3 = 0 b 4 = 1 c=0 c 1 = 0 c 2 = 1 c 3 = 1 c 4 = 0 2 g=0 g=1 3

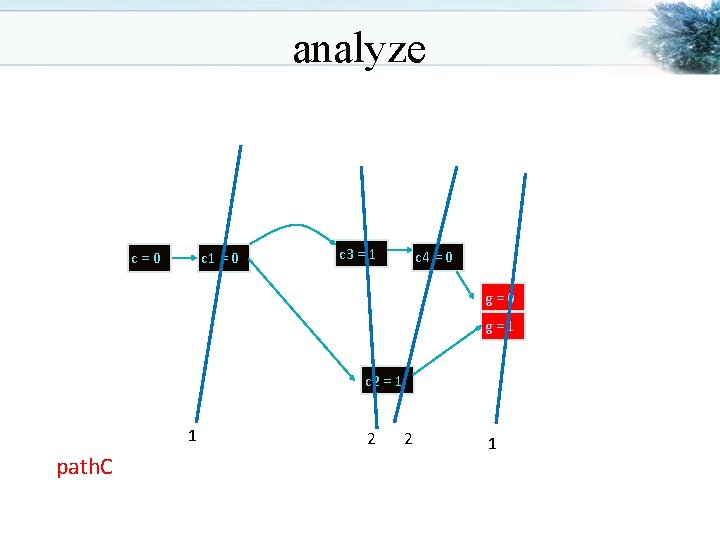
analyze c=0 c 1 = 0 c 3 = 1 c 4 = 0 g=1 c 2 = 1 1 path. C 2 2 1

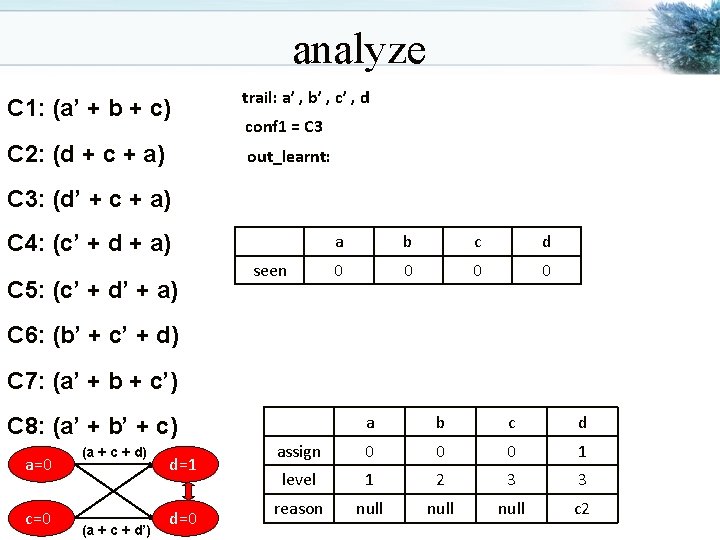
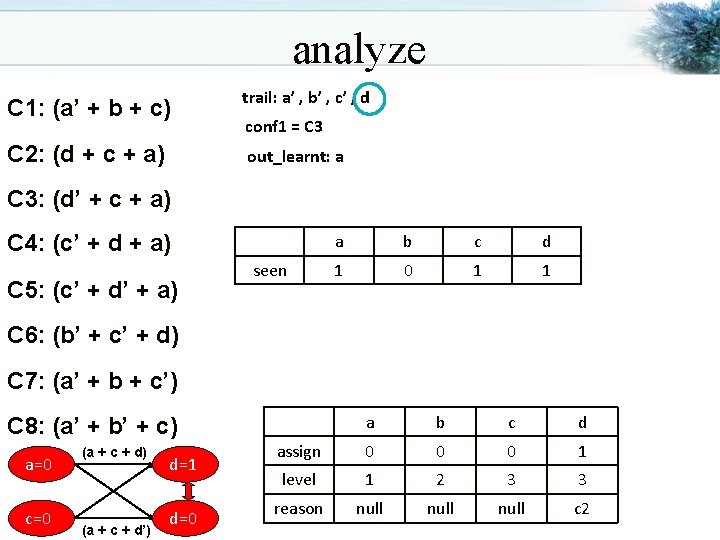
analyze C 1: (a’ + b + c) trail: a’ , b’ , c’ , d C 2: (d + c + a) out_learnt: conf 1 = C 3: (d’ + c + a) C 4: (c’ + d + a) C 5: (c’ + d’ + a) seen a b c d 0 0 C 6: (b’ + c’ + d) C 7: (a’ + b + c’) a b c d assign 0 0 0 1 level 1 2 3 3 reason null c 2 C 8: (a’ + b’ + c) a=0 c=0 (a + c + d) (a + c + d’) d=1 d=0

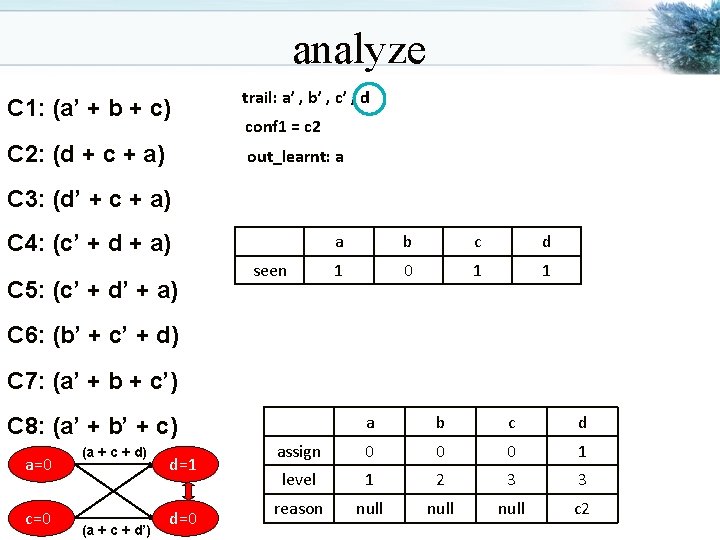
analyze C 1: (a’ + b + c) trail: a’ , b’ , c’ , d C 2: (d + c + a) out_learnt: a conf 1 = C 3: (d’ + c + a) C 4: (c’ + d + a) C 5: (c’ + d’ + a) seen a b c d 1 0 1 1 C 6: (b’ + c’ + d) C 7: (a’ + b + c’) a b c d assign 0 0 0 1 level 1 2 3 3 reason null c 2 C 8: (a’ + b’ + c) a=0 c=0 (a + c + d) (a + c + d’) d=1 d=0

analyze C 1: (a’ + b + c) trail: a’ , b’ , c’ , d C 2: (d + c + a) out_learnt: a conf 1 = c 2 C 3: (d’ + c + a) C 4: (c’ + d + a) C 5: (c’ + d’ + a) seen a b c d 1 0 1 1 C 6: (b’ + c’ + d) C 7: (a’ + b + c’) a b c d assign 0 0 0 1 level 1 2 3 3 reason null c 2 C 8: (a’ + b’ + c) a=0 c=0 (a + c + d) (a + c + d’) d=1 d=0

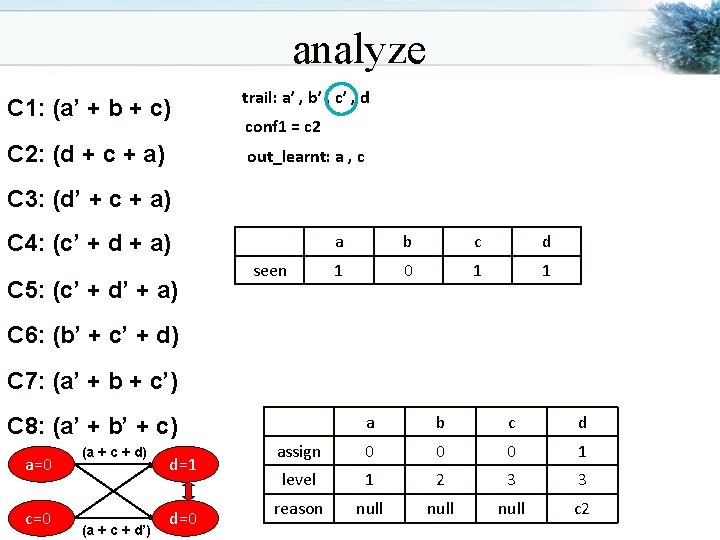
analyze C 1: (a’ + b + c) trail: a’ , b’ , c’ , d C 2: (d + c + a) out_learnt: a , c conf 1 = c 2 C 3: (d’ + c + a) C 4: (c’ + d + a) C 5: (c’ + d’ + a) seen a b c d 1 0 1 1 C 6: (b’ + c’ + d) C 7: (a’ + b + c’) a b c d assign 0 0 0 1 level 1 2 3 3 reason null c 2 C 8: (a’ + b’ + c) a=0 c=0 (a + c + d) (a + c + d’) d=1 d=0

analyze • Conflict clause minimization

reduce. DB • Remove half of the learnt clauses, minus the clauses locked by the current assignment. Locked clauses are clauses that are reason to some assignment. Binary clauses are never removed.

Outline • • Introduction Data structure Implementation Conclusion

Conclusion • A lot has to be done and traced • Need to learn some programming techniques – Compiler knowledge , Memory manage