Anlise Dada uma cadeia de terminais w queremos

Análise • Dada uma cadeia de terminais w, queremos saber se w L(G) ou não. • Se for o caso, poderemos querer achar uma derivação de w. • Um algoritmo que pode nos dizer se w L(G) é um algoritmo de pertinência • o termo análise descreve o modo de achar uma sequência de produções pela qual é derivada w L(G).

• análise óbvia se w está L(G): – construir todas as possíveis (e. g. as mais à esquerda) derivações e verificar se alguma coincide com W. • análise de pesquisa exaustiva • Problemas: – não é eficiente; – é possível que ele nunca termine w L(G). Por cause de produções da forma A B e A

Ambigüidade • Uma gramática livre de contexto G é ambígua se existe w L(G) com no mínimo duas árvores de derivação. • ambiguidade a existência de ≥ 2 derivações à esquerda e à direita.

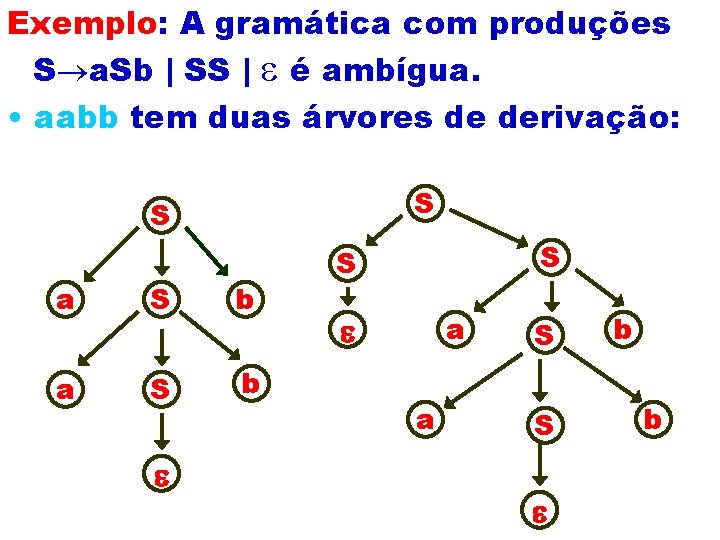
Exemplo: A gramática com produções S a. Sb | SS | é ambígua. • aabb tem duas árvores de derivação: S S a S b S S a a S S b b

Soluções • Re-escrever a gramática tal que exista somente uma análise possível; • Associar regras de precedência (como feito em LP com os + e *) – Esta solução está completamente fora da gramática. • existem exemplos onde é impossível remover a ambiguidade da gramática.

Abigüidade Inerente não-ambígua: • existe uma gramática para L que é não-ambígua; inerentemente ambígua. se toda gramática para L é ambígua. e. g. : L={anbncm|n, m>0} {anbmcm|n, m>0}

Formas Normais • A definição de uma GLC não impõe qualquer restrição no lado direito de uma produção. • Em muitas situações (aplicações) é desejável colocar restrições. • Estudaremos métodos de transformar uma GLC arbitrária numa equivalente que satisfaz certas restrições sobre sua forma.

Forma Normal de Chomsky Uma gramática livre de contexto está na forma normal de Chomsky se todas as produções são da forma A BC ou A a onde A, B, C V e a T.

Forma Normal de Greibach Uma gramática livre de contexto está na forma normal de Greibach se todas as produções tem a forma A a B 1 B 2…Bk para k 0, com A, B 1, Bk V e a T.

Teorema de Normalização Teorema: Para toda GLC G, existe uma GLC G’ na forma normal de Chomsky e uma GLC G’’ na forma normal de Greibach tal que L(G’’)=L(G) - { }

Remoção de Produções Unitárias A B e -Produções Lema: Para qualquer GLC G=(N, , P, S), existe uma GLC G’ sem -produção e sem produção unitária tq L(G’)=L(G) - { }.

Prova Seja P^ o menor conjunto de produções contendo P e fechado sobre as duas regras: (a)Se A B P^ e B P^, então A P^ (b)Se A B P^ e B P^, então A P^

• Podemos construir P^ indutivamente de P adicionando produções para satisfazer (a) e (b). • Seja G^ a gramática G^=(N, , P^, S) como P P^: – L(G) L(G^), obviamente! – mas L(G)=L (G^), porque cada nova produção adicionada pode ser simulada pela produção que a adicionou.

Agora mostramos que para cadeias não nulas x, qualquer derivação S *G^ x de tamanho mínimo não usa -produção nem produção unitária. • Seja x considere a derivação de tamanho mínimo S *G^ x. Suponha para a contradição que A é usada em algum ponto da derivação S * A *x com ou não nulo.

• esta ocorrência de A aparece na derivação quando uma produção da forma B A é aplicada: S m B A n A *x para algum m, n, k 0. • Mas pela regra (a) B está também em P^, e esta produção poderia ter sido usada neste ponto dando uma derivação menor de x: S m B n kx absurdo!

Um argumento similar mostra que produções unitárias não são usadas em derivações de tamanho mínimo. Seja x e considere a derivação de tamanho mínimo S *G^ x. Suponha que A B é usada em algum momento S * A B *x. a ocorrência de B desaparece aplicando a produção B mais tarde: S m A B n B kx

• Mas pela regra (b), A está também em P^ e esta produção poderia ter sido usada dando uma derivação menor para x: S m A n kx • Isto contradiz o tamanho mínimo da derivação. Logo as -produções e produções unitárias podem ser descartadas! qed

Transformando para a forma normal de Chomsky. SPG só consideraremos gramáticas sem - produções e produções unitárias: • Para cada a , introduza um novo não terminal Aa e a produção Aa a, e troque todas as ocorrências de a no lado direito das antigas regras (exceto das regras de forma B a) por Aa.

• Então todas as produções são de uma das duas formas A a ou A B 1 B 2…Bk, k 2 onde os Bi são não terminais. • O conjunto de cadeias terminais não muda, somente temos mais um passo(que antes)para gerar um símbolo terminal.

• Para qualquer produção A B 1 B 2. …Bk com K>2, introduza um novo não terminal C e troque esta produção por duas A B 1 C e C B 2 B 3 …Bk. . • Continue fazendo estas trocas até que todos os lados direitos tenham tamanho no máximo 2.

Exemplo Derive a gramática na forma normal de Chomsky para o conjunto {anbn | n 0} - { } = {anbn | n 1}. • pegue gramática para {anbn | n 0} : S a. Sb| • Removendo as - produções temos: S a. Sb | ab que gera {anbn | n 1}.

• Adicionamos não-terminais A, B e trocamos as produções para: S ASB| AB A a B b • Adicionamos um não-terminal C e trocamos B ASB por S AC C SB. A gramática na forma normal de Chomsky é S AB|AC A a B b C SB