Anderson transitions critical wave functions and conformal invariance

Anderson transitions, critical wave functions, and conformal invariance Ilya A. Gruzberg (University of Chicago) Collaborators: A. Subramaniam (U of C), A. Ludwig (UCSB) F. Evers, A. Mildenberger, A. Mirlin (Karlsruhe) A. Furusaki , H. Obuse (RIKEN, Japan) Papers: PRL 96, 126802 (2006); PRL 98, 156802 (2007); PRB 75, 094204 (2007); Physica E 40, 1404 (2008); PRL 101, 116802 (2008); PRB 78, 245105 (2008) IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Motivations and comments • Metal-insulator transitions (MIT) and critical behavior nearby • Anderson transitions are MIT driven by disorder: clearly posed problem • Physics and math are very far apart: - Existence of metals: obvious to a physicist but an unsolved problem in math - What has been proven rigorously (existence of localized states) was a shock to physicists, when predicted by Anderson • Critical region may be both more interesting and easier to treat rigorously (through stochastic geometry methods: SLE and conformal restriction) IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Metal-insulator transitions • What do we want to find out? - How MIT happens - Phases on both sides - Universal properties (exponents) • Key ingredients: - quantum interference - disorder - interactions: neglect in this talk • Today: importance of boundaries, two dimensions IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

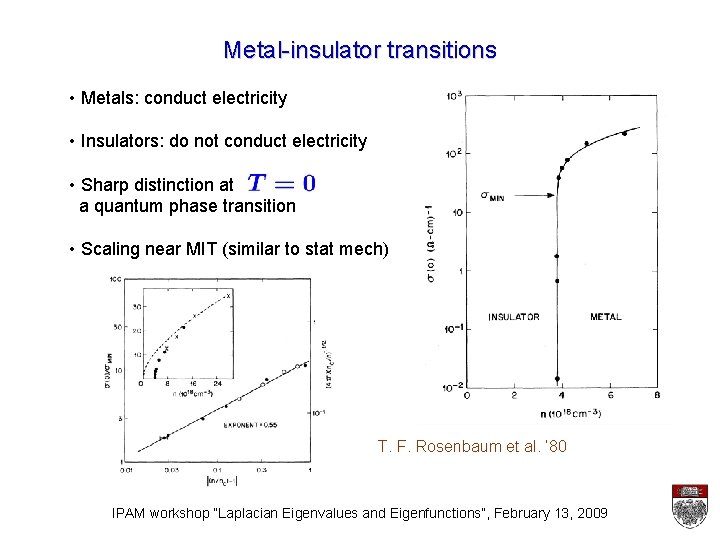
Metal-insulator transitions • Metals: conduct electricity • Insulators: do not conduct electricity • Sharp distinction at a quantum phase transition • Scaling near MIT (similar to stat mech) T. F. Rosenbaum et al. ‘ 80 IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

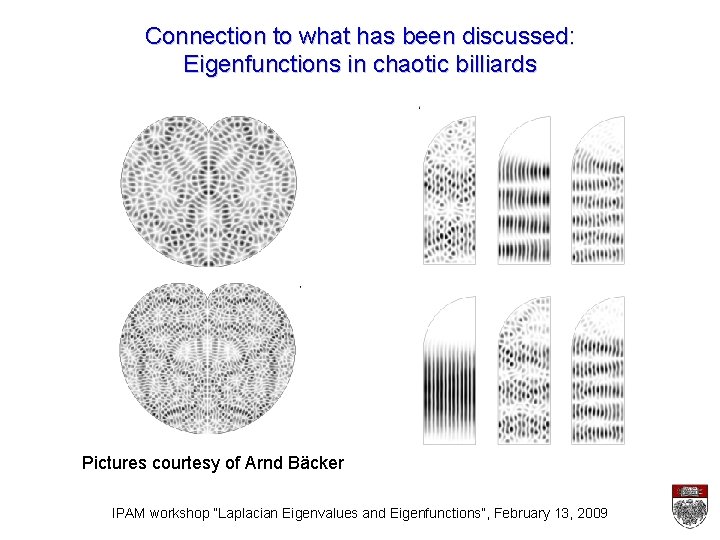
Connection to what has been discussed: Eigenfunctions in chaotic billiards Pictures courtesy of Arnd Bäcker IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

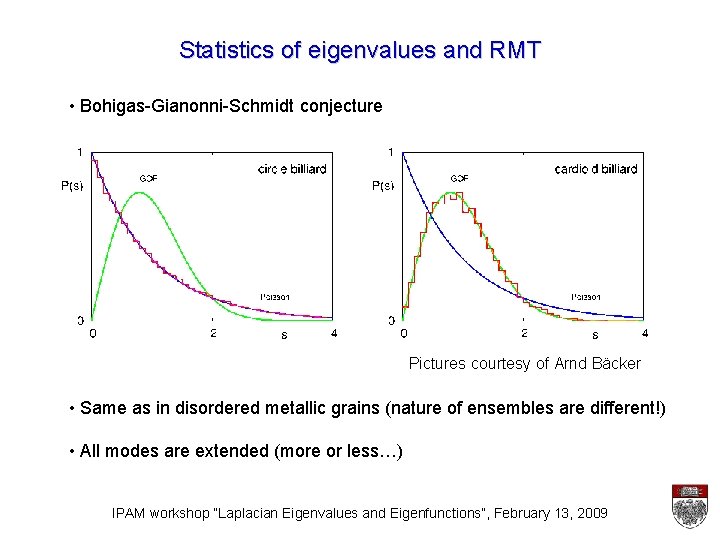
Statistics of eigenvalues and RMT • Bohigas-Gianonni-Schmidt conjecture Pictures courtesy of Arnd Bäcker • Same as in disordered metallic grains (nature of ensembles are different!) • All modes are extended (more or less…) IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

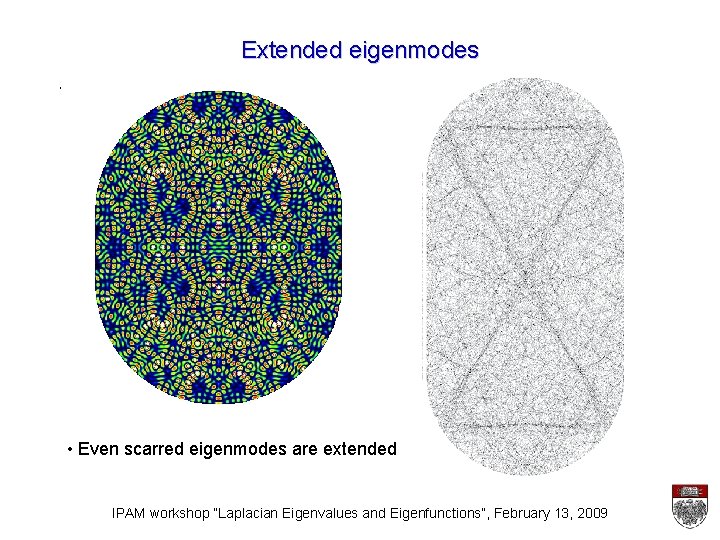
Extended eigenmodes • Even scarred eigenmodes are extended IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Connection to what has been discussed: Eigenfunctions in fractal billiards IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Eigenfunctions in fractal billiards • Some extended, some localized… Is there a transition? Pictures from B. Sapoval, Th. Gobron, A. Margolina, Phys. Rev. Lett. 67, 2974 (1991) • Are there other types of eigenfunctions? IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Problem of localization • Single electron in a random potential (no interactions) • Possibility of a metal-insulator transition (MIT) driven by disorder • Ensemble of disorder realizations: statistical treatment • Classical analogues: waves in random media • More complicated variants (extra symmetries) IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Symmetry classification of disordered electronic systems A. Altland, M. Zirnbauer ‘ 96 • Integer quantum Hall • Spin-orbit metal-insulator transition • Spin quantum Hall • Thermal quantum Hall IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Weak localization • Qualitative semiclassical picture D. Khmelnitskii ‘ 82 G. Bergmann ‘ 84 R. P. Feynman ‘ 48 • Superposition: add probability amplitudes, then square • Interference term vanishes for most pairs of paths IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Weak localization • Paths with self-intersections - Probability amplitudes - Return probability - Enhanced backscattering • Reduction of conductivity L. P. Gor’kov, A. I. Larkin, D. Khmelnitskii ‘ 79 IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

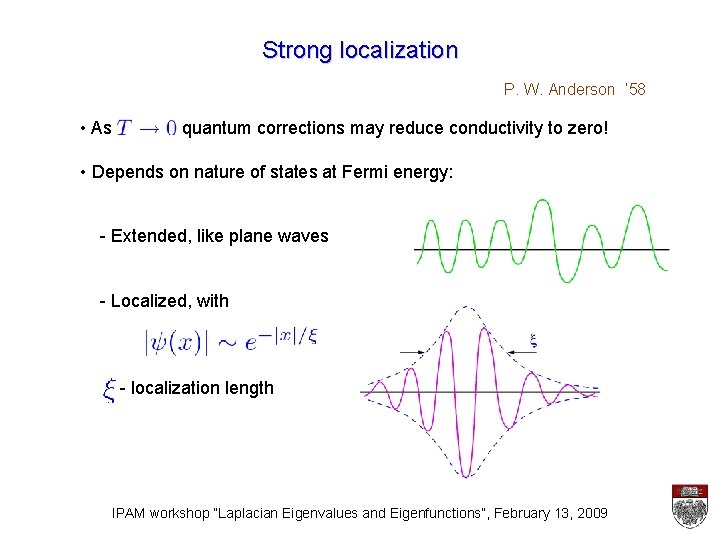
Strong localization P. W. Anderson ‘ 58 • As quantum corrections may reduce conductivity to zero! • Depends on nature of states at Fermi energy: - Extended, like plane waves - Localized, with - localization length IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Strong localization • Nature of states depends on where they are in the spectrum N. F. Mott ‘ 67 • Mobility edge separates extended and localized states • Anderson transition at - Localization length diverges - Density of states smooth: no obvious order parameter or broken symmetry IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Anderson transitions • Scaling theory of localization E. Abrahams et al. “Gang of four” ‘ 79 all states are localized! Anderson MIT • Sometimes happens in 2 D: - quantum Hall plateau transition - spin-orbit interactions (symplectic class) • Modern approach: supersymmetric • -model K. B. Efetov ‘ 83 describes metallic grains, gives RMT level statistics IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Anderson transitions • Metal-insulator transitions (MIT) induced by disorder • Quantum phase transitions with highly unconventional properties: no spontaneous symmetry breaking! • Critical wave functions are neither localized nor truly extended, but are complicated scale invariant multifractals characterized by an infinite set of exponents • For most Anderson transitions no analytical results are available, even in 2 D where conformal invariance is expected to provide powerful tools of conformal field theory (CFT) IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

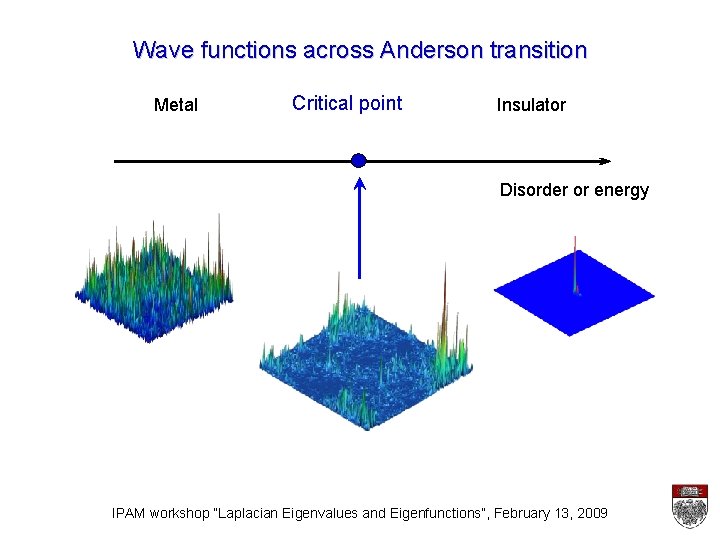
Wave functions across Anderson transition Metal Critical point Insulator Disorder or energy IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Wave function across Anderson transition in 3 D R. A. Roemer IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

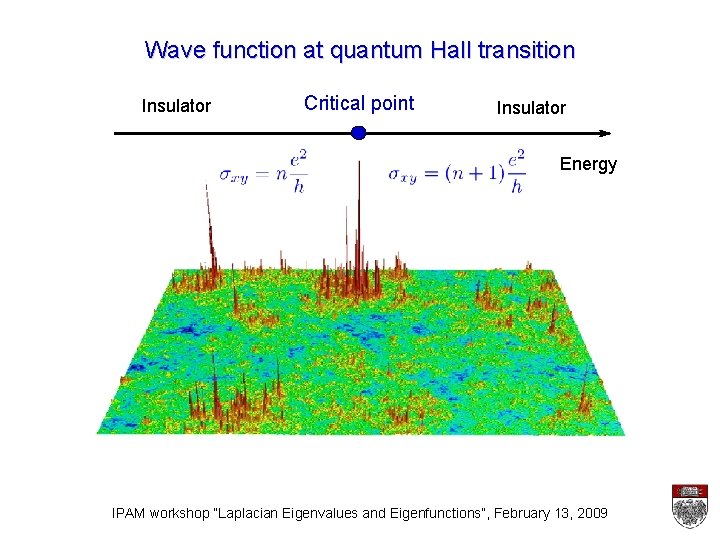
Wave function at quantum Hall transition Insulator Critical point Insulator Energy IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractal wave functions • Anderson transition: - Divergent localization length - No broken symmetry or order parameter F. Wegner `80 C. Castellani, L. Peliti `86 • Moments of the wave function intensity IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractals • “A fractal is a set, a multifractal is a measure” B. Mandelbrot ‘ 74 • Clumpy distribution with density • Self-similarity, scaling • Characterizes a variety of complex systems: turbulence, strange attractors, diffusion-limited aggregation, critical cluster boundaries… • Member of an ensemble • Two way to quantify: scaling of moments and singularity spectrum IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractal moments IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractal moments • Extreme cases • In general IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

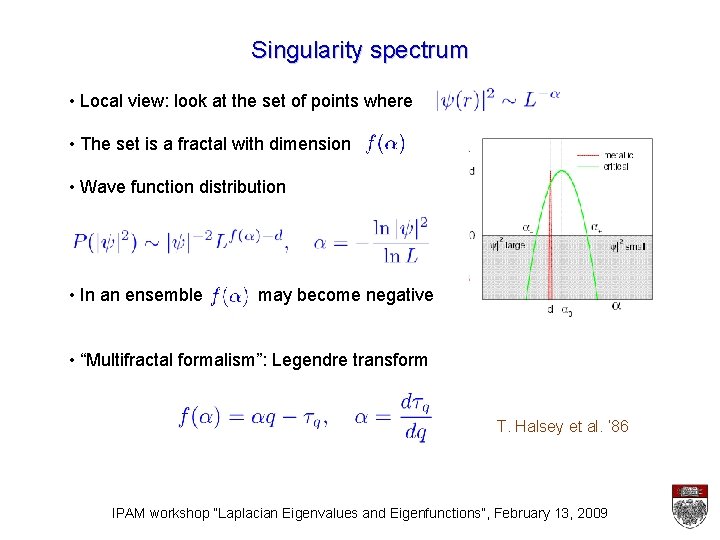
Singularity spectrum • Local view: look at the set of points where • The set is a fractal with dimension • Wave function distribution • In an ensemble may become negative • “Multifractal formalism”: Legendre transform T. Halsey et al. ‘ 86 IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractality and field theory • Anomalous exponents: • In • F. Wegner ‘ 80 - scaling dimensions of operators in a field theory B. Duplantier, A. Ludwig ‘ 91 • Infinity of operators with negative dimensions • corresponds to non-critical DOS • Connection trough Green’s functions and local DOS IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Boundary properties at Anderson transitions • Surface critical behavior has been extensively studied at ordinary critical points, but not for Anderson transitions • Why are boundaries interesting? - practical interest: leads attach to the surface - multifractals with boundaries have not been studied before: we find that the boundaries affect scaling properties even in thermodynamic limit! - in 2 D boundaries provide access to elusive CFT description: we use them to provide direct numerical evidence for presence of conformal invariance IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Boundary multifractality A. Subramaniam et al. , PRL 96, 126802 (2006) • By analogy with critical phenomena expect different scaling behavior near boundaries • “Surface” (boundary) contribution to wave function moments • surface multifractal exponents, distinct from the bulk ones • Can calculate in and other cases IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractality in a finite system A. Subramaniam et al. , PRL 96, 126802 (2006) • Consider IPR for a whole sample, including bulk and surface • Does the boundary matter? • Naive answer: no, the weight of the boundary is down by so expect • This is not correct even in thermodynamic limit! IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Boundary multifractality in (2+e)D A. Subramaniam et al. , PRL 96, 126802 (2006) • Perturbation theory gives ( ) • Singularity spectra IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

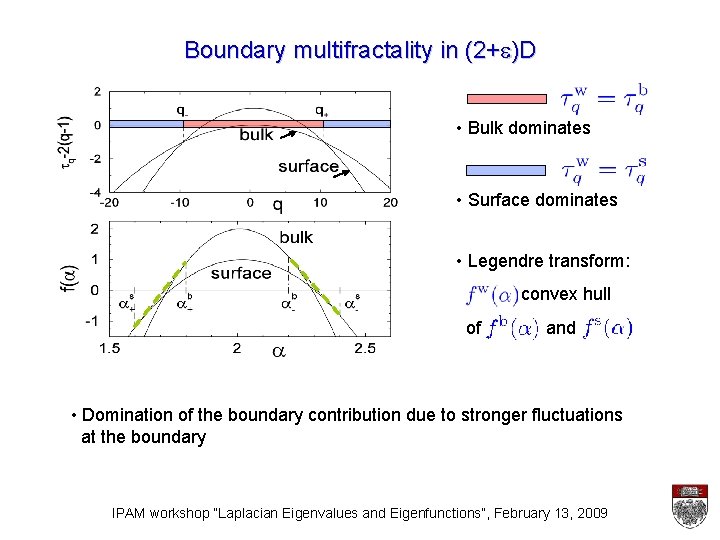
Boundary multifractality in (2+e)D • Bulk dominates • Surface dominates • Legendre transform: convex hull of and • Domination of the boundary contribution due to stronger fluctuations at the boundary IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Boundary multifractality • Domination of the boundary should be a property of multifractals in general • Known case: charge distribution (harmonic measure) on a polymer (and other SLE’s) E. Bettelheim et al. , PRL 95, 170602 (2005) I. Rushkin et al. , J. Phys A 40, 2165 (2007) • What about realistic Anderson transitions? • Investigate numerically for 2 D MIT in the spin-orbit symmetry class • In 2 D Anderson transitions should possess conformal invariance • Can test directly using boundary multifractal scaling of wave functions IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Spin-orbit metal-insulator transition • Spin-orbit metal-insulator transition IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

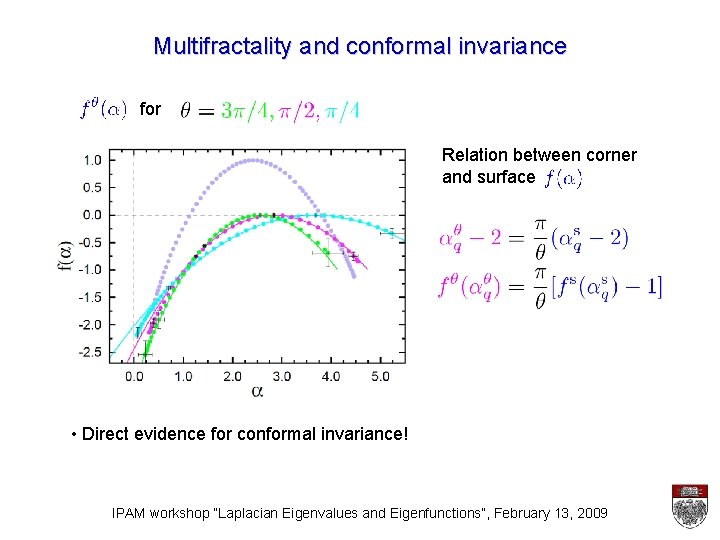
Multifractality and conformal invariance H. Obuse et al. , PRL 98, 156802 (2007) • Critical wave functions in a finite system with corners surface q bulk • Corner multifractality corner L • Anomalous dimensions IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractality and conformal invariance H. Obuse et al. , PRL 98, 156802 (2007) • Assumption: corresponds to a primary operator • Boundary CFT relates corner and surface dimensions: J. Cardy ‘ 84 • Singularity spectrum: IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

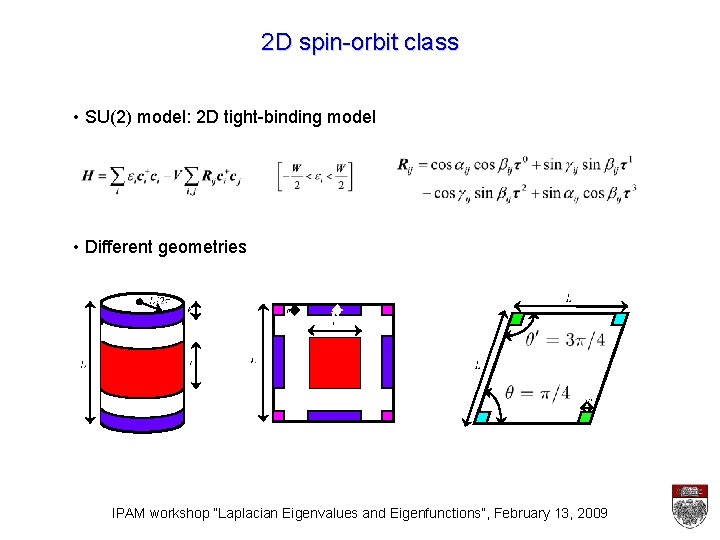
2 D spin-orbit class • SU(2) model: 2 D tight-binding model • Different geometries h IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

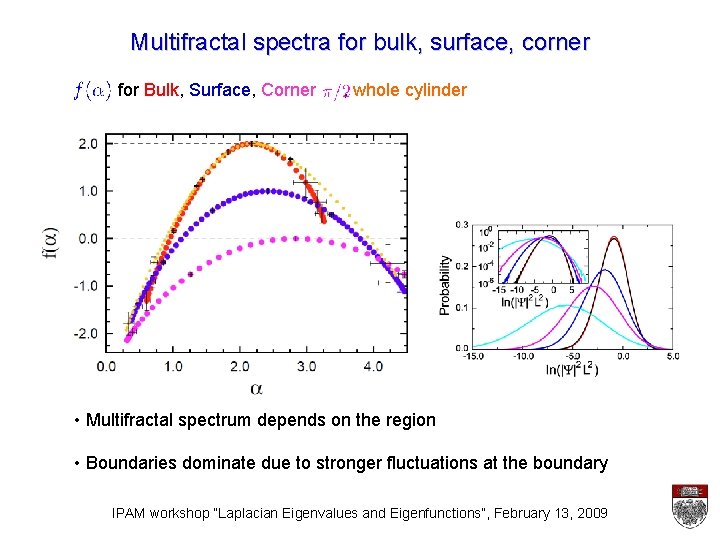
Multifractal spectra for bulk, surface, corner for Bulk, Surface, Corner , whole cylinder • Multifractal spectrum depends on the region • Boundaries dominate due to stronger fluctuations at the boundary IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Multifractality and conformal invariance for Relation between corner and surface • Direct evidence for conformal invariance! IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Theory proposals and conjectured multifractality for the integer quantum Hall transition • Variants of Wess-Zumino (WZ) models on a supergroup (Zirnbauer, Tsvelik, Le. Clair) • Different target spaces (same Lie superalgebra ) • Different proposals for the value of the “level” • A series of conjectures leads to a prediction of exactly parabolic multifractal spectra IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

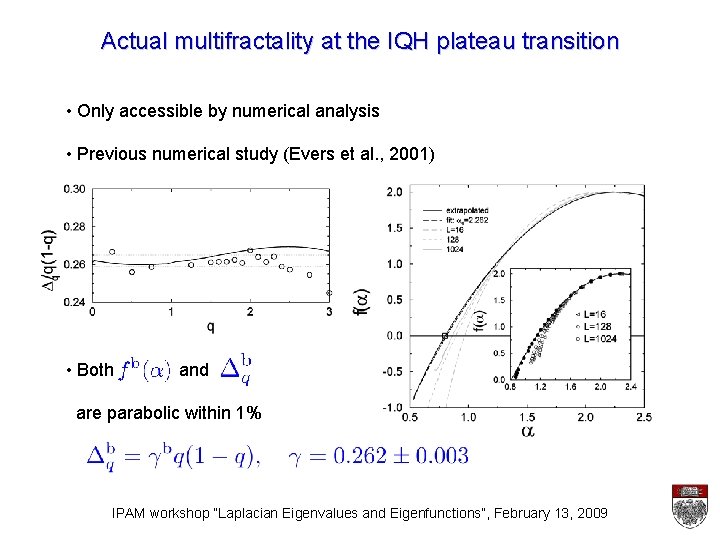
Actual multifractality at the IQH plateau transition • Only accessible by numerical analysis • Previous numerical study (Evers et al. , 2001) • Both and are parabolic within 1% IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

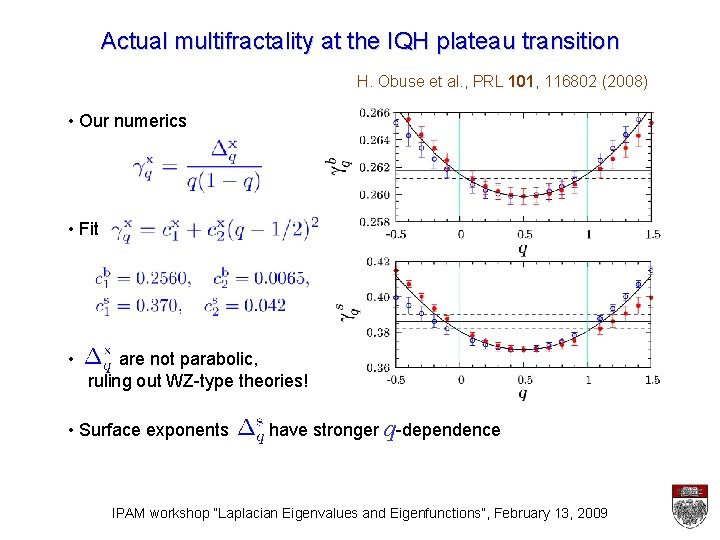
Actual multifractality at the IQH plateau transition H. Obuse et al. , PRL 101, 116802 (2008) • Our numerics • Fit • are not parabolic, ruling out WZ-type theories! • Surface exponents have stronger q-dependence IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

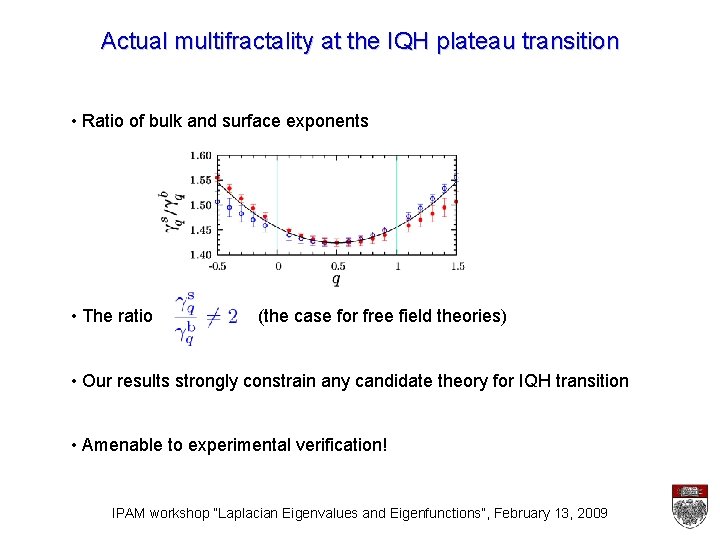
Actual multifractality at the IQH plateau transition • Ratio of bulk and surface exponents • The ratio (the case for free field theories) • Our results strongly constrain any candidate theory for IQH transition • Amenable to experimental verification! IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

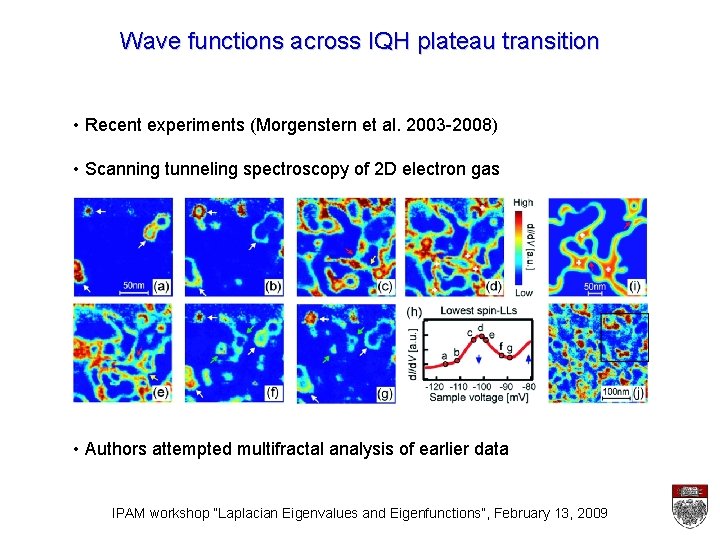
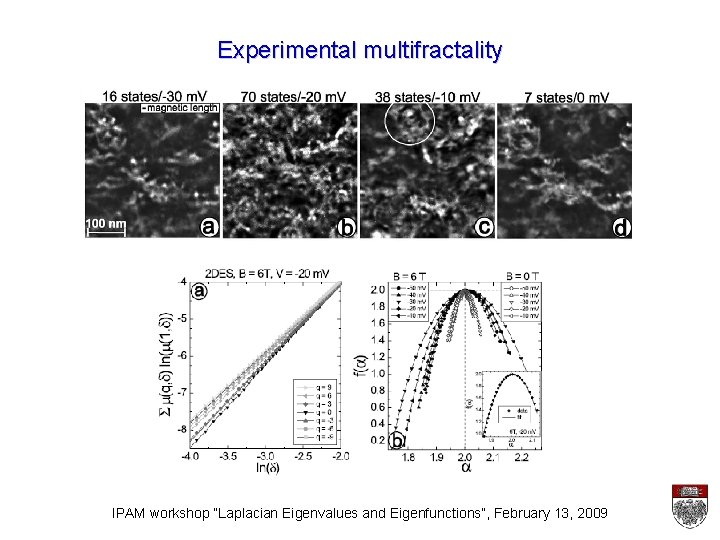
Wave functions across IQH plateau transition • Recent experiments (Morgenstern et al. 2003 -2008) • Scanning tunneling spectroscopy of 2 D electron gas • Authors attempted multifractal analysis of earlier data IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Experimental multifractality IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009

Conclusions • Scaling of critical wave functions contains a lot of useful information • Multifractal spectrum of a whole system is crucially modified by presence of boundaries (should be property of multifractals in general) • Boundary and corner multifractal spectra provide direct numerical evidence of conformal invariance at 2 D Anderson transitions • Multifractal spectrum at the IQH plateau transition is not parabolic, ruling out existing theoretical proposals • Stochastic geometry (conformal restriction): a new approach to quantum Hall transitions (and other Anderson transitions) IPAM workshop “Laplacian Eigenvalues and Eigenfunctions”, February 13, 2009