Analyse des donnes Plan Lien entre les statistiques

Analyse des données

Plan • Lien entre les statistiques et l’analyse des données • Propagation des erreurs • Ajustement de fonctions

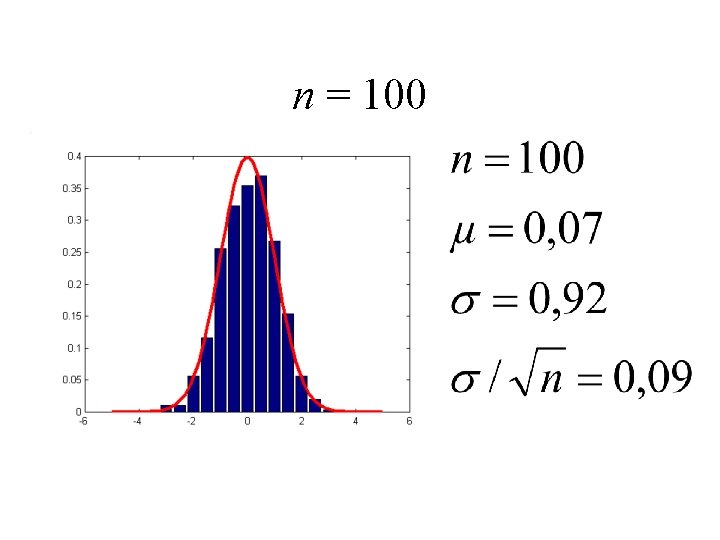
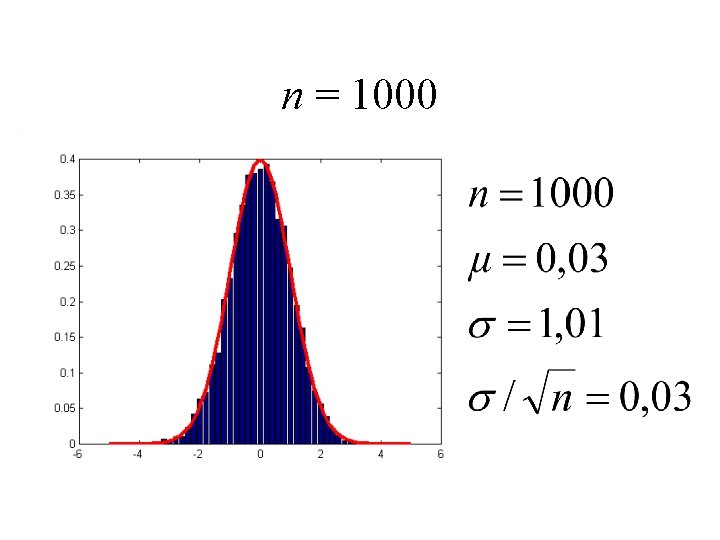
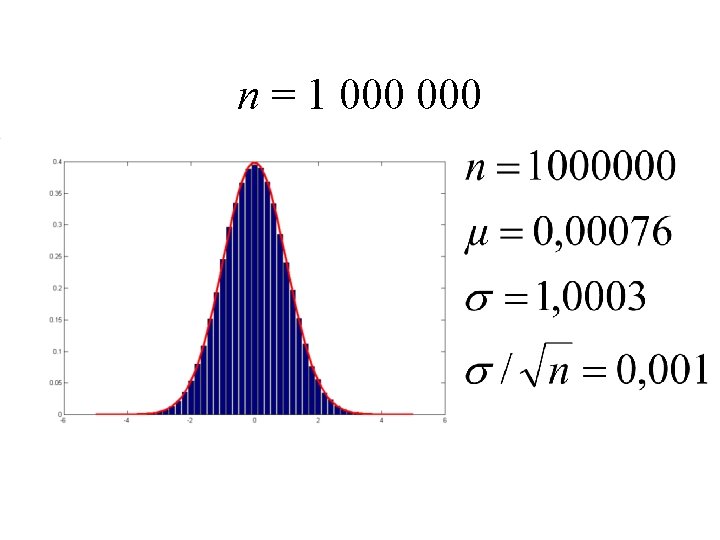
Échantillon vs population • Une mesure échantillonne une population • La distribution de l’échantillon approxime celle de la population • La précision sur les estimations augmente avec la taille de l’échantillon N

Exemple de comptage

n = 100

n = 1000

n = 1 000

Précision sur la moyenne • L’estimation de la moyenne s’affine avec N Population Échantillon

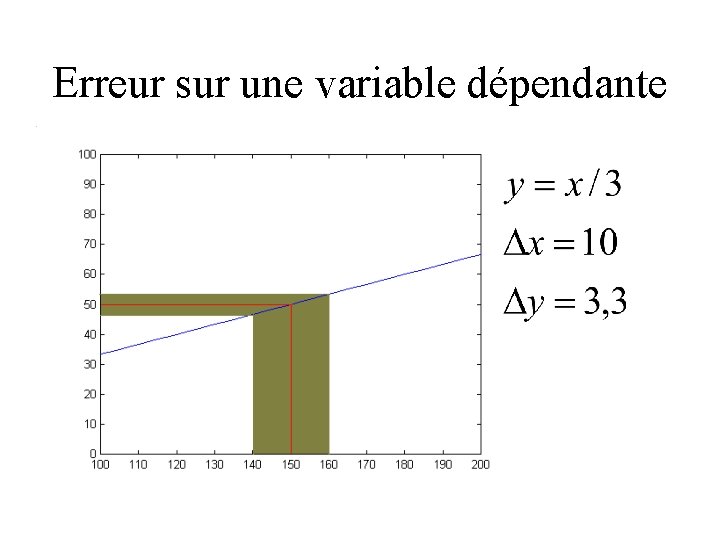
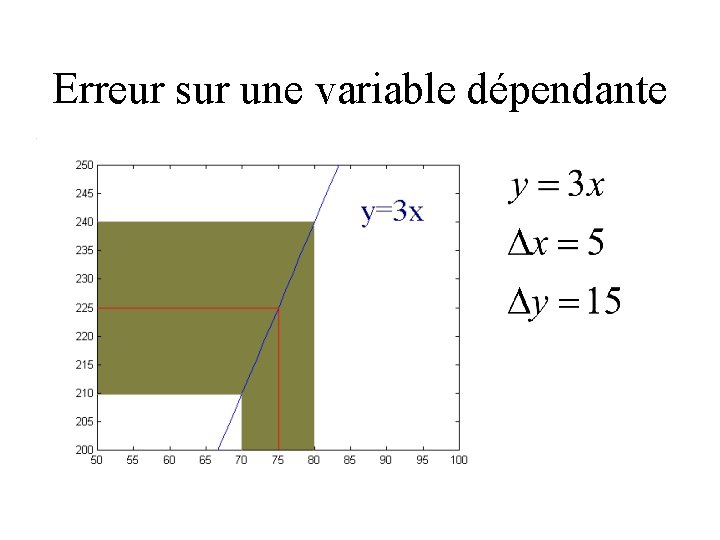
Erreur sur une variable dépendante

Erreur sur une variable dépendante

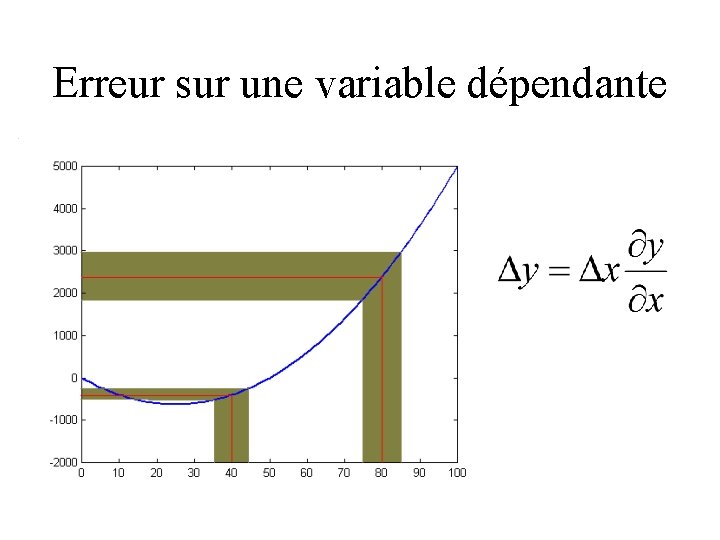
Erreur sur une variable dépendante

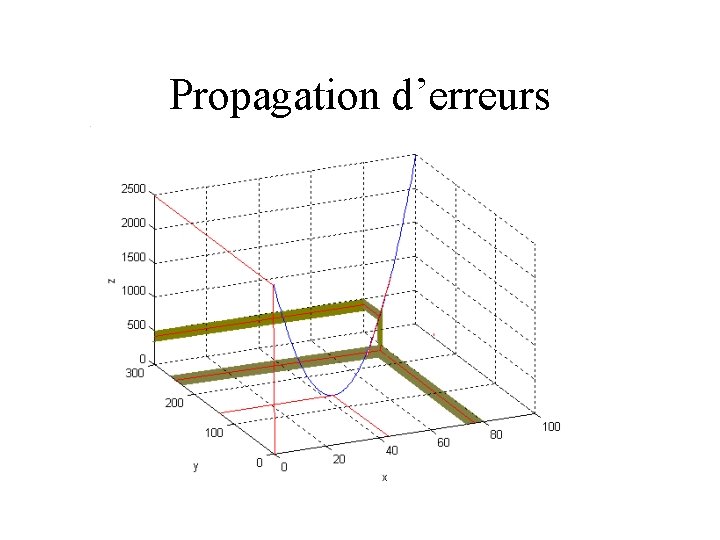
Propagation d’erreurs

Propagation d’erreurs

Propagation d’erreurs • x et y sont des variables indépendantes • Et Dx et Dy sont des erreurs indépendantes • Leurs effets s’additionnent quadratiquement

Propagation d’erreur pour des incertitudes indépendantes

Propagation d’erreurs (sans corrélations)

Moyenne pondérée • Plusieurs mesures de x (x 1, x 2, . . . xi, , . . . xn) • Différentes précisions (d 1, d 2, . . . di, , . . . dn) • On cherche la meilleure évaluation de la moyenne µ • Les mesures précises doivent contribuer davantage

Moyenne pondérée Si tous les si sont égaux,

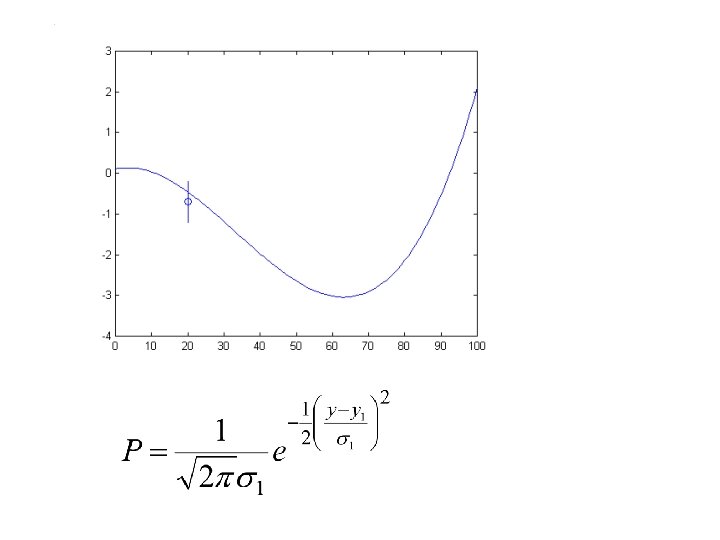
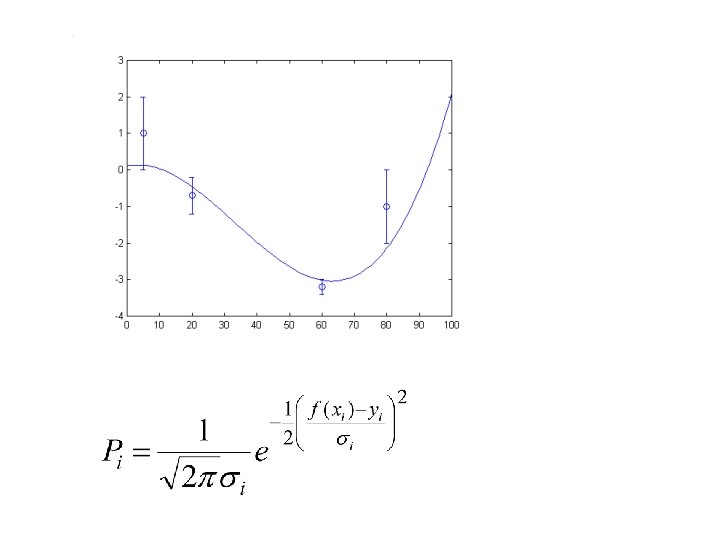
Ajustement de courbes • Soit f(x) une fonction physique • On fait une mesure de f(x) en x = x 1 • On cherche la probabilité que la mesure soit bonne

• La probabilité totale est

• La valeur de P ou de c 2 nous dit si les mesures représentent bien la théorie

Ajustement • En général, la situation est inversée • On ne connaît pas f(x) • Mais on connaît (ou on essaye) une forme – droite – polynôme – fonction arbitraire

Ajustement • On cherche les ai qui maximisent P – Vraisemblance maximale – Maximum likelihood • Ou qui minimisent c 2 – Moindres carrés

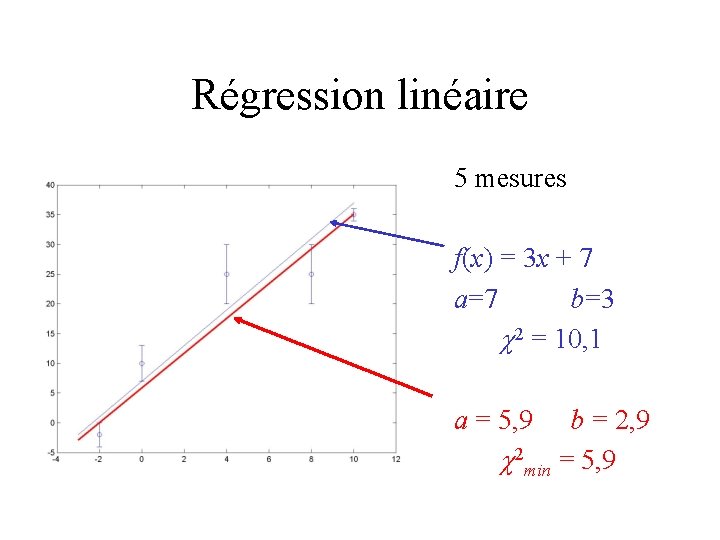
Régression linéaire • On veut passer la meilleure droite à travers n points expérimentaux

Régression linéaire • On cherche a et b qui minimisent c 2 • 2 équations, 2 inconnus (a et b)

Régression linéaire

Incertitudes égales (votre calculatrice)

Régression linéaire • 5 mesures • f(x) = 3 x + 7 • a=7 b=3 c 2 = 10, 1 • a = 5, 9 b = 2, 9 c 2 min = 5, 9

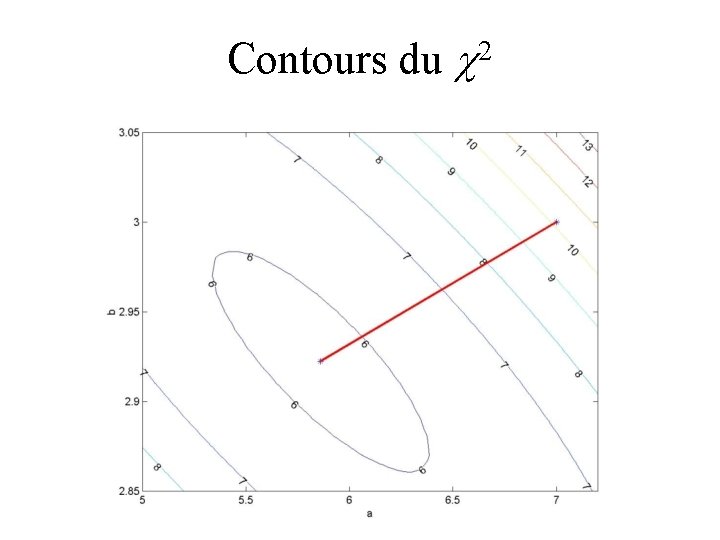
Contours du c 2

Incertitude sur les paramètres • a et b dépendent des yi • sa et sb dépendent des si • On applique la règle de propagation

Incertitude sur les paramètres

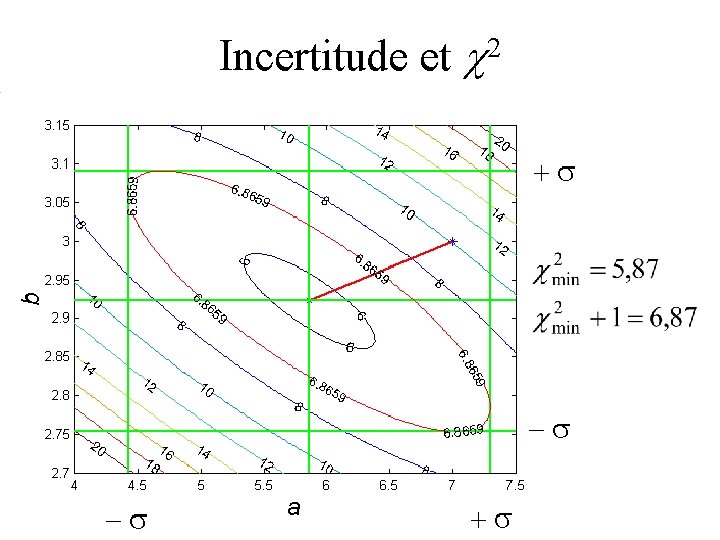
Incertitude et c 2

Incertitude et c 2 • La régression linéaire trouve le minimum du c 2 • Un écart-type sur les paramètres correspond à une augmentation de 1 du c 2. Pourquoi ? • Les courbes de niveau indiquent la corrélation entre les paramètres

Incertitude et c 2 Gaussienne d’écart-type = 1 L’incertitude représente une variation de 1 du c 2

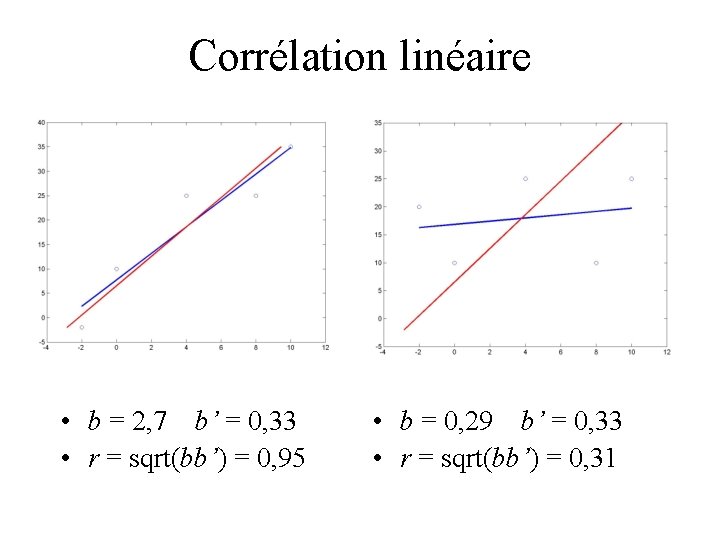
Corrélation linéaire • On peut toujours passer une droite par des points • Mais ces points peuvent-ils être décrits par une droite ? • Le coefficient de corrélation linéaire r nous donne la réponse

Corrélation linéaire • b = 2, 7 b’ = 0, 33 • r = sqrt(bb’) = 0, 95 • b = 0, 29 b’ = 0, 33 • r = sqrt(bb’) = 0, 31

Élimination de données suspectes Critère de Chauvenet (pp. 154 -156) • • Soit 5 mesures : 38 35 39 39 34 18 Faut-il rejeter la dernière valeur ? Si on peut expliquer notre erreur, oui. Sinon, il faut réfléchir <x> = 34 s=8 Si on enlève, on a <x> = 37 La valeur de 18 s’écarte de 2 s de la moyenne

• Ceci n’est jamais impossible et devrait se produire ~ 1 fois sur 20 • Mais on n’a que 6 données • On attend donc ~ 0, 3 données de ce type et on l’écarte • Critère de Chauvenet • On écarte si

Attention à l’auto-censure • Expérience de Millikan • e = 1, 592 × 10 -19 C • e = 1, 602 × 10 -19 C • Temps de vie du muon