4 Mtodos matemticos Funciones Discretas Para estudiar la




















- Slides: 21

4. Métodos matemáticos

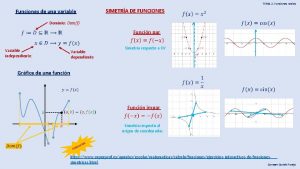
Funciones Discretas • Para estudiar la eficiencia de los algoritmos, generalmente usamos funciones discretas, que miden cantidades tales tiempo de ejecución, memoria utilizada, etc. • Estas funciones son discretas porque dependen del tamaño del problema (n). Por ejemplo, n podría representar el número de elementos a ordenar. • Notación: f (n) o bien fn , representa al tiempo, por eso también se usa T(n) o Tn

Notación O • Se dice que una función f (n) es O(g(n)) si existe una constante c > 0 y un n 0 >= 0 tal que para todo n >= n 0 se tiene que f (n) <= cg(n). (cota superior de un algoritmo) • Se dice que una función f (n) es Ω(g(n)) si existe una constante c > 0 y un n 0 >= 0 tal que para todo n >= n 0 se tiene que f (n) >= cg(n). (cota inferior) • Se dice que una función f (n) es Θ (g(n)) si f (n) = O(g(n)) y f (n) = Ω(g(n)).

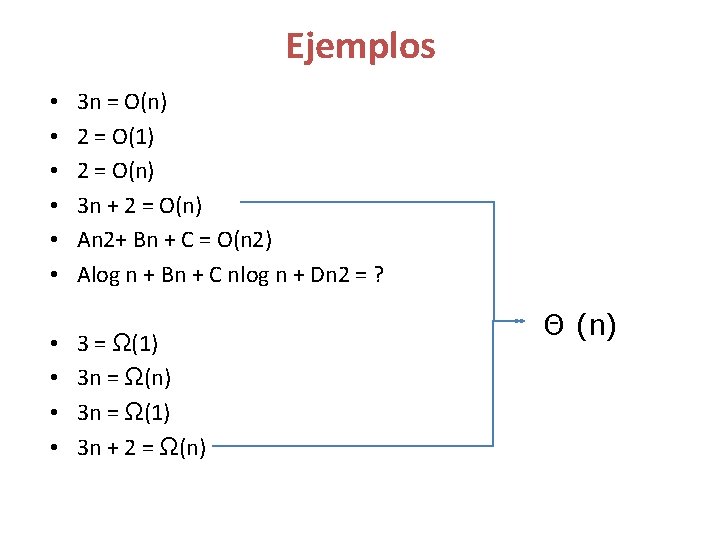
Ejemplos • • • 3 n = O(n) 2 = O(1) 2 = O(n) 3 n + 2 = O(n) An 2+ Bn + C = O(n 2) Alog n + Bn + C nlog n + Dn 2 = ? 3 = Ω(1) 3 n = Ω(n) 3 n = Ω(1) 3 n + 2 = Ω(n) Θ (n)

Ecuaciones de Recurrencia • Son ecuaciones en que el valor de la función para un n dado se obtiene en función de valores anteriores. • Esto permite calcular el valor de la función para cualquier n, a partir de condiciones de borde (o condiciones iniciales) • Ejemplo: Torres de Hanoi an = 2 an-1 + 1 a 0 = 0 • Ejemplo: Fibonacci fn = fn-1 + fn-2 f 0 = 0 f 1 = 1

Ecuaciones de Primer Orden • Consideremos una ecuación de la forma an = ban-1 + cn • donde b es una constante y cn es una función conocida. • Como precalentamiento, consideremos el caso b = 1: an = an-1 + cn • Esto se puede poner en la forma an - an-1 = cn • Sumando a ambos lados, queda una suma telescópica: • an = a 0 + Σ c k 1<=k<=n

Ecuaciones de Primer Orden: (cont. ) • Para resolver el caso general: an = ban-1 + cn • dividamos ambos lados por el “factor sumante” bn: an/bn = an-1/bn-1 +cn/bn • Si definimos An = an /bn, Cn = cn=bn, queda una ecuación que ya sabemos resolver: An = An-1 + Cn con solución An = A 0 + Σck 1<=k<=n • y finalmente an = a 0 bn + Σckbn-k 1<=k<=n

Ejemplo: Torres de Hanoi • El número de movimientos de discos está dado por la ecuación an = 2 an-1 + 1 a 0 = 0 • De acuerdo a lo anterior, la solución es an = Σ 2 n-k = Σ 2 k 1<=k<=n • Lo que significa an = 2 n-1 0<=k<=n-1

Propuesto • Generalizar este método para resolver ecuaciones de la forma an = bnan-1 + cn • donde bn y cn son funciones conocidas.

Ecuaciones Lineales con coef. Const. • Ejemplo: Fibonacci fn = fn-1 + fn-2 f 0 = 0 f 1 = 1 • Este tipo de ecuaciones tienen soluciones exponenciales, de la forma fn = λn: fn = fn-1 + fn-2 λn = λn-1 + λn-2 • Dividiendo ambos lados por λn-2 obtenemos la ecuación característica λ 2 - λ + 1 = 0 • cuyas raíces son Ф 1= (1+ sqrt(5))/2 ≈ 1. 618 Ф 2= (1 - sqrt(5))/2 ≈ 0. 618

Ecuaciones Lineales con coef. Const. • La solución general se obtiene como una combinación lineal de estas soluciones: fn = A Ф 1 n + B Ф 2 n • La condición inicial f 0 = 0 implica que B = -A, esto es, fn = A(Ф 1 n - Ф 2 n) • y la condición f 1 = 1 implica que A(Ф 1 - Ф 2) = A sqrt(5) = 1 • con lo cual obtenemos finalmente la fórmula de los números de Fibonacci: fn =(1 /sqrt(5)) (Ф 1 n - Ф 2 n) • Nótese que Ф 2 n tiende a 0 cuando n tiende a infinito, de modo que fn = Θ (n)

Teorema Maestro (div. para reinar) • Consideremos la ecuación de la forma T(n) = p. T(n/q) + Kn • Supongamos que n es una potencia de q, digamos n = q k Entonces T(q k ) = p. T(q k -1 ) + Kq k • Y si definimos a k = T(q k ) tenemos la ecuación: a k = pa k -1 + Kq k • La cual tiene solución a k = a 0 p k + K Σqjpk-j (ver al principio) 1<=j<=n

Teorema Maestro (cont. ) • Como k = log q n, tenemos T(n) = T(1)plog q n + Kplog q n Σ(q/p)j 1<=j<=log q n • Y observamos que plog q n = (qlog q p) log q n =(qlog q n) log q p =(n) log q p • Por lo tanto: T(n) = (n) log q p (T(1) + K Σ(q/p)j ) 1<=j<=log q n

Teorema Maestro: caso p < q T(n) = p. T(n/q) + Kn

Teorema Maestro: caso p = q T(n) = p. T(n/q) + Kn

Teorema Maestro: caso p > q T(n) = p. T(n/q) + Kn

Dividir para Reinar Este es un método de diseño de algoritmos que se basa en subdividir el problema en sub-problemas, resolverlos recursivamente, y luego combinar las soluciones de los sub-problemas para construir la solución del problema original. Ejemplo: Multiplicación de Polinomios. Supongamos que tenemos dos polinomios con n coeficientes, o sea, de grado n-1: A(x) = a 0+a 1*x+. . . +an-1*xn-1 B(x) = b 0+b 1*x+. . . +bn-1*xn-1 representados por arreglos a[0], . . , a[n-1] y b[0], . . , b[n-1]. Queremos calcular los coeficientes del polinomio C(x) tal que C(x) = A(x)*B(x).

Solulción Un algoritmo simple para calcular esto es: // Multiplicación de polinomios for( k=0; k<=2*n-2; ++k ) c[k] = 0; for( i=0; i<n; ++i) for( j=0; j<n; ++j) c[i+j] += a[i]*b[j]; Evidentemente, este algoritmo requiere tiempo O(n 2). ¿Se puede hacer más rápido?

Dividir-componer Supongamos que n es par, y dividamos los polinomios en dos partes. Por ejemplo, si A(x) = 2 + 3*x - 6*x 2 + x 3 entonces se puede reescribir como A(x) = (2+3*x) + (-6+x)*x 2 y en general A(x) = A'(x) + A"(x) * xn/2 B(x) = B'(x) + B"(x) * xn/2 Entonces C = (A' + A"*xn/2) * (B' + B"*xn/2) = A'*B' + (A'*B" + A"*B') * xn/2 + A"*B" * xn

Dividir-componer (cont. ) C = (A' + A"*xn/2) * (B' + B"*xn/2) = A'*B' + (A'*B" + A"*B') * xn/2 + A"*B" * xn Esto se puede implementar con 4 multiplicaciones recursivas, cada una involucrando polinomios de la mitad del tamaño que el polinomio original. T(n) = 4*T(n/2) + K*n donde K es alguna constante cuyo valor exacto no es importante. Por lo tanto la solución del problema planteado (p=4, q=2) es T(n) = O(nlog 2 4) = O(n 2) lo cual no mejora al algoritmo visto inicialmente.

Dividir-componer (cont. ) Pero. . . hay una forma más eficiente de calcular C(x). Si renombramos : D = (A'+A") * (B'+B") E = A'*B‘ F = A"*B" entonces C = E + (D-E-F)*xn/2 + F*xn Lo cual utiliza sólo 3 multiplicaciones recursivas, en lugar de 4. Esto implica que T(n) = O(nlog 2 3) = O(n 1. 59)
 Solucionar
Solucionar Variables ordinales
Variables ordinales Variable aleatoria continua normal
Variable aleatoria continua normal Variables cualitativas
Variables cualitativas Destreza motriz
Destreza motriz Señales discretas y continuas
Señales discretas y continuas Preorden inorden postorden
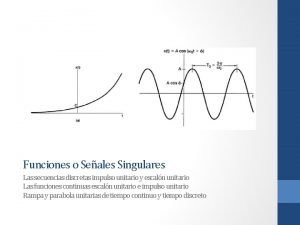
Preorden inorden postorden Funciones singulares escalón impulso y rampa unitaria
Funciones singulares escalón impulso y rampa unitaria Que representa
Que representa Serie de fourier exponencial
Serie de fourier exponencial Formula de la distribucion hipergeometrica
Formula de la distribucion hipergeometrica Estructuras discretas pucp
Estructuras discretas pucp Mtodos
Mtodos Mtodos
Mtodos Mtodos
Mtodos Mtodos
Mtodos Mtodos
Mtodos Gynefix diu
Gynefix diu Mtodos
Mtodos Mtodos
Mtodos Método del ritmo para no quedar embarazada
Método del ritmo para no quedar embarazada Mtodos
Mtodos