2 Static Games with Complete Information 2 2




























































- Slides: 79

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies ã ã ã Until now, we dealt with games with several strategies with dominance, minimax, BRA and cellby-cell check. However, these methods are not suitable or applicable to the games with infinite or many strategies. 보상표를 그릴 수 없음 Ex) price decision games. Infinite number of price levels. Thus, new algorithm is needed to find equilibria. Also, some criticisms and advocacy of NE will be discussed. 1/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition We will take the BRA method or in other words, the basic idea of BRA per se (in itself). ã That is, we will use the best response function (or curve) that maximizes players’ payoffs. The intersection(s) of the best response functions of the players will be the NE (동시에 최적반응이므로 교차점). ã Ex) There are two Gimbab(김밥) restaurants in the neighborhood, ‘Gimbab Daetongryung(President) (D)’ and ‘Gimbab Nara(Nation). ’ The two produce the same quality Gimbab. Price is the only strategy for both. The two restaurants’ goals are to maximize their profits. Both do not know the competitor’s price until they announce their prices on the window simultaneously. They have to decide their own prices in these conditions. SM strategy game. ã 2/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) D’s price is represented as Pd, N’s price is Pn. Units are 100 KRW. ã The unit cost of Gimbab production is 8 for both. ã Through market research, the quantities (Qd, Qn ; unit is 100 Gimbab) sold according to the price are as follows: ã Qd = 44 – 2*Pd + Pn Qn = 44 – 2*Pn + Pd *Different from usual demand function because the demand for D’s Gimbab not only depends on D’s own price but also N’s price(대체재 가격). That is, if N increase its price(Pn↑), D’s Gimbab sells more. (Qd↑) If N increases price 1 unit (100 KRW), 1 unit(100 Gimbab) of D’s Gimbab will be sold more. 3/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) Also, if D raises its price 1 unit (100 KRW), its sales will decrease 2 units(200 Gimbab). ã Further more, for example, if N raises its price by 1 unit, N’s sales decreases by 2 units (예를 들어, 나라 의 가격 인상으로, 나라의 고객 100명은 대통령가서 100개 사먹으므로 나라의 판매량 1단위(100개) 줄고, 다른 1단위(100개)는 나라 김밥에 대한 수요가 사라짐. 반대도 마찬가지). ã Qd = 44 – 2*Pd + Pn Qn = 44 – 2*Pn + Pd *Profit? Profit = sales – cost=price*quantity-unit cost*quantity =(price-unit cost)*quantity 4/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Profits of D and N: Profitd = (Pd – 8)*Qd=(Pd – 8)*(44 – 2*Pd + Pn) Profitn = (Pn – 8)*Qn=(Pn – 8)*(44 – 2*Pn + Pd) Profit maximizing price can be derived through differentiation. Later. ã Before that, let’s assume as many as possible (to mimic continuous strategy) discrete strategies and set up the payoff table to see how fast it gets complicated if we try to solve the game using the old method of pay-off table. ã 5/63

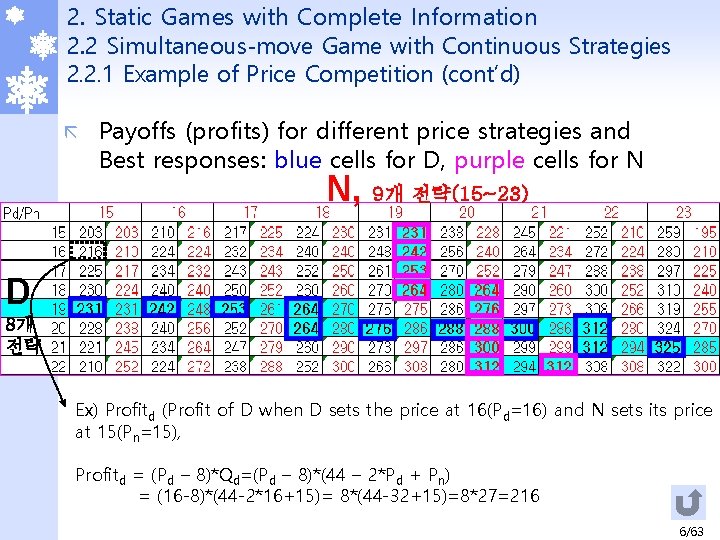
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Payoffs (profits) for different price strategies and Best responses: blue cells for D, purple cells for N N, 9개 전략(15~23) D 8개 전략 Ex) Profitd (Profit of D when D sets the price at 16(Pd=16) and N sets its price at 15(Pn=15), Profitd = (Pd – 8)*Qd=(Pd – 8)*(44 – 2*Pd + Pn) = (16 -8)*(44 -2*16+15)= 8*(44 -32+15)=8*27=216 6/63

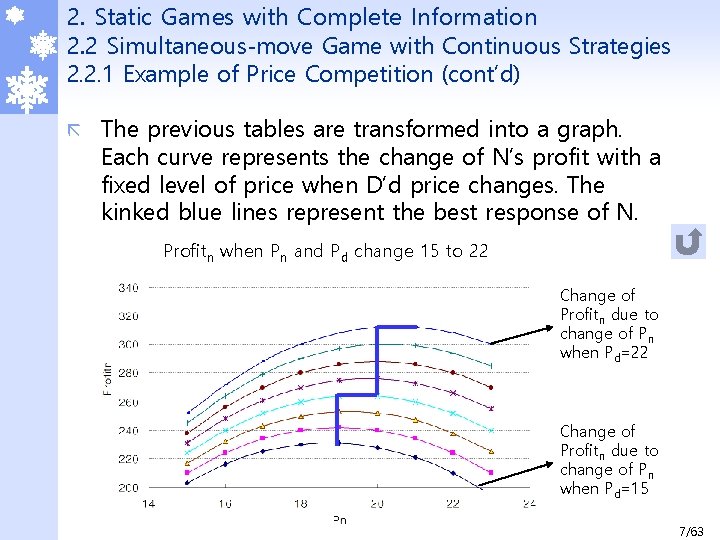
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã The previous tables are transformed into a graph. Each curve represents the change of N’s profit with a fixed level of price when D’d price changes. The kinked blue lines represent the best response of N. Profitn when Pn and Pd change 15 to 22 Change of Profitn due to change of Pn when Pd=15 7/63

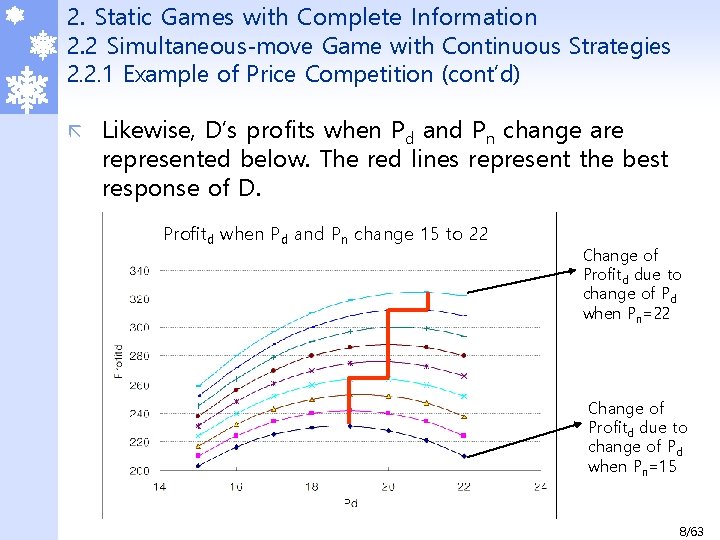
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Likewise, D’s profits when Pd and Pn change are represented below. The red lines represent the best response of D. Profitd when Pd and Pn change 15 to 22 Change of Profitd due to change of Pd when Pn=15 8/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã In a 3 D graph? More complicated. Thus, we will use algebra. (14, 14) 14 9/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã The best-response function of D when the price of N is given can be presented as follows; Controllable by D Not controllable by D Profit of D: Profitd = (Pd – 8)*Qd=(Pd – 8)*(44 – 2*Pd + Pn) The best response of D? Set the price of D so that it maximizes D’s profit!! *D는 자기 자신의 가격(Pd)만 바꿀 수 있으며, 상대방 가격(Pn)은 주어 지므로 못 바꿈 Pn 이 주어졌을 때 Pd 를 바꾸면서 이윤이 최대가 되 도록 하는 규칙을 찾아야 함 미분(微分; differentiation)!! 10/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) y ã Differentiation=take derivative=미분 Slope= -2, at x=1 2 1 1 2^(1/2) x y = 2 - x 2 ã Or more advanced way is to use the formula 11/63

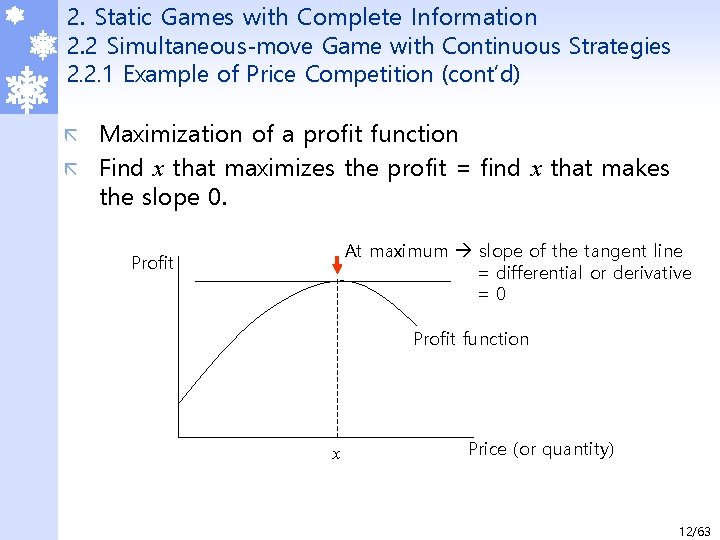
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) Maximization of a profit function ã Find x that maximizes the profit = find x that makes the slope 0. ã At maximum slope of the tangent line = differential or derivative =0 Profit function x Price (or quantity) 12/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Thus, the max. of D’s profit can be derived by differentiating Profitd w. r. t. Pd. At the max. , the differential should be ‘ 0. ’ Profit of D = πd = (P d – 8)*(44 – 2*P d + Pn) That is, D’s best response price (Pd*) depends on Pn. Pd* =1/4 Pn + 15 ã If Pn=16, Pd* = ¼ *16 + 15 = 19 ã Confirm 13/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Likewise, the max. of N’s profit can be derived by differentiating Profitn w. r. t. Pn. At the max. , the differential should be also ‘ 0. ’ That is, N’s best-response(BR) price (Pn*) depends on Pd Pn* =1/4 Pd + 15 ã If Pd=16, Pn* = ¼ *16 + 15 = 19 ã Confirm 14/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Summing up, D and N’s BR function(line or curve)? *D’s best price responses to N’s price. *N’s best price responses to D’s price. ã Remind that N’s BR price that maximizes N’s profit is 19 when D sets its price at 16. ã Doesn’t N need to decrease its price lower than 16 to increase the sales and to meet the competition? NO. Check the payoff table. Ex) If Pd=16 and Pn=19, Profit n = 242 If Pd=16 and Pn=15, Profit n = 210 15/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) Why so? Why does N get higher profit by setting N’s price higher at 19 than D’s price of 16? ã If N sets the price higher, the quantity sold will decrease but the sales (=price*quantity) will increase due to higher price. ã That is, the rate of decrease in quantity sold is smaller than the rate of increase in price sold. ã To be more precise, the rate of increased net unit profit (=unit price-unit cost) is bigger than the rate of decreased unit quantity. Because the unit cost is fixed in this example, the rate of increased net profit is equal to the rate of increased price. ã 16/63

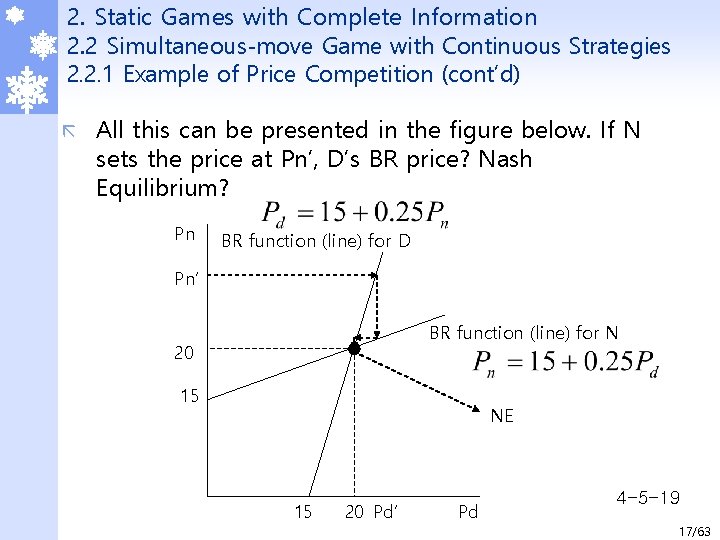
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã All this can be presented in the figure below. If N sets the price at Pn’, D’s BR price? Nash Equilibrium? Pn BR function (line) for D Pn’ BR function (line) for N 20 15 NE 15 20 Pd’ Pd 4 -5 -19 17/63

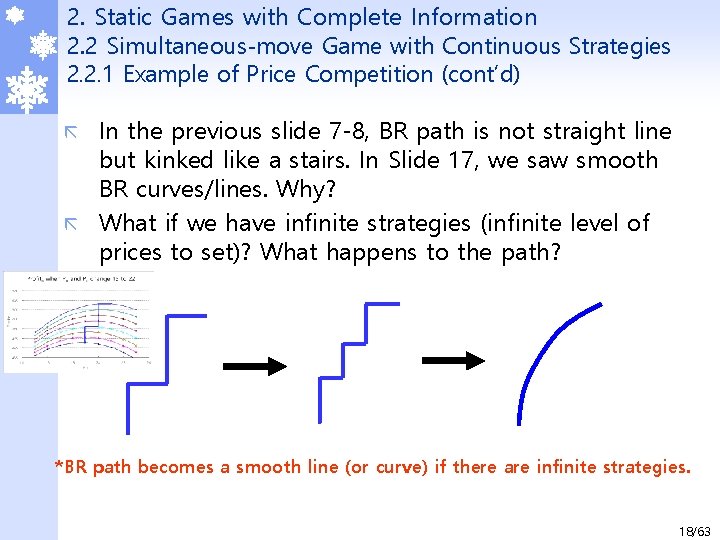
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) In the previous slide 7 -8, BR path is not straight line but kinked like a stairs. In Slide 17, we saw smooth BR curves/lines. Why? ã What if we have infinite strategies (infinite level of prices to set)? What happens to the path? ã *BR path becomes a smooth line (or curve) if there are infinite strategies. 18/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã Or if we solve the two equations by substitution, Then, P*d=20. Then if P*d=20 is plugged in the Qd = 44 – 2*Pd + Pn previous equation, we get P*n=20. Qn = 44 – 2*Pn + Pd ã Thus, at NE, the two will set the prices both at 20 (2, 000 KRW) and each will sell 24 units (2, 400 Gimbab). ã In this case, the profit for each will be Profit = (P – 8)*Q=(20 -8)*24=288 (unit=10, 000 KRW) ã Confirm 19/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) In the BR functions, if the competitor increases price by 1(100원), I have to increase a fraction (0. 25, 25원 ) to be optimal. ã That is, if the competitor increases the price, I have to increase the price less than the competitor to induce the consumers to buy my Gimbab more. ã In this case, my profit maximizing price increase is 0. 25(25원; ¼ or 25% of competitor’s price increase). If I increases more or less than that, the competitor’s profit will increase and I can’t maximize my profit. ã What if the competitor decrease by 1? Decrease price by a fraction of 0. 25. ã 20/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) Qd = 44 – 2*Pd + Pn Qn = 44 – 2*Pn + Pd Is there any other way to increase profit further? NO. ã Let’s say that both could agree to increase the prices simultaneously to 24 through collusion. ã If they could do this; Sales = 44 -2*24+24 = 20. (판매량은 24에서 20으로 감소, 경기침체? ) Profit = (P – 8)*Q=(24 -8)*20=16*20=320 (288에서 320으 ã 로 순수익증가, 가능? ) Similar to Prisoners’ Dilemma. But now strategies are continuous. ã Will this collusion work? Same as in the Prisoners’ Dilemma, NO. Does one (D or N) have an incentive to break the price collusion when the other sets the price at 24? YES! The collusion will not hold. Why? (Next) ã 21/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) If N sets the price at 24, D will set the price at 21 to maximize the profit. Why? 15+0. 25*24=21 (the profit of D in this case is 338. This is bigger than 320 when D keeps the promise. So cheat! ã Then, in reaction to D’s price reduction, N will again set the price at 20. 25 (N’s BR price = 15+0. 25*21=20. 25). ã Then, D again sets the price at 20. 0625 (= 15+0. 25*20. 25=20. 0625) ã And so on… Then we have the next figure. ã 22/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã When this price adjustment processes are repeated, the near NE will be reached in the mere 2 nd round of the game. Price Adjustment Process by BR Price of N Price of D Rounds N’s price D’s price 100 KRW D cheats first. 23/63

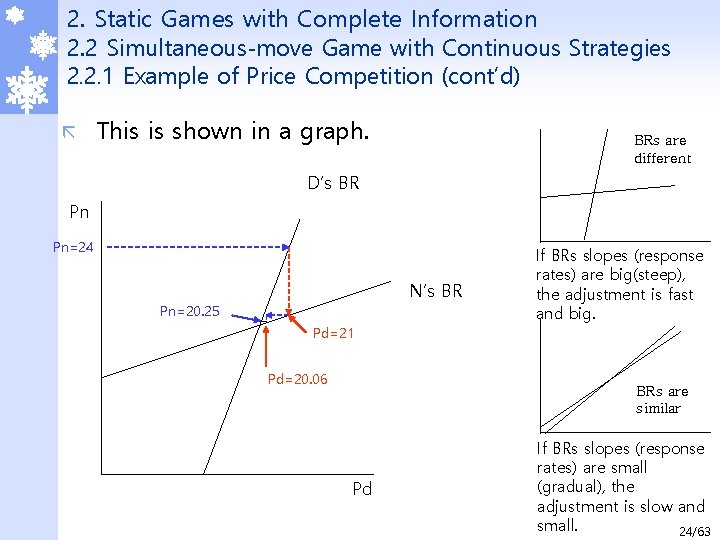
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã This is shown in a graph. BRs are different D’s BR Pn Pn=24 N’s BR Pn=20. 25 If BRs slopes (response rates) are big(steep), the adjustment is fast and big. Pd=21 Pd=20. 06 BRs are similar Pd If BRs slopes (response rates) are small (gradual), the adjustment is slow and small. 24/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã ã ã If D and N are very close friends or relatives so that the collusion are expected to work(binding agreement), they need to find the profit maximizing level of collusive price. What is the price that leads to the highest profit D and N can achieve through collusion? Collusion(가격단합) Same prices(Pd=Pn=P). Thus, N’s Profit=D’s Profit=(P-8)*(44 -2 P+P)=(P-8)(44 -P) should be maximized. Differentiate the profit w. r. t. P and set the slope (differential) = 0. (1)(44 -P)+(P-8)(-1)=-2 P+52=0 P*=26, Q*=18 That is, if both set the price at 26, the profits of the both will be maximized to 324. 김밥사먹는 사람 줄 어들고… 경기침체(판매량 24 18), 인플레(가격 20 26)… ‘단합’은 전체경제에 나쁨 25/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 1 Example of Price Competition (cont’d) ã ã ã This price collusion is called the ‘Cartel’ and regarded as illegal. So you can’t do this. Collusion not necessarily leads to price increase. It leads to price increase when the products are substitutes because one’s price reduction leads to sales reduction of another. If the products are complements, one’s price reduction increases not only one’s sales but also another’s sales, which is mutually beneficial. Thus, if they are complementary goods, collusion may lead to price reduction. 전체경제에 도움 OK Ex) Intel chips and Microsoft OS 26/63

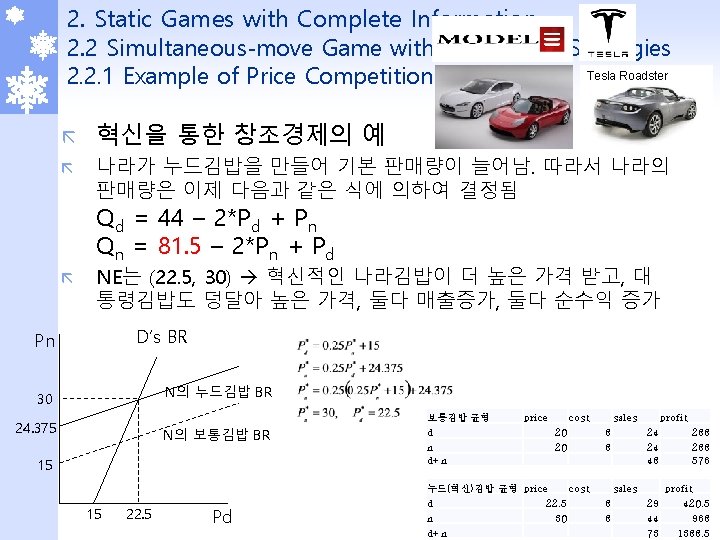
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies Tesla Roadster 2. 2. 1 Example of Price Competition (cont’d) ã ã 혁신을 통한 창조경제의 예 나라가 누드김밥을 만들어 기본 판매량이 늘어남. 따라서 나라의 판매량은 이제 다음과 같은 식에 의하여 결정됨 Qd = 44 – 2*Pd + Pn Qn = 81. 5 – 2*Pn + Pd ã NE는 (22. 5, 30) 혁신적인 나라김밥이 더 높은 가격 받고, 대 통령김밥도 덩달아 높은 가격, 둘다 매출증가, 둘다 순수익 증가 D’s BR Pn N의 누드김밥 BR 30 24. 375 N의 보통김밥 BR 15 15 22. 5 Pd 보통김밥 균형 d n d+n price cost 20 20 누드(혁신)김밥 균형 price cost d 22. 5 n 30 d+n sales 8 8 24 24 48 sales 8 8 profit 288 576 profit 29 420. 5 44 968 27/63 73 1388. 5

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function In the previous example of price competition, BR functions were linear (straight line). ã But BR functions are generally curves (non-linear). In the non-linear cases, a more sophisticated mathematics is needed. ã Consider an election game with two competitors. Each can earn more votes by advertising one’s advantages or another’s disadvantages(네거티브 전략). ã Also assume that 1) voters only rely on the advertisement and make their decision 2) votes depend on the amount of advertisement. ã 28/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) Two parties: Democrats (L; Left, progressive, 좌익(left wing)) and Republican (R; Right, conservative; 우익(right wing)). ã Election cost (billion KRW) : L x, R y ã L’s votes secured = x/(x + y) ã R’s votes secured = y/(x + y) ã *전체 광고비 중 L의 광고비 비중에 따라 득표) *전체 광고비 중 R의 광고비 비중에 따라 득표) Payoff for L = x/(x + y) - x ã Payoff for R = y/(x + y) - y ã Ex) x=0. 3(3억원), y=0. 6(6억원); Payoff for L party= 0. 3/0. 9 -0. 3=0. 33 -0. 3 = 0. 03 (30 million votes) Payoff for R party= 0. 6/0. 9 -0. 6=0. 67 -0. 6 = 0. 07 (70 million votes) 29/63

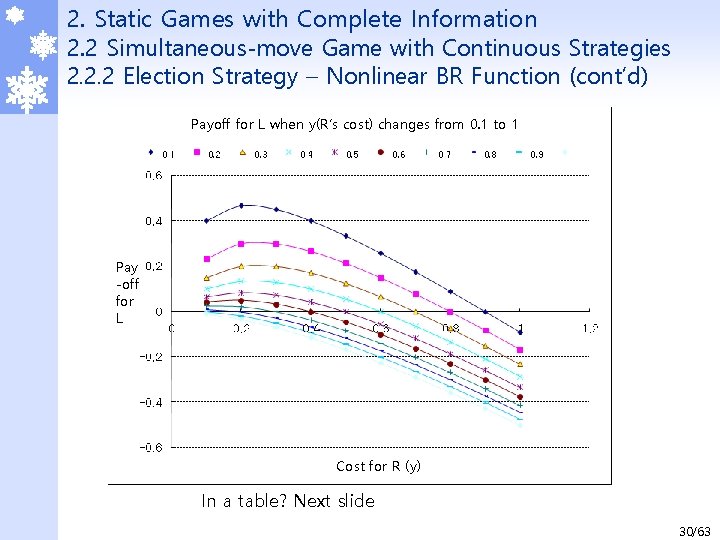
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) Payoff for L when y(R’s cost) changes from 0. 1 to 1 Pay -off for L Cost for R (y) In a table? Next slide 30/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã We could make the strategy discrete and try to find NE using payoff table as below. ã We may find two or three NEs. Will we find more than 2 NEs if we make the strategy finer? We don’t know. very inaccurate prediction Algebraic approach is more appropriate to find all possible NEs. 31/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã The payoff maximizing problem 4 -10 -19 32/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã The payoff maximizing condition using chain rule. f(y) g(y) 1·(x + y)-1 - 1 Chain rule Differentiation Rule for Product of functions Why set to 0 (zero)? 33/63

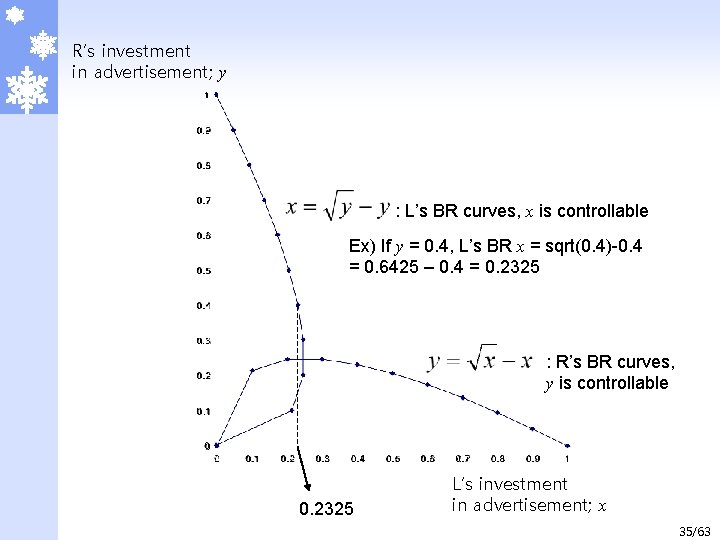
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã That is, R’s BR curve is as follows. ã Likewise, L’s BR curve is as follows. 34/63

R’s investment in advertisement; y : L’s BR curves, x is controllable Ex) If y = 0. 4, L’s BR x = sqrt(0. 4)-0. 4 = 0. 6425 – 0. 4 = 0. 2325 : R’s BR curves, y is controllable 0. 2325 L’s investment in advertisement; x 35/63

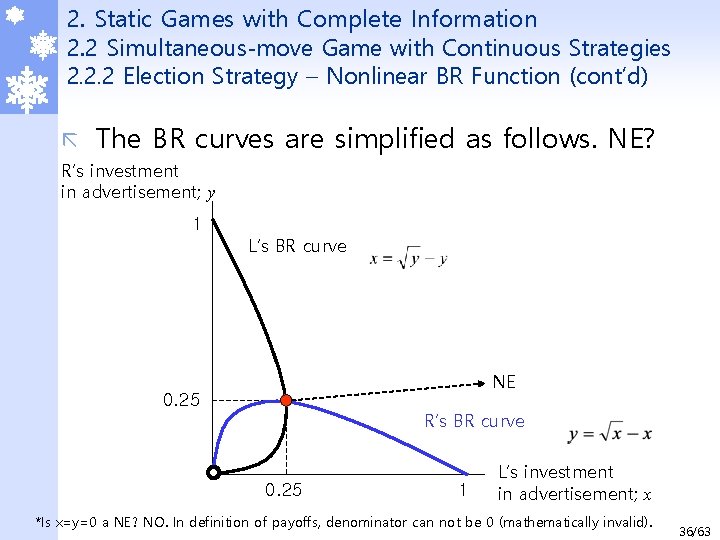
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã The BR curves are simplified as follows. NE? R’s investment in advertisement; y 1 L’s BR curve NE 0. 25 R’s BR curve 0. 25 1 L’s investment in advertisement; x *Is x=y=0 a NE? NO. In definition of payoffs, denominator can not be 0 (mathematically invalid). 36/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) If other party increases investment, one has to increase it faster as well. But after a certain point, one has to decrease it slower. ã That is, when other party’s investment is small, one can increase its payoff a lot by increasing its investment small Thus, increasing is better. ã But, if other party is investing heavily in advertisement, my increasing investment will not help much less efficient compared to my investment. ã In reality, however, political decision is made regardless of economic efficiency. Winning the election is the primary objective. If political utility can be monetized, it can be included in the model. ã 37/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã At the cross point of the two curves(x=y), each party’s payoffs are maximized. Where? At x=1/4, y=1/4. How do we know this? Replace x with y. 38/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã ã ã That is, each party will gain the most (highest votes) when they spend 0. 25 (billion KRW) NE!! Payoffs are 0. 25 for each as well (why? ). Again, this game is an example of PD. Why? They could collude and agree to decrease investments together, which will not change the votes earned. lead to less social/private cost. But they don’t. What if R is more efficient and decrease the investment but sustain the impact? Or R’s advertisement is twice more effective at the same cost? That is, L’s earned votes(payoff) is x/(x+y)-x, but R’s earned vote is 2 y/(x+y)-y? 39/63

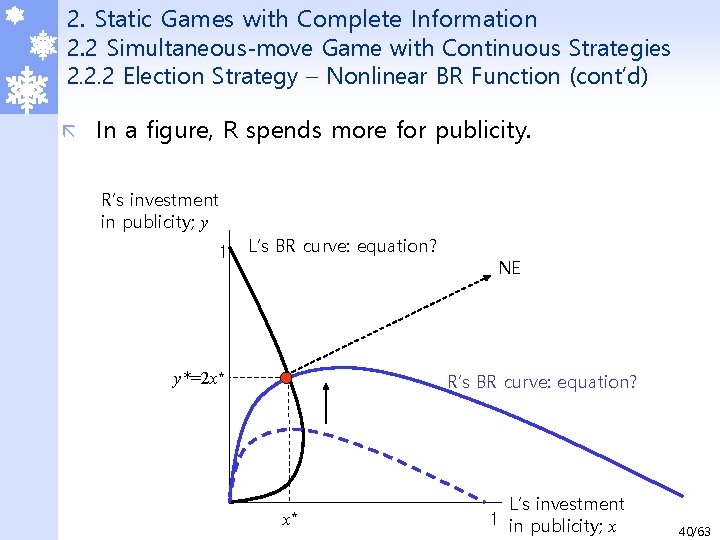
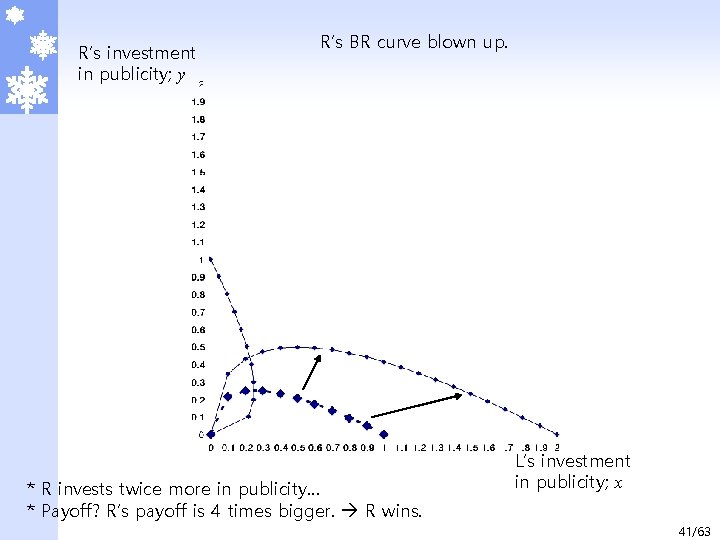
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã In a figure, R spends more for publicity. R’s investment in publicity; y 1 L’s BR curve: equation? NE R’s BR curve: equation? y*=2 x* x* L’s investment 1 in publicity; x 40/63

R’s investment in publicity; y R’s BR curve blown up. * R invests twice more in publicity… * Payoff? R’s payoff is 4 times bigger. R wins. L’s investment in publicity; x 41/63

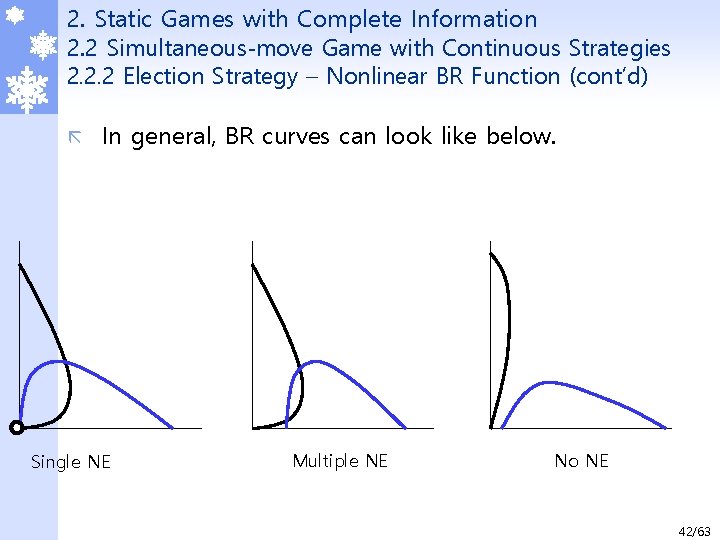
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 2 Election Strategy – Nonlinear BR Function (cont’d) ã In general, BR curves can look like below. Single NE Multiple NE No NE 42/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (1) Experiments in labs and classrooms Is the concept of NE practical when we have more variables and the games are more complex? ã In experimental or artificial environments, NE can lead to straightforward results. However, even in the experimental set-up, the game can lead to unexpected results due to lack of (players’) experiences. ã We can discard the early-unexpected results to get better results but learning can take a while. Thus, experiments have their limits. ã 43/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (1) Experiments in labs and classrooms (cont’d) It is reported that NE emerges as an equilibrium in relatively simple games with single NE. (Davis and Holt, 1993) ã However, in complex games with multiple NE, NE may not be selected as equilibria. ã In this respect, we will discuss the explanatory/coordination power of NE. ã 44/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (1) Experiments in labs and classrooms (cont’d) ã Selection of single eq. among multiple eq. ã If there is no focal point and/or no common cultural background, NE’s coordination power is decreased. (Schelling, 1960; Kreps, 1990). ã Ex) Select two persons from Seoul and Busan. Let them select a province from 8 provinces of Kyung-Gi, Kang. Won, Chung-Buk, Chung-Nam, Cheon-Buk, Cheon. Nam, Kyung-Buk, Kyung-Nam, simultaneously. If they select different provinces, they get reward. If they select the same province, they don’t get reward. NE? There are 56(=64 -8) NEs. Then, how do they select a province? ã Result: Most people divide/select geographically. For example, the people from Seoul tend to choose upper Taejeon provinces. The people from Busan tend to choose lower Taejeon provinces. What if the players are from Africa and have less knowledge of Korea? The chance of success decreases. Both would choose randomly. 45/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (1) Experiments in labs and classrooms (cont’d) Influence of Altruistic Behaviors ã In reality, NE is not selected due to altruistic consideration or fairness. ã For example, it is assumed that egoistic behaviors prevail in games. However, in reality, cooperative behaviors are frequently observed in prisoners’ dilemma games because of the possibility of repeated game, value system, etc. Money or selfishness are not what people always pursue… Ex) Behavioral Economics ã 46/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (1) Experiments in labs and classrooms (cont’d) ã ã ã Example of Convergence to NE by learning Setting : Pick up a paper and write your name. Choose any number between 0~100 and write it down. Submit it. Average the numbers submitted and pay 1000 KRW to the one who chose the closest to the half of the average. For example, 4 students submitted 0, 40, 60, 100. The avg. is 50. The half is 25. Thus, the one who chose 40 will get the money. Need 5 volunteers. Result? NE? on the other slide. 4 -12 -19 *Pareto Principle: 20%의 원인에서 80%의 결과가 초래 된다 80%의 매출이 20%의 손님으로 부터 온다, 80%의 토지를 20%가 소유, 47/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (1) Experiments in labs and classrooms (cont’d) ã ã ã Example of Convergence to NE by learning(cont’d) How to interpret the result? One can argue that if NE is not selected, the prediction power of NE is negligible and therefore, there is no theoretical implication. What if the game is repeated? We observed the result converge to NE very fast. That is, NE is achieved when people understand (or learn) that other would play NE strategies in reaction to my NE strategy. What if players are replaced each round and new players are not aware of NE? 48/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (2) Empirical Proofs ã ã ã Predictive Power of NE Approaches to explain the real situation with GT; international trades, industrial organization(독과점 등), arms race, economics (since mid 1970). Critics argue that the situations explained by GT can be explained by conventional economic theories and there are 100 years old examples. However, GT (especially NE) can provide a general(unified) theory to all these phenomena in politics, economy and culture. That is why GT is good. 49/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (2) Empirical Proofs (cont’d) ã ã ã Verification using Statistics The 2 nd approach to empirical proof is statistical. In GT, it is assumed that NE exist in general. Using estimated equations from actual data, such assumption is verified. This approach deepens our understanding on how competition are proceeded and settled better than conventional economic theory, which assumes demand-supply estimation and price formation under perfect competition. However, more sophisticated mathematics and methodology are needed to build models with enough predictive power for the fields of politics and industry. 50/63

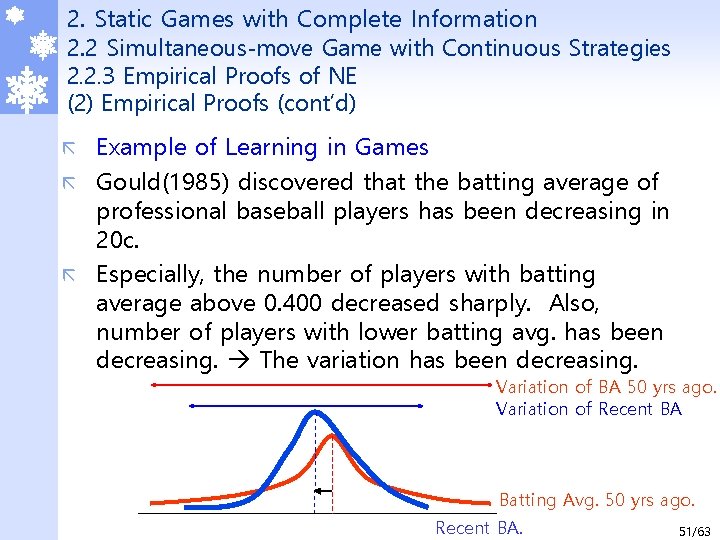
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (2) Empirical Proofs (cont’d) Example of Learning in Games ã Gould(1985) discovered that the batting average of professional baseball players has been decreasing in 20 c. ã Especially, the number of players with batting average above 0. 400 decreased sharply. Also, number of players with lower batting avg. has been decreasing. The variation has been decreasing. ã Variation of BA 50 yrs ago. Variation of Recent BA Batting Avg. 50 yrs ago. Recent BA. 51/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (2) Empirical Proofs (cont’d) ã Example of Learning in Games (cont’d) Gould(1985) calls this kinds of phenomena as standardization(표준화) or stabilization(안정화) effect. ã That is, when baseball game is introduced first back in early 20 c, positioning of defenders, pitching, batting methods were not optimized. Thus, extreme results(perfect game; no reaches to base for 9 innings, home-runs) emerged frequently. However, in present games, beating the opponents by a large margin or scoring big got difficult due to optimized plays from exercise and learning. ã Amateur baseball teams score bigger than professional teams. Ex) 동네축구 vs. 프로축구 ã 52/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (2) Empirical Proofs (cont’d) ã Example of Learning in Games (cont’d) ã In soccer games, the same thing’s happening. ã Even 10 years ago, Korean was not a match to European or South American teams. ã But after Hiddink’s coaching, Korea can beat Germany 3 -0 due to introduction of world class training and strategies. ã The fact that there isn’t too big a gap between European and South American teams’ scores is another proof. ã Same in electronics market. Quite until recently, Made in USA or Japan were the best. But nowadays, Made in Thailand or China are as good as theirs. No big difference. Choi, Hong-Man? No match first. But now? 53/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 3 Empirical Proofs of NE (2) Empirical Proofs (cont’d) ã Example of Learning in Games (cont’d) ã That is, if the game is frequently played and the rules of the game and conditions are stable and players are drafted from a stable group (no 3 m alien center in basketball), NE will be very plausible equilibrium concept. ã If the game is new, it could result in not-NE. But even in these cases, NE needs to be considered to check for its plausibility. ã If NE is not plausible, we need to figure out whynot? In most such cases, you will find that the reason was not NE but lack of understanding for the game. 54/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE ã ã ã Other than the practical-empirical criticisms, there are theoretical criticisms. For some of them, it is defensible. For others, defense is difficult to give clear answers. This is because GT is not a settled science. There are many rooms to study and grow : A totally settled science would be a dead science. Thus, GT is a live science. Myerson : In answering to the question, “Why would players in a game play the game to reach NE? ”, he asked “why not? ” Tell him a better answer than NE if you have one. 55/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Dealing with risk in NE ã Some say that players prefer safer strategies and this may lead to the outcome other than NE. ã Ex) NE in the below game is (A, A)(click). But Column may prefer ‘C’ because doing so guarantees (risk-averse) the payoff of 2 for Column. If Row has the same rationale, Row may choose ‘C’, in which case Column ends up with ‘ 0’ when Row chooses A (NE). Thus, it is safer for both to choose (C, C). Is this plausible? NO. ã Column Row A B C A 2, 2 3, 1 0, 2 B 1, 3 2, 2 3, 2 C 2, 0 2, 3 2, 2 56/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Dealing with risk in NE (cont’d) ã In response to the argument before, Morgan takes the following example. If Row really believes that Column will choose C, Row should take B. If Column knows this (Row will choose B), Column should choose A. If Row believes this, Row should take A or C If Row chooses A, it is the NE. If Row chooses C Column B Row A Column A or C If Column A, NE, If C, Row B… No equilibrium. ã Column Row A B C A 2, 2 3, 1 0, 2 B 1, 3 2, 2 3, 2 C 2, 0 2, 3 2, 2 57/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Multiple NE ã If there are many equilibria, prediction of unique outcome of the game fails. What good is the prediction if there are many possibilities? ã However, you can add more conditions to find a single equilibrium (prediction). In many previous examples, we saw that games with multiple equilibria becomes games with unique equilibrium when there exist ‘focal points. ’ ã Ex: The game of writing the same amount of money to get rewards (Divide 2000 KRW into 2 so that the summation should be 2000 KRW). NE? There are infinitely many NEs. (x, 2000 - x), where 0≤ x ≤ 2000. ã 58/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Multiple NE (cont’d) ã In practice, 50: 50 emerges as a focal point. the idea of equality-fairness is imprinted in people’s mind and works like an instinct. ã For this to be a focal point, this not only has to be apparent to each player but also has to be a common knowledge: What I know is known to others and this fact is known to others… and so on. ã For example, a western minded woman for equal gender might think 50: 50 division is a common knowledge. But conservative male chauvinist in middle-east might think he deserve 3 times more than women. no reward what so ever. ã 59/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Multiple NE (cont’d) ã The existence of the focal point is rather random in general. Thus, forming a focal point when there isn’t any, is closer to an art, that requires insight for history and culture. It is not a simple mathematic skill. ã Many game theorists might feel anxiety because this can’t be defined clearly by mathematics. But the context of game in history-culture is as important as mathematics. ã Even so, this aspect of mathematical ambiguity helps to find an unique equilibrium. ã 60/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Multiple NE (cont’d) ã The process of excluding irrational outcomes of the game in any sense is called ‘refinements (정련(精鍊); 정화, 순화). ’ ã The motives of refinement are different in games. It depends on how different players update their information on what choices they are making. ã In fact, the refinements of equilibria can be rational depending on the context of the game and narrow down the multiple equilibria into unique or small number of equilibria. ã 61/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Multiple NE (cont’d) ã Opposite case is there is no NE at all. Ex) Rock. Paper-Scissors. No NE in pure strategy ã However, this can be resolved by introducing the mixed strategy (choosing strategy randomly) in the next section. That is, there is always an equilibrium in mixed strategy games. Ex) Both Playing Rock 1/3, Paper 1/3, Scissors 1/3 is the NE. Pure strategy games are special cases of mixed strategy games. ã Of course, in very special cases, there does not exist any equilibrium even with mixed strategies. However, these cases are extremely exceptional, which can be dealt with in advanced theory. ã 62/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) ã Rationality Assumption for NE NE can be loosely stated that 1) system of strategies for each player or 2) system of players’ belief on other players’ choices. ã Thus, in NE, 1) a strategy that brings the best payoff will be selected under the belief on other players’ choice 2) each player’s belief on other players’ choice should be correct; players should act as believed. Þ This is called the mutual consistency of individual rationality. *Predictability and social relationship; No one will make friend with someone inconsistent in their actions. ã 63/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Rationality Assumption for NE (cont’d) (skip) ã For example, consider the next game. NE is (R 2, C 2) and the payoff is (3, 3). Row takes R 2 because s/he believes Column takes C 2. why? Because Row believes Column is rational. Same for Column; column believes Row is rational to take R 2. The beliefs need to be credible. ã End of Chapter 2 -2 Column Row C 1 C 2 C 3 R 1 0, 7 2, 5 7, 0 R 2 5, 2 3, 3 5, 2 R 3 7, 0 2, 5 0, 7 64/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) Rationality Assumption for NE (cont’d) (skip) ã The problem is that this belief lasts just once. For example, if Row believes [that Column believes [that Row takes R 3]], (click) Row gets to believe Column wrong takes C 3. (click) Thus, Row takes R 1. (click)-> belief (no reason to Column takes C 1 chain of belief is gained and all believe the links in the chain are rational. But these are not this) correct beliefs. ã Column Row C 1 C 2 C 3 R 1 0, 7 2, 5 7, 0 R 2 5, 2 3, 3 5, 2 R 3 7, 0 2, 5 0, 7 65/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 4. Theoretical Criticisms on NE (cont’d) ã Rationality Assumption for NE (cont’d) (skip) Thus, rationality alone, without correct belief, can not justify NE. ã Thus, we need to think deeper on meaning of the players’ common knowledge on rationality itself. (next section 2. 2. 5) ã 66/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (skip) What are the strategic choices that can be justified with rationality alone? As seen before, any combination of strategic choices can be an equilibrium. Is this general? NO. Very special. ã For example, dominated strategies can be excluded. Is there any other way? YES. A stronger concept than exclusion of dominated strategies can be used. ã One of them is ‘never a best response. ’ The strategy that survives the exclusion of ‘never a best response’ is called ‘rationalizable’ strategy. ã This concept is called ‘rationalizability. ’ ã 67/63

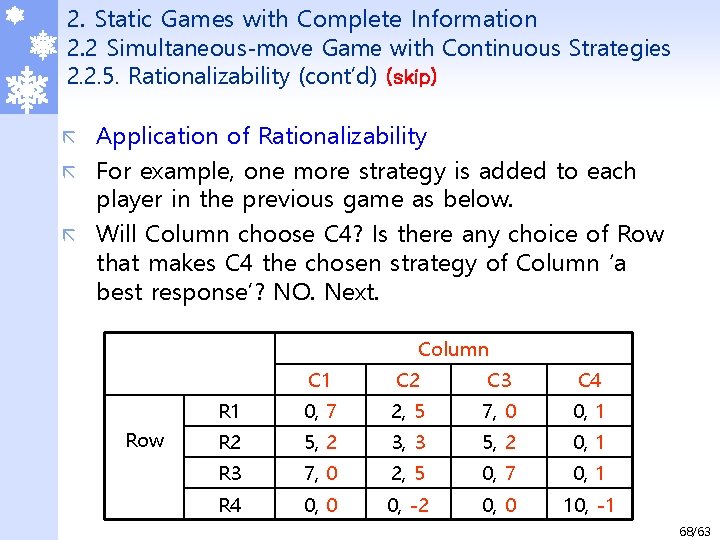
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) Application of Rationalizability ã For example, one more strategy is added to each player in the previous game as below. ã Will Column choose C 4? Is there any choice of Row that makes C 4 the chosen strategy of Column ‘a best response’? NO. Next. ã Column Row C 1 C 2 C 3 C 4 R 1 0, 7 2, 5 7, 0 0, 1 R 2 5, 2 3, 3 5, 2 0, 1 R 3 7, 0 2, 5 0, 7 0, 1 R 4 0, 0 0, -2 0, 0 10, -1 68/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) Application of Rationalizability (cont’d) ã If Column believes that Row will choose R 1, Column chooses C 1. If Row is believed to choose. R 2, Column chooses C 2. If R 3 C 3. If R 4 C 1 and C 3 are not differentiated as the best response. Thus, C 4 is ‘never a best response. ’ ã Thus, Row believes that Column will not choose C 4. ã Column Row C 1 C 2 C 3 C 4 R 1 0, 7 2, 5 7, 0 0, 1 R 2 5, 2 3, 3 5, 2 0, 1 R 3 7, 0 2, 5 0, 7 0, 1 R 4 0, 0 0, -2 0, 0 10, -1 69/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies Never a best Response 2. 2. 5. Rationalizability (cont’d) (skip) Dominated Strategy Application of Rationalizability (cont’d) ã Please remind that C 4 is ‘never a best response’ but is not inferior to C 1, C 2, and C 3. If C 4 was a dominated strategy, it couldn’t be the best response. ã dominated strategy ‘Never a Best Response(NBR). ’ But the other way is not always true. Never a Best Response is a more general concept. ã Column Row C 1 C 2 C 3 C 4 R 1 0, 7 2, 5 7, 0 0, 1 R 2 5, 2 3, 3 5, 2 0, 1 R 3 7, 0 2, 5 0, 7 0, 1 R 4 0, 0 0, -2 0, 0 10, -1 70/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã Application of Rationalizability (cont’d) ã That is, You Human (O). Human You (X). Then, Human ⊃ You. Thus, ‘NBR’ can be possible even when deletion of dominated strategy is not possible. Thus, the possibility of finding an equilibrium is more plausible with deletion of ‘NBR’ than with deletion of dominated strategy Deletion of NBR not only deletes dominated strategies but also other possibilities. As the repeated deletion of dominated strategies, NBR can be repeatedly deleted. ã ã 71/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã Application of Rationalizability (cont’d) ã Rational Row can delete C 4 and Column can delete R 4 because they are NBR. (C 1 R 3, C 2 R 2, C 3 R 1. Thus, R 4 will not be chosen. ) Column Rationalizable Outcome Row C 1 C 2 C 3 C 4 R 1 0, 7 2, 5 7, 0 0, 1 R 2 5, 2 3, 3 5, 2 0, 1 R 3 7, 0 2, 5 0, 7 0, 1 R 4 0, 0 0, -2 0, 0 10, -1 • If a game has NE, it is rationalizable. But even when there is no NE, the game may have rationalizable outcome. Next. 72/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã Application of Rationalizability (cont’d) In the game below, there is no NE but 4 outcomes are all rationalizable. . ã That is, 4 outcomes are to be selected in turn on the chain of beliefs. ã Thus, Rationalizability can provide the outcome when there is no NE. Also, rationalizability alone can narrow the range of possible equilibria. ã Column Row Rationalizable Outcome C 1 C 3 R 1 0, 7 7, 0 R 3 7, 0 0, 7 73/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã NE and Rationalizability In some games, deletions of NBR using rationalizability can lead to NE. In these cases, rationalizability reinforces NE. ã This kinds of games are especially important in economics. For example, this can be applied to the case where several companies are aware that the price is decided by the total amount of their production. ã Next example. ã 74/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã NE and Rationalizability (cont’d) Assume a small fishing village with no cold chain. In the morning, two boats sell the fish they caught last night. Fish should be sold and consumed in one day. There is no limit in catching. However, the two captains are aware that if the total catch is too big, the price will go down. ã The amount of catch by A is represented as X, and the catch by B is Y. The price, P, is decided by the following equation. P = 60 – (X + Y) ã 75/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) NE and Rationalizability (cont’d) ã The costs of catch are different depending on catch techniques. 30/unit for A and 36/unit for B. Thus, ã A’s profit; U=[(60 -X-Y)-30]X=(30 -Y)X-X 2 ã B’s profit; V=[(60 -X-Y)-36]Y=(24 -X)Y-Y 2 ã A and B need to react to each other’s catch to maximize their profits. differentiate and get BR functions!! ã Diff. U w. r. t. X => 30 -Y-2 X=0 => X=15 -0. 5 Y (A’s BR) ã Diff. V w. r. t. Y => 24 -X-2 Y=0 => Y=12 -0. 5 X (B’s BR) ã In a figure, next slide. ã 76/63

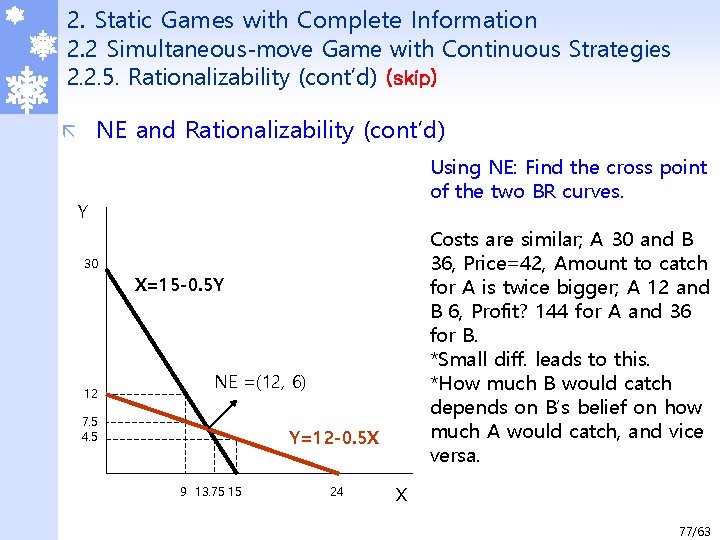
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) NE and Rationalizability (cont’d) ã Using NE: Find the cross point of the two BR curves. Y Costs are similar; A 30 and B 36, Price=42, Amount to catch for A is twice bigger; A 12 and B 6, Profit? 144 for A and 36 for B. *Small diff. leads to this. *How much B would catch depends on B’s belief on how much A would catch, and vice versa. 30 X=15 -0. 5 Y 12 NE =(12, 6) 7. 5 4. 5 Y=12 -0. 5 X 9 13. 75 15 24 X 77/63

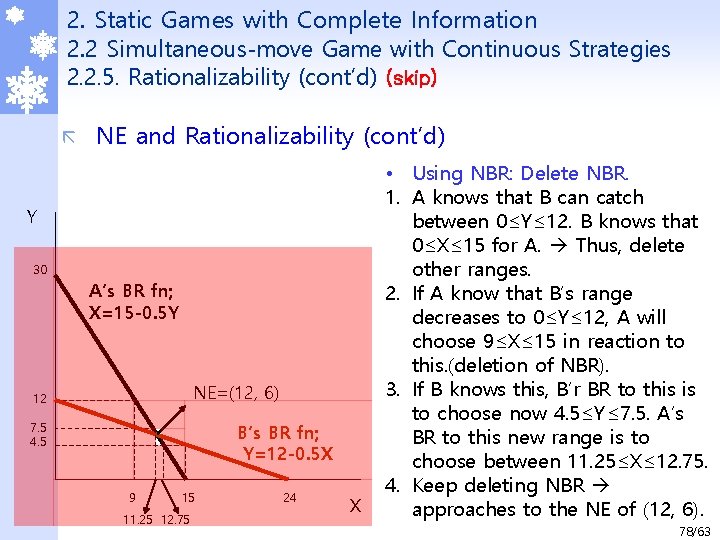
2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã NE and Rationalizability (cont’d) Y 30 A’s BR fn; X=15 -0. 5 Y NE=(12, 6) 12 7. 5 4. 5 B’s BR fn; Y=12 -0. 5 X 9 15 11. 25 12. 75 24 X • Using NBR: Delete NBR. 1. A knows that B can catch between 0≤Y≤ 12. B knows that 0≤X≤ 15 for A. Thus, delete other ranges. 2. If A know that B’s range decreases to 0≤Y≤ 12, A will choose 9≤X≤ 15 in reaction to this. (deletion of NBR). 3. If B knows this, B’r BR to this is to choose now 4. 5≤Y≤ 7. 5. A’s BR to this new range is to choose between 11. 25≤X≤ 12. 75. 4. Keep deleting NBR approaches to the NE of (12, 6). 78/63

2. Static Games with Complete Information 2. 2 Simultaneous-move Game with Continuous Strategies 2. 2. 5. Rationalizability (cont’d) (skip) ã NE and Rationalizability (cont’d) • Using BR? 1. Start at any point. Ex) Start at X=18. 2. B’s BR to X=18 Y=3 3. A’s BR to this X=13. 5 4. B’s BR to this Y=5. 25. . approaches to NE; same result! Y 30 A’s BR fn; X=15 -0. 5 Y *Problem in application of BR in this case? This game is executed simultaneously, not sequentially as in BR method. 12 B’s BR fn; Y=12 -0. 5 X 5. 25 3 13. 5 15 18 24 X *Rationalizability is different. The strategy is chosen once simultaneously and explicitly. 79/63
 Complete details example
Complete details example Static games of complete information exercises
Static games of complete information exercises Describe katniss conflicted emotions about peeta
Describe katniss conflicted emotions about peeta Outdoor games and indoor games
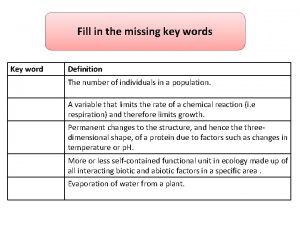
Outdoor games and indoor games Complete the missing word to complete the three key words
Complete the missing word to complete the three key words Complete subject and simple subject
Complete subject and simple subject Hidden information games
Hidden information games Extensive games with imperfect information
Extensive games with imperfect information Short questions
Short questions Complete the table with mahbubs information
Complete the table with mahbubs information Complete the table with mahbubs information
Complete the table with mahbubs information Incomplete vs imperfect information
Incomplete vs imperfect information Blockly games turtle
Blockly games turtle Target games examples
Target games examples Plokmijnuhbygvtfcrdxeszwaq used as an adjective
Plokmijnuhbygvtfcrdxeszwaq used as an adjective Wap games
Wap games Wandsworth school games
Wandsworth school games Types of games and sports
Types of games and sports Twoplayer games
Twoplayer games Twoplayer games
Twoplayer games Yout
Yout Tipp24 online games
Tipp24 online games Thesis statement about video games
Thesis statement about video games Olympic powerpoint template
Olympic powerpoint template Plato computer games
Plato computer games Abcde games
Abcde games The olympic games are an international sports festival
The olympic games are an international sports festival Java games programming
Java games programming Kumeyaay baskets
Kumeyaay baskets Swot analysis for gaming industry
Swot analysis for gaming industry Nuts and volts hunger games
Nuts and volts hunger games Settings in the hunger games
Settings in the hunger games Hunger games questions
Hunger games questions Hunger games inspired by greek mythology
Hunger games inspired by greek mythology What is the richest district in the hunger games
What is the richest district in the hunger games Tesserae hunger games
Tesserae hunger games Hunger games copyright
Hunger games copyright Suzanne marie collins
Suzanne marie collins Olympics purpose
Olympics purpose Us history staar eoc review
Us history staar eoc review What do finding nemo and robocop have in common
What do finding nemo and robocop have in common Terrence andrew davis
Terrence andrew davis Contrive experience
Contrive experience How has peeta managed to stay safe
How has peeta managed to stay safe Materi ownership kelas 6 sd
Materi ownership kelas 6 sd Biology staar kahoot
Biology staar kahoot Sports includes all forms of competitive activity or games
Sports includes all forms of competitive activity or games 3 types of sports
3 types of sports Serious games network
Serious games network Lama permainan sepak
Lama permainan sepak Selective mutism games
Selective mutism games Rhyme time answers
Rhyme time answers Scentsy games
Scentsy games Riot games organizational structure
Riot games organizational structure Mean median mode card game
Mean median mode card game Mulmuley games
Mulmuley games Sandra cruz denton tx
Sandra cruz denton tx Study island skateboard game
Study island skateboard game Python trinket 3
Python trinket 3 Dylan wiliam feedback
Dylan wiliam feedback Pride youth games
Pride youth games Minute to win it physics games
Minute to win it physics games Small basic code for games
Small basic code for games Www.atantot-extra.co.uk
Www.atantot-extra.co.uk Medical terminology jeopardy game
Medical terminology jeopardy game Text computer games
Text computer games Renpy extend
Renpy extend Picture theory wittgenstein
Picture theory wittgenstein Hunger games introduction paragraph
Hunger games introduction paragraph Live kahoot games
Live kahoot games The hunger games a hero's journey begins
The hunger games a hero's journey begins Cooperative pe games
Cooperative pe games Https //sites.google.com games
Https //sites.google.com games Wittgenstein language games
Wittgenstein language games Greenfoot programming
Greenfoot programming Abbreviation for interjection
Abbreviation for interjection Deterministic games examples
Deterministic games examples Mashup games
Mashup games Fcat explorer games
Fcat explorer games Waygook games
Waygook games